Heritability Estimation Approaches Utilizing Genome-Wide Data
Amit K. Srivastava, Amit K. Srivastava, Scott M. Williams, Scott M. Williams, Ge Zhang, Ge Zhang
Abstract
Prior to the development of genome-wide arrays and whole genome sequencing technologies, heritability estimation mainly relied on the study of related individuals. Over the past decade, various approaches have been developed to estimate SNP-based narrow-sense heritability (
Basic Protocol 1 : GREML (GCTA)
Alternate Protocol 1 : Stratified GREML
Basic Protocol 2 : LDAK
Alternate Protocol 2 : Stratified LDAK
Basic Protocol 3 : Threshold GREML
Basic Protocol 4 : LD score (LDSC) regression
Basic Protocol 5 : SumHer
INTRODUCTION
A long-standing question in quantitative and behavioral genetics is whether the variation in a particular trait is due to genetic or environmental factors (Visscher et al., 2008). A key step in finding an answer to this question is partitioning the observed phenotypic variance into variance components attributable to unobserved genetic and environmental factors. R. A. Fisher (Fisher, 1918) first modeled and partitioned the phenotypic variance into genetic and environmental components without any knowledge of specific genes affecting the trait (Visscher & Goddard, 2019). Although he did not use the term ‘heritability’, his research laid the foundation for various future approaches for the estimation of heritability (Falconer, 1960; Walsh, 1998).
Heritability is defined as the proportion of phenotypic variance that is attributable to genetic factors in a given population at a specific time(Falconer, 1960; Walsh, 1998). Heritability can be defined in two ways. The broad-sense heritability (H2) estimates the proportion of phenotypic variance attributable to all genetic factors, including additive genetic effects (A), dominant genetic effects (D), and epistatic effects (G × G) (Mayhew & Meyre, 2017; Visscher et al., 2008; Zhu & Zhou, 2020). In contrast, narrow-sense heritability (h2) estimates the proportion of phenotypic variance attributable to additive genetic effects (A) or breeding values (Mayhew & Meyre, 2017; Visscher et al., 2008; Zhu & Zhou, 2020). Since h2 is more relevant to the evaluation of genetic influence on phenotypic resemblance of relatives and predicting evolutionary responses to selection, it is a commonly used parameter for heritability estimation and applications (Visscher et al., 2008).
Heritability plays an important role in several areas of biology such as agriculture, medicine, and evolution (Visscher et al., 2008). It facilitates selective breeding programs to improve the quality of plant and domestic animals (Alvarez, 2017; Bernardo, 2020; Berry et al., 2003, 2014; Cassell, 2009; Manjula et al., 2018; Miglior et al., 2017; Palmquist & Jenkins, 2017; Utrera & Van Vleck, 2004; Velasco & Fernández-martínez, 2002). Heritability also provides insights into the genetic architecture of complex traits and diseases (Eichler et al., 2010; Friedman et al., 2021; Lunde et al., 2007; Manolio et al., 2009; Silventoinen et al., 2003; Tenesa & Haley, 2013; Vinkhuyzen et al., 2013; Visscher et al., 2007; Wray et al., 2007). For over a century, heritability has played a key role in measuring the genetic influence on various traits and diseases (Dempster & Lerner, 1950; Falconer, 1960, 1965). A large heritability implies that genetic factors have a strong influence on a trait or disease. Being an important parameter of genetic influence on phenotype, heritability has been frequently used as the basis for genetic linkage and genetic association studies (Boomsma et al., 2002; Friedman et al., 2021; Institute of Medicine, 2006). These studies led to the discovery of genes associated with various anthropometric and behavioral traits and diseases such as birth defects, psychiatric disorders, etc. (Institute of Medicine, 2006; Visscher et al., 2008). Therefore, an accurate estimation of heritability can help prioritize the use of resources for further genetic studies (Zhu & Zhou, 2020). Heritability acts as a key for understanding the evolution of quantitative traits and diseases (Bateson, 1922; Fisher, 1930; Grant & Grant, 1995; Hadfield, 2008; Kelly, 2011; Kingsolver et al., 2001; Lande & Arnold, 1983; Mousseau & Roff, 1987; Wood et al., 2016). Particularly, heritability determines how a population will respond to selection. Therefore it can be utilized to compare the evolution of a particular trait or disease across different populations at the same time and within a population at different timepoints (Mayhew & Meyre, 2017).
To date, aspects of heritability such as its conceptualization and applications (Powell et al., 2010; Visscher et al., 2008, 2010; Wray et al., 2013; Yang et al., 2017), assessments of missing heritability (Brookfield, 2013; Eichler et al., 2010; Genin, 2020; Golan et al., 2014; Manolio et al., 2009; Maroilley & Tarailo-Graovac, 2019; Tenesa & Haley, 2013; Yang et al., 2011; Zaitlen & Kraft, 2012), methods and approaches (Boomsma et al., 2002; Browning & Browning, 2012; Evans, Tahmasbi, Jones, et al., 2018; Friedman et al., 2021; Hall & Bush, 2016; Pasaniuc & Price, 2017; Powell et al., 2010; Speed & Balding, 2015; Speed et al., 2020; VanRaden, 2008; Weir et al., 2006; Yang, Manolio et al., 2013; Zaitlen & Kraft, 2012), statistical models for various data types (Zhang et al., 2021; Zhu & Zhou, 2020) have been addressed in many reviews. In particular, heritability estimation methods and approaches have been key to many of these reviews irrespective of their central theme. These approaches depend on either the expected genetic similarity in pedigrees, e.g., family-based approaches (Allison et al., 1996; Boomsma et al., 2002; Eaves et al., 1978; Falconer, 1960; Lunde et al., 2007; Nance et al., 1983; Stunkard et al., 1990; Walsh, 1998; Wright, 1921), or the realized genetic similarity among individuals in a population of mixed relationships—e.g., population-based approaches (Browning & Browning, 2012; Lee & van der Werf, 2006; Lee et al., 2010; Ritland, 1996, 2000; Thomas, 2005; VanRaden, 2008; Yang et al., 2010, 2014, 2017; Zhang et al., 2010). Population-based approaches generally utilize single nucleotide polymorphisms (SNPs) to estimate realized genetic similarity, and are usually called SNP-heritability estimation approaches (Speed et al., 2012; Tang et al., 2022; Tenesa & Haley, 2013; Yang, Lee, et al., 2011; Yang et al., 2014; Yang, Manolio, et al., 2011; Zhu & Zhou, 2020).
New approaches to estimate heritability (VanRaden, 2008; Yang et al., 2010) were developed in parallel with advanced genotyping and sequencing technologies (1000 Genomes Project Consortium et al., 2010, 2012, 2015; International HapMap, 2005) that facilitated the estimation of realized genetic similarity; these approaches became popular for estimating SNP-heritability in natural populations, as they did not require large pedigree recruitment. In the last decade, several approaches have been developed for estimation of SNP-heritability of complex human traits and diseases. These approaches utilize either individual-level genetic variations such as genome-wide complex trait analysis (GCTA; Yang et al., 2010; Yang, Lee, et al., 2011), linkage-disequilibrium-adjusted kinships (LDAK; Speed et al., 2012, 2017), threshold genome-based restricted maximum likelihood (Threshold GREML; Zaitlen et al., 2013), or summary results from GWAS such as LD Score (LDSC) regression (Bulik-Sullivan et al., 2015; Zaitlen et al., 2013) and SumHer (Speed & Balding, 2019) (Fig. 1). Recently, several studies compared SNP-heritability estimation approaches using simulated and empirical datasets (Evans, Tahmasbi, Vrieze, et al., 2018; Hou et al., 2019; Speed et al., 2017, 2020; Tang et al., 2022; Uricchio, 2020; Yang et al., 2017; Zhu & Zhou, 2020). However, few resources provide hands-on training for these various approaches, thereby warranting an overview along with step-by-step protocols for practical applications.
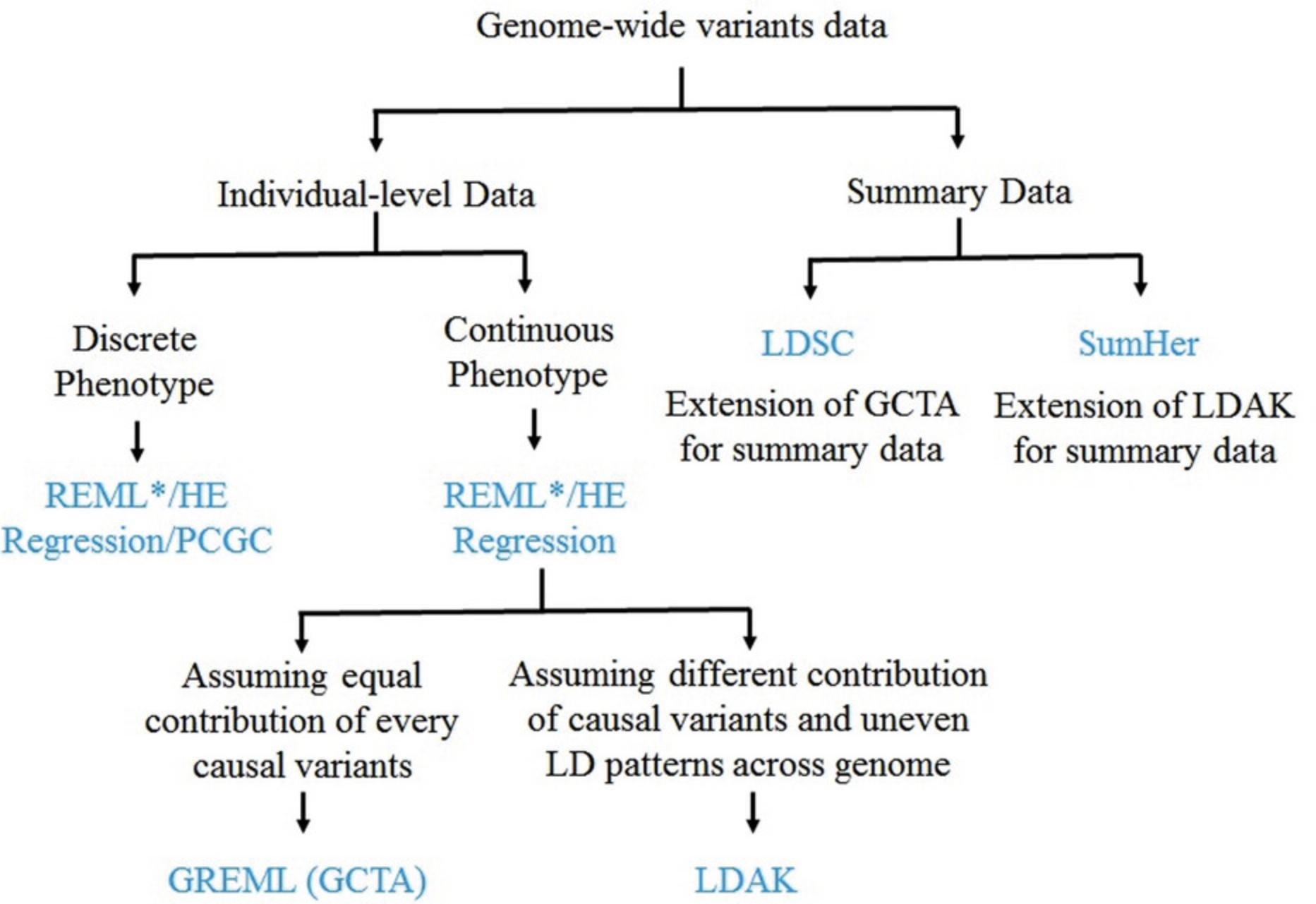
The current review provides an updated summary of SNP-heritability estimation approaches utilizing either individual-level genome-wide data or summary results from previous GWAS. These approaches utilize a variety of methods such as Maximum Likelihood (ML; Thompson, 1971; Visscher et al., 2006), Restricted Maximum Likelihood (REML; Lee & van der Werf, 2006; Yang et al., 2010), Haseman-Elston (HE) Regression (Haseman & Elston, 1972; Sham & Purcell, 2001), and Phenotype Correlation–Genotype Correlation (PCGC; Golan et al., 2014). REML is the most widely used method for individual-level genetic data, and is employed in linear mixed model (LMM) to simultaneously estimate the contribution of fixed and random effects. Therefore, we focus here on the REML methods while discussing the approaches developed for individual-level genetic data. Likewise, we discuss LDSC (Bulik-Sullivan et al., 2015), and SumHer (Speed & Balding, 2019) that utilize the regression method and REML, respectively, to estimate SNP-heritability from GWAS summary results. We discuss each heritability estimation approach in the context of statistical basis, utility, advantages, and limitations. We also provide stepwise protocols to apply commonly used approaches utilizing individual-level genetic data such as GCTA (Yang et al., 2010; Yang, Lee, et al., 2011), LDAK (Speed et al., 2012, 2017), and Threshold GREML (Zaitlen et al., 2013), as well as GWAS summary results such as LDSC (Bulik-Sullivan et al., 2015; Bulik-Sullivan et al., 2015), and SumHer (Speed & Balding, 2019). We present this review as a template to the researchers who need to estimate and use heritability in their research and as a reference to the geneticists who want to develop or extend heritability estimation approaches.
AN OVERVIEW OF SNP-HERITABILITY ESTIMATION APPROACHES
Genome-wide SNP arrays and whole genome sequencing technologies have revolutionized many aspects of human genetics such as determination of genetic susceptibility and underlying mechanisms that increase risk of diseases, estimation of heritability, and understanding the evolution of complex traits (Eichler et al., 2010; Visscher et al., 2008; Zaitlen & Kraft, 2012). Genome-wide association studies (GWAS) have discovered a multitude of genetic variants associated with various complex human traits and diseases (Buniello et al., 2019). However, variants derived from GWAS explain only a small proportion of phenotypic variance as compared to family studies, leading to a major question of missing (hidden) heritability (Manolio et al., 2009). There are several possible reasons for missing heritability, such as weak linkage disequilibrium (LD) between genotyped variants and ungenotyped causal variants, common variants with small effects that do not reach the canonical significance threshold (5 × 10–8) in GWAS, rare variants with large effects not captured by genotyping arrays, contribution of non-additive effects, gene–environmental interactions, and overestimation of narrow-sense heritability in pedigree-based studies due to shared environmental confounding (Eichler et al., 2010; Gibson, 2012; Manolio et al., 2009; Yang et al., 2017; Zhang, 2015). In last decade, several approaches have been developed that utilize genome-wide variations instead of only statistically significant variations to solve the problem of missing heritability of complex traits (Bulik-Sullivan et al., 2015; Speed & Balding, 2019; Speed et al., 2012, 2017; Yang, Lee, et al., 2011; Zaitlen et al., 2013). These approaches successfully explained a large proportion of phenotypic variance attributable to genome-wide SNPs for a variety of complex human traits and diseases. Unlike widely studied continuous traits such as anthropometric traits, behavioral traits, and pre- and perinatal traits, dichotomous traits such as diseases are represented on a discrete scale (e.g., 0-1). Therefore, observed heritability on a risk scale is usually parameterized on an unobserved continuous liability scale so that the heritability is independent of disease prevalence (Falconer, 1965; Lee et al., 2011; Tenesa & Haley, 2013; Yang et al., 2017). Here, we explain major advances in the approaches based on genome-wide SNP data at individual or summary level with their advantages and limitations (Table 1).
| Approach | Statistical assumptions | Description | Advantages | Limitations |
|---|---|---|---|---|
| GREML-SC | (i) Normal distribution of SNP effects $[{{\rm{u}}}_{\rm{i}} \sim {\rm{\ N(0,h}}_{\rm{g}}^2/{\rm{m}})]$, independent of LD and inversely proportional to MAF; (ii) Polygenic model; (iii) Uncorrelated genetic and environmental components. | (i) Each SNP contributes equally to phenotypic variance i.e., ${\rm{\sigma }}_i^2 = {\rm{h}}_{\rm{g}}^2/{\rm{m}}$; ii) ${\rm{\hat{h}}}_{{\rm{SNP}}}^2$ is dependent on the tagging of causal variants by the SNPs used to create the GRM. | First ever approach to estimate SNP-heritability using genome-wide data in unrelated individuals. | (i) Highly dependent on LD among assayed and causal variants and biased to the extent to which the average LD among causal variants differ from the average LD among SNPs used to create GRM. (ii) No flexibility of modeling uneven LD and MAF influence as compared to other contemporary approaches. |
| GREML-MS | Each GRM should follow same assumptions as GREML-SC. SNP effects follow the distribution |
(i) Multi-component GREML—multiple GRMs based on MAF bins are fitted simultaneously in the linear mixed model (LMM); (ii) GRMs based on variety of bins such as chromosomes, genomic regions, functional annotation can be used. | Creating GRMs based on MAF bins can address the influence of MAF on SNP effects and variance. Since LD depends on MAF, GREML-MS can resolve uneven tagging of causal variants up to some extent. | (i) Biased when LD structure of causal variants differ from that of the SNPs used to create the GRM; (ii) Relatively large standard errors. |
| GREML-LDMS-R | Same as GREML-MS. | Multi-component GREML that bins SNPs by their MAF and regional LD scores. | Same as GREML-MS with additional advantage due to LD bins. | (i) Similar to GREML-MS—if regional LD scores of causal variants differ from surrounding SNPs used to create GRM; (ii) Relatively large standard errors. |
| GREML-LDMS-I | Same as GREML-MS. | Multi-component GREML that bins SNPs by their MAF and individual LD scores. | To date, best version of GREML (least biased approach) which can address the uneven tagging of causal variants and the influence of MAF on SNP effects. | (i) Relatively large standard errors; (ii) Usually runs 20 genetic components, therefore, difficult to constrain REML (0 < ĥ2 < 1), particularly when ĥ2 and/or sample size is small. |
| LDAK |
Same as GREML-SC, except that (i) contribution of causal variants are different depending on their LD with surrounding SNPs. LDAK allows modeling of uneven LD patterns across genome via weighing thinned SNPs differently and the influence of MAF on SNP effects. |
Developed to address the problem of uneven tagging of causal variants by the SNPs used to create GRM. Recommends using α = −0.25. | Can correct uneven tagging of causal variants and allows modeling the influence of MAF on SNP effects. | (i) As biased as GREML-SC if assumptions aren't met; (ii) generally, larger standard errors as compared to GREML. |
| LDAK-MS | Each GRM must hold same assumptions as LDAK. | Multi-component version of LDAK that bins SNPs by MAF. | Developed to give flexibility of fitting various models based on MAF bins. | (i) Less biased than LDAK, but more biased than GREML-LDMS; (ii) Relatively large standard errors. |
| Threshold GREML | Estimates associated with the GRM without threshold are like GREML-SC. Variance attributable to the GRM with threshold represents ( |
Multi-component GREML with two GRMs: first GRM is created from all SNPs and second GRM is created by setting off-diagonals below a set threshold to 0. | Generally useful in samples with extended genealogy. | It can be upwardly biased by shared environmental influences. |
| LD score (LDSC) regression | Polygenic model with normally distributed SNP effects. Statistical assumptions are same as GREML |
Slope from regression of χ2 (from GWAS) on SNPs’ LD scores (from reference data) is used to estimate h2 attributable to the causal variants in LD with common SNPs present in GWAS summary result. | (i) As compared to GREML, it requires only summary results instead of individual-level data; (ii)Besides estimation of h2, LDSC can estimate genetic correlation with other traits; (iii) LDSC was further extended to estimate h2 attributable to various functional annotations, cell and tissue types (Finucane et al., 2015); (iv) Generally robust to confounding due to stratification and shared environmental effects; (v) computationally efficient. | (i) Estimated h2 is attributed to common causal variants only; (ii) Underestimates h2 if the trait is not highly polygenic; (iii) Biased estimates of h2 if reference population differs from the population used in GWAS. |
| SumHer | Basic idea is like LDSC with three differences: (i) SumHer models inflation as multiplicative whereas LDSC models as additive; (ii) Unlike LDSC, SumHer allows modeling uneven LD patterns across genome as well as influence of MAF on SNP effects; (iii) SumHer uses REML instead of regression to estimate SNP-heritability. | An extension of the LDAK model that can estimate h2 from summary results of previous GWAS. It can also partition h2g attributable to different annotations. | Multiplicative modeling of inflation can be useful to avoid overcorrecting confounding in large GWAS; (ii) SumHer has striking difference from LDSC in estimating h2 attributable to annotated regions. | Same as LDSC, except that SumHer apparently overestimates h2. |
- a Each approach is summarized on the basis of statistical assumptions and concept along with their advantages and limitations. ui, pi, wi, and $\sigma _i^2$ represent effect, MAF, weight and variance of SNP i, respectively; m represents number of SNPs used to create GRM or number of SNPs in summary statistics; s represents a subset of m present in a MAF bin, LD bin, genomic region or functional annotation; ${\rm{h}}_{\rm{g}}^2$ and ${\rm{h}}_{\rm{s}}^2$ represent SNP-heritability attributable to all SNPs used in the analysis and s subset of SNPs, respectively; α is a scaling factor, representing the influence of MAF on the variance of SNP effect.
Approaches Utilizing Individual-Level Genetic Data
The fundamental idea behind the approaches developed for individual-level genome-wide data is to estimate the realized genetic relationship among individuals by using genome-wide variants and using this relationship matrix to estimate the genetic variance. Yang et al. (2010) first utilized such approach to address the problem of missing heritability of human height. The study used 294,831 SNPs genotyped on 3925 unrelated individuals to calculate realized genetic relatedness and fitted this relatedness matrix in LMM to estimate SNP-based narrow-sense heritability (
Genome-wide Complex Trait Analysis (GCTA)
One of the most popular software packages for estimating SNP-heritability using genome-wide data from unrelated individuals is Genome-wide Complex Trait Analysis (GCTA), which uses a genome-based restricted maximum likelihood (GREML; Yang et al., 2010; Yang, Lee, et al., 2011) method. GCTA depends upon LD between genotyped variants and ungenotyped causal variants to estimate additive genetic variance in unrelated individuals.
The basic concept behind the method is to fit the effects of all the SNPs as random effects via an LMM. In this design, phenotype Y can be represented in simple equation form:
where A is GRM with each cell representing pair-wise genetic relatedness and I is identity matrix, assuming independence of environmental influence and no gene-gene or gene-environment interaction. For example, Ajk represents genetic relatedness between individuals j and k from m genotyped SNPs:
where pi is the minor allele frequency (MAF) and xi is the genotype code of the SNP i (xi = 0, 1, or 2).
A limitation of the GCTA approach is that it relies heavily on LD between assayed and causal variants (Speed et al., 2012; Zhu & Zhou, 2020). Therefore, it overestimates and underestimates the contribution of causal variants in high LD (strong LD between ungenotyped causal and genotyped variants) and low LD (weak LD between ungenotyped causal and genotyped variants) regions, respectively. In addition, genetic relatedness between a pair of individuals based on genotyped variants may not reflect genetic relatedness based on ungenotyped causal variants. If ungenotyped causal variants are in strong LD as compared to genotyped variants, heritability estimated using genotyped variants will be underestimated. GCTA suggests a uniform transformation of relatedness matrix [scaling the genotype matrix with 2p(1-p)–1, where p is MAF]. Such scaling implies that effect sizes are inversely proportional to MAF and each causal variant contributes equally to the phenotypic variance. However, equal contribution of each causal variant to the phenotypic variance is not realistic due to uneven LD patterns across the genome. Additionally, assortative mating, epistasis, and gene-environment interaction can bias heritability estimates by incorrectly allocating variance due to these phenomena to additive genetic effects. Likewise, population structure (admixed population) can bias the estimation of heritability. This bias can usually be avoided by identifying population structure through principal component analysis (PCA) and eliminating outliers from the data or correcting for admixed samples in the analysis by including the first few PCs as fixed effects in the LMM.
Later, several other variants of GCTA based on MAF stratified variants (GCTA-MS), LD and MAF stratified variants (GCTA-LDMS), were developed to overcome these limitations (see Alternate Protocol 1). These approaches facilitated not only partitioning of genetic variance into additive and non-additive components, but also variance attributed to different chromosomes, genes and inter-genic regions, biological pathways, and SNP functions (Yang et al., 2015; Yang, Manolio, et al., 2011). In addition, an approach was introduced to estimate SNP-heritability in individuals with close or extended relationships (Zaitlen et al., 2013). This approach essentially uses GREML with two GRMs; the first GRM is created using all SNPs, whereas a threshold is applied on the second GRM by setting off-diagonals < threshold to zero (see Basic Protocol 3). However, each approach has advantages and disadvantages (Table 1).
Linkage Disequilibrium Adjusted Kinships (LDAK)
Speed et al. (2012) developed a method (Linkage Disequilibrium Adjusted Kinships; LDAK) to overcome the bias arising from ungenotyped causal variants in regions of high or low LD. Yang and colleagues suggested a uniform scaling of the SNP-based kinship matrix [2p(1-p)–1, where p is MAF]. This transformation adjusts for the average bias caused by variable LD leading to uneven tagging of ungenotyped causal SNPs across the genome; however, it depends upon the MAF spectrum of the causal SNPs, which is generally not known. In contrast, LDAK suggests modification of the GRM according to local LD—contribution of the SNPs to the genetic similarity between a pair of individuals is weighted according to the LD with their neighboring SNPs. Estimating heritability using genetic similarity adjusted for local LD reduces the potential bias and increases the precision of the heritability estimate.
Reanalysis of the height data with LD-adjusted GRM showed a slight change in the estimated SNP-based heritability (
Like GCTA, LDAK estimates are highly sensitive to MAF of causal variants, population stratification, and SNP data type [arrays, imputed or Whole Genome Sequence (WGS)]. In addition, as LD is a function of MAF, the weighting strategy in LDAK can introduce MAF bias because it gives more weight to SNPs with lower MAF. An analysis using all SNPs from WGS data showed that LDAK weighted SNPs inversely proportional to their LD, which resulted in near-zero weights for common SNPs and very high weights for rare SNPs. This led to underestimated
Approaches Utilizing Summary Results From Previous GWAS
We discussed the approaches to estimate
LD Score (LDSC) regression
In GWAS, the deviation of observed χ2 test statistic for an SNP from its expected value under the null hypothesis (no association) is a function of LD between a target SNP and underlying causal variants (Yang et al., 2017). Therefore,
Like GCTA, LDSC has also been extended to estimate genetic correlation (rg) between traits using summary results. Genetic correlation can be defined as genetic covariance normalized by SNP-heritability [
A major advantage of LDSC is that it is faster than individual-based approaches and its computing time does not scale up with sample size. LDSC only requires summary data, which allows the reanalysis of summary data available from published meta-analyses. The LD score regression intercept can be used to estimate population stratification. Since summary results are available usually only for common variants, LDSC is limited in estimation of the variance explained by rare variants even with imputed or WGS data, and it is more sensitive to the genetic architecture of a trait. The estimates using LDSC depend on the LD scores and, thereby, the reference population in which LD scores were calculated. If there is a mismatch between the LD scores from the reference population and the target population used for GWAS, then LD score regression can be biased. A previous study showed that
LD score regression has been frequently applied to summary statistics from GWAS—to estimate the SNP-heritability of a trait, average bias due to confounding, heritability enrichments of SNP categories, and genetic correlation between a pair of traits. Like GCTA, LDSC also assumes that all causal variants contribute equally to the phenotypic variance, and therefore provides equal weight to each SNP. Although this model is widely used in statistical genetics, it usually underestimates the average
SumHer
Speed et al. (2019) proposed an approach (SumHer) to overcome the limitations of LDSC (Speed & Balding, 2019; Speed et al., 2020). The basic idea behind SumHer is that SNP heritability (e.g.,
SumHer proposes a solution to unequal contribution of
STEP-BY-STEP GUIDE FOR SNP-HERITABILITY ESTIMATION
Here, we provide a stepwise guide to estimate SNP-heritability using various approaches. For illustration purposes, we use individual-level genetic data and summary results from previous GWAS to estimate SNP-heritability of height and BMI. Individual-level genetic data from The Northern Finnish Birth Cohort (NFBC; 1966) consists of several metabolic trait measurements in 5402 individuals (Sabatti et al., 2009), genotyped for 364,580 SNPs using the Illumina HumanCNV370-Quadv3_C platform. Likewise, we use summary results from meta-analysis of height and BMI using UK Biobank and GIANT GWAS (2018) (Yengo et al., 2018).
The NFBC dataset is available through DbGaP authorized access. These data are for general research use—i.e., use of the data is limited only by the terms of the model Data Use Certification. There is no limitation in the usage of the genomic results outside the study for which they were originally consented. Summary results from the GIANT consortium are publicly available and can be accessed without restriction.
Although not an integral part of the protocol, we also provide a brief overview of widely used quality control procedure for phenotype and genotype data. Current approaches, developed for SNP-heritability estimation can also be used for various other purposes for example, estimation of genetic correlation, confounding due to population structure and cryptic relationship, gene enrichment analysis. However, we provide protocols only for the SNP-heritability estimation to align with the focus of the current review.
Resources
Before starting the estimation of SNP-heritability, it is necessary to install appropriate software; assemble the data files; input genotype (usually, plink format is preferred; if genotypes are present in variant call format (vcf) file, it can be converted to plink format for further analyses), phenotype (phenotype file should have at least three columns in the order family id, individual id, and phenotypic values), and summary results (usually contains an identifier/SNP id, effect allele, other allele, sample size, p value, and summary statistics); and download pre-calculated tagging (LD score) information from reference population (e.g., 1000 Genomes database, UK Biobank database). Reference population used for LD scores should be ancestrally similar to the GWAS samples. Similarly, we should be cautious while using summary results from previous GWAS and use the large studies with rigorous quality control.
Hardware
Any laptop/computer with 4 cores and 8-16 GB RAM is sufficient for most of the analyses in a reasonable time (Yang, Lee, et al., 2011).
Operating system
Linux-based operating system such as Ubuntu, Fedora etc.
Quality Control of Phenotype and Genotype Data
A detailed description of quality control for genome-wide analysis can be found elsewhere (Truong et al., 2022; Turner et al., 2011; Weale, 2010). Here, we briefly summarize the routinely used quality control procedures. In general, quality control of phenotypes depends on the research question, trait type (discrete or continuous), and other phenotypes/covariates available in the dataset. R (R Team, 2020)/R-Studio (R Team, 2019) (https://www.R-project.org) is a well-established platform for phenotype quality control. The first step is to select a key phenotype in a given dataset with multiple phenotypes, followed by summarizing the data. A density plot for continuous traits and bar plot for discrete traits can provide a rough idea about phenotype distribution and outliers. As normal distribution of variables is one of the assumptions in commonly used analyses, removing outliers (mean ±4*S.D.) is a common practice to attain normality in the dataset. However, one should be cautious while removing outliers and should choose this option only when alternative approaches such as data transformation (log or exponential) or adjusting with other covariates do not work. Phenotype data can be supplied to linear models either adjusted for the covariates or without adjusting for covariates where covariates can be supplied separately into the model.
Quality control of the genotype file is performed based on individuals and markers. PLINK (Chang et al., 2015; Purcell et al., 2007) (https://www.cog-genomics.org/plink/1.9) and R/R-Studio (R Team, 2019; R Team, 2020) (https://www.R-project.org) are routinely used for genotype quality control and plotting various quality measures, respectively. In general, individuals are filtered on the basis of genotype missing rate, average heterozygosity (inbreeding), inconsistency between biological and reported sex, and Mendelian errors (if pedigree information is available). Similarly, markers are filtered on the basis of call rate, minor allele frequency (MAF), and Hardy-Weinberg equilibrium (HWE). In addition, heritability estimation methods assume a homogeneous population; therefore it is advisable to check for population stratification and remove outliers using principal component analysis (PCA) or multi-dimensional scaling (MDS) based on the set of markers in the genome that are independent.
We performed the quality control procedure for NFBC dataset as mentioned above. After careful examination of the density plot of height and BMI, 33 samples were removed from the analysis. Phenotypes were adjusted for sex before fitting into LMM. Similarly, genotype data were controlled for individual and marker quality. Individuals were examined and excluded on the basis of genotype missing rate >5%, average heterozygosity ± 4*S.D., and inconsistency between reported and biological sex, whereas SNPs were examined and excluded on the basis of call rate <95%, MAF <1%, and HWE with p < 1.0E-6. After genotype and phenotype quality control, 5348 individuals genotyped on 324,851 autosomal SNPs with available phenotype information remained for SNP-heritability estimation analyses.
Protocols
Assuming that genotype and phenotype files are pre-processed for quality control, we provide the protocols below to run SNP-heritability analyses using different heritability estimation approaches. We believe that these protocols will make it easy for readers to estimate SNP-heritability (
Basic Protocol 1: GREML (GCTA)
This GREML protocol can be broadly categorized into three steps—(1) create genetic relatedness matrix (GRM); (2) remove one of the cryptically related individual pairs; (3) run restricted maximum likelihood (REML). GCTA allows multi-threading that can be enabled by using the flag --thread-num or -threads.
Software and files needed for GREML
Software
- GCTA (Yang et al., 2010; Yang, Lee, et al., 2011; https://yanglab.westlake.edu.cn/software/gcta/#Download)
Data file
- The Northern Finland Birth Cohort (Sabatti et al., 2009; https://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?study_id=phs000276.v2.p1)
1.Create GRM using plink format files (test.bed, test.bim, and test.fam).
Depending upon the requirements of the analysis, GRMs can be created in different ways, such as by using only autosomes, using each chromosome separately, using the X chromosome alone, or using a subset of SNPs.
- aUsing autosomes only:
- gcta64 --bfile test --autosome --make-grm-bin --out test_grm --thread-num 4;
- bBased on each chromosome separately:
- gcta64 --bfile test --chr 1 --make-grm-bin --out test_grm_chr1 --thread-num 4;
- gcta64 --bfile test --chr 2 --make-grm-bin --out test_grm_chr2 --thread-num 4;
- . . .
- gcta64 --bfile test --chr 22 --make-grm-bin --out test_grm_chr22 --thread-num 4;
- cUsing X chromosome.
- gcta64 --bfile test --make-grm-xchr --out test_grm_xchr --thread-num 4;
- dCreate GRM with a subset of SNPs (test_snplist.txt —one SNP on a line)
- gcta64 --bfile test --extract test_snplist --make-grm-bin --out test_grm_subset --thread-
- num 4;
2.Remove one individual from each cryptically related pair using kinship coefficient cutoff (0.05):
- gcta64 --grm test_grm --grm-cutoff 0.05 --make-grm-bin ---out test_grm_0.05 --thread-num 4;
3.Run REML with kinship matrix (test_grm_0.05.grm.bin, test_grm_0.05.grm.N.bin, and test_grm_0.05.grm.id) and phenotype file (test.phen):
- gcta64 --grm test_grm_0.05 --pheno test.phen --reml --out test_greml --thread-num 4;
REML can also be run in various alternative ways such as using GRMs created by a subset of SNPs, using multiple GRMs, adjusting for covariates and using discrete outcomes e.g., case-control status in phenotype file:
-
Run REML using GRM created by a subset of SNPs (test_grm_subset.grm.bin,test_grm_subset.grm.N.bin, andtest_grm_subset.grm.id):gcta64 --grm test_grm_subset --keep test_grm_0.05.grm.id --pheno test.phen --reml --outtest_greml_subset --thread-num 4;
-
Run REML using multiple GRMs (grm_chrs.txtis a text file with list of GRM names—one GRM name on a line):gcta64 --mgrm grm_chrs.txt --pheno test.phen --reml --outtest_greml_chrs --thread-num 4;
-
Adjust for covariates (--covarand--qcovarfor discrete and continuous covariates, respectively):gcta64 --reml --grm test_grm_0.05 --pheno test.phen --covar sex.txt --qcovar PCs.txt --out test_greml_adj --thread-num 4;
sex.txtis a list of individuals’ sexes (discrete variable) andPCs.txtis a file with first 10-20 principal components (continuous variable). Similar to the phenotype files, covariate files also have the first two columns as family id and individual id followed by covariate columns.
-
Run REML for case control data(test_cc.phen—phenotype file with case-control information). Let us assume that the prevalence of the disease is 0.1 in the general population. The option--prevalenceis used to specify the disease prevalence and transformation of${\rm{\hat{h}}}_{{\rm{SNP}}}^2$from observed discrete (0-1) scale to unobserved continuous liability scale.gcta64 --reml --grm test_grm_0.05 --pheno test_cc.phen --prevalence 0.1 --outtest_greml_cc --thread-num 4;
Alternate Protocol 1: STRATIFIED GREML
As seen in the previous example, SNP-heritability attributable to each chromosome can be estimated by simultaneously fitting GRMs based on each chromosome in to REML. Similarly, GREML can be run in various other stratified ways, for example, using GRMs created by a subset of SNPs stratified by either minor allele frequency (MAF) bins alone or both linkage disequilibrium (LD) and MAF bins. These variations of GREML were developed to adjust for the influence of MAF and local LD on the estimated SNP-heritability, and known as the GREML-MAF Stratified (GREML-MS) and GREML-LD and MAF Stratified (GEML-LDMS) approach, respectively. Like original GREML, stratified GREML is also performed in three major steps: (1) create GRM, (2) remove one of the cryptically related individual pairs, and (3) run REML. However, GREML-LDMS includes an additional step—calculation of LD scores (summation of r2 values between a SNP and all SNPs in a given genomic region) prior to creating GRMs. It is noteworthy that multiple GRMs are created and fitted in REML based on the stratification criteria in stratified GREML.
Software and files needed for Stratified-GREML
Software
- GCTA (Yang et al., 2010; Yang, Lee, et al., 2011)) (https://yanglab.westlake.edu.cn/software/gcta/#Download)
- R/R-Studio (R Team, 2019; R Team, 2020; https://www.R-project.org)
Data file
- The Northern Finland Birth Cohort (Sabatti et al., 2009; https://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?study_id=phs000276.v2.p1)
GREML-MS (Based on MAF bins only)
1a. Create GRMs:
- gcta64 --bfile test --autosome --maf 0.01 --max-maf 0.1 --make-grm-bin --out
- test_maf0.1_grm --thread-num 4;
- gcta64 --bfile test --autosome --maf 0.1 --max-maf 0.2 --make-grm-bin --out
- test_maf0.2_grm --thread-num 4;
- . . .
- gcta64 --bfile test --autosome --maf 0.4 --max-maf 0.5 --make-grm-bin --out
- test_maf0.5_grm --thread-num 4;
2a. Remove one of the cryptically related individual pairs: REML can be run with unrelated individuals by adding a flag --keep [list of individuals with kinship coefficient < threshold e.g. 0.05]. A list of individuals with kinship coefficient less than a set threshold can be created using the protocol provided in GCTA. Alternatively, the test_grm_0.05.grm.id file created in the GREML protocol can directly be used. It is noteworthy that stratified REML analysis is performed with multiple GRMs listed in a text file (one GRM name in a line).
3a. Run REML:
- gcta64 --mgrm greml_ms_grm_list.txt --pheno test.phen --reml --out test_greml_ms --thread-num 4;
GREML-LDMS (based on LD and MAF bins)
1b. Calculate LD scores:
LD scores are calculated using option --ld-score-region [window size]. GCTA uses default window size of 200 Kb with 100Kb overlapping regions between two segments:
- gcta64 --bfile test --autosome --ld-score-region 200 --out test_ld --thread-num 4;
Import the output of the above command (test_ld.score.ld) to R and create quartiles based on either ldscore_SNP or ldscore_region. Save SNPs corresponding to each quartile as test_ld_q*.txt, where * is 1/2/3/4. Different bins are created on the basis of LD score quartiles and MAF ranges. For example, SNPs within each MAF range such as 0.01 < MAF ≤ 0.1, 0.1 < MAF ≤ 0.2,, 0.2 < MAF ≤ 0.3,, 0.3 < MAF ≤ 0.4 and 0.4 < MAF ≤ 0.5 can be binned on the basis of quartiles of regional or SNP LD scores.
2b. Create GRM:
- for i in $(seq 1 4); do
- gcta64 --bfile test --autosome --extract test_ld_q${i}.txt --maf 0.01 --max-maf 0.1 --make-
- grm-bin --out test_q${i}_maf0.1_grm --thread-num 4;
- done;
- for i in $(seq 1 4); do
- gcta64 --bfile test --autosome --extract test_ld_q${i}.txt --maf 0.1 --max-maf 0.2 --make-
- grm-bin --out test_q${i}_maf0.2_grm --thread-num 4;
- done;
- . . .
- for i in $(seq 1 4); do
- gcta64 --bfile test --autosome --extract test_ld_q${i}.txt --maf 0.4 --max-maf 0.5 --make-
- grm-bin --out test_q${i}_maf0.5_grm --thread-num 4;
- done;
3b. Remove one of the cryptically related individual pairs: One individual from the cryptically related pairs can be removed using the command provided in the GCTA protocol. Alternatively, an already filtered list of unrelated individuals can be used as in GREML-MS.
4b. Run REML:
- gcta64 --mgrm greml_ldms_grm_list.txt --pheno test.phen --reml --out test_greml_ldms --thread-num 4;
Basic Protocol 2: LDAK
This LDAK protocol can be divided into five steps—(1) Thinning of SNPs; (2) calculating weights of thinned SNPs based on the pair-wise LD with all nearby SNPs in a bin (e.g., 100 kb); (3) creating kinship matrix; (4) removing one of the cryptically related individual pairs; (5) running REML. In the following protocols, we use a default setting of α = −0.25; the user may change this depending on the desired model. Like GCTA, LDAK also allows multi-threading for most of the analyses which can be enabled by using the option --max-threads.
Software and files needed for LDAK
Software
- LDAK (Speed et al., 2012, 2017) (http://dougspeed.com/downloads) for the first-time users and (http://dougspeed.com/downloads2) for the returning users
Data file
- The Northern Finland Birth Cohort (Sabatti et al., 2009; https://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?study_id=phs000276.v2.p1)
1.Thinning of SNPs:
Thinning of SNPs means removing one of the SNP pairs that are in strong LD with each other from the analysis. LDAK uses r2 = 0.98 and 100 Kb window size as default values:
- ldak5.1.linux --thin --bfile test --chr AUTO --window-prune .98 --window-kb 100;
- awk '{print $1, 1}' thin.in > weights.thin;
All thinned SNPs in the file weights.thin are assigned equal weight, i.e., 1, and are used for calculation of kinship matrix using LDAK-Thin model.
2.Calculate weights of thinned SNPs:
All the thinned SNPs are weighted equally for the LDAK-Thin model, whereas variant specific weights are calculated for the LDAK model. Prior to calculation of variant specific weights, LDAK cuts the thinned SNPs into multiple sections. We save these sections and corresponding SNP weights for each chromosome in a sub-directory ./sections/section${j}, where j represents chromosome number 1-22.
-
awk 'NR==FNR{x[
0; next} 1 ":" 4 ":" 5}' thin.in test.bim > extend_thin.in; -
awk 'NR==FNR{x[
0; next} 1 ":" 4 ":" 5}' thin.out test.bim > extend_thin.out; -
for j in $(seq 1 22); do
- mkdir -p ./sections/sections$j/;
- awk -v var=
1, a, ":"); if(a[1] == var) print a[2]}' extend_thin.in > - ./sections/sections$j/thin.in;
-
done;
-
for j in $(seq 1 22); do
- awk -v var=
1, a, ":"); if(a[1] == var) print a[2]}' extend_thin.out > - ./sections/sections$j/thin.out;
- awk -v var=
-
done
-
for j in $(seq 1 22); do
- ldak5.1.linux --cut-weights ./sections/sections
j --no-thin DONE -- - max-threads 4;
- ldak5.1.linux --calc-weights-all ./sections/sections
j --max-threads - 4;
- ldak5.1.linux --cut-weights ./sections/sections
-
done;
-
cat ./sections/sections{1..22}/weights.short > ./sections/weights.short;
Thinned SNPs in the file weights.short have SNP-specific weights and are used to calculate kinship matrix using the LDAK model. weights.short usually has a smaller number of SNPs than initially thinned SNPs because many of the thinned SNPs have zero weight and are not included in the calculation of kinship matrix.
3.Create kinship matrix.
- a.Calculate Kinship matrix using same weight for all thinned SNPs (LDAK-Thin model):
- ldak5.1.linux --calc-kins-direct test_grm_ldak_thin --bfile test --chr AUTO --weights
- weights.thin --power -0.25 --max-threads 4;
- b.Calculate Kinship matrix using SNP specific weights (LDAK Model):
- ldak5.1.linux --calc-kins-direct test_grm_ldak --bfile test --chr AUTO --weights
- ./sections/weights.short --power -0.25 --max-threads 4;
4.Remove one of the cryptically related individual pairs.
- a.LDAK-Thin model:
- ldak5.1.linux --filter test_ldak_thin_0.05 --grm test_grm_ldak_thin --max-rel 0.05 --max-
- threads 4;
- b.LDAK model:
- ldak5.1.linux --filter test_ldak_0.05 --grm test_grm_ldak --max-rel 0.05 --max-threads 4;
5.Run REML.
- a.LDAK-Thin model:
- ldak5.1.linux --reml test_ldak_thin --pheno test.phen --pheno --grm test_grm_ldak_thin --
- keep test_grm_0.05.grm.id --constrain YES --max-threads 4;
- b.LDAK model:
- ldak5.1.linux --reml test_ldak --pheno test.phen --pheno --grm test_grm_ldak --keep
- test_grm_0.05.grm.id --constrain YES --max-threads 4;
Alternate Protocol 2: STRATIFIED LADK
A stratified version of LDAK can be run using already calculated weights of thinned SNPs (see LDAK protocol). Unlike, GCTA, LDAK does not allow –min-maf or –max-maf option along with –calc-kins-direct. Therefore, markers based on MAF bins should be extracted from ‘test.bim’ files and the list should be used to extract the set of markers while creating kinship matrix (–extract list-of-SNPs.txt). Since, we are using pre-computed weights and advise one uses already pruned set of individuals (see LDAK protocol), we provide rest two steps here – i) create kinship matrix; ii) Run REML.
Software and files needed for Stratified LDAK
Software
- LDAK (Speed et al., 2012, 2017) (http://dougspeed.com/downloads) for the first-time users and (http://dougspeed.com/downloads2) for returning users
Data file
- The Northern Finland Birth Cohort (Sabatti et al., 2009; https://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?study_id=phs000276.v2.p1)
LDAK-Thin-MS model
1a. Create Kinship Matrix:
- ldak5.1.linux --calc-kins-direct test_maf0.1_ldak_thin_grm --bfile test --chr AUTO --
- extract test_maf0.1.txt --weights weights.thin --power -0.25 --max-threads 4;
- ldak5.1.linux --calc-kins-direct test_maf0.2_ldak_thin_grm --bfile test --chr AUTO --
- extract test_maf0.2.txt --weights weights.thin --power -0.25 --max-threads 4;
- . . .
- ldak5.1.linux --calc-kins-direct test_maf0.5_ldak_thin_grm --bfile test --chr AUTO --
- extract test_maf0.5.txt --weights weights.thin --power -0.25 --max-threads 4;
2a. Run REML:
- ldak5.1.linux --reml test_ldak_thin_ms --pheno test.phen --mgrm ldak_thin_ms_grm_list.txt
- --keep test_grm_0.05.grm.id --max-threads 4;
LDAK-MS Model
1b. Create Kinship Matrix:
- ldak5.1.linux --calc-kins-direct test_maf0.1_ldak_weights_grm --bfile test --chr AUTO --
- extract test_maf0.1.txt --weights ./sections/weights.short --power -0.25 --max-threads 4;
- ldak5.1.linux --calc-kins-direct test_maf0.2_ldak_weights_grm --bfile test --chr AUTO --
- extract test_maf0.2.txt --weights ./sections/weights.short --power -0.25 --max-threads 4;
- . . .
- ldak5.1.linux --calc-kins-direct test_maf0.5_ldak_weights_grm --bfile test --chr AUTO --
- extract test_maf0.5.txt --weights ./sections/weights.short --power -0.25 --max-threads 4;
2b. Run REML:
- ldak5.1.linux --reml test_ldak_ms --pheno test.phen --mgrm ldak_ms_grm_list.txt --keep
- test_grm_0.05.grm.id --max-threads 4;
Basic Protocol 3: THRESHOLD GREML
The threshold GRM approach uses two GRMs corresponding to one genetic component: a first GRM is the same as that created in GREML (without threshold) and a second GRM is created with a threshold by setting the off-diagonals that are <0.05 to 0. Here, we do not need to remove samples based on the GRM threshold. SNP-heritability attributable to the first kinship matrix is same as the SNP-heritability estimated by GREML. Overall, the estimate represents pedigree-based heritability, and h2 attributable to second GRM (
Software and files needed for Threshold GREML
Software
- GCTA (Yang et al., 2010; Yang, Lee, et al., 2011; https://yanglab.westlake.edu.cn/software/gcta/#Download)
Data file
- The Northern Finland Birth Cohort (Sabatti et al., 2009; https://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?study_id=phs000276.v2.p1)
1.Create GRM with threshold:
- gcta64 --grm test_grm --make-bK 0.05 --out test_grm_bK --thread-num 4;
2.Run Threshold GREML:
- gcta64 --mgrm threshold_grm_list.txt --reml --pheno test.phen --out test_Threshold --
- thread-num 4;
Basic Protocol 4: LD SCORE (LDSC) REGRESSION
LDSC allows
Software and files needed for LDSC Regression
Software
- LDSC (Bulik-Sullivan et al., 2015; Bulik-Sullivan et al., 2015; https://github.com/bulik/ldsc)
Data files
- Summary Results for height and BMI (Yengo et al., 2018; https://portals.broadinstitute.org/collaboration/giant/index.php/GIANT_consortium_data_files)
- LD Scores calculated in 1000 Genomes reference data (Bulik-Sullivan et al., 2015; https://alkesgroup.broadinstitute.org/LDSCORE)
1.Installation and activation.
LDSC can be installed from the resource provided earlier using following command:
- git clone https://github.com/bulik/ldsc.git;
LDSC is a python package and an Anaconda environment (environment.yml) present in the original package must be created before using LDSC. It installs a list python dependency for LDSC:
- conda env create --file environment.yml;
Before running LDSC an Anaconda environment is installed as above and must be activated as below:
- source activate ldsc
2.Download summary results.
The next step is to download the summary results that can be downloaded from the resource provided above directly or using command line via wget.
3.Convert to LDSC recognized format.
LDSC accepts a specific format of summary statistics with six columns—a unique identifier (rs id), allele 1 (effect allele), allele 2 (other allele), sample size, p -value and a signed summary-statistics (effect, odds ratio, log odds ratio, Z score). Sometimes sample size is not provided in the summary results. In that case, a uniform sample size can be provided by using a flag --N [sample size]. In the case of unsigned effects, LDSC assumes allele 1 to be a risk increasing/positively associated allele and processes summary result accordingly. Although summary results can be formatted manually, LDSC recommends using the python script munge_sumstats.py provided in the original package because it checks for several things besides converting summary result to LDSC format. In addition, it is recommended to use SNPs from summary results that are common in the HapMap3 dataset, particularly if the summary result is obtained from imputed data.
HapMap SNPs (w_hm3.snplist.bz2) can be downloaded from https://data.broadinstitute.org/alkesgroup/LDSCORE/ either directly or using command line via wget.
- Munge_sumstats.py --sumstats [summary-result] --out [sumstats-ldsc] --merge-alleles
- w_hm3.snplist.txt;
4.Estimate heritability.
To estimate heritability attributable to common variants present in summary result, χ2 values from the output of above command (sumstats-ldsc.gz) is regressed on the ld scores (sum of r2 values for a SNP with surrounding SNPs in a predefined window) calculated in a reference population such as the 1000 Genomes Project or UK Biobank. LD scores can be downloaded from the link provided in the resource. Assuming the GWAS included European population, LD scores should be used from European population, for example eur_w_ld_chr. In addition to LD scores, LDSC requires a regression weight file that includes r2 values for the SNPs used in the regression, i.e., GWAS SNPs. Generally, LDSC is not very sensitive to regression weights. Therefore, it is currently recommended to use the same LD scores for both flags. For partitioned h2 estimation, one may choose a subset of GWAS SNPs to calculate LD scores using 1000 Genomes data separately, and use them as regression weight.
- ldsc.py --h2 [sum-stats-file.gz] --ref-ld-chr eur_w_ld_chr/ --w-ld-chr eur_w_ld_chr/--out
- out_h2;
Basic Protocol 5: SumHer
SumHer is integrated into LDAK software; therefore, no extra software needs to be installed. Unlike LDSC, one must modify summary results to SumHer-compatible format manually. A compatible summary stats file has 5 or 6 columns (column names are case sensitive) with core columns: ‘Predictor’, ‘A1’, ‘A2’, ‘n’; then, there are three options to choose additional 1-2 columns. The last column could be ‘Z’, or last two columns could be ‘Direction’, ‘Stat’ or ‘Direction’, ‘P’. Predictor should be in ‘chr:position’ format.
Software and files needed for LDSC Regression
Software
- LDAK (Speed et al., 2012, 2017; http://dougspeed.com/downloads) for first-time users and (http://dougspeed.com/downloads2) for returning users
Data files
- Summary Results for height and BMI (Yengo et al., 2018; https://portals.broadinstitute.org/collaboration/giant/index.php/GIANT_consortium_data_files)
- LD Scores calculated in 2000 Great Britain samples from UK Biobank dataset; http://dougspeed.com/pre-computed-tagging-files)
- There are several tagging files available. Based on the recommendation of SumHer authors, we used BLD-LDAK tagging file (GBR population, HapMap SNPs) in our analysis.
1.Convert summary result to SumHer compatible format.
Let us assume height summary results were downloaded from GIANT consortium and unzipped to height_raw.txt using gunzip -c [summary-result.gz] > height_raw.txt. This file can be formatted to get height summary results with specific columns needed for SumHer.
- awk 'BEGIN{print "Predictor A1 A2 Direction P n"}
- (NR > 1 && (
2 == "C" || 2 == "T") - && (
3 == "C" || 3 == "T")){print 2, 5, 8}' - height_raw.txt > height.txt;
Then, download the list of HapMap3 SNPs with chromosome and position information (https://www.dropbox.com/s/xabjdu6squ6u56r/hapmap3.snps) and format the first column of height.txt:
- awk '(NR == FNR){a[
2; b[ 3 0}( 2$3 == - b[
3 1])){ 1]; print $0}' hapmap3.snps height.txt > height_hm3.txt;
2.Estimate heritability.
SNP tagging information must be downloaded prior to estimating heritability. LDAK has SNP tagging files pre-calculated using LDAK-Thin, BLD-LDAK, and BLD-LDAK-Light+Alpha models in different populations. These files can be downloaded from the link provided in the resource, depending on the population used in the original GWAS. It is noteworthy that alpha values should be downloaded from (https://www.dropbox.com/s/o7xphugm4mln9xa/pow.txt) for using BLD-LDAK-Light+Alpha model. This model is useful for gene enrichment analysis. Once SNP tagging information is downloaded, SNP-heritability can be estimated using the flag --sum-hers.
- ldak5.1.linux --sum-hers height --summary height_hm3.txt --tagfile
- bld.ldak.hapmap.gbr.tagging --check-sums NO;
- --Check-sums is a mandatory flag that tells the pipeline not to match the number of SNPs in summary result to those in the reference tagging file because, generally, all tag SNPs are not present in GWAS summary result.
ESTIMATION OF SNP-HERITABILITY USING INDIVIDUAL-LEVEL DATASET AND SUMMARY RESULTS
We compared eleven approaches for the estimation of SNP-heritability of height and BMI utilizing individual-level dataset (NFBC) and summary results from the GIANT consortium (Table 1). Using GREML, LDAK, and Threshold GREML approaches, we observed that genome-wide variations explained 56.9%-61.8% and 25%-28.1%variance in height and BMI respectively, in NFBC (Fig. 2, Table 2). We also used stratified analysis such as stratified-GREML and stratified-LDAK to estimate SNP-heritability attributable to different MAF and LD bins in NFBC. The sum of the heritability attributable to different bins was consistent with the results using single GRM (Fig. 2; Table 2). Comparison of the results from stratified-GREML (GREML-LDMS-R and GREML-LDMS-I) and stratified-LDAK (LDAK-Thin-MS, LDAK-MS) showed that the variance attributable to different bins based on MAF and LD scores were similar in both stratified-GREML and stratified-LDAK approaches (Fig. 3; Table 3). Likewise, variances attributable to different MAF bins in GREML-MS were similar to those in GREML-LDMS-R and GREML-LDMS-I (Fig. 3; Table 3). As reported previously (Evans, Tahmasbi, Vrieze, et al., 2018; Speed & Balding, 2019; Yang et al., 2017), LDSC underestimated the SNP-heritability (Height:
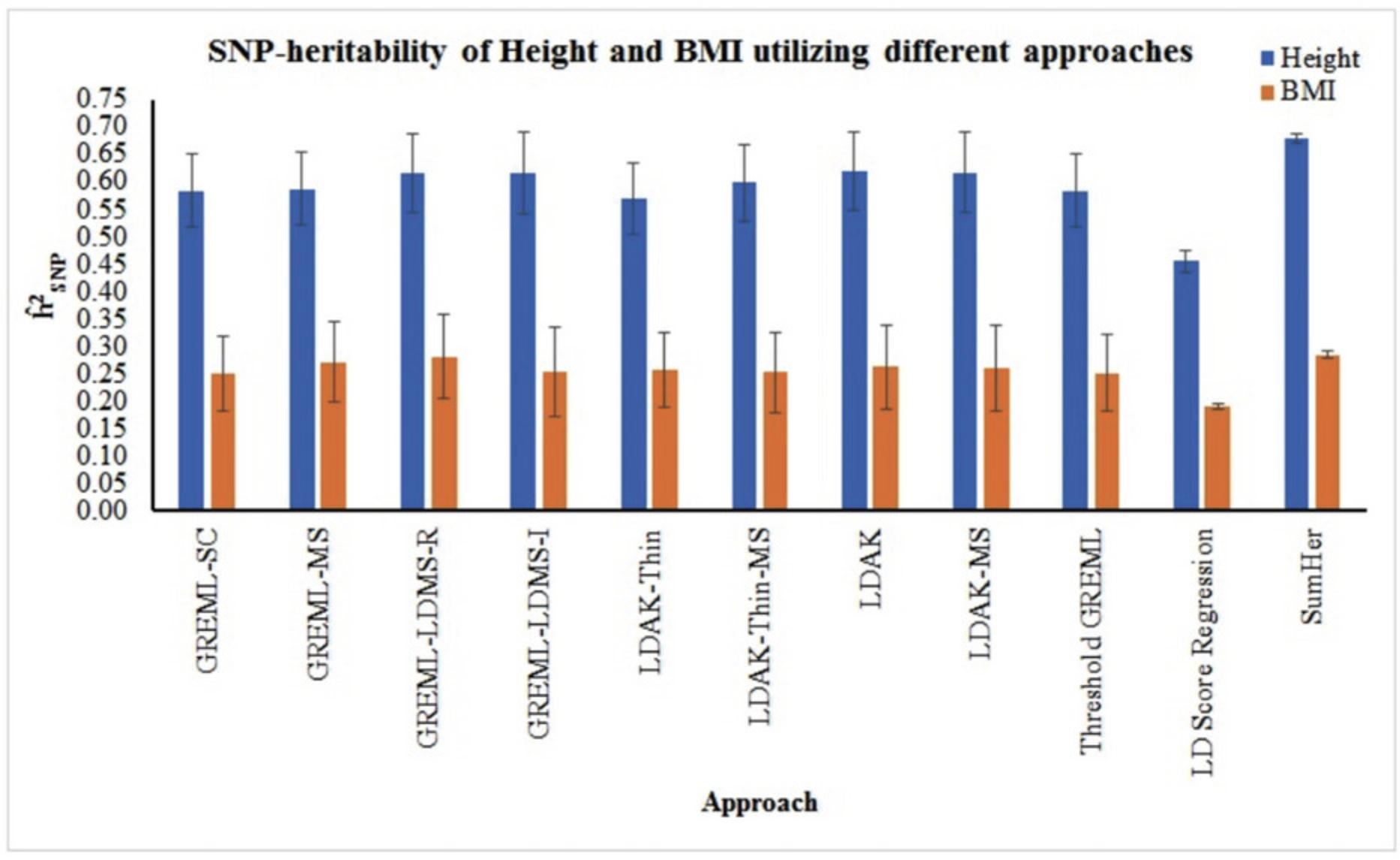
| Height (N = 3997) | BMI (N = 3985) | |||||
|---|---|---|---|---|---|---|
| Approach | ${\rm{\hat{h}}}_{{\rm{SNP}}}^2$ | S.E. | p-value | ${\rm{\hat{h}}}_{{\rm{SNP}}}^2$ | S.E. | p-value |
| GREML-SC | 0.5835 | 0.0658 | <1.11E-16 | 0.2494 | 0.0694 | 1.65E-04 |
| GREML-MS | 0.5867 | 0.0671 | <1.11E-16 | 0.2713 | 0.0719 | 8.06E-05 |
| GREML-LDMS-R | 0.6171 | 0.0719 | <1.11E-16 | 0.2811 | 0.0774 | 1.40E-04 |
| GREML-LDMS-I | 0.6152 | 0.0743 | <1.11E-16 | 0.2528 | 0.0811 | 9.13E-04 |
| LDAK-Thin | 0.5688 | 0.0647 | <1.11E-16 | 0.2571 | 0.0683 | 8.37E-05 |
| LDAK-Thin-MS | 0.5976 | 0.0684 | <1.11E-16 | 0.2527 | 0.0729 | 2.64E-04 |
| LDAK | 0.6183 | 0.0710 | <1.11E-16 | 0.2625 | 0.0761 | 2.81E-04 |
| LDAK-MS | 0.6173 | 0.0725 | <1.11E-16 | 0.2599 | 0.0781 | 4.38E-04 |
| Threshold GRMs | 0.5836 | 0.0656 | <1.11E-16 | 0.2509 | 0.0695 | 1.53E-04 |
| LD Score Regression | 0.4552 | 0.0193 | <1.11E-16 | 0.1908 | 0.0053 | <1.11E-16 |
| SumHer | 0.6785 | 0.0077 | <1.11E-16 | 0.2844 | 0.0078 | <1.11E-16 |
- a N represents the number of samples used for the analyses; GREML-SC, GREML-MS, GREML-LDMS-R, GREML-LDMS-I, LDAK-Thin-MS and LDAK-MS represent single component GREML, MAF stratified GREML, regional LD scores and MAF stratified GREML, Individual SNP LD score and MAF stratified GREML, MAF stratified LDAK-Thin model and MAF stratified LDAK model respectively. p-values were calculated using one sided z test.
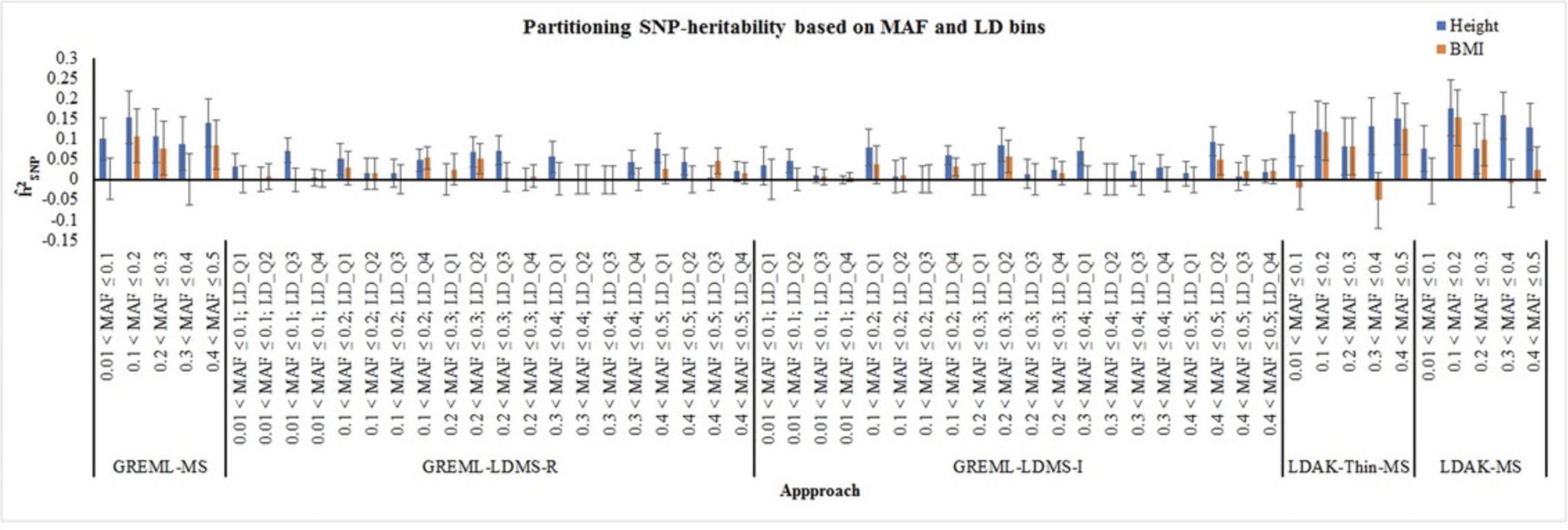
| Height | BMI | ||||||
|---|---|---|---|---|---|---|---|
| Approach | Bins | ${\rm{\hat{h}}}_{{\rm{SNP}}}^2$ | S.E. | p-value | ${\rm{\hat{h}}}_{{\rm{SNP}}}^2$ | S.E. | p-value |
| GREML-MS | 0.01 < MAF ≤ 0.1 | 0.0999 | 0.0531 | 2.99E-02 | 0.0021 | 0.0513 | 4.84E-01 |
| 0.1 < MAF ≤ 0.2 | 0.1531 | 0.0656 | 9.81E-03 | 0.1076 | 0.0663 | 5.24E-02 | |
| 0.2 < MAF ≤ 0.3 | 0.1075 | 0.0655 | 5.03E-02 | 0.0766 | 0.0664 | 1.25E-01 | |
| 0.3 < MAF ≤ 0.4 | 0.0878 | 0.0665 | 9.33E-02 | 0.0000 | 0.0646 | 5.00E-01 | |
| 0.4 < MAF ≤ 0.5 | 0.1383 | 0.0594 | 9.94E-03 | 0.0851 | 0.0601 | 7.85E-02 | |
| GREML-LDMS-R | 0.01 < MAF ≤ 0.1; LD_Q1 | 0.0324 | 0.0312 | 1.50E-01 | 0.0000 | 0.0322 | 5.00E-01 |
| 0.01 < MAF ≤ 0.1; LD_Q2 | 0.0000 | 0.0305 | 5.00E-01 | 0.0079 | 0.0312 | 4.00E-01 | |
| 0.01 < MAF ≤ 0.1; LD_Q3 | 0.0713 | 0.0299 | 8.45E-03 | 0.0000 | 0.0291 | 5.00E-01 | |
| 0.01 < MAF ≤ 0.1; LD_Q4 | 0.0053 | 0.0211 | 4.01E-01 | 0.0014 | 0.0214 | 4.74E-01 | |
| 0.1 < MAF ≤ 0.2; LD_Q1 | 0.0502 | 0.0395 | 1.02E-01 | 0.0279 | 0.0410 | 2.48E-01 | |
| 0.1 < MAF ≤ 0.2; LD_Q2 | 0.0143 | 0.0380 | 3.54E-01 | 0.0143 | 0.0378 | 3.53E-01 | |
| 0.1 < MAF ≤ 0.2; LD_Q3 | 0.0166 | 0.0344 | 3.15E-01 | 0.0000 | 0.0354 | 5.00E-01 | |
| 0.1 < MAF ≤ 0.2; LD_Q4 | 0.0473 | 0.0272 | 4.11E-02 | 0.0530 | 0.0283 | 3.07E-02 | |
| 0.2 < MAF ≤ 0.3; LD_Q1 | 0.0000 | 0.0379 | 5.00E-01 | 0.0250 | 0.0398 | 2.65E-01 | |
| 0.2 < MAF ≤ 0.3; LD_Q2 | 0.0668 | 0.0373 | 3.67E-02 | 0.0507 | 0.0380 | 9.10E-02 | |
| 0.2 < MAF ≤ 0.3; LD_Q3 | 0.0710 | 0.0362 | 2.50E-02 | 0.0050 | 0.0354 | 4.44E-01 | |
| 0.2 < MAF ≤ 0.3; LD_Q4 | 0.0000 | 0.0276 | 5.00E-01 | 0.0081 | 0.0282 | 3.87E-01 | |
| 0.3 < MAF ≤ 0.4; LD_Q1 | 0.0556 | 0.0383 | 7.37E-02 | 0.0010 | 0.0392 | 4.89E-01 | |
| 0.3 < MAF ≤ 0.4; LD_Q2 | 0.0001 | 0.0360 | 4.99E-01 | 0.0000 | 0.0361 | 5.00E-01 | |
| 0.3 < MAF ≤ 0.4; LD_Q3 | 0.0000 | 0.0345 | 5.00E-01 | 0.0000 | 0.0345 | 5.00E-01 | |
| 0.3 < MAF ≤ 0.4; LD_Q4 | 0.0425 | 0.0290 | 7.12E-02 | 0.0000 | 0.0276 | 5.00E-01 | |
| 0.4 < MAF ≤ 0.5; LD_Q1 | 0.0766 | 0.0358 | 1.62E-02 | 0.0254 | 0.0360 | 2.40E-01 | |
| 0.4 < MAF ≤ 0.5; LD_Q2 | 0.0436 | 0.0336 | 9.72E-02 | 0.0000 | 0.0334 | 5.00E-01 | |
| 0.4 < MAF ≤ 0.5; LD_Q3 | 0.0035 | 0.0307 | 4.54E-01 | 0.0457 | 0.0319 | 7.56E-02 | |
| 0.4 < MAF ≤ 0.5; LD_Q4 | 0.0201 | 0.0246 | 2.06E-01 | 0.0157 | 0.0257 | 2.72E-01 | |
| GREML-LDMS-I | 0.01 < MAF ≤ 0.1; LD_Q1 | 0.0340 | 0.0462 | 2.31E-01 | 0.0000 | 0.0486 | 5.00E-01 |
| 0.01 < MAF ≤ 0.1; LD_Q2 | 0.0462 | 0.0284 | 5.18E-02 | 0.0000 | 0.0283 | 5.00E-01 | |
| 0.01 < MAF ≤ 0.1; LD_Q3 | 0.0107 | 0.0190 | 2.87E-01 | 0.0064 | 0.0192 | 3.70E-01 | |
| 0.01 < MAF ≤ 0.1; LD_Q4 | 0.0000 | 0.0099 | 5.00E-01 | 0.0050 | 0.0109 | 3.22E-01 | |
| 0.1 < MAF ≤ 0.2; LD_Q1 | 0.0786 | 0.0452 | 4.11E-02 | 0.0364 | 0.0460 | 2.14E-01 | |
| 0.1 < MAF ≤ 0.2; LD_Q2 | 0.0071 | 0.0404 | 4.30E-01 | 0.0108 | 0.0410 | 3.96E-01 | |
| 0.1 < MAF ≤ 0.2; LD_Q3 | 0.0000 | 0.0334 | 5.00E-01 | 0.0019 | 0.0336 | 4.77E-01 | |
| 0.1 < MAF ≤ 0.2; LD_Q4 | 0.0599 | 0.0230 | 4.58E-03 | 0.0309 | 0.0227 | 8.70E-02 | |
| 0.2 < MAF ≤ 0.3; LD_Q1 | 0.0000 | 0.0374 | 5.00E-01 | 0.0004 | 0.0381 | 4.96E-01 | |
| 0.2 < MAF ≤ 0.3; LD_Q2 | 0.0854 | 0.0405 | 1.76E-02 | 0.0562 | 0.0404 | 8.21E-02 | |
| 0.2 < MAF ≤ 0.3; LD_Q3 | 0.0137 | 0.0358 | 3.51E-01 | 0.0002 | 0.0380 | 4.98E-01 | |
| 0.2 < MAF ≤ 0.3; LD_Q4 | 0.0249 | 0.0282 | 1.89E-01 | 0.0156 | 0.0283 | 2.91E-01 | |
| 0.3 < MAF ≤ 0.4; LD_Q1 | 0.0700 | 0.0334 | 1.82E-02 | 0.0000 | 0.0347 | 5.00E-01 | |
| 0.3 < MAF ≤ 0.4; LD_Q2 | 0.0000 | 0.0378 | 5.00E-01 | 0.0000 | 0.0391 | 5.00E-01 | |
| 0.3 < MAF ≤ 0.4; LD_Q3 | 0.0219 | 0.0372 | 2.77E-01 | 0.0000 | 0.0379 | 5.00E-01 | |
| 0.3 < MAF ≤ 0.4; LD_Q4 | 0.0295 | 0.0309 | 1.70E-01 | 0.0000 | 0.0300 | 5.00E-01 | |
| 0.4 < MAF ≤ 0.5; LD_Q1 | 0.0141 | 0.0314 | 3.27E-01 | 0.0000 | 0.0316 | 5.00E-01 | |
| 0.4 < MAF ≤ 0.5; LD_Q2 | 0.0938 | 0.0362 | 4.79E-03 | 0.0483 | 0.0372 | 9.68E-02 | |
| 0.4 < MAF ≤ 0.5; LD_Q3 | 0.0060 | 0.0346 | 4.31E-01 | 0.0211 | 0.0358 | 2.78E-01 | |
| 0.4 < MAF ≤ 0.5; LD_Q4 | 0.0195 | 0.0278 | 2.41E-01 | 0.0196 | 0.0292 | 2.51E-01 | |
| LDAK-Thin-MS | 0.01 < MAF ≤ 0.1 | 0.1112 | 0.0554 | 2.24E-02 | −0.0201 | 0.0539 | 3.54E-01 |
| 0.1 < MAF ≤ 0.2 | 0.1243 | 0.0695 | 3.68E-02 | 0.1175 | 0.0704 | 4.76E-02 | |
| 0.2 < MAF ≤ 0.3 | 0.0820 | 0.0699 | 1.20E-01 | 0.0822 | 0.0696 | 1.19E-01 | |
| 0.3 < MAF ≤ 0.4 | 0.1306 | 0.0703 | 3.17E-02 | −0.0518 | 0.0692 | 2.27E-01 | |
| 0.4 < MAF ≤ 0.5 | 0.1495 | 0.0630 | 8.82E-03 | 0.1250 | 0.0639 | 2.53E-02 | |
| LDAK-MS | 0.01 < MAF ≤ 0.1 | 0.0767 | 0.0569 | 8.88E-02 | −0.0034 | 0.0569 | 4.76E-01 |
| 0.1 < MAF ≤ 0.2 | 0.1769 | 0.0678 | 4.52E-03 | 0.1525 | 0.0691 | 1.37E-02 | |
| 0.2 < MAF ≤ 0.3 | 0.0763 | 0.0623 | 1.10E-01 | 0.0970 | 0.0626 | 6.05E-02 | |
| 0.3 < MAF ≤ 0.4 | 0.1576 | 0.0585 | 3.52E-03 | −0.0099 | 0.0591 | 4.33E-01 | |
| 0.4 < MAF ≤ 0.5 | 0.1298 | 0.0570 | 1.14E-02 | 0.0237 | 0.0567 | 3.38E-01 | |
- a MS, LDMS-R, LDMS-I represent MAF stratified, Regional LD scores and MAF stratified, Individual SNP LD score and MAF stratified, respectively; LD_Q1-4 represent quartiles one to four based on regional or SNP LD scores. p-values were calculated using one sided z test.
CONCLUSION AND FUTURE DIRECTION
Heritability has been widely used to improve the quality of crops and farm animals, to understand the genetic basis of complex human traits and diseases, and to estimate the response of evolutionary forces such as selection in a population. However, the utility of heritability has been limited to a certain extent, mainly due to lack of appropriate data types and heritability models. Over the past decade, several approaches fitting a variety of analytical models have been developed to estimate SNP-heritability in unrelated individuals. In the current review, we provide an overview of these approaches along with step-by-step protocol to run widely used approaches for SNP-heritability estimation.
Despite advances in heritability models and availability of genome-wide SNP information in large datasets, estimates of
AUTHOR CONTRIBUTIONS
Amit K. Srivastava : Conceptualization, data curation, formal analysis, investigation, methodology, resources, software, validation, visualization, writing original draft, writing review and editing; Scott M. Williams : writing review and editing; Ge Zhang : conceptualization, data curation, funding acquisition, investigation, project administration, resources, supervision, writing review and editing.
CONFLICT OF INTEREST
Authors declare no conflict of interest.
Open Research
DATA AVAILABILITY STATEMENT
Individual-level genetic data that support the protocol (The Northern Finland Birth Cohort) are available in dbGaP for general research use (https://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?study_id=phs000276.v2.p1). Likewise, summary results are openly available in GIANT consortium datafiles (https://portals.broadinstitute.org/collaboration/giant/index.php/GIANT_consortium_data_files).
LITERATURE CITED
- 1000 Genomes Project Consortium, Abecasis, G. R., Altshuler, D., Auton, A., Brooks, L. D., Durbin, R. M., Gibbs, R. A., Hurles, M. E., & McVean, G. A. (2010). A map of human genome variation from population-scale sequencing. Nature , 467(7319), 1061–1073. https://doi.org/10.1038/nature09534
- 1000 Genomes Project Consortium, Abecasis, G. R., Auton, A., Brooks, L. D., DePristo, M. A., Durbin, R. M., Handsaker, R. E., Kang, H. M., Marth, G. T., & McVean, G. A. (2012). An integrated map of genetic variation from 1,092 human genomes. Nature , 491(7422), 56–65. https://doi.org/10.1038/nature11632
- 1000 Genomes Project Consortium, Auton, A., Brooks, L. D., Durbin, R. M., Garrison, E. P., Kang, H. M., Korbel, J. O., Marchini, J. L., McCarthy, S., McVean, G. A., & Abecasis, G. R. (2015). A global reference for human genetic variation. Nature , 526(7571), 68–74. https://doi.org/10.1038/nature15393
- Allison, D. B., Kaprio, J., Korkeila, M., Koskenvuo, M., Neale, M. C., & Hayakawa, K. (1996). The heritability of body mass index among an international sample of monozygotic twins reared apart. International Journal of Obesity and Related Metabolic Disorders , 20(6), 501–506. Retrieved from https://www.ncbi.nlm.nih.gov/pubmed/8782724
- Bateson, W. (1922). Genetical analysis and the theory of natural selection. Science , 55(1423), 373. https://doi.org/10.1126/science.55.1423.373
- Bernardo, R. (2020). Reinventing quantitative genetics for plant breeding: Something old, something new, something borrowed, something BLUE. Heredity (Edinb) , 125(6), 375–385. https://doi.org/10.1038/s41437-020-0312-1
- Berry, D. P., Buckley, F., Dillon, P., Evans, R. D., Rath, M., & Veerkamp, R. F. (2003). Genetic parameters for body condition score, body weight, milk yield, and fertility estimated using random regression models. Journal of Dairy Science , 86(11), 3704–3717. https://doi.org/10.3168/jds.S0022-0302(03)73976-9
- Berry, D. P., Wall, E., & Pryce, J. E. (2014). Genetics and genomics of reproductive performance in dairy and beef cattle. Animal , 8(Suppl 1), 105–121. https://doi.org/10.1017/S1751731114000743
- Boomsma, D., Busjahn, A., & Peltonen, L. (2002). Classical twin studies and beyond. Nature Reviews Genetics , 3(11), 872–882. https://doi.org/10.1038/nrg932
- Brookfield, J. F. (2013). Quantitative genetics: Heritability is not always missing. Current Biology , 23(7), R276–278. https://doi.org/10.1016/j.cub.2013.02.040
- Browning, S. R., & Browning, B. L. (2012). Identity by descent between distant relatives: Detection and applications. Annual Review of Genetics , 46, 617–633. https://doi.org/10.1146/annurev-genet-110711-155534
- Browning, S. R., & Browning, B. L. (2013). Identity-by-descent-based heritability analysis in the Northern Finland Birth Cohort. Human Genetics , 132(2), 129–138. https://doi.org/10.1007/s00439-012-1230-y
- Bulik-Sullivan, B., Finucane, H. K., Anttila, V., Gusev, A., Day, F. R., Loh, P.- R., Duncan, L., Perry, J. R. B., Patterson, N., Robinson, E. B., Daly, M. J., Price, A. L., & Neale, B. M. (2015). An atlas of genetic correlations across human diseases and traits. Nature Genetics , 47(11), 1236–1241. https://doi.org/10.1038/ng.3406
- Bulik-Sullivan, B. K., Loh, P. R., Finucane, H. K., Ripke, S., Yang, J., Schizophrenia Working Group of the Psychiatric Genomics Consortium, Patterson, N., Daly, M. J., Price, A. L., & Neale, B. M. (2015). LD Score regression distinguishes confounding from polygenicity in genome-wide association studies. Nature Genetics , 47(3), 291–295. https://doi.org/10.1038/ng.3211
- Buniello, A., Macarthur, J. A. L., Cerezo, M., Harris, L. W., Hayhurst, J., Malangone, C., Mcmahon, A., Morales, J., Mountjoy, E., Sollis, E., Suveges, D., Vrousgou, O., Whetzel, P. L., Amode, R., Guillen, J. A., Riat, H. S., Trevanion, S. J., Hall, P., Junkins, H., … Parkinson, H. (2019). The NHGRI-EBI GWAS Catalog of published genome-wide association studies, targeted arrays and summary statistics 2019. Nucleic Acids Research , 47(D1), D1005–D1012. https://doi.org/10.1093/nar/gky1120
- Cassell, B. G. (2009). Using heritability for genetic improvement. Available at: https://static.yanyin.tech/literature/current_protocol/10.1002/cpz1.734/attachments/404-084_pdf.pdf
- Chang, C. C., Chow, C. C., Tellier, L. C., Vattikuti, S., Purcell, S. M., & Lee, J. J. (2015). Second-generation PLINK: Rising to the challenge of larger and richer datasets. Gigascience , 4, 7. https://doi.org/10.1186/s13742-015-0047-8
- Dempster, E. R., & Lerner, I. M. (1950). Heritability of threshold characters. Genetics , 35(2), 212–236. https://doi.org/10.1093/genetics/35.2.212
- Eaves, L. J., Last, K. A., Young, P. A., & Martin, N. G. (1978). Model-fitting approaches to the analysis of human behaviour. Heredity (Edinb) , 41(3), 249–320. Retrieved from https://www.ncbi.nlm.nih.gov/pubmed/370072
- Eichler, E. E., Flint, J., Gibson, G., Kong, A., Leal, S. M., Moore, J. H., & Nadeau, J. H. (2010). Missing heritability and strategies for finding the underlying causes of complex disease. Nature Reviews Genetics , 11(6), 446–450. https://doi.org/10.1038/nrg2809
- Evans, L. M., Tahmasbi, R., Jones, M., Vrieze, S. I., Abecasis, G. R., Das, S., Bjelland, D. W., De Candia, T. R., Yang, J., Goddard, M. E., Visscher, P. M., Keller, M. C., & Haplotype Reference Consortium. (2018). Narrow-sense heritability estimation of complex traits using identity-by-descent information. Heredity (Edinb) , 121(6), 616–630. https://doi.org/10.1038/s41437-018-0067-0
- Evans, L. M., Tahmasbi, R., Vrieze, S. I., Abecasis, G. R., Das, S., Gazal, S., Bjelland, D. W., De Candia, T. R., Goddard, M. E., Neale, B. M., Yang, J., Visscher, P. M., & Keller, M. C. (2018). Comparison of methods that use whole genome data to estimate the heritability and genetic architecture of complex traits. Nature Genetics , 50(5), 737–745. https://doi.org/10.1038/s41588-018-0108-x
- Falconer, D. S. (1960). Introduction to quantitative genetics ( 1 ed.). Oliver & Boyd.
- Falconer, D. S. (1965). Inheritance of liability to certain diseases, estimated from the incidence among relatives. Annals of Human Genetics , 29(1), 51–76.
- Finucane, H. K., Bulik-Sullivan, B., Gusev, A., Trynka, G., Reshef, Y., Loh, P.- R., Anttila, V., Xu, H., Zang, C., Farh, K., Ripke, S., Day, F. R., Purcell, S., Stahl, E., Lindstrom, S., Perry, J. R. B., Okada, Y., Raychaudhuri, S., Daly, M. J., … Price, A. L. (2015). Partitioning heritability by functional annotation using genome-wide association summary statistics. Nature Genetics , 47(11), 1228–1235. https://doi.org/10.1038/ng.3404
- Fisher, R. A. (1918). The correlation between relatives on the supposition of mendelian inheritance. Transactions of the Royal Society of Edinburgh , 52, 35.
- Fisher, R. A. (1930). The genetical theory of natural selection. Clarendon Press.
- Friedman, N. P., Banich, M. T., & Keller, M. C. (2021). Twin studies to GWAS: There and back again. Trends in Cognitive Sciences , 25(10), 855–869. https://doi.org/10.1016/j.tics.2021.06.007
- Genin, E. (2020). Missing heritability of complex diseases: Case solved? Human Genetics , 139(1), 103–113. https://doi.org/10.1007/s00439-019-02034-4
- Gibson, G. (2012). Rare and common variants: Twenty arguments. Nature Reviews Genetics , 13(2), 135–145. https://doi.org/10.1038/nrg3118
- Golan, D., Lander, E. S., & Rosset, S. (2014). Measuring missing heritability: Inferring the contribution of common variants. Proceedings of the National Academy of Sciences of the United States of America , 111(49), E5272–5281. https://doi.org/10.1073/pnas.1419064111
- Grant, P. R., & Grant, B. R. (1995). Predicting microevolutionary responses to directional selection on heritable variation. Evolution; International Journal of Organic Evolution , 49(2), 241–251. https://doi.org/10.1111/j.1558-5646.1995.tb02236.x
- Hadfield, J. D. (2008). Estimating evolutionary parameters when viability selection is operating. Proceedings: Biological Sciences , 275(1635), 723–734. https://doi.org/10.1098/rspb.2007.1013
- Hall, J. B., & Bush, W. S. (2016). Analysis of heritability using genome-wide data. Current Protocols in Human Genetics , 91, 1.30.31–31.30.10. https://doi.org/10.1002/cphg.25
- Haseman, J. K., & Elston, R. C. (1972). The investigation of linkage between a quantitative trait and a marker locus. Behavior Genetics , 2(1), 3–19. https://doi.org/10.1007/BF01066731
- Hou, K., Burch, K. S., Majumdar, A., Shi, H., Mancuso, N., Wu, Y., Sankararaman, S., & Pasaniuc, B. (2019). Accurate estimation of SNP-heritability from biobank-scale data irrespective of genetic architecture. Nature Genetics , 51(8), 1244–1251. https://doi.org/10.1038/s41588-019-0465-0
- Institute of Medicine. (2006). Genetics and Health. In L. M. Hernandez & D. G. Blazer (Eds.), Genes, behavior, and the social environment: Moving beyond the nature/nurture debate (pp. 384). Washington, DC: The National Academies Press.
- International HapMap, C. (2005). A haplotype map of the human genome. Nature , 437(7063), 1299–1320. https://doi.org/10.1038/nature04226
- Kelly, J. K. (2011). The breeder's equation. Nature Education Knowledge , 4(5), 5. Retrieved from https://www.nature.com/scitable/knowledge/library/the-breeder-s-equation-24204828/
- Kingsolver, J. G., Hoekstra, H. E., Hoekstra, J. M., Berrigan, D., Vignieri, S. N., Hill, C. E., Hoang, A., Gibert, P., & Beerli, P. (2001). The strength of phenotypic selection in natural populations. American Naturalist , 157(3), 245–261. https://doi.org/10.1086/319193
- Lande, R., & Arnold, S. J. (1983). The measurement of selection on correlated characters. Evolution; Internation Journal of Organic Evolution , 37(6), 1210–1226. https://doi.org/10.1111/j.1558-5646.1983.tb00236.x
- Lee, S. H., Goddard, M. E., Visscher, P. M., & van der Werf, J. H. (2010). Using the realized relationship matrix to disentangle confounding factors for the estimation of genetic variance components of complex traits. Genetics, Selection, Evolution , 42(1), 22. https://doi.org/10.1186/1297-9686-42-22
- Lee, S. H., & van der Werf, J. H. (2006). An efficient variance component approach implementing an average information REML suitable for combined LD and linkage mapping with a general complex pedigree. Genetics, Selection, Evolution , 38(1), 25–43. https://doi.org/10.1051/gse:2005025
- Lee, S. H., Wray, N. R., Goddard, M. E., & Visscher, P. M. (2011). Estimating missing heritability for disease from genome-wide association studies. American Journal of Human Genetics , 88(3), 294–305. https://doi.org/10.1016/j.ajhg.2011.02.002
- Lunde, A., Melve, K. K., Gjessing, H. K., Skjaerven, R., & Irgens, L. M. (2007). Genetic and environmental influences on birth weight, birth length, head circumference, and gestational age by use of population-based parent-offspring data. American Journal of Epidemiology , 165(7), 734–741. https://doi.org/10.1093/aje/kwk107
- Manjula, P., Park, H. - B., Seo, D., Choi, N., Jin, S., Ahn, S. J., Heo, K. N., Kang, B. S., & Lee, J. H. (2018). Estimation of heritability and genetic correlation of body weight gain and growth curve parameters in Korean native chicken. Asian-Australasian Journal of Animal Sciences , 31(1), 26–31. https://doi.org/10.5713/ajas.17.0179
- Manolio, T. A., Collins, F. S., Cox, N. J., Goldstein, D. B., Hindorff, L. A., Hunter, D. J., Mccarthy, M. I., Ramos, E. M., Cardon, L. R., Chakravarti, A., Cho, J. H., Guttmacher, A. E., Kong, A., Kruglyak, L., Mardis, E., Rotimi, C. N., Slatkin, M., Valle, D., Whittemore, A. S., … Visscher, P. M. (2009). Finding the missing heritability of complex diseases. Nature , 461(7265), 747–753. https://doi.org/10.1038/nature08494
- Maroilley, T., & Tarailo-Graovac, M. (2019). Uncovering missing heritability in rare diseases. Genes (Basel) , 10(4), 275. https://doi.org/10.3390/genes10040275
- Mayhew, A. J., & Meyre, D. (2017). Assessing the heritability of complex traits in humans: Methodological challenges and opportunities. Current Genomics , 18(4), 332–340. https://doi.org/10.2174/1389202918666170307161450
- Miglior, F., Fleming, A., Malchiodi, F., Brito, L. F., Martin, P., & Baes, C. F. (2017). A 100-Year Review: Identification and genetic selection of economically important traits in dairy cattle. Journal of Dairy Science , 100(12), 10251–10271. https://doi.org/10.3168/jds.2017-12968
- Mousseau, T. A., & Roff, D. A. (1987). Natural selection and the heritability of fitness components. Heredity (Edinb) , 59(Pt 2), 181–197. https://doi.org/10.1038/hdy.1987.113
- Nance, W. E., Kramer, A. A., Corey, L. A., Winter, P. M., & Eaves, L. J. (1983). A causal analysis of birth weight in the offspring of monozygotic twins. American Journal of Human Genetics , 35(6), 1211–1223. Retrieved from https://www.ncbi.nlm.nih.gov/pubmed/6685976
- Ni, G., Moser, G., Schizophrenia Working Group of the Psychiatric Genomics Consortium, Wray, N. R., & Lee, S. H. (2018). Estimation of genetic correlation via linkage disequilibrium score regression and genomic restricted maximum likelihood. American Journal of Human Genetics , 102(6), 1185–1194. https://doi.org/10.1016/j.ajhg.2018.03.021
- Palmquist, D. L., & Jenkins, T. C. (2017). A 100-Year Review: Fat feeding of dairy cows. Journal of Dairy Science , 100(12), 10061–10077. https://doi.org/10.3168/jds.2017-12924
- Pasaniuc, B., & Price, A. L. (2017). Dissecting the genetics of complex traits using summary association statistics. Nature Reviews Genetics , 18(2), 117–127. https://doi.org/10.1038/nrg.2016.142
- Powell, J. E., Visscher, P. M., & Goddard, M. E. (2010). Reconciling the analysis of IBD and IBS in complex trait studies. Nature Reviews Genetics , 11(11), 800–805. https://doi.org/10.1038/nrg2865
- Purcell, S., Neale, B., Todd-Brown, K., Thomas, L., Ferreira, M. A. R., Bender, D., Maller, J., Sklar, P., De Bakker, P. I. W., Daly, M. J., & Sham, P. C. (2007). PLINK: A tool set for whole-genome association and population-based linkage analyses. American Journal of Human Genetics , 81(3), 559–575. https://doi.org/10.1086/519795
- Ritland, K. (1996). A marker-based method for inferences about quantitative inheritance in natural populations. Evolution: International Journal of Organic Evolution , 50(3), 1062–1073. https://doi.org/10.1111/j.1558-5646.1996.tb02347.x
- Ritland, K. (2000). Marker-inferred relatedness as a tool for detecting heritability in nature. Molecular Ecology , 9(9), 1195–1204. https://doi.org/10.1046/j.1365-294x.2000.00971.x
- Sabatti, C., Service, S. K., Hartikainen, A. - L., Pouta, A., Ripatti, S., Brodsky, J., Jones, C. G., Zaitlen, N. A., Varilo, T., Kaakinen, M., Sovio, U., Ruokonen, A., Laitinen, J., Jakkula, E., Coin, L., Hoggart, C., Collins, A., Turunen, H., Gabriel, S., … Peltonen, L. (2009). Genome-wide association analysis of metabolic traits in a birth cohort from a founder population. Nature Genetics , 41(1), 35–46. https://doi.org/10.1038/ng.271
- Sham, P. C., & Purcell, S. (2001). Equivalence between Haseman-Elston and variance-components linkage analyses for sib pairs. American Journal of Human Genetics , 68(6), 1527–1532. https://doi.org/10.1086/320593
- Silventoinen, K., Sammalisto, S., Perola, M., Boomsma, D. I., Cornes, B. K., Davis, C., Dunkel, L., De Lange, M., Harris, J. R., Hjelmborg, J. V. B., Luciano, M., Martin, N. G., Mortensen, J., Nisticò, L., Pedersen, N. L., Skytthe, A., Spector, T. D., Stazi, M. A., Willemsen, G., & Kaprio, J. (2003). Heritability of adult body height: A comparative study of twin cohorts in eight countries. Twin Research , 6(5), 399–408. https://doi.org/10.1375/136905203770326402
- Speed, D., & Balding, D. J. (2015). Relatedness in the post-genomic era: Is it still useful? Nature Reviews Genetics , 16(1), 33–44. https://doi.org/10.1038/nrg3821
- Speed, D., & Balding, D. J. (2019). SumHer better estimates the SNP heritability of complex traits from summary statistics. Nature Genetics , 51(2), 277–284. https://doi.org/10.1038/s41588-018-0279-5
- Speed, D., Cai, N., Consortium, U., Johnson, M. R., Nejentsev, S., & Balding, D. J. (2017). Reevaluation of SNP heritability in complex human traits. Nature Genetics , 49(7), 986–992. https://doi.org/10.1038/ng.3865
- Speed, D., Hemani, G., Johnson, M. R., & Balding, D. J. (2012). Improved heritability estimation from genome-wide SNPs. American Journal of Human Genetics , 91(6), 1011–1021. https://doi.org/10.1016/j.ajhg.2012.10.010
- Speed, D., Holmes, J., & Balding, D. J. (2020). Evaluating and improving heritability models using summary statistics. Nature Genetics , 52(4), 458–462. https://doi.org/10.1038/s41588-020-0600-y
- Stunkard, A. J., Harris, J. R., Pedersen, N. L., & McClearn, G. E. (1990). The body-mass index of twins who have been reared apart. New England Journal of Medicine , 322(21), 1483–1487. https://doi.org/10.1056/NEJM199005243222102
- Tang, M., Wang, T., & Zhang, X. (2022). A review of SNP heritability estimation methods. Briefings in Bioinformatics , 23(3), bbac067. https://doi.org/10.1093/bib/bbac067
- R Team. (2019). RStudio: Integrated development for R. RStudio, Inc. Retrieved from http://www.rstudio.com/
- R Team. (2020). R: A language and environment for statistical computing. R Foundation for Statistical Computing. Retrieved from https://www.R-project.org/
- Tenesa, A., & Haley, C. S. (2013). The heritability of human disease: Estimation, uses and abuses. Nature Reviews Genetics , 14(2), 139–149. https://doi.org/10.1038/nrg3377
- Thomas, S. C. (2005). The estimation of genetic relationships using molecular markers and their efficiency in estimating heritability in natural populations. Philosophical Transactions of the Royal Society of London. Series B: Biological Sciences , 360(1459), 1457–1467. https://doi.org/10.1098/rstb.2005.1675
- Thompson, H. D. P. A. R. (1971). Recovery of inter-block information when block sizes are unequal. Biometrika , 58(3), 545–554.
- Truong, V. Q., Woerner, J. A., Cherlin, T. A., Bradford, Y., Lucas, A. M., Okeh, C. C., Shivakumar, M. K., Hui, D. H., Kumar, R., Pividori, M., Jones, S. C., Bossa, A. C., Turner, S. D., Ritchie, M. D., & Verma, S. S. (2022). Quality control procedures for genome-wide association studies. Current Protocols , 2(11), e603. https://doi.org/10.1002/cpz1.603
- Turner, S., Armstrong, L., Bradford, Y., Carlson, C. S., Crawford, D. C., Crenshaw, A. T., De Andrade, M., Doheny, K. F., Haines, J. L., Hayes, G., Jarvik, G., Jiang, L., Kullo, I. J., Li, R., Ling, H., Manolio, T. A., Matsumoto, M., Mccarty, C. A., Mcdavid, A. N., … Ritchie, M. D. (2011). Quality control procedures for genome-wide association studies. Current Protocols in Human Genetics , 68, 1.19.1–1.19.18. https://doi.org/10.1002/0471142905.hg0119s68
- Uricchio, L. H. (2020). Evolutionary perspectives on polygenic selection, missing heritability, and GWAS. Human Genetics , 139(1), 5–21. https://doi.org/10.1007/s00439-019-02040-6
- Utrera, A. R., & Van Vleck, L. D. (2004). Heritability estimates for carcass traits of cattle: A review. Genetics and Molecular Research [Electronic Resource] , 3(3), 380–394. Retrieved from https://www.ncbi.nlm.nih.gov/pubmed/15614729
- VanRaden, P. M. (2008). Efficient methods to compute genomic predictions. Journal of Dairy Science , 91(11), 4414–4423. https://doi.org/10.3168/jds.2007-0980
- Velasco, L., & Fernández-martínez, J. M. (2002). Breeding oilseed crops for improved oil quality. Journal of Crop Production , 5(1-2), 309–344. https://doi.org/10.1300/J144v05n01_13
- Villanueva-Mejia, D., & Alvarez, J. D. (2017). Genetic improvement of oilseed crops using modern biotechnology. In J. C. Jimenez-Lopez (Ed.), Advances in seed biology. Available at https://www.intechopen.com/chapters/57027
- Vinkhuyzen, A. A., Wray, N. R., Yang, J., Goddard, M. E., & Visscher, P. M. (2013). Estimation and partition of heritability in human populations using whole-genome analysis methods. Annual Review of Genetics , 47, 75–95. https://doi.org/10.1146/annurev-genet-111212-133258
- Visscher, P. M., & Goddard, M. E. (2019). From R.A. Fisher's 1918 paper to GWAS a century later. Genetics , 211(4), 1125–1130. https://doi.org/10.1534/genetics.118.301594
- Visscher, P. M., Hill, W. G., & Wray, N. R. (2008). Heritability in the genomics era–concepts and misconceptions. Nature Reviews Genetics , 9(4), 255–266. https://doi.org/10.1038/nrg2322
- Visscher, P. M., Macgregor, S., Benyamin, B., Zhu, G., Gordon, S., Medland, S., Hill, W. G., Hottenga, J. - J., Willemsen, G., Boomsma, D. I., Liu, Y. - Z., Deng, H. - W., Montgomery, G. W., & Martin, N. G. (2007). Genome partitioning of genetic variation for height from 11,214 sibling pairs. American Journal of Human Genetics , 81(5), 1104–1110. https://doi.org/10.1086/522934
- Visscher, P. M., McEvoy, B., & Yang, J. (2010). From Galton to GWAS: Quantitative genetics of human height. Genetics Research , 92(5-6), 371–379. https://doi.org/10.1017/S0016672310000571
- Visscher, P. M., Medland, S. E., Ferreira, M. A. R., Morley, K. I., Zhu, G., Cornes, B. K., Montgomery, G. W., & Martin, N. G. (2006). Assumption-free estimation of heritability from genome-wide identity-by-descent sharing between full siblings. PloS Genetics , 2(3), e41. https://doi.org/10.1371/journal.pgen.0020041
- Walsh, M. L. A. B. (1998). Genetics and analysis of quantitative traits. Sinauer Associates, Inc.
- Weale, M. E. (2010). Quality control for genome-wide association studies. Methods in Molecular Biology , 628, 341–372. https://doi.org/10.1007/978-1-60327-367-1_19
- Weir, B. S., Anderson, A. D., & Hepler, A. B. (2006). Genetic relatedness analysis: Modern data and new challenges. Nature Reviews Genetics , 7(10), 771–780. https://doi.org/10.1038/nrg1960
- Wood, J. L., Yates, M. C., & Fraser, D. J. (2016). Are heritability and selection related to population size in nature? Meta-analysis and conservation implications. Evolutionary Applications , 9(5), 640–657. https://doi.org/10.1111/eva.12375
- Wray, N. R., Goddard, M. E., & Visscher, P. M. (2007). Prediction of individual genetic risk to disease from genome-wide association studies. Genome Research , 17(10), 1520–1528. https://doi.org/10.1101/gr.6665407
- Wray, N. R., Yang, J., Hayes, B. J., Price, A. L., Goddard, M. E., & Visscher, P. M. (2013). Pitfalls of predicting complex traits from SNPs. Nature Reviews Genetics , 14(7), 507–515. https://doi.org/10.1038/nrg3457
- Wright, S. (1921). Systems of mating. I. The biometric relations between parent and offspring. Genetics , 6(2), 111–123. https://doi.org/10.1093/genetics/6.2.111
- Yang, J., Bakshi, A., Zhu, Z., Hemani, G., Vinkhuyzen, A. A. E., Lee, S. H., Robinson, M. R., Perry, J. R. B., Nolte, I. M., Van Vliet-Ostaptchouk, J. V., Snieder, H., Esko, T., Milani, L., Mägi, R., Metspalu, A., Hamsten, A., Magnusson, P. K. E., Pedersen, N. L., Ingelsson, E., … Visscher, P. M. (2015). Genetic variance estimation with imputed variants finds negligible missing heritability for human height and body mass index. Nature Genetics , 47(10), 1114–1120. https://doi.org/10.1038/ng.3390
- Yang, J., Benyamin, B., Mcevoy, B. P., Gordon, S., Henders, A. K., Nyholt, D. R., Madden, P. A., Heath, A. C., Martin, N. G., Montgomery, G. W., Goddard, M. E., & Visscher, P. M. (2010). Common SNPs explain a large proportion of the heritability for human height. Nature Genetics , 42(7), 565–569. https://doi.org/10.1038/ng.608
- Yang, J., Lee, S. H., Goddard, M. E., & Visscher, P. M. (2011). GCTA: A tool for genome-wide complex trait analysis. American Journal of Human Genetics , 88(1), 76–82. https://doi.org/10.1016/j.ajhg.2010.11.011
- Yang, J., Lee, S. H., Goddard, M. E., & Visscher, P. M. (2013). Genome-wide complex trait analysis (GCTA): Methods, data analyses, and interpretations. Methods in Molecular Biology , 1019, 215–236. https://doi.org/10.1007/978-1-62703-447-0_9
- Yang, J., Manolio, T. A., Pasquale, L. R., Boerwinkle, E., Caporaso, N., Cunningham, J. M., De Andrade, M., Feenstra, B., Feingold, E., Hayes, M. G., Hill, W. G., Landi, M. T., Alonso, A., Lettre, G., Lin, P., Ling, H., Lowe, W., Mathias, R. A., Melbye, M., … Visscher, P. M. (2011). Genome partitioning of genetic variation for complex traits using common SNPs. Nature Genetics , 43(6), 519–525. https://doi.org/10.1038/ng.823
- Yang, J., Zaitlen, N. A., Goddard, M. E., Visscher, P. M., & Price, A. L. (2014). Advantages and pitfalls in the application of mixed-model association methods. Nature Genetics , 46(2), 100–106. https://doi.org/10.1038/ng.2876
- Yang, J., Zeng, J., Goddard, M. E., Wray, N. R., & Visscher, P. M. (2017). Concepts, estimation and interpretation of SNP-based heritability. Nature Genetics , 49(9), 1304–1310. https://doi.org/10.1038/ng.3941
- Yengo, L., Sidorenko, J., Kemper, K. E., Zheng, Z., Wood, A. R., Weedon, M. N., Frayling, T. M., Hirschhorn, J., Yang, J., Visscher, P. M., & GIANT Consortium. (2018). Meta-analysis of genome-wide association studies for height and body mass index in approximately 700000 individuals of European ancestry. Human Molecular Genetics , 27(20), 3641–3649. https://doi.org/10.1093/hmg/ddy271
- Zaitlen, N., & Kraft, P. (2012). Heritability in the genome-wide association era. Human Genetics , 131(10), 1655–1664. https://doi.org/10.1007/s00439-012-1199-6
- Zaitlen, N., Kraft, P., Patterson, N., Pasaniuc, B., Bhatia, G., Pollack, S., & Price, A. L. (2013). Using extended genealogy to estimate components of heritability for 23 quantitative and dichotomous traits. PloS Genetics , 9(5), e1003520. https://doi.org/10.1371/journal.pgen.1003520
- Zhang, G. (2015). Genetic architecture of complex human traits: What have we learned from genome-wide association studies? Current Genetic Medicine Reports , 3(4), 143–150. https://doi.org/10.1007/s40142-015-0083-9
- Zhang, Q., Prive, F., Vilhjalmsson, B., & Speed, D. (2021). Improved genetic prediction of complex traits from individual-level data or summary statistics. Nature Communications , 12(1), 4192. https://doi.org/10.1038/s41467-021-24485-y
- Zhang, Z., Ersoz, E., Lai, C. - Q., Todhunter, R. J., Tiwari, H. K., Gore, M. A., Bradbury, P. J., Yu, J., Arnett, D. K., Ordovas, J. M., & Buckler, E. S. (2010). Mixed linear model approach adapted for genome-wide association studies. Nature Genetics , 42(4), 355–360. https://doi.org/10.1038/ng.546
- Zhu, H., & Zhou, X. (2020). Statistical methods for SNP heritability estimation and partition: A review. Computational and Structural Biotechnology Journal , 18, 1557–1568. https://doi.org/10.1016/j.csbj.2020.06.011
Citing Literature
Number of times cited according to CrossRef: 2
- Rui Huang, Zhuoying Jin, Donghai Zhang, Lianzheng Li, Jiaxuan Zhou, Liang Xiao, Peng Li, Mengjiao Zhang, Chongde Tian, Wenke Zhang, Leishi Zhong, Mingyang Quan, Rui Zhao, Liang Du, Li‐Jun Liu, Zhonghai Li, Deqiang Zhang, Qingzhang Du, Rare variations within the serine/arginine‐rich splicing factor PtoRSZ21 modulate stomatal size to determine drought tolerance in Populus, New Phytologist, 10.1111/nph.19934, 243 , 5, (1776-1794), (2024).
- Kelvin L. Hull, Matthew P. Greenwood, Melissa Lloyd, Marissa Brink‐Hull, Aletta E. Bester‐van der Merwe, Clint Rhode, Drivers of genomic diversity and phenotypic development in early phases of domestication in Hermetia illucens, Insect Molecular Biology, 10.1111/imb.12940, (2024).

