Methods for the Design and Analysis of Analytical Ultracentrifugation Experiments
Borries Demeler, Borries Demeler
2-dimensional spectrum analysis
AAV capsid quantification
absorbance optics
analytical buoyant-density equilibrium
analytical ultracentrifugation
composition analysis
custom grid method
experimental design
intensity measurements
interaction studies
Monte Carlo method
multi-wavelength analytical ultracentrifugation
parametrically constrained spectrum analysis
sedimentation velocity
solution studies
stoichiometry determination
UltraScan
van Holde–Weischet analysis
Abstract
Analytical ultracentrifugation experiments play an integral role in the solution-phase characterization of biological macromolecules and their interactions. This unit discusses the design of sedimentation velocity and sedimentation equilibrium experiments performed with a Beckman Proteomelab XL-A or XL-I analytical ultracentrifuge and with a Beckman Optima AUC. Instrument settings and experimental design considerations are explained, and strategies for the analysis of experimental data with the UltraScan data analysis software package are presented. Special attention is paid to the strengths and weaknesses of the available detectors, and guidance is provided on how to extract maximum information from analytical ultracentrifugation experiments. © 2024 The Authors. Current Protocols published by Wiley Periodicals LLC.
INTRODUCTION
Many biomedical research projects investigating either fundamental biochemical mechanisms or the molecular basis of diseases focus on the understanding of dynamic interactions between molecules. A century ago, Theodor Svedberg introduced analytical ultracentrifugation (AUC) as a tool to study biopolymers, a breakthrough that was recognized with the Nobel Prize in 1926. Since its introduction, AUC has proven to be a powerful and essential method to study dynamic interactions in the solution phase. Instrumentation and analysis software have seen dramatic improvements, and the range of problems that can be addressed with AUC has been greatly expanded. Experiments can be performed on the Beckman Proteomelab XL-A/XL-I/XL-F instruments, which are equipped with ultraviolet-visible, Rayleigh interference (Giebeler, 1992), or fluorescence detection optics (MacGregor et al., 2004), respectively, but all three instruments have been discontinued by the manufacturer. A replacement instrument without fluorescence optics, the Beckman-Coulter Optima AUC, was introduced in 2017. This instrument offers faster data acquisition with higher radial and wavelength resolution, making it possible to acquire absorbance data for multiple wavelengths in a single experiment (MW-AUC), a technique originally developed using a custom-built instrument with open-source detection optics (Gorbet et al., 2015; Pearson et al., 2015; Pearson et al., 2018).
AUC is an approach for characterizing mixtures of macromolecules in solution by separating them using gravitational force and then measuring their hydrodynamic and thermodynamic properties. It is an indispensable tool in structural biology for the quantitative analysis of macromolecules and macromolecular assemblies. AUC can be used to study mixtures of molecules covering a very large size range (102-108 Da) and under a wide variety of solution conditions where pH, ionic strength, oxidation state, temperature, and concentration of solutes, ligands, and cofactors can be easily modulated to match physiological conditions. Separation is achieved by generating a centrifugal force field to induce sedimentation and diffusion transport and to separate molecules based on their density and buoyant molecular weight, as well as their frictional properties. The optical system detects the partial concentration of individual components in mixtures. Unlike single-molecule techniques such as cryoelectron microscopy, AUC is a bulk observation method that offers high-precision quantification for all molecules in a mixture. In addition to the sedimentation and diffusion coefficients, equilibrium constants and kinetic rate constants can be derived for interacting systems (Demeler et al., 2010). The addition of MW-AUC introduces a spectral separation dimension, enhancing the traditional hydrodynamic separation of AUC experiments. MW-AUC facilitates the characterization of hetero-interactions when individual molecules with unique spectral chromophores can be separated in a MW-AUC analysis. In such systems, it is even possible to determine the molar stoichiometry of assembly (Ahmed et al., 2022; Gabir et al., 2023; Henrickson et al., 2022; Horne et al., 2021; Horne et al., 2020; Johnson et al., 2018; Zhang et al., 2017). By analyzing protein molecules in a physiological solution environment, this technique provides valuable details about dynamic interactions, solution composition, conformation, and oligomerization properties of proteins.
AUC is a first-principle method, considered to be a gold-standard measurement tool for characterizing proteins and other biopolymers in solution. Analysis of AUC data does not require reference standards. As long as the instrument is correctly calibrated, answers obtained can be considered absolute. The versatility of AUC supports a broad range of applications in protein science spanning from the investigation of peptides to that of megadalton complexes, enabling high-resolution measurements for basic research as well as routine quality control applications in the manufacturing of liquid drugs. AUC can offer valuable insights and details when studying proteins. Many questions frequently asked about proteins can often only be answered by AUC. Applications of AUC to protein analysis typically revolve around four basic themes: (1) protein purity and composition analysis, (2) reversible self-association, (3) interactions with different molecules (hetero-interactions), and (4) solvent modulation effects on protein structure and function. General experimental design and analysis considerations for each of these cases are discussed below.
In an AUC experiment, the concentration distributions of analytes in the AUC cell change over time due to sedimentation and diffusion transport, and are typically recorded over several hours and interpreted by the analysis software to derive molecular parameters. This unit will focus on two types of experiments: sedimentation velocity (SV) and analytical buoyant density equilibrium (ABDE) experiments. SV experiments are generally performed in aqueous solutions, where the pH is stabilized by a dilute buffer, and the solution contains a small amount of salts to balance possible charges on the macromolecular analyte (typically 20 to 150 mM). ABDE experiments are performed in highly concentrated density-gradient-forming substances such as cesium chloride (CsCl; ionic) or iodixanol (non-ionic). ABDE experiments have recently been of great interest for the characterization of viral vectors in gene therapy. A related experimental method, sedimentation equilibrium (SE), describes the analyte concentration distribution at the end of the SV experiment, when diffusion and sedimentation transport cancel out and the analyte distribution has reached a point of equilibrium.
Advances in SV data analysis methods make separate SE experiments obsolete, because they can now be analyzed in a global fit together with the approach to equilibrium data, the portion of the experiment typically referred to as an SV experiment. SE experiments by themselves incur many disadvantages, which are further discussed below. ABDE experiments are a form of SE experiment, but provide some unique advantages that deserve special mention. This unit will review the factors important for a successful experimental design, which include sample preparation, selection of the proper optical systems, and diagnostics validating proper instrument functioning, as well as strategies for obtaining data that ensure successful data analysis.
EXPERIMENTAL BACKGROUND
Sedimentation Velocity
For optimum resolution, SV experiments are conducted at a rotor speed that balances the signal obtained from sedimentation and diffusion transport (Gorbet et al., 2018; Williams et al., 2018). SV experiments can be performed in two types of centerpieces: a standard boundary-forming centerpiece or a band-forming centerpiece (also called a Vinograd centerpiece). In a standard boundary-forming centerpiece, 0.46 ml of analyte solution is loaded and sedimented to equilibrium, and the change in concentration is observed as a function of time and radius, by collecting the radial signals of the solution column in multiple scans taken at different times during the experiment. In a band-forming experiment, a small amount of concentrated analyte (2-5 µl) is filled into a reservoir at the top of the sample channel. The sample channel is then filled with a buffer solution that denser than the analyte solution. The higher density is typically achieved by adding heavy water. During acceleration, the analyte solution is forced through a capillary by the centrifugal force and layered on top of the denser buffer solution, forming a narrow lamella, or band , of analyte on top of the buffer solution. The band then sediments and diffuses through the buffer solution according to the hydrodynamic properties of the analytes. For solutions containing multiple, non-interacting solutes, the band quickly broadens into a series of peaks, each peak corresponding to a different analyte. This approach incurs a major drawback: The self-diffusion of light and heavy water during loading at the band interface is very rapid, and current analysis software packages do not take into account the time and radial dependence of the solution density and viscosity change over time induced by the mixing of the light and heavy water columns. Furthermore, the band peaks represent a differential distribution of the analytes, and will rapidly lose signal as they dilute while diffusing and broadening. Because of this, accurate modeling of band sedimentation traces is currently not yet supported, and the potential benefit of higher sedimentation resolution cannot be properly realized. In a standard two-channel centerpiece, all analytes are superimposed and each noninteracting analyte forms a separate, moving boundary. In both cases, the sedimentation and diffusional flow of all solutes, whether interacting or not, is described by the Lamm equation (Eqn. 1; Lamm, 1929):
The Lamm equation is most accurately solved for both non-interacting and reversibly associating systems by the adaptive space-time finite element method (ASTFEM; Cao & Demeler, 2005; Cao & Demeler, 2008). Several powerful fitting methods utilizing the ASTFEM approach for high-resolution data modeling have been implemented on supercomputer architectures within UltraScan (Brookes & Demeler, 2008). The ASTFEM solution of the Lamm equation can model three principal parameters from each analyte contained in the test sample: the sedimentation coefficient (s), the diffusion coefficient (D), and the partial concentration of the analyte (c). The sedimentation coefficient, s , is given by Eqn. 2:
where M is the molecular weight of the analyte, N is Avogadro's number,
where R is the universal gas constant and T the temperature in Kelvin. For reacting systems, equilibrium constants and kinetic rate constants can also be determined under appropriate conditions (Demeler et al., 2010). Because both s and D are determined, the molecular weight of an analyte can also be predicted provided that
Both s and D are inversely proportional to the frictional coefficient, f , which provides shape information. When describing shape derived from an SV experiment, it is important to note that the shape information obtained is degenerate, and a particular s and D combination is not unique for any given macromolecular shape. Consequently, it is customary to express the shape information obtained from an SV experiment in terms of the frictional ratio, k = f/f 0, which is a convenient parameterization of the globularity of the analyte. The frictional ratio compares the frictional coefficient f of the analyte to the minimal frictional coefficient, f 0, of a hypothetical sphere that has the same volume and density as the analyte. Hence, a value of 1.0 for the frictional ratio refers to a perfect spherical shape. For example, spherical nanoparticles can be expected to have frictional ratios near unity, whereas values >1.0 generally indicate asymmetry or extended, nonglobular shapes. Globular proteins typically have f/f 0 values between 1.2 and 1.4, but denatured or intrinsically disordered proteins may have frictional ratios as high as 2.5. Depending on length, frictional ratios of linear DNA fragments, fibrillar aggregates, and filaments can be much higher. Like the molecular weight, the frictional ratio is also dependent on the accurate knowledge of the partial specific volume. The hydrodynamic properties, including frictional ratios for prolate and oblate ellipsoids, as well long rods and spherical particles, can be simulated with various simulation tools in UltraScan. An expression for f/f 0 as a function of s , D , and
where η is the viscosity of the solvent. It is important to note that the frictional ratio is a theoretical construct that requires accurate knowledge of the partial specific volume. Hence, frictional ratio values are only as reliable as the partial specific volume. This is readily noticed when transformations of the measured sedimentation and diffusion coefficients do not necessarily result in an integral molar mass of the protein. Such discrepancies in molar mass are therefore most often due to an error in the partial specific volume, which is also solvent dependent. Another metric commonly derived from SV experiments is the Stokes radius, or hydrodynamic radius, R h. It describes the radius of a sphere that has the same frictional coefficient as the analyte. It is important to note that the Stokes sphere has a larger volume than the actual molecule when the frictional ratio is larger than 1.0. Nevertheless, for spherical molecules the Stokes radius accurately reflects the dimensions of the analyte, including its hydration layer. The Stokes radius can be obtained directly from D by combining it with the Stokes–Einstein relationship as shown in Eqn. 6:
These calculations can be performed with the simulation modules in the UltraScan software (Demeler & Gorbet, 2016), which is available for free download from Github in source code format or as pre-compiled binaries for Linux, Windows, and Mac OSX (Demeler, n.d.).
Sedimentation Equilibrium
The same flow equations governing SV experiments also govern SE experiments. However, in SE experiments the flow is not measured; instead, the equilibrium condition that is established at the end of the velocity experiment is of interest. At this point in the experiment, all net flow in the cell ceases, as sedimentation and diffusion transport exactly cancel. The sedimenting analytes will build up at the bottom of the cell channel, causing a large concentration gradient at the bottom of the cell. This leads to a strong back-diffusion transport that opposes the sedimentation transport. At the end of the experiment, the two transport processes cancel and equilibrium is established. The steepness of the final gradient is proportional to the analyte's buoyant molecular weight and the rotor speed. At equilibrium, the Lamm equation is significantly simplified, as all flow terms cancel, and the equation reduces to an ordinary differential equation, whose solution has an exponential form (Eqn. 7):
where C(r) is the concentration at a radial position in the boundary, C 0 is the concentration at reference point r 0, ω is the angular rotor speed, and b is a baseline concentration.
Typically, short (∼3 mm) solution columns are used in SE experiments, because the length of time required to reach equilibrium is proportional to the height of the solution column. This corresponds to a loading volume of ∼100-120 µl. The time required to reach equilibrium within the noise of the experimental scan can be predicted by simulating the approach of equilibrium using the ASTFEM simulation module in UltraScan. Due to the absence of a net flow in SE experiments, the computational complexity of modeling SE experiments is trivial compared to that of SV experiments. SE experiments can be readily modeled by fitting sums of exponential functions (Eqn. 7) using nonlinear least-squares fitting methods. If the system describes reversibly interacting solutes, multiple terms composed of Eqn. 7 can be used to describe each oligomer or complex in the system, and the fitting parameters, such as the molar mass, can be constrained. For self-associating systems, the molecular weights of oligomeric forms are integral multiples of the monomer molecular weight, and the reference concentrations of each species can be constrained by the equilibrium constants for each association state. Multiple wavelengths, 3-mm centerpieces, and Rayleigh interference optics can be used to extend the concentration range and better characterize reacting systems over a larger concentration range by globally fitting over multiple conditions. Notwithstanding the simplicity of SE modeling, SE experiments have significant limitations in regard to utility. The most serious drawback is related to the dramatically reduced information content compared to SV experiments. In SV experiments, often several hundred distinct observations are fitted simultaneously, but in a SE experiment, the experimental data are obtained from a single scan at the end of the experiment only. Because a shorter column is used, the number of data points that can be fitted is dramatically lower than in an SV experiments. Furthermore, the information content of an exponential function is rapidly exhausted when more than one or two exponentials need to be fitted—sums of exponentials cannot be resolved reliably, as this deconvolution is highly degenerate and ill-conditioned. Another complication comes from the fact that the sample builds up a steep concentration gradient near the bottom of the cell. Therefore, the absorbance near the bottom of the cell typically exceeds the dynamic range of the detector, and is affected by refractive artifacts resulting from the steepness of the gradient. Steep boundaries act as lenses and refract the light from the absorbance optics, distorting the radial position of the observation near the bottom as well. Additional data points near the bottom therefore have to be excluded from the fit, further reducing the available data. The high protein concentration at the bottom of the cell also causes material to aggregate and pellet out due to mass action, constantly disturbing the equilibrium, in the worst case until no material remains visible near the bottom. This violates the conservation of mass requirement, which is one of the boundary conditions for solving the Lamm equation. One possible solution is to lower the rotor speed and to keep the gradient relatively flat, but this all but eliminates the information contained in the SE experiment: Because the concentration distribution at equilibrium is constant, no net flow can be observed, and any shape information is lost. Because the approach to equilibrium data is not taken into account, the information on time-invariant noise contribution is lost, and the entire observed signal becomes time invariant. Hence, numerical time-invariant corrections are not possible. Alternative methods for subtracting time-invariant noise exist (Mortezazadeh & Demeler, 2023), including performing absorbance rather than intensity data collection, but this approach significantly degrades the signal-to-noise ratio of the collected data, and reduces throughput by requiring the second channel in each cell to be used as a buffer blank. Because of these downsides, traditional absorbance measurements cannot be recommended (Demeler, 2010). Taking those negatives together, due to their low resolution and reduced information content, SE experiments have been largely replaced by SV experiments (Demeler et al., 2010).
Analytical Buoyant-Density Equilibrium Experiments
Despite the obvious drawbacks of standard SE experiments, there are exceptions. Analytical buoyant-density equilibrium (ABDE) experiments are a form of equilibrium experiment that rely on a density-gradient-forming material to establish equilibrium, separating all analytes based on their buoyant density. Analytes with different buoyant densities form peaks at radial positions where the density of the gradient material is identical to the buoyant density of the analyte. Because the width of the peak formed at equilibrium is proportional to the diffusion coefficient of the analyte, large molecules, such as most viruses and bacteriophages, form very sharp peaks, and only very small amounts of analyte are needed to achieve baseline separation between the peaks while remaining within the dynamic range of the detector. This means that the density resolution of ABDE experiments is very high for such systems and the sample requirements are very low, which is important for expensive samples that are available only in limited amounts (Henrickson et al., 2023). For example, this can be very useful for the analysis of viral vectors (Henrickson et al., 2023; Richter et al., 2023; Savelyev et al., 2023; Sternisha et al., 2023) where the degree of capsid loading needs to be quantified. Because the densities of proteins and nucleic acids are quite different, the ABDE approach provides a high degree of resolution between empty, partially, and fully loaded capsids. The density profile and resolution obtained in ABDE experiments can be easily modulated by changing the rotor speed and by adjusting the loading concentration of the density-gradient-forming material (Henrickson et al., 2023). There are two types of density-gradient-forming materials available: ionic (CsCl, Cs2SO4) and non-ionic (Nycodenz, metrizamide, iodixanol). The observed density position in each of these materials varies greatly depending on the charge of the analyte. Highly charged molecules appear to be much denser in ionic as compared to non-ionic gradient-forming materials, because their hydration is much greater in non-ionic materials. On the other hand, in cesium-containing gradients, anionic molecules such as nucleic acids bind cesium ions, increasing their apparent density. This effect can be exploited to fine-tune the resolution of the ABDE experiment. One important limitation is the optical density of most of the non-ionic density-gradient-forming materials in the UV. Because of their strong background absorbance and refractive index, these materials are best suited for use with fluorescently labeled molecules analyzed with the fluorescence optical system. Optically pure CsCl is a preferred material to use in UV absorbance optics, where it is largely transparent. The refractive index of CsCl is still significant, but the refractive effects caused by the gradient shape can be mitigated by using 3-mm centerpieces, which reduces the pathlength and also further reduces the required sample volume. ABDE experiments can also be performed as MW-AUC experiments, further extending their information content (Henrickson et al., 2023).
Detectors
A number of detectors are currently available for the Beckman analytical ultracentrifuge. UV-visible absorbance and Rayleigh interference detectors are commercially available from Beckman-Coulter (Indianapolis, Indiana; http://www.beckman-coulter.com), and a limited number of instruments equipped with a fluorescence detector built by Aviv Biomedical are still in operation. A multi-wavelength absorbance detector has been developed by H. Cölfen (Pearson et al., 2018; Strauss et al., 2008), and construction plans are freely available from the authors (Cölfen et al., n.d.). A commercial retrofit version for the Beckman XL-100 and Proteomelab instruments is available from Nanolytics (Potsdam, Germany; https://www.nanolytics.com). The latest instrument available from Beckman-Coulter, the Optima AUC, also supports multi-wavelength data acquisition at up to 100 wavelengths per experiment (when using UltraScan for data acquisition). Each detector has distinct advantages for selected applications and provides complementary information. The capabilities, pros, and cons of each detector deserve a detailed discussion, which is provided below (for a technical discussion of the absorbance and interference optical systems, see Laue, 1996). MW-AUC experiments from the two available detector systems and their pros and cons are discussed in detail by Henrickson et al. (2022).
Absorbance Optics
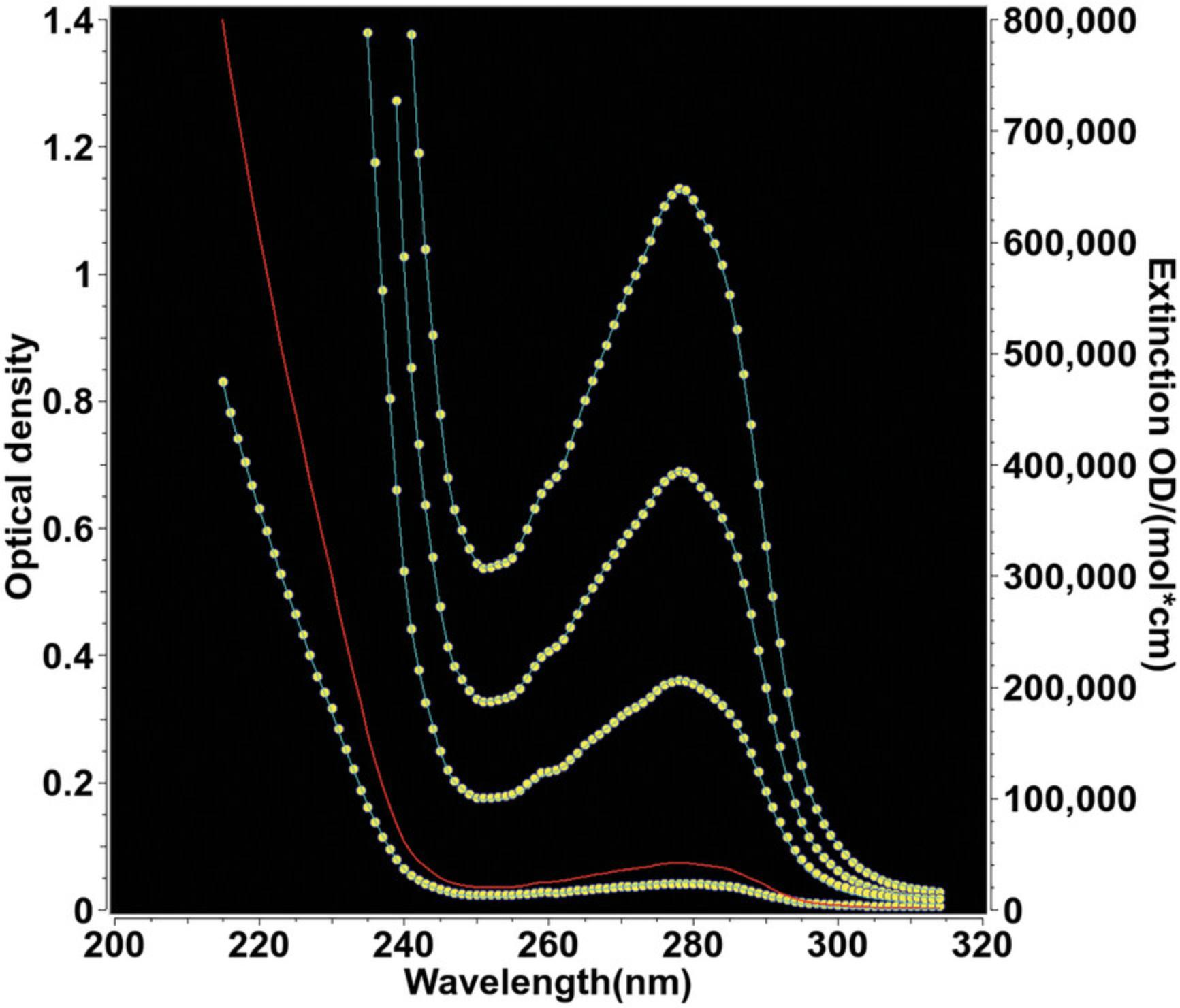
The optical system most widely used in analytical ultracentrifuges is the absorbance optical system. This permits the analysis of protein and DNA samples under dilute conditions, in which their hydrodynamic transport is generally unimpeded by concentration-dependent nonideality effects. The strong extinction of DNA and protein samples in the UV range, coupled with the relatively high intensity of the xenon flash lamp in the UV range, make absorbance and intensity measurements a very sensitive method for protein and DNA measurements. However, UV and visible absorbance or intensity measurements can only be performed in non- or low-absorbing buffer systems. This restricts the use of the absorbance optics to a subset of additives and buffer systems and to a subset of wavelengths. If macromolecules are sedimented in the presence of absorbing additives, such as nucleotides, reductants, and other absorbing drugs, or at wavelengths where the buffer system itself absorbs, the total absorbance of solutes and buffer can easily exceed the dynamic range of the UV/visible absorbance system, and a Rayleigh interference or fluorescence intensity detector may be more appropriate. The dynamic range of the detector is defined as the optical density range over which a linear signal is returned: e.g., if the concentration is doubled, the detector signal should double as well. Figure 1 shows the absorbance patterns of popular reductants; absorbance spectra for popular buffer systems can be found online (see Iranzo & Kumar, 2009, which outlines several buffer systems that are suitable for measurement in the far UV). For protein measurements at 280 nm, the use of tris(2-carboxyethyl)phosphine (TCEP) is recommended when a reductant is required due to the low UV absorbance of TCEP. Other reductants, most notably dithiothreitol (DTT) and β-mercaptoethanol (BME), should be avoided, even at low concentration, because their UV absorbance changes in different oxidation states, which causes unpredictable baseline changes and absorbance changes that cannot be modeled. When nucleotides or other absorbing drugs are added to a buffer, it is important to review the extinction spectra of the buffer additives and the analyte separately. Comparing the two spectra will be helpful to find a wavelength that maximizes the absorbance of the analyte and minimizes the buffer's background absorbance.
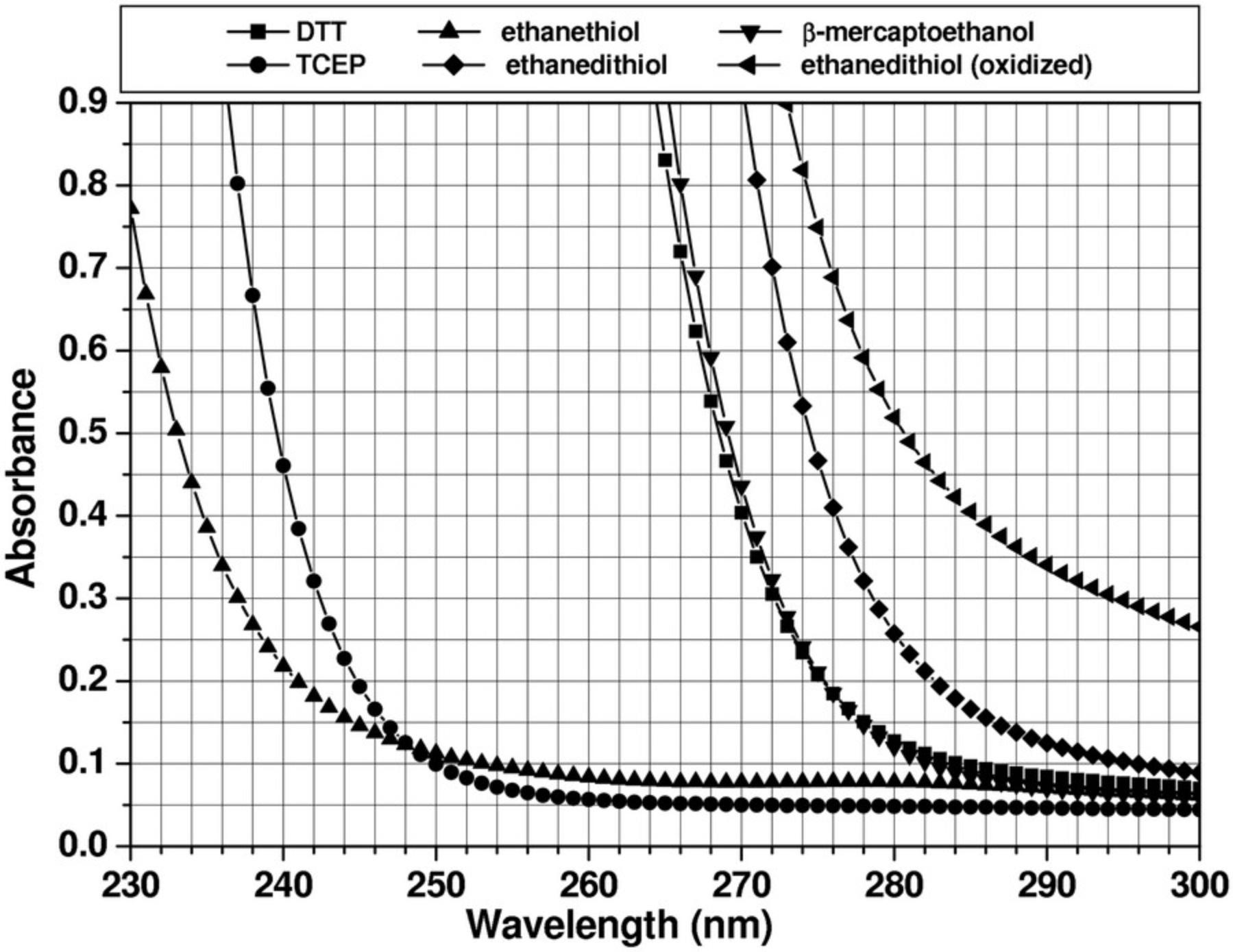
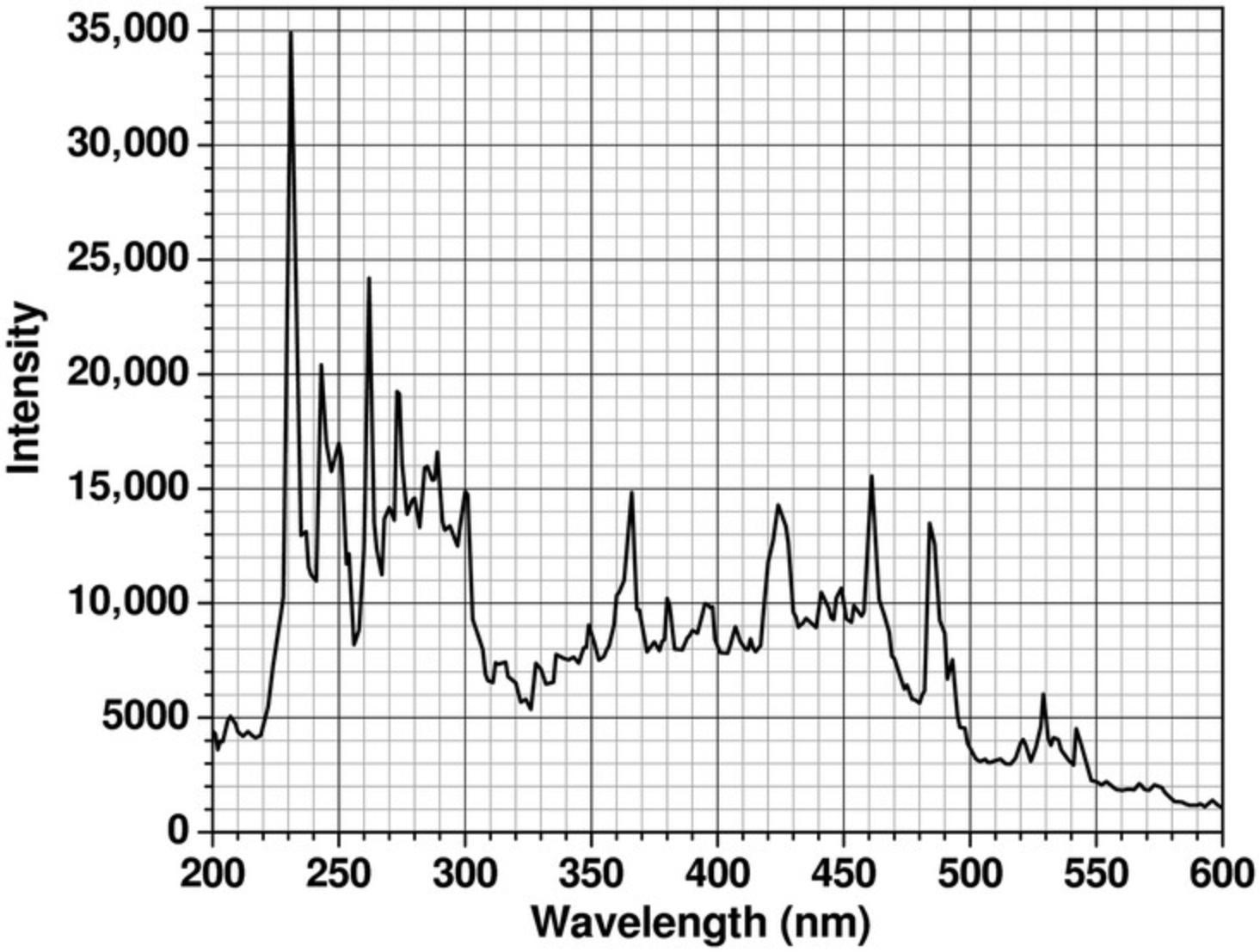
The dynamic range of the absorbance optics is also dependent on the intensity of the lamp, which varies greatly with wavelength (see Fig. 2). As a rule of thumb, the sum of buffer absorbance and analytes present in the system (measured against distilled water) should always be <1.5 optical density units (OD) at wavelengths that produce a high intensity (e.g., 230 nm) and ≤1.0 OD at wavelengths at which emission intensity is reduced. Otherwise, nonlinearity in the measurement and excessive noise will reduce the accuracy of the measurement. Furthermore, the xenon flash lamp inside the XL-A instrument tends to collect dirt on the lamp window over time, which further reduces light intensity. In the Optima AUC, mirrors in the absorbance system tend to degrade over time due to the high-intensity UV emission in the xenon lamp. Therefore, the lamp intensity should be routinely checked to ensure that the optical components are in good shape. A clean XL-A xenon flash lamp will produce an emission spectrum similar to the spectrum shown in Figure 2, although the absolute emission peak intensities may vary between instruments. If buffer absorbance is minimal at lower wavelengths, protein concentration can be reduced significantly by taking advantage of the strong peptide bond absorbance present in each protein or peptide in the lower UV range. Depending on the abundance of aromatic residues in the protein, the molar extinction coefficients between 215 and 230 nm can exceed the molar extinction around 280 nm by an order of magnitude or more.
The UV-visible detector collects data in intensity mode by recording the intensity of the transmitted light at each radial position. However, to obtain a reading that is proportional to concentration, data from AUC experiments must be converted to absorbance data. To do this, the intensity of light recorded for the sample, I S, must be converted to an absorbance value, A , using a reference intensity, I R, by applying the conversion shown in Eqn. 8:
Both instruments provide a software-based conversion option to generate absorbance data by applying Eqn. 8 for each radial point, obtaining the I R value from a separate scan of a buffer or water reference channel. As discussed earlier (Demeler, 2010), this approach has several drawbacks. In intensity mode, the intensity of the light passing through each channel is independently recorded, accumulating separate stochastic and time-invariant noise signals (Kar et al., 2000; Schuck & Demeler, 1999). During the conversion performed in Eqn. 8, the stochastic noise in the resulting absorbance data is amplified by a factor of √2 ≈ 1.414. This is a significant increase in noise that should be avoided (Demeler, 2010). In addition, reference data require a separate cell channel, which cannot be used for a sample, reducing the throughput of the experiment. Optical components contribute time-invariant noise, which varies as a function of radius and can only partially be eliminated by a point-by-point absorbance conversion, because the time-invariant noise contributions originating from the cell windows differ for separate channels, leaving residual time-invariant noise unaccounted for. The entirety of each channel's time-invariant noise contribution in SV experiments can be effectively eliminated with a numerical approach during data fitting, obviating the need for a reference channel scan (Demeler, 2010; Schuck & Demeler, 1999). Nevertheless, an I R value is still required for the conversion to absorbance data. In UltraScan, intensity data are converted to absorbance data by utilizing the intensity value obtained by averaging a few points from the intensity measured in the air region above the meniscus from each scan, where no absorbance should be present.
To better understand the reason for the difference in data quality between intensity and absorbance data, the source of various noise signals merits further discussion. In an absorbance experiment, the light passes through several optical components, including the lamp window, focusing lenses, and the monochromator, followed by the upper cell window, the solution column, the lower cell window, and additional focusing optics in the slit assembly, before finally reaching the photomultiplier window. Each light flash is independently imaged and collected as a single intensity data point. In an absorbance experiment, each radial position is measured twice, once through the sample sector and once through the reference sector. Each observed intensity measurement I obs is convoluted with a number of noise sources, which can be summarized as shown in Eqn. 9:
where I 0 is the intensity of the lamp, N ri is the radially invariant noise component, N ti,window is the time-invariant noise component contributed by the windows of the AUC cell, N ti,other is the time-invariant noise component contributed by all other optical components, N s is the stochastic noise component contributed by the flash lamp and electronics, and S is the intensity loss due to absorbance by the sample, with contributions by both buffer and analyte(s). The radially invariant noise contributions arise from changes in lamp intensity over time (e.g., through slow formation of a deposit on the lamp window), leading to slight shifts in the baseline absorbance of each scan, or, in the case of interference optics, from slight changes in optical pathlength due to heating and cooling cycles in the instrument. This noise will add a constant offset to the baseline of each scan. Time-invariant noise contributions arise from imperfections of any optical component that light passes through. The largest amplitude of time-invariant noise originates from the response variability of the photomultiplier tube as a function of radius and wavelength. Additional time-invariant noise will result from dirt or scratches on a cell window. Like a fingerprint on a camera lens, this noise will not vary over time and will produce the same invariant noise contribution in every scan taken. Fortunately, time-invariant and radially invariant noise contributions can be removed algebraically with algorithms implemented in UltraScan (Schuck & Demeler, 1999). Although all noise contributions are additive, it is important to note that the time-invariant noise contributions from the upper and lower cell windows are different for the sample and reference sector (e.g., a scratch on the window may be in a slightly different position on the reference sector than in the sample sector).
Although time-invariant noise contributions from optical components other than the cell window are effectively removed from the resulting data by virtue of the reference subtraction when collecting data in absorbance mode, a small amount of time-invariant noise resulting from the difference in cell window noise remains in the data. This is particularly troublesome in cases where very narrow, high-amplitude time-invariant noise signals distort the sample signal, as with small scratches on cell windows, because the precision of the radial scanning stepping motor is too low to always detect such narrow distortions at the same radial position. As a consequence, such distortions are reported at slightly different radial values and are no longer truly time invariant. In addition, each radial point from each sector has a unique time-dependent stochastic noise signal associated with itself, which is different for the corresponding radial observations from reference and sample sector. During the subtraction of the reference signal from the corresponding sample signal, the stochastic noise contributions and the (random) differences in the time-invariant noise signals from the upper and lower windows are convoluted. Whenever stochastic noise signals from two observations are convoluted, the total noise signal increases, on average, by a factor of √2, which is undesirable.
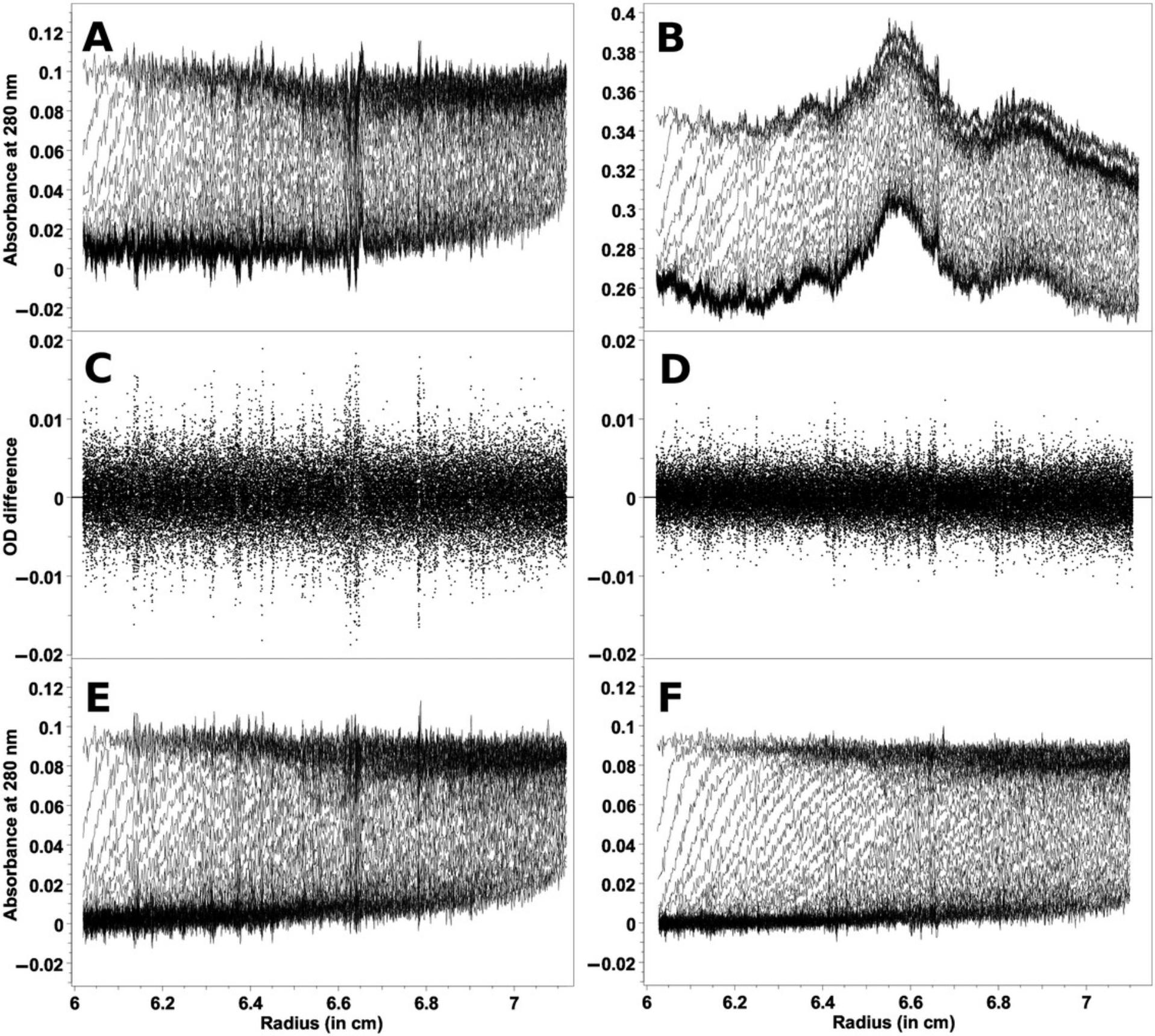
When intensity measurements are taken, all time-invariant noise contributions are additive and can be represented in a single time-invariant noise signal. The improvement in stochastic noise by a factor of √2 for intensity SV experiments compared to absorbance SV experiments is demonstrated in Figure 3, which shows a comparison between measurements made of the same sample in both intensity and absorbance modes. Here, a sedimentation velocity experiment was performed in absorbance mode, and then the same sample was resuspended and measured in intensity mode, using the same cell and run conditions. Figure 3A shows the data obtained from the absorbance measurement, and Figure 3B shows the intensity data. On first glance, the intensity data appear to be significantly worse, because the time-invariant noise contributions from the photomultiplier tube are quite significant. The time-invariant noise contributions calculated algebraically by UltraScan for both experiments are compared in Figure 4. In the absorbance experiment (Fig. 4A), the majority of the time-invariant noise is eliminated through subtraction of the reference channel, and the remainder is hence due solely to differences between the cell windows. However, the significant time-invariant noise contribution shown in the intensity data (Fig. 4B) is readily removed by the same algorithm in UltraScan, leaving only radially invariant and stochastic noise. Figure 3C shows the stochastic noise residuals resulting from the two-dimensional spectrum analysis (2DSA; Brookes et al., 2010; Kim et al., 2018) fit of the absorbance data, and Figure 3D shows the residuals for the intensity data when analyzed with identical analysis settings. Panels E and F in Figure 3 show the noise-corrected data obtained from the absorbance and intensity experiments. It is clearly evident that the quality of data obtained when measuring in intensity mode is significantly better than the quality of data obtained in absorbance mode. This is reflected in the residual mean square deviation (RMSD) of the fit, which differs approximately by a factor of √2, as predicted by statistical theory (3.5543 × 10–3 for absorbance mode and 2.3705 × 10–3 for intensity mode).
Rayleigh Interference Optics
The interference optics measure the refractive index difference between a sample and a reference cell. The fringe pattern generated by the refractive index differences are converted by a fast Fourier transform into concentration profiles, which can then be evaluated by standard methods. Although it is less sensitive than absorbance optics, there are several advantages to interference optics: First, sedimentation can be performed in the presence of absorbing buffer components. Second, the dynamic range of the interference optics is much higher than the dynamic range of the absorbance optics. This makes it ideal for the measurement of more concentrated solutions. Finally, the radial and temporal data density is much higher than in the absorbance optics. It should be noted that the sample should not absorb between 660 and 675 nm, which are the wavelengths of the lasers used in the Optima AUC and the Proteomelab XLI, respectively. Data scans can be acquired approximately every 10 s in the Proteomelab XLI (5 s in the Optima AUC), and the radial resolution of interference data is ∼7 μm versus ∼30 μm in the Proteomelab XLA and 10 μm in the Optima AUC.
When performing interference experiments, it is important to note that generally all components dissolved in the solution contribute to the interference pattern, including non-absorbing salts and buffer components. At higher rotor speeds, even small-molecular-weight buffer components can sediment or form gradients, contributing their own sedimentation and diffusion signals to that from the analyte(s). To eliminate the superposition of buffer component signals onto the analyte signals, the buffer can be filled into the reference cell, with the menisci from both channels matched as closely as possible to avoid different buffer sedimentation signals between channels. A meniscus-matching centerpiece can be used to equilibrate the sample and reference solution column heights through a small capillary at the bottom of the cell between the two channels. In addition to matched menisci, this approach requires that the refracting buffer components be present at the same concentration in the sample and reference channels. A match is best achieved by thorough dialysis, and using the dialysis buffer or the column buffer from a column chromatography experiment in the reference channel. Alternatively, it is possible to simply use purified water in the reference cell, and to load the reference channel with a 5- to 10-μl larger volume than the sample channel. In that case, UltraScan can model the sedimentation of the buffer components in addition to the analyte(s) of interest, and separate the hydrodynamic signals from each component in the mixture. In such a setup, there is no danger from buffer components sedimenting under mismatched menisci, which would distort the results by overlaying an unpredictable difference spectrum of the buffer components on top of the analyte signal.
For best results, interference experiments should employ sapphire windows. Unlike sapphire windows, standard quartz windows tend to have a strong heterogeneity of refractive index. Furthermore, the refractive index properties seem to change with centrifugal forces acting on the windows. This prevents these noise signals from being treated as pure time-independent signals. Another complication can occur with improperly focused optics. In order to minimize Wiener skewing effects, the optics should be focused by a service engineer, and steep gradients should be avoided by using a lower rotor speed and by using longer solution columns.
Fluorescence Optics
Fluorescence optics offer superior sensitivity and exquisite selectivity (MacGregor et al., 2004), allowing samples to be observed in impure or absorbing liquids. Some samples can be measured reliably at low-nanomolar concentrations. As in interference optics, the dynamic range is much larger than in absorbance optics; however, the user has to manually adjust gain settings to optimally exploit the dynamic range. All molecules must be labeled with fluorescent tags whose excitation range coincides with the excitation laser's wavelength (typically 488 nm). Tags such as Alexa488, SybrGreen (for dsDNA), fluorescein, and other fluorescein-based tags can be used. Proteins can also be fused to green or yellow fluorescent protein, providing intrinsic fluorescence. Emission intensity is filtered to only allow signals >500 nm to be observed. The optical setup employs a confocal microscope to measure the emission of the fluorophore at each radial position, focused a few millimeters below the top cell window to avoid inner filter effects. A counterbalance filled with fluorescein is required in each run to obtain a radial calibration, and scans are collected for all cells and channels simultaneously, enhancing throughput. Reference channels can be filled with samples as well; a buffer reference is not required. Samples must be degassed prior to cell loading, and the addition of a non-tagged carrier protein such as ovalbumin at a concentration of 0.1 mg/ml is recommended, especially for samples with proteins at very low concentration. The great selectivity in fluorescence optics permits the analysis of intrinsically labeled proteins without purification in whole-cell extract suspensions, blood serum (Kingsbury et al., 2008; Kroe & Laue, 2009), or other physiological solutions.
EXPERIMENTAL DESIGN
Proper experimental design is a crucial step in a successful AUC experiment, and attention needs to be paid not only to the run conditions but also to the condition of the instrument. A series of instrument diagnostics and sample preparation steps will help to obtain optimal data for analysis.
Instrument Diagnostics
A successful experiment clearly depends on a properly calibrated and well-functioning instrument. The Beckman XL-A/I instruments do require periodic maintenance and calibration. The following tests should be performed to ensure that the instrument is in optimal condition. For all detectors, a careful calibration of the optical focus is essential. This should be performed by a Beckman service representative. The user can regularly perform several other diagnostics, including the radial calibration of the instrument; guidelines for these procedures are available in the instrument manual. For absorbance optics, the intensity of the lamp should be routinely checked. A wavelength intensity scan of an empty rotor hole performed at 6.5 cm should produce the intensity pattern shown in Figure 2. An intensity scan across an empty rotor hole at 230 nm from 5.8 to 7.2 cm should produce a pattern that does not vary more than 10% across the cell. If the intensity at 230 nm is low, or varies more than 10%, either the lamp (in the Proteomelab XLA) needs to be cleaned, or the slit assembly and other optical components need to be cleaned or serviced. An intensity pattern displaying a peak intensity in the middle of the cell, and dropping off symmetrically on either end of the cell, should be seen. If the pattern shows a noticeable intensity trough in the center, the photomultiplier tube may need to be replaced. If the intensity peak is not near the center of the cell, or there is a sharp drop of intensity on either side, the photomultiplier tube may need to be realigned. Reproducibility of the wavelength should be within ±2 nm in the Proteomelab XLA (0.5 nm in the Optima AUC); several wavelength intensity scans should produce plots that show congruent emission peaks at all wavelengths. The Optima AUC also offers the ability to perform multi-wavelength experiments, but due to the use of lens-based optics, chromatic aberration can lead to different focus positions, as well as radial offsets that differ at different wavelengths. UltraScan offers the ability to collect a chromatic aberration profile and to upload this profile into the UltraScan LIMS database, to automatically adjust for chromatic aberration by adding or subtracting an appropriate radial increment for each wavelength that will align all wavelengths to record the same radial position as the radial calibration performed at 250 nm. Details of this procedure can be found at: https://resources.aucsolutions.com/chromatic_aberration_calibration.php.
Another issue that frequently needs to be checked with the XL-A optics is the radial reproducibility. In some cases, dirt, oil, and other contaminants can impede the smooth operation of the slit assembly and cause irregular radial positioning. This problem is easily detected when the meniscus position of a high-speed absorbance experiment varies from scan to scan. This problem is corrected by thoroughly cleaning the slit assembly, or, if necessary, replacing the slit motor.
Sample Preparation and Sample Concentration
The flexibility introduced by a choice of several optical detectors permits the analysis of proteins under a very large range of analyte concentrations, buffer pH, and ionic strength and in the presence of detergents, nucleotides, reductants, and other additives. In general, the most reliable results are obtained by analyzing the samples under dilute conditions, which minimize concentration-dependent hydrodynamic and thermodynamic nonideality. It is important to realize that the methods implemented during routine fitting of experimental data (see Eqn. 1) consider ideal solutes only. Such ideal solutes do not exhibit changes in their sedimentation and diffusion coefficients as a function of concentration, pressure, or time. However, many factors can lead to nonideal transport, but fortunately, methods exist to diagnose the presence of nonideality, and appropriate experimental design strategies avoid nonideal sedimentation and diffusion transport for the vast majority of routine protein characterization experiments. Protein concentrations of <1.0 optical density units at 230 nm are generally dilute enough to avoid concentration-dependent nonideality contributions. Use of wavelengths <250 nm excludes the use of many additives and virtually all reductants (see Fig. 1). If in doubt, the absorbance spectrum of the additive should be measured against that of water, to adjust the concentration of the additive such that the total sample and buffer absorbance does not exceed the dynamic range. For charged molecules, some counter-ions should be present in the buffer (e.g., a minimum of 20 mM ionic strength is recommended) to reduce the effect of charges on the analyte, which may contribute to concentration-dependent nonideality. Gradient-forming buffer components should be avoided in high-speed experiments. In principle, molecules as small as a few hundred Daltons (such as salts, glycerol, and sucrose) can produce density and viscosity gradients at higher speeds, which will affect the sedimentation and diffusion coefficients by constantly changing the local density and viscosity in the solution during the course of the experiment. Reducing the speed, or lowering the concentration of the gradient-forming components, will reduce the gradient to negligible levels. If in doubt, a velocity experiment can be performed with the buffer solution measured at the desired speed against water using interference optics. This experiment will reveal the approach to equilibrium gradient as a concentration profile of the buffer components, from which the density and viscosity differences at the top and at the bottom of the cell can be estimated. These values can be entered into the UltraScan hydrodynamic parameter simulation routine and the effect on the change in s and D can be estimated.
In terms of the physical setup, the condition of the centerpieces is very important; they should be free of scratches, which can cause leaks, turbulence, and convection of the solutes, and the use of scratch-free windows is recommended. A proper alignment of the cell in the rotor hole is also critical. Misaligned cells also cause turbulence and convection, which distort the sedimentation profiles. Proper alignment within 0.1 degrees can be achieved with a commercially available cell alignment tool (http://www.nanolytics.com/). For the same reason, worn-out cell housings and loose-fitting or damaged centerpieces should not be used. Inspect the centerpiece for scratches or distortions of the septum. Such distortions can occur if the cell leaks in one channel, causing a hydrostatic pressure differential across the septum. To prevent such damage, the first few scans of any experiments should be actively monitored for cell leaks by comparing the meniscus position from the first few scans. If a leak occurs, the machine should be stopped immediately to prevent damage to the centerpiece. For velocity experiments, intensity experiments can take advantage of the reference channel to measure a second sample. However, in the Proteomelab XLA, the reference channel can only be used for low-concentration samples (<0.5 OD) to avoid resetting the photomultiplier tube gain setting mid-run. No such restrictions exist for the Optima AUC, or for the sample channel in either instrument. An excellent use of the two channels in each cell is to establish the presence of mass actions of proteins. In the Proteomelab XLA, the same sample can be measured at three-fold different concentrations (0.3 OD in the reference channel and 0.9 OD in the sample channel at the same wavelength). In the Optima AUC, the difference in concentration can be maximized by measuring using different wavelengths where the extinction coefficients of the analyte differ greatly. Measuring the same protein at multiple concentrations provides an assay for reversible protein oligomerization.
An important application for AUC experiments is the measurement of equilibrium constants for self-associating systems (Demeler et al., 2010). In dynamic reactions such as monomer-polymer oligomerizations, the most reliable answers are obtained when a broad concentration range can be analyzed that contributes sufficient signal from the monomer, as well as the oligomeric forms. Due to mass-action laws, the monomer species will be emphasized at low concentrations, whereas the signal from the oligomer will be predominant at high concentrations. When measuring equilibrium coefficients by SV experiments, it is advisable to measure at a concentration near the putative k D. Measurement at different wavelengths broadens the concentration range, and if the absorbance profile of the buffer is suitable, measurements at loading concentrations of 0.3-0.7 OD at between 215 and 295 nm will access the largest concentration range for proteins. Measurements of two protein concentrations confirm that the sample does not contain any aggregates or contaminants, and identify the presence of reversible association by comparison of the sedimentation coefficient distributions from each concentration. If these concentrations overlay, the sample is non-interacting or is far from the equilibrium constant concentration (Demeler et al., 1997). It is important to note that the precision of the monochromator in the Proteomelab XLA is not sufficient to allow changing the wavelength within a run. Due to variable extinction coefficients of proteins at different wavelengths, a failure to reset to the exact wavelength will cause apparent concentration nonlinearities within an experiment, rendering the data useless. This is particularly of concern in the regions where the absorbance profile of the analyte changes rapidly, for proteins between 250 and 220 nm. When performing MW-AUC experiments on mixtures with multiple chromophores, concentrations should provide approximately equal absorbances for each unique chromophore in order to balance the signal concentration when deconvoluting the spectral contributors. To achieve the desired mixing ratios, observed wavelength ranges should be carefully considered to maximize orthogonality as well as total signal from each molecule. Additional design considerations for MW-AUC experiments are discussed by Henrickson et al. (2022).
Speed Selection
The rotor speed selection is critical for the success of an AUC experiment, and several factors need to be considered. A high rotor speed produces the best resolution when performing composition analysis and when the accuracy of sedimentation coefficients and partial concentrations is critical. However, at high rotor speed, all solutes will sediment rather quickly, with little time to diffuse. This will reduce the signal observed for the diffusion coefficient, which provides frictional information critical for shape and molecular weight calculations (Gorbet et al., 2018; Williams et al., 2018). To obtain the best signal for both sedimentation and diffusion coefficients, UltraScan offers global fitting of multi-speed experiments, which combine the strong diffusion signal from the slow experiment with the strong sedimentation and partial concentration signal from the high-speed experiment into a single solution (Ranasinghe et al., 2023). From such globally fitted data, molecular weight, partial specific volumes, or frictional properties can be obtained (Demeler et al., 2014). For single-speed SV experiments, the speed should be chosen to represent a good compromise between high- and low-speed sedimentation. This can best be achieved by modeling the solutes in the “Finite Element Simulation (ASTFEM)” implemented in UltraScan. A speed should be selected that results in a minimum of 40 to 60 scans that result in complete pelleting of the solute. For experiments involving multiple cells, the scanning time of each cell needs to be taken into account when selecting the proper speed. For samples with great heterogeneity, experiments performed at multiple speeds and globally fitted will provide the best resolution. For ABDE experiments, the highest possible speed will result in the greatest density difference of the gradient material, and therefore provide the largest dynamic range for separating particles with different buoyant densities. For viral vector characterization of empty and partially and fully loaded viral capsids, a CsCl concentration of 1.36 g/ml and a centrifugation speed of 60,000 rpm will resolve all three capsid forms as separate peaks in a single experiment. Slower speeds, and variations in the concentration and type of gradient-forming material, can be used to optimize and focus a particular density range, providing additional resolution in a narrower region of the density profile (Henrickson et al., 2023).
Loading Volume and Column Height
For all experiments, it is advantageous to maximize the column height in order to increase the information content of the data. A longer column allows the sample to sediment over a longer distance, which improves resolution. In addition, a longer column results in more data points, and therefore improves the signal-to-noise ratio. However, a small air bubble at the top of the solution column is necessary for meniscus identification, which is a required boundary condition for the finite element solutions of the Lamm equation. In addition, a short scan region capturing the air above the meniscus is required to obtain the reference intensity for the conversion to absorbance data. A loading volume of 450-460 µl in 12-mm centerpieces (110-120 µl for 3-mm centerpieces) is recommended for all experiments. For interference optics, the air region is required for the baseline alignment of all scans (Schuck & Demeler, 1999). In ABDE experiments, a longer column height provides the largest dynamic density range, but it also requires longer equilibration times.
Determination of a Molar Extinction Coefficient Profile
A key property of proteins to be measured by AUC is their tendency to self-associate, and the k D of this interaction. To probe for the k D concentration, multiple concentrations of the oligomerizing molecule must be evaluated. This requires precise knowledge of the molar extinction coefficients at different wavelengths, because most biopolymers have chromophores in different regions of the UV/visible wavelength range, depending on their composition or co-factors. For example, in proteins, the amino acid side chains tryptophan, tyrosine, and phenylalanine, as well as cysteine disulfide bonds, contribute to a protein's absorbance between 240 and 300 nm, and below this range a strong absorbance band originates from the peptide bond. In addition, a protein may absorb in the visible range (including heme and fluorescent proteins), while DNA absorbs strongly around 260 nm. Macromolecular conformation and solvent conditions further contribute to the detailed and variable shape of each molecule's absorbance pattern. Therefore, each molecule should first be measured by UV/visible spectroscopy in the experimental buffer to determine precise molar extinction coefficients at all wavelengths to be used for the AUC experiment. Intrinsic extinction profiles are determined by performing a dilution series of the target molecule using the same buffer into which the protein was dialyzed or eluted. This buffer should also be used to blank the spectrophotometer in case of any background absorbance. The absorbance of the buffer should be checked against that of water to assure that the total absorbance, including the molecule of interest, does not exceed the dynamic range of the detector. Multiple dilutions are scanned over the wavelength range of interest and are then globally fitted to an intrinsic extinction spectrum using the UltraScan Spectrum Fitter module. The range of dilutions should cover the entire wavelength range with an absorbance that includes an optical density of 0.4-0.6 OD for at least one dilution across the spectrum, and at least three dilutions of the protein should be used to cover the entire wavelength range. If a molar extinction coefficient is available for at least one wavelength, this value can then be used to normalize the entire absorbance profile to the known value, which then provides the molar extinction coefficients for all wavelengths in the fit. An example of such a global fit is shown in Figure 5 for bovine serum albumin.
Data Acquisition and Instrument Settings
An AUC experimental design requires the user to select multiple parameters for an experiment. They include rotor speed, temperature, number of scans, and the duration of the experiment. For the UV/visible detector, wavelengths and radial scan ranges need to be selected, and fluorescence detection also requires a focus setting for each channel and a photomultiplier gain setting, which should be set to maintain the dynamic range of the detector (4000 counts maximum) over the entire fluorescence emission range. For the older instruments, slower scanning times may place a constraint on the available data during an experiment, and programming a nonzero delay between scans is counterproductive; the delay should always be set to zero to maximize the scan count for SV experiments. In general, more data translates into an improved signal-to-noise ratio, but the gain is limited to the region where boundary movement is observed. Once the sample has sedimented completely, inclusion of additional baseline scans is not useful and should be avoided, although data acquisition should not be aborted before the boundary has moved completely to the bottom of the cell, or has reached equilibrium. Similarly, it is best practice to exclude any scans at the beginning of the experiment that have steep boundaries, which could result in measurable refractive artifacts. Nevertheless, early scans should be collected to aid in the detection of cell leaks by active monitoring of the meniscus positions early in the experiment. Radial resolution for the Proteomelab XLA is variable; a setting of 0.003 cm is a good compromise between fast scanning and radial resolution of the instrument. For slowly sedimenting proteins, a smaller increment (0.001 cm) can be chosen, but a regular spacing of 0.001 cm will not be observed in the Proteomelab instruments, because it uses a servo motor to move the slit assembly, unlike the digital stepping motor employed in the Optima AUC, which does provide a regular 0.001-cm increment by default. For ABDE experiments, the approach to equilibrium scans are only useful to show when equilibrium is reached, and a single scan at equilibrium provides the desired information. For fastest results, any multi-speed ABDE experiments should be first performed at the highest speed; once equilibrium is reached, the speed should be reduced to the next slower speed step.
Although multi-wavelength experiments are possible with the Optima AUC, the wavelength setting should never be changed during an experiment for runs performed on the Proteomelab XLA. The reason is the lack of precision of the monochromator, which also uses a servo to reset to the selected wavelength. Even small changes occurring during resetting of the wavelength can cause major changes in extinction, especially at wavelengths near the absorbance shoulder (e.g., 230 nm in proteins).
Data Management
The UltraScan software includes a database back end that provides convenient tools to support multi-user facilities and track projects from multiple investigators. This system is used to manage experimental data and analysis results and to store supporting information such as buffer composition, protein and nucleic acid sequences, gel images, absorbance spectra, and experimental designs, as well as other ancillary information, that are associated with the experimental data. The stored protein sequences are used to estimate molecular weight, partial specific volume, and extinction coefficients at 280 nm, and the buffer composition information is used to calculate buffer density and viscosity. This system is collectively called the UltraScan Laboratory Information Management System (USLIMS) and provides high-performance computing access to institutions in the United States, Canada, Asia, Australia, and Europe. It also functions as a collaborative tool for exchanging experimental information. It can be accessed both through UltraScan and through the UltraScan Science Gateway, a web portal offered by the National Science Foundation's Computer and Information Science and Engineering division (formerly Teragrid, then XSEDE, and now ACCESS). These resources allow users to manage the compute-intensive analysis methods offered by UltraScan on remote supercomputers, using cloud storage (Brookes & Demeler, 2008). Results are stored in the database and conveniently organized as web pages, which can be accessed by the data owners and authorized collaborators from anywhere on the Internet. New academic and not-for-profit users of UltraScan can request a new USLIMS instance on behalf of their institution at https://uslims.aucsolutions.com/lims_servers.php, after indicating their geographical region.
DATA ANALYSIS
The following steps discuss the recommended approach for obtaining optimal data analysis results. All methods described imply the use of the open-source UltraScan software, which is available for free download from https://www.ultrascan3.aucsolutions.com/software.php and in source code format from https://github.com/ehb54/ultrascan3. UltraScan's fitting methods are parallelized to provide unsurpassed computational performance and resolution, and are integrated into the USLIMS database backend. A multi-platform GUI interface for Windows, Macintosh, and Linux computers is available, and a high-performance computing (HPC) module is provided for use on large-scale shared parallel computing platforms such as those provided through the National Science Foundation's ACCESS framework. Not-for-profit users can obtain a free cloud-based USLIMS instance, which integrates the desktop GUI platform with remote cloud based storage and the HPC module. Additional configurations are available; for more information and additional help, please contact the author.
SV Experiments
After velocity data are collected in the Proteomelab instruments, each intensity dataset is converted to absorbance data by UltraScan and imported into the USLIMS database, where data from each triple (rotor hole, channel, and wavelength) are associated with the data owner, instrument, centerpiece, rotor and rotor stretch calibration, window type, and solution (containing details of analyte(s) and buffer). For the Optima AUC, use of the UltraScan data-acquisition module is recommended; this interfaces directly with the instrument to automatically retrieve the data from the instrument's database into the USLIMS database in its native binary double-precision floating-point format. Associations of solutions, rotor, centerpiece, etc. with the experiment are programmed into the data-acquisition module before the run is performed, when these details are readily available. Data in UltraScan are stored in the binary OpenAUC format (Cölfen et al., 2010) and can later be exported in legacy format compatible with data generated by the Proteomelab XLA/XLI/XLF instruments. After USLIMS import, the data are edited to visually define an initial meniscus position, to define a start and end point for the radial range to be analyzed, to remove spikes resulting from missed lamp flashes, and to exclude any unsuitable scans, such as baseline scans at the end of the experiment that do not contain any sedimentation information, or early scans that have overly steep boundaries that could amplify refractive artifacts.
After editing, data analysis begins by identifying the appropriate fitting range for the two-dimensional optimization problem of finding sedimentation and diffusion coefficients, as well as partial concentrations for all species that are potentially present in a mixture. The philosophy of data fitting embodied in UltraScan enforces a user-agnostic approach, in which the computer algorithm is supposed to find the correct solution without user-imposed bias for a particular model. Hence, a model-independent fitting approach is used for solving the general problem where sedimentation and diffusion coefficients can independently vary for each species, without unnecessary, and often unreasonable, constraints imposed by the algorithm or the user. Unlike other software packages, UltraScan solves the two-dimensional problem by creating a grid with dimensions m and n representing the resolution of the parameters s and D. To aid the user in identifying the proper diffusion range, the diffusion domain is typically parameterized by the frictional ratio, k = f/f 0, which allows the user to define the diffusion domain in terms of the degree to which a particle is non-globular, or anisotropic. Rearranging Eqn. 5 and solving for the diffusion coefficient, we obtain Eqn. 10:
Noninteracting solutes in experimental data, C D, can then be represented by a linear combination of simulated Lamm equation solutions, C S, across a two-dimensional set of grid points with dimensions m and n , where each grid point i ,j contributes a unique value of s and D , and each term's amplitude describes the partial concentration, ci,j , of each species, plus any baseline contribution, b :
For reversibly self-associating molecules, this model is modified to account for constraints between the partial concentrations of oligomeric species ci,j , as governed by the equilibrium constant(s) and kinetic rate constant(s) for these associations (Demeler et al., 2010; Kroe & Laue, 2009).
Optimization of these models is achieved by the least-squares method, which minimizes the sum of the squares of the differences between the experimental (C D) and simulated (C S) data at each radial and time point to obtain a minimal root mean square deviation (RMSD):
The RMSD is primarily a function of the appropriateness of the model, and inspection of the residuals should reflect only deviations due to stochastic noise, not systematic noise contributions (see Supporting Information Fig. S5E for an example of random deviations). In UltraScan, multiple optimization methods are employed to fit sedimentation data to a model. The choice of optimization method depends on the application. All experiments require a sequence of refinement steps that include the determination of time-invariant and radially invariant noise components, as well as optimization of the boundary conditions (meniscus and bottom of cell position), which are required for the solutions of the Lamm equation. The logic behind the choice of optimization method and sequence of refinement steps for different types of experimental systems is explained in detail below.
Optimization
Optimization is the process of refining the parameter values of an initial and imperfect estimated model to satisfy Eqn. 12. The closer the initial model is to the final model, the better are the chances the optimization process will find the global minimum for Eqn. 12. An initial model requires knowledge of the parameter ranges that need to be fitted. Because the parameter ranges are not known before the fit, and should not be subject to preconceived user bias, an overestimation of the initial data range is recommended. A model-independent approach to determine the s -value range is available through the d c /d t approach (Stafford, 1992), which is implemented in UltraScan to identify the s -value range for any data set, regardless of optical system used. This method effectively removes the time-invariant noise contributions present in all AUC data and provides reasonable, model-independent s -value estimates for an initial model. Due to the lack of diffusion deconvolution, d c /d t distributions tend to overestimate the actual s -range, but this is desirable, both because of the lack of precision of the d c /d t method and also because an underestimation of the s -value range will result in errors leading to poor fits. Subsequent optimization methods will automatically discard unnecessary s -values from consideration. An example of a d c /d t distribution is shown in Supporting Information Figure S1. The d c /d t estimate is used to set the s -value range for the two-dimensional spectrum analysis (2DSA; Brookes et al., 2010), the next step in the analysis. The frictional ratio range is harder to predict, so again, an overestimation is desirable. For proteins, the frictional ratio range should be set to 1-4, and can be extended if the sample is known to contain molecules with very extended shapes, such as fibrillar aggregates or long, linear DNA/RNA molecules.
2DSA is an optimization approach that uses a grid over sedimentation and frictional ratios to parameterize the range of possible solutes to be identified in the solution. Linear combinations of finite element solutions of the Lamm equation (Eqn. 1) are fitted by a non-negatively constrained least-squares approach (Lawson & Hanson, 1974) to obtain the concentrations of solutes present in the mixture. The initial 2DSA is performed on a parallel computer architecture with 8–16 cores, typically using a 64 × 64 grid setting. For s -value ranges exceeding multiple orders of magnitude, a custom grid can be designed with the custom grid model editor in UltraScan (Demeler et al., 2014) to place additional grid points into regions with more signal, using a less dense spacing in regions with little signal. The custom grid method is also needed when studying mixtures of sedimenting and floating particles. This situation occurs when studying proteins or other denser molecules that are loaded into lipid nanoparticles (LNP): Empty LNPs can have partial specific volumes larger than that of water, and therefore float, whereas loaded LNPs typically sediment (Henrickson et al., 2021). The custom grid method permits the use of different partial specific volume settings for regions in the grid with positive and negative buoyancy terms B (see Eqn. 13). When B is negative, molecules will float; when B is positive, they will sediment. When B is zero, the molecule will neither float nor sediment, and will simply contribute to the baseline absorbance, which should be captured in the time-invariant noise signal. For that reason, in UltraScan all s -values between −0.1 s and +0.1 s are excluded from the grid, regardless of speed, because they would not be resolvable in any experiment.
Once a grid has been chosen, the 2DSA analysis is used in a three-step process to refine the finite element model used to fit the experimental data. In the first 2DSA application, time-invariant noise correction is activated, but radially invariant noise correction must be turned off. The initial fit should be reviewed in the Finite Element Model Viewer in UltraScan to assess whether any aggregates are missed or nonrandom residuals are obtained. If this is the case, the fit should be repeated with modified parameters to address nonrandom residual patterns. The results can also be reviewed for evidence of clipping in the parameter space, which can be assessed with the pseudo-3D plots of the model. If random residuals are obtained, the same settings for the 2DSA method can be used throughout the 2DSA model refinement workflow.
The baseline offset shown in Eqn. 11 is composed of multiple contributions: time-invariant, radially invariant, buffer absorbance (which is non-sedimenting), and stochastic noise. The least-squares optimization algorithms require all terms in Eqn. 11 to be linearly independent; however, time-invariant and radially invariant noise contributions are linearly independent only if there is no buffer absorbance. When intensity data are collected, buffer absorbance is part of the total signal and can be modeled by both time- and radially invariant noise. Therefore, the buffer contribution violates the orthogonality requirement of the time-invariant and radially invariant noise simulation vectors in Eqn. 11, when both are fitted simultaneously. However, by using a stepwise refinement, this problem can be mitigated by modeling the buffer signal together with the time-invariant noise contribution in the initial fit, and then subtracting it from later fits. Once this signal is subtracted, time- and radially invariant noise are orthogonal and can be fitted simultaneously.
In the second refinement step, time- and radially invariant noise contributions are both fitted. In addition, the meniscus position is fitted. If the mixture contains small proteins, peptides, or degraded protein fragments, back-diffusion from the bottom of the cell will be significant, even at the highest speed possible, and the boundary shape will be affected by the emerging equilibrium gradient. In such cases, the bottom position should also be fitted.
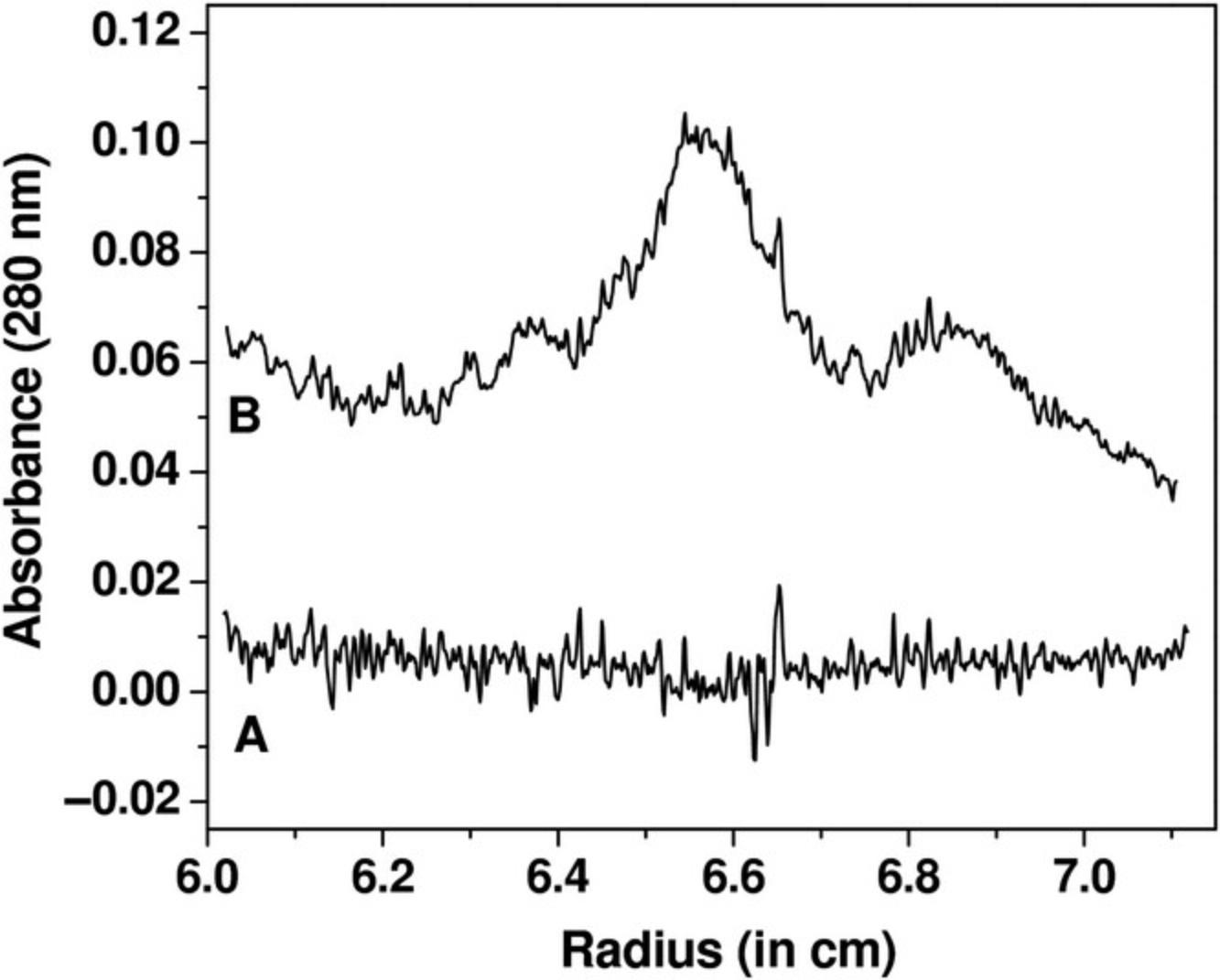
By default, both meniscus and bottom position are fitted by determining the RMSD values of 11 boundary positions, five on each side of the visually determined meniscus peak or the calculated bottom position (estimated from the rotor stretch calibration and the known centerpiece geometry (Stoutjesdyk et al., 2020)). The 11 test points extend 0.015 cm from the original boundary position recorded in the edit profile on each side, with the center point at the visually determined or calculated position. The resulting RMSD values are then plotted against the radius and fitted by a second-order polynomial to find the minimal RMSD position, which is then adopted as a best-fit meniscus or bottom position (see Supporting Information Fig. S2 for an example of a meniscus or bottom fit and Fig. S3 for an example for a simultaneous fit of both boundary conditions, fitting 11 × 11 = 121 boundary condition combinations). In the fit of the boundary conditions, both time- and radially invariant noise correction should always be turned on. A significant improvement in the RMSD will be seen in the boundary condition fit compared to the initial fit using only time-invariant noise.
In the final refinement, the new boundary conditions are used to refit the time- and radially invariant noise contributions using an iterative 2DSA approach, which will refine the original 2DSA solution by joining the nonzero grid elements with each subgrid, and refitting each subgrid until there is no more change in the solution (typically 3-10 iterations). The complete refinement workflow is illustrated in Supporting Information Figures S4 and S5. At this point, an optimal model has been determined, and additional algorithms can be employed to evaluate the data without the contributions of systematic noise.
If the 2DSA solution suggests the presence of only a few, discrete solutes, a parsimonious regularization by genetic algorithm (GA) analysis (Brookes & Demeler, 2007) of the 2DSA distribution is well advised. This method will remove false-positive solutes (caused by noise present in the data) from the distribution and refine the 2DSA solution by highlighting only essential components present in the solution. This approach can further be refined by also performing a 50- to 100-iteration Monte Carlo analysis (Demeler & Brookes, 2008) in conjunction with the GA analysis. If multiple speeds and concentrations were measured, a van Holde–Weischet analysis should be performed on each sample (Demeler & van Holde, 2004), and the s -value distributions should be overlaid for comparison. If the distributions suggest little change for the multiple conditions, further accuracy can be obtained by combining multiple speeds and multiple concentrations into a global 2DSA or GA fit. If concentration-dependent changes are apparent, the distributions should be evaluated to determine whether reversible oligomerizations appear to be present. In such a case, a nonlinear model can be used to fit the data to models describing user-defined reversibly reacting systems (Cao & Demeler, 2008; Demeler et al., 2010) with the discrete model genetic algorithm optimization method. For pure systems containing only oligomeric species, a molecular-weight-constrained 2DSA or GA analysis can be performed, constraining the solution to an approximate non-interacting model where only selected oligomeric forms presumed to be present in the solution are described. Subsequent refinement steps can improve resolution by reducing the range limits or increasing the number of grid points.
For systems displaying broad sedimentation coefficient distributions, a 2DSA-Monte Carlo fit with 100 iterations can improve the detection of trends in the distribution by attenuating the contributions of artifactual species caused by stochastic noise in the data. A useful check to confirm trends can be performed with the parametrically constrained spectrum analysis (PCSA; Gorbet et al., 2014). This method attempts to detect trends in oligomerization behavior when oligomerizing molecules change globularity as a function of molar mass. Because frictional ratio changes are sometimes poorly defined because of low diffusion signal, the constraints implemented in this method excel in reducing multi-valued, degenerate 2DSA fits to single lines in the sedimentation/frictional ratio domain.
A data analysis flowchart for SV experiments and additional tutorials for sedimentation experiments can be found at: https://resources.aucsolutions.com/tutorials.php
Multi-Wavelength AUC Analysis
SV experiments on molecular mixtures with different absorbance properties require additional analysis steps beyond the iterative two-dimensional spectrum analysis step discussed in the Optimization section. If multiple wavelengths have been measured for the same sample, each wavelength contributes a complete SV data set, which can be separately analyzed and then combined into a three-dimensional multi-wavelength sedimentation coefficient profile in UltraScan (see Fig. 6A). If the basis spectra of all spectral contributors are available, additional analysis steps can be applied to deconvolute these contributors into separate hydrodynamic datasets (see Fig. 6B). This analysis requires that each scan from each dataset originating from a different wavelength is measured at the same time. This is only possible with the multi-wavelength absorbance detector developed by H. Cölfen (Pearson et al., 2018; Strauss et al., 2008). Alternatively, in UltraScan, an iterative two-dimensional spectrum analysis model from each wavelength can be used to simulate each corresponding scan from each dataset for the same time point. The resulting projections over all wavelengths can be deconvoluted using a spectral decomposition tool in UltraScan. Separated SV datasets for each spectral species can then be analyzed by any method in UltraScan to provide sedimentation coefficient distributions, for example as shown in Figure 6B, by a model-independent approach that generates diffusion-corrected sedimentation coefficient distributions using the enhanced van Holde–Weischet method (Demeler & van Holde, 2004). The deconvolution of MW-AUC datasets requires extinction coefficient profiles covering all wavelengths included in the SV experiment. If these profiles are converted to molar extinction units, the resulting SV profiles for each species will be represented in molar units rather than in optical density units, and will allow direct stoichiometric evaluation of all species identified in the hydrodynamic analysis, which is very helpful to identify the composition and binding ratios of hetero-complexes. A detailed discussion of MW-AUC experiments, along with a step-by-step experimental design and data analysis details, can be found in Henrickson et al. (2022).
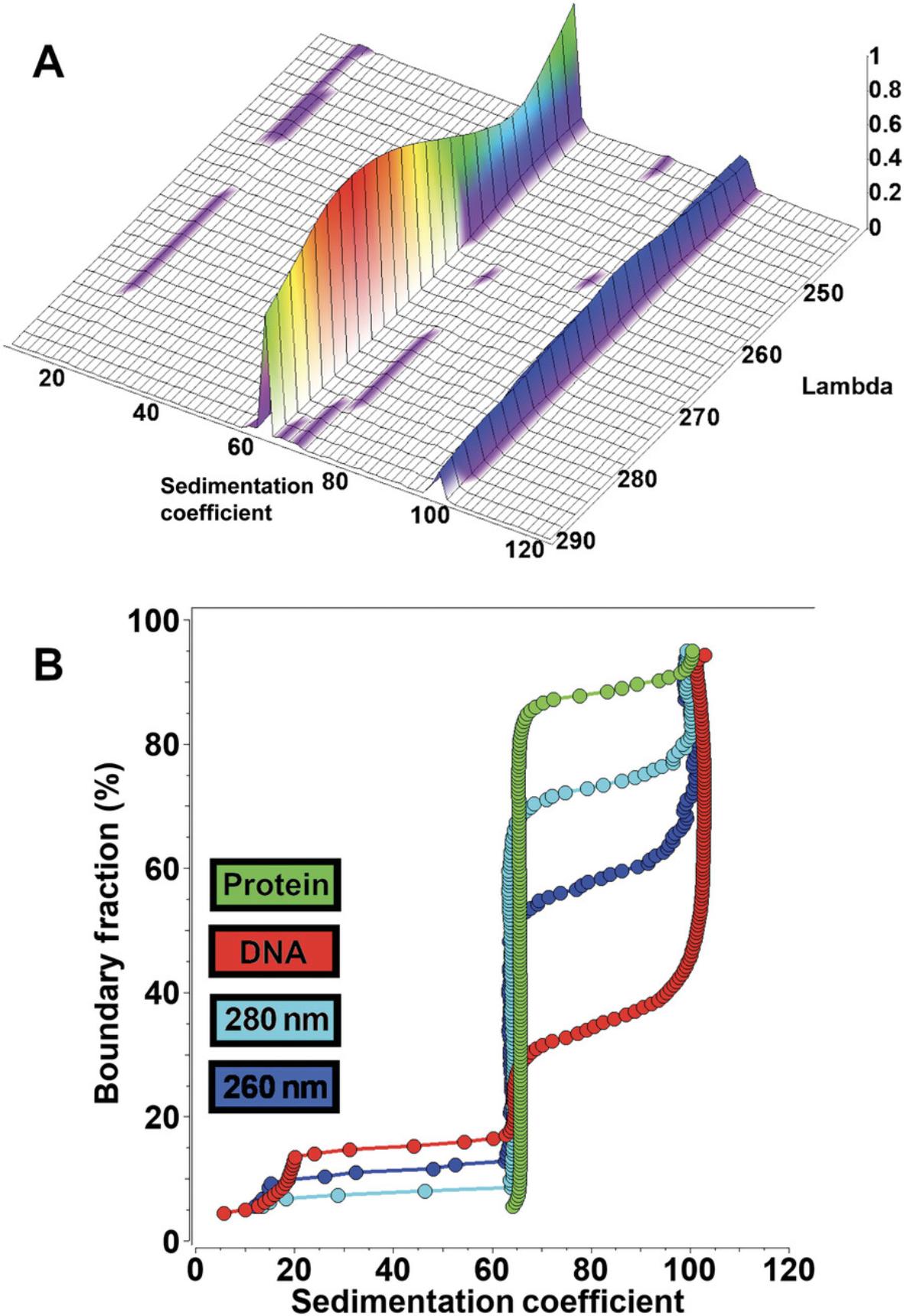
Experimental Diagnostics and Uncertainties
Finite element modeling of SV experiments returns sedimentation and diffusion coefficients, as well as partial concentrations, for individual solutes in a mixture. The accuracy of such modeling is subject to a number of factors. In addition to instrument-related uncertainties resulting from sources such as misaligned optical components, chromatic aberration, and inaccuracies from temperature and rotor speed detection or radial calibration, low lamp intensity, and noise in the data, factors related to the experimental system can also contribute to inaccuracies in the obtained results or difficulties in modeling the obtained data. Those include concentration-dependent nonideality, concentration-dependent self-association (mass action), pressure effects, and solvent gradient formation, as well as degradation and aggregation occurring during the experiment. All of these effects change the observed sedimentation coefficients of the analytes over time. But in many cases, it may not be necessary to obtain accurate sedimentation and diffusion coefficients; instead, a simple comparison of the changes in sedimentation profiles observed in response to a change in the experimental system can provide valuable insights that do not depend on absolute accuracy. Such changes may be caused by modifications in the buffer properties (pH, ionic strength, addition of small molecules, etc.), by changes in analyte concentration, or by differences between a wild-type and mutant protein. A very sensitive and intuitive approach to monitor such changes or diagnose various experimental properties is the enhanced van Holde–Weischet analysis (Demeler & van Holde, 2004; Demeler et al., 1997). This method provides a model-independent approach to generate diffusion-corrected integral sedimentation coefficient distributions, which can be readily compared to diagnose trends in the experimental system. These factors are illustrated and discussed below.
Concentration-dependent nonideality. Analytes may behave in a hydrodynamically nonideal fashion if the concentration is high enough to impede sedimentation and diffusion transport, causing molecules to slow down due to inter-molecular interactions, most often through charge repulsion or steric effects, much as transport is impeded when automobiles have to slow down on a busy highway. Because the concentration changes along the boundary developed in an SV experiment from near zero concentration at the baseline to the loading concentration in the plateau region, the concentration-dependent nonideality effect also varies along this gradient. In such cases, the sedimentation and diffusion coefficients will vary for each point in the gradient, even though only one unique analyte may be present. The first obvious diagnostic is the appearance of nonrandom residuals because routine methods that do not take into account such concentration-dependent nonideality effects can no longer explain the transport in the AUC cell. A simulated comparison between a nonideal system and an ideal model fit is shown in Figure 7, showing the effects of fitting a nonideal system with an ideal Lamm equation solution (in panels Fig. 7A-C), and a clear diagnosis can be obtained when multiple concentrations of the nonideal analyte are measured and their G(s) distributions are compared (Fig. 7D).
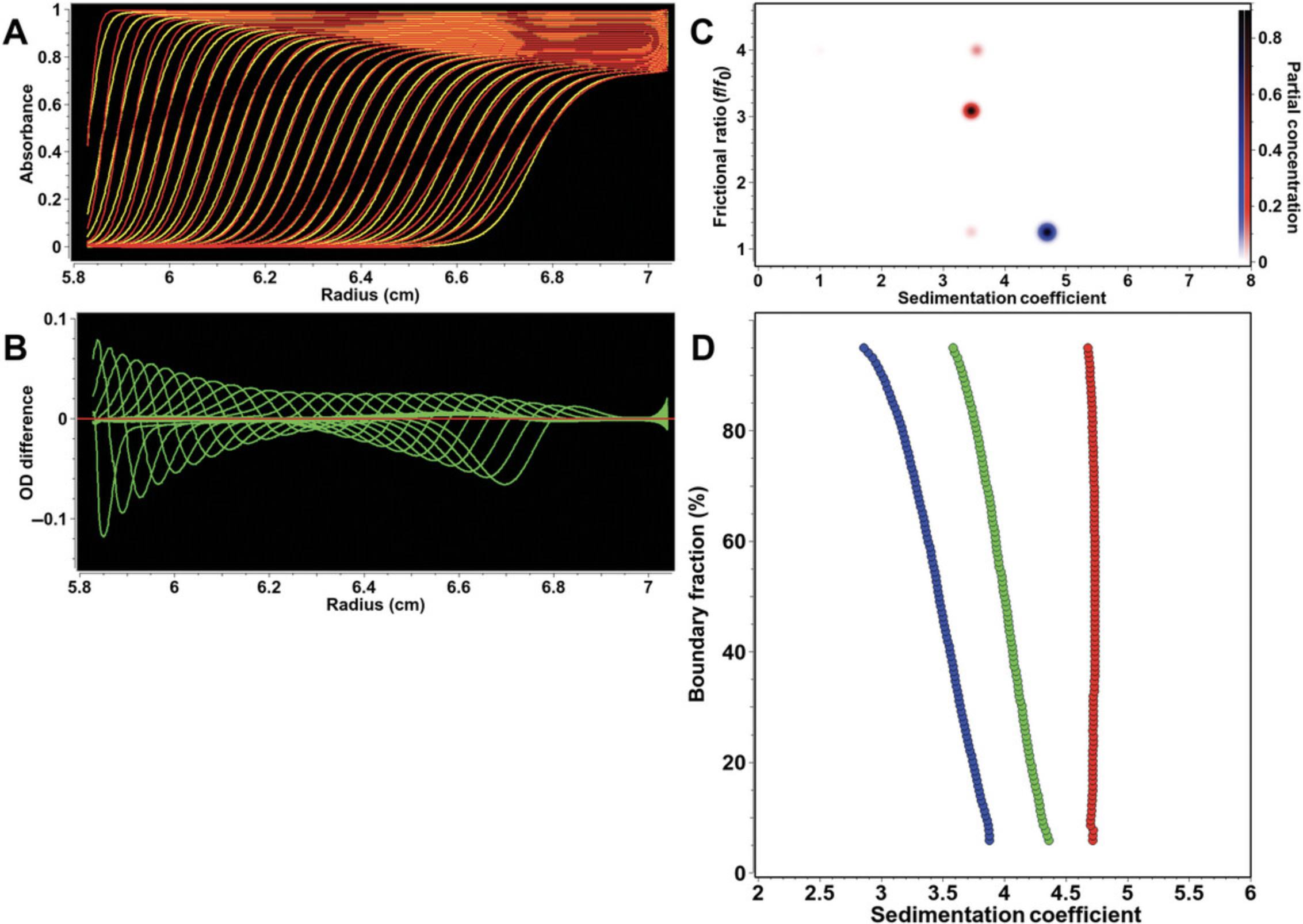
Reversible self-association. Another concentration-dependent effect relates to the mass action properties of a self-associating protein. As the concentration of the protein increases along the sedimenting boundary, the mass action effects cause the protein to oligomerize. Such oligomerization reactions are typically fast enough to equilibrate on the time scale of the velocity experiment, causing different ratios of monomeric and oligomeric forms to sediment at different boundary fractions. This situation can be approximated with a linear combination of noninteracting Lamm equation solutions that model the weight-average sedimentation coefficient and the gradient average diffusion coefficient of all oligomeric species present at a particular concentration. The shape of G(s) van Holde–Weischet distributions from such systems allows a clear identification of a reversible protein oligomerization system by comparing multiple concentrations. An enhanced van Holde–Weischet analysis of a self-associating monomer-dimer protein system with fast kinetics is shown in Figure 8, showing the characteristic half-parabola shape of the G(s) distribution. A more detailed analysis can be performed with the discrete model genetic algorithm analysis (Demeler et al., 2010), which also allows the fitting of equilibrium constants and slow reaction kinetics.
Time-dependent changes. Systems that are not at chemical equilibrium when studied by AUC can change their sedimentation and diffusion coefficients on a slower time scale than most reversible association reactions. Examples include aggregation or degradation occurring on the time scale of hours while the experiment is being performed. Such systems will generate nonrandom residuals during fitting, because the composition of the system changes between early and late scans of the experiment. Modeling approaches attempt to find the best compromise, but will fail to match early and late scans well. To diagnose this condition, UltraScan allows the creation of different edit profiles that select early, middle, and late scans into separate fits. Such systems typically see negligible changes over a shorter time period and can then be well fitted with low RMSD values and randomly distributed residuals when individual groups of early, middle, and late scans are analyzed separately. The time-dependent effect can then be plotted by overlaying the G(s) distributions of different time points in the experiment, clearly identifying the trend of compositional change. A more subtle, time-dependent effect is the evolution of an underlying density and viscosity gradient due to the presence of sedimenting buffer components, which then cause non-constant sedimentation and diffusion coefficients because the local concentration of the gradient forming material also affects the local density and viscosity, which in turn influence the apparent sedimentation and diffusion of any analytes differently at different times and locations in the AUC cell. Such gradients affect sedimentation and diffusion over time most dramatically at the top and the bottom of the cell. To diagnose such a condition, it is advisable to simulate the gradient-forming materials using the ASTFEM finite element simulation routine in UltraScan and to identify the radial regions and time points in the cell that exhibit the smallest concentration change in the gradient-forming material. A second edit profile should then apply the radial range and scan time range identified to be most constant, and the data should be refitted with this profile. If the RMSD values and residuals improve markedly, the result can still be informative, and mitigate the effects of density and viscosity change during the experiment.
Pressure effects. SV experiments performed at higher speeds can generate significant pressure gradients of several hundred bar across the radial range due to hydrostatic pressure effects of the solvent. Although most proteins are inert in this pressure regime, sometimes weak interactions between molecules may be affected, resulting in different compositions of the system at different radial positions. To identify the presence of such an effect, it is advisable to create two or three edit profiles with different radial ranges, separating data from all scans into top, middle, and bottom of the solution column. In such cases, refitting different column slices can generate acceptable fits, and the results from different pressure regimes in the cell can be compared by overlaying the sedimentation coefficient profiles from each slice.
Meniscus fitting. Determination of proper boundary conditions is essential for obtaining random residuals and low RMSD values. However, if the applied model does not properly describe the experimental data, the determination of boundary conditions through fitting is often compromised. This situation is easily detected by inspecting the meniscus fit (see Supporting Information Fig. S2). Meniscus positions resulting from the fit should be located well within the initial search region, and the obtained meniscus position should be compared with the visually determined meniscus position, and should show minimal difference. If the U-shaped fitting profile for the meniscus is absent, or shows a minimum outside of the indicated range, the experimental data should be evaluated for the presence of any of the factors listed above. If in doubt, the radial calibration should be repeated.
CHECKLISTS
Experimental Design and Data Collection Protocol
- 1.Before starting the AUC experiment, perform recommended diagnostic procedures and confirm that the instrument is in optimal operating condition (see Instrument Diagnostics).
- 2.The most appropriate speed for SV experiments can be determined by first simulating the experiment with the UltraScan ASTFEM simulation module using prior knowledge about the sample (molecular weight and partial specific volume from sequence, assembly state, k D, etc.). The speed should be chosen such that a minimum of 100 scans spanning the entire cell can be collected from each channel before pelleting. Account for differences in data acquisition speeds from different instruments; scan times in the Optima AUC are typically four times faster measurements in the Proteomelab XLA. A slower rotor speed in the initial experiment may reveal the presence of aggregates. If in doubt, compare the fitted total concentration from the iterative 2DSA model with the concentration measured in a benchtop spectrophotometer to make sure that no material has been lost to observation, accounting for variations in cuvette and AUC cell pathlengths. If aggregates are not detected, a higher speed can be used later to emphasize resolution and more clearly identify sample heterogeneity.
- 3.ABDE experiments are the method of choice for determining the density of a mixture of solutes. For such experiments, (a) the choice of density gradient material needs to cover the expected density range and (b) the analytes must be compatible with either ionic or non-ionic gradient material. To minimize refractive effects, a 3-mm-pathlength centerpiece is recommended. The rotor speed and loading concentration of the gradient material determines the dynamic range of the density, and a long column experiment maximizes the resolvable density. Simulating the density gradient material at different speeds reveals the density minimum and maximum in the density gradient. A lower speed with a well-matched loading concentration of the gradient material will resolve analytes that are closely spaced in density. Larger molecules have smaller diffusion coefficients and will generate narrower peaks than smaller molecules.
- 4.To detect the presence of reversible self-association or concentration dependent nonideality, multiple concentrations should be measured. At least two concentrations differing at least three-fold should be measured, centered around the concentration of interest. In the Optima AUC, MW-AUC can be employed to extend the concentration range to 10-fold or more. 450-460 µl of sample in a transparent buffer system with a moderate amount of salt (20-50 mM) should be used as a first test (see Absorbance optics section). In the Proteomelab XLA, a 0.3-OD sample should be placed into the reference channel and a 0.9-OD sample in the sample channel of the same cell. In the Optima AUC, a 0.5- to 0.7-OD sample will provide the best signal-to-noise ratio. Interference or fluorescence detection can be used to further extend the concentration range. See the Experimental Design section for additional details regarding sample preparation.
- 5.For samples containing absorbing buffer components, interference optics can be used instead, or the wavelength can be adjusted to optimize sample extinction while minimizing buffer absorption. See the Background section above for a discussion of the selection of optical systems. Carefully align all cells in the rotor. Up to four cells, containing up to eight samples, can be measured simultaneously at speeds of up to 60 krpm in the An60Ti rotor when using the UltraScan data acquisition program with the UV-visible detector. When using interference optics, up to three samples (in three cells), with a counterbalance in hole 4, can be used in the An60Ti rotor. Likewise, eight cells (up to 16 samples) can be measured at speeds of up to 50 krpm in the An50Ti rotor in UV-visible intensity mode, or seven samples in seven cells with a counterbalance in hole 8 when using Rayleigh interference optics. Fluorescence optics also require a counterbalance in hole 4 or 8, but allow two samples per cell to be measured.
- 6.Wait for the temperature of the rotor to stabilize at zero RPM, under vacuum (the instrument will switch to a different temperature detector that measures the rotor temperature directly when the vacuum drops below 50 μm), before accelerating the rotor to the selected speed. As soon as the selected speed has been reached, start to collect scans until the sample is either at equilibrium or pelleted. Collect data without time delay between scans, as fast as the machine can collect. Excessive or unnecessary scans can be deleted during data editing. Compare the meniscus positions of the first three or four scans for each channel to confirm that the cells are not leaking. If a leak is detected, the rotor should be decelerated immediately to prevent damage to the centerpiece.
- 7.If the equilibrium constant is of interest, the concentration should be chosen such that both monomer and oligomeric species are sufficiently abundant to obtain enough signal from all species. Multiple experiments at different wavelengths or optical systems may be required to find the optimal concentration range.
- 8.Proceed with USLIMS data import, pseudo-absorbance data conversion, and editing of the data.
Sedimentation Velocity Analysis and Result Interpretation
Proceed with the 2DSA analysis as outlined above. After satisfactory fits are obtained from an iterative 2DSA model, an enhanced van Holde–Weischet analysis should be performed and the G(s) distributions should be compared for a first-order evaluation of the results. In this analysis, a vertical G(s) distribution indicates the presence of a pure, homogeneous distribution (see the red line in Fig. 7 and the green and blue lines in Fig. 8 for examples). A positive slope indicates heterogeneity in the sample, which can be caused by either molar mass heterogeneity or frictional heterogeneity, or both. A positive slope with the shape of a right-half second-order polynomial often indicates reversible monomer-dimer equilibria. In such a case, always check for concentration-dependent self-association. A negative slope indicates concentration-dependent nonideality (see Fig. 7D and associated discussion). The following outcomes are common, and can be discerned easily from a velocity experiment.
1.The sample is homogeneous. Initialize a GA analysis (Brookes & Demeler, 2007) with the model obtained in the iterative 2DSA analysis; this will provide detailed sedimentation and diffusion coefficients. When followed by a GA–Monte Carlo analysis (Demeler & Brookes, 2008), initialized with the GA model, confidence limits for the determined parameters can be obtained. A Monte Carlo analysis will also enhance the signal-to-noise ratio and determine the confidence intervals of the solute parameters. This approach is valid for non-interacting systems, and it will result in molecular weights, partial concentrations, and relative shape information for each detected solute. 2.The sample is pauci-disperse, with no more than four or five discrete species. A change in concentration has no apparent effect on the sedimentation coefficient distributions. Proceed as in (a); see Brookes & Demeler (2007) for a detailed discussion of the analysis of such systems. 3.The sample displays clear concentration-dependent, reversible association properties (see Fig. 8 and related discussion above). Continue with a discrete model GA analysis (Demeler et al., 2010) to obtain k D equilibrium constants and k off rates. Review the models from Monte Carlo analyses to obtain valuable clues about the molar masses of the oligomeric species present in the system. It should be noted that the 2DSA models non-interacting systems. If the system is reversibly self- or hetero-associating, these methods will only approximate the true composition by reporting weighted average values for the species present. Fits of the reversible reaction boundary generate averages of all oligomers present at each point in the boundary. This average is a function of the concentration at that point, and reflects the weighted average sedimentation coefficient and the gradient average diffusion coefficient. However, the information from these analyses together with the results from the van Holde–Weischet analysis generally provide unambiguous clues to the type of association that needs to be modeled, and the results can then be used to formulate a possible reaction model and initialize the parameters for a reacting model. Parameter optimization for nonlinear reaction models is best accomplished with the genetic algorithm analysis performed in conjunction with a Monte Carlo analysis. The parameter distributions obtained in this fashion provide important clues about the most likely parameter ranges, especially for frictional ratios, equilibrium constants, and kinetic rate constants of the reaction, which are otherwise difficult to obtain. If several models are plausible, each should be checked for compatibility with the experimental data. The best model should be chosen based on the parsimony of parameters, randomness of the residuals, and the overall residual mean square deviation (RMSD). If the monomer molecular weight is known from sequence or mass spectrometry, the molar mass can be held constant in the model and the partial specific volume can be floated instead, and considered constant across all oligomeric species. 4.The sample is very heterogeneous and displays a broad sedimentation distribution. Continue with a PCSA (Gorbet et al., 2014) or 2DSA-Monte Carlo analysis (Brookes et al., 2010; Demeler & Brookes, 2008) to better define trends in the distribution. 5.The sample is mostly homogeneous, but also contains a small amount of irreversible aggregate or a low-molecular-weight contaminant or degradation product. Changing the loading concentration does not affect the sedimentation coefficient distribution or relative composition. The sample contains multiple components that do not interact or affect the composition. Proceed as in (a). 6.For cases in which the analysis results in broad, very heterogeneous sedimentation coefficient distributions (8d), the resolution of individual components may be compromised by the heterogeneity. In such a case, the genetic algorithm optimization is not very useful because a parsimonious regularization is not indicated. Instead, further purification and fractionation of the sample may be desirable.
For most systems, additional precision can be obtained by performing a global fit over multi-speed experiments and/or use of replicate samples in order to best identify the partial contributions of low-concentration contaminants or aggregates (Demeler & Gorbet, 2016; Ranasinghe et al., 2023). Whereas high-speed experiments emphasize the signal for sedimentation coefficients and composition, a low-speed experiment will allow all samples to diffuse long enough before pelleting to provide additional signal on the diffusion coefficient. Because molecular weight determinations rely on knowledge of both the sedimentation and the diffusion coefficient (see Eqn. 4), the combined fit of a low-speed and a high-speed experiment also provides enhanced information about molecular weight and shape of the solute(s). Such global analyses should also be performed in conjunction with Monte Carlo analysis to maximize the statistical certainty of the observations.
CONCLUSION
Analytical ultracentrifugation is a powerful technique for measuring recombinant proteins and other macromolecules in solution. Sedimentation velocity experiments can be used to assess purity and composition to compare many hydrodynamic, thermodynamic, and molecular parameters between mutants and wild type and allow the experimentalist to follow changes in equilibrium constants, rate constants, conformation, and composition. A careful experimental design and judicious application of the appropriate optical system and data analysis procedure is critical for a successful experiment, as are the necessary diagnostics to assure reliable instrument operation. The general and model-independent fitting methods implemented in UltraScan provide a maximum in resolution and flexibility, while at the same time taking much of the guesswork out of AUC data interpretation.
Acknowledgments
This work was performed at the Canadian Center for Hydrodynamics at the University of Lethbridge and supported by grants to the author, including from the Canada 150 Research Chairs program (C150-2017-00015), the US National Institutes of Health (GM-120600), and the Canadian Natural Science and Engineering Research Council (DG-RGPIN-2019-05637). The Canadian Center for Hydrodynamics is funded by the Canada Foundation for Innovation (CFI-37589). UltraScan supercomputer calculations were supported through NSF/ACCESS (MCB070039N) and the University of Texas (TG457201).
Author Contributions
Borries Demeler : Conceptualization; data curation; formal analysis; funding acquisition; investigation; methodology; project administration; resources; software; supervision; validation; visualization; writing—original draft; writing—review and editing.
Conflict of Interest
The author declares no conflict of interest.
Open Research
Data Availability Statement
Data available on request from the author.
Supporting Information
| Filename | Description |
|---|---|
| cpz1974-sup-0001-figuresS1.png157.5 KB | Figure S1 Example of a time-derivative analysis of an edited velocity data set in UltraScan. A time slice of data, excluding data early in the experiment and excluding data without a stable plateau at the end of the experiment, provides a good initial guess for the sedimentation coefficient fitting range, in this case approximately from 2 to 15 S. The time-derivative method eliminates time-invariant noise, which is clearly visible in this example, from the experimental data and provides a model-independent estimate of the sedimentation coefficient range. Because diffusion contributes to the sedimentation coefficient range, s-value ranges obtained in this way will overestimate the actual range, which is desirable, because clipping this range will degrade the quality of the fit. |
| cpz1974-sup-0001-figuresS2.png38.1 KB | Figure S2 Fit for a one-dimensional boundary condition determination from a sedimentation velocity experiment (meniscus or cell bottom position, fitted separately). RMSD values for individual, fixed radial positions are fitted in the general vicinity of the estimated boundary condition to a second-order polynomial. The center point (point no. 6; green line) was the initial guess; the cyan line marks the best fit radial position. Note that the fitted minimum position is not necessarily coincident with a previously fitted position. |
| cpz1974-sup-0001-figuresS3.png370 KB | Figure S3 Fit for a two-dimensional boundary condition determination from a sedimentation velocity experiment (meniscus and cell bottom position fitted simultaneously). RMSD values for individual, fixed radial positions are fitted in the general vicinity of the estimated boundary condition to a second-order polynomial. The center point (point no. 6; green line) was the initial guess; the cyan line marks the best fit radial position. |
| cpz1974-sup-0001-figuresS4.png2 MB | Figure S4 Two-dimensional spectrum analysis (2DSA) refinement of intensity data from a sedimentation velocity experiment. (A) Raw experimental data containing radially invariant, time-invariant, and stochastic noise, as well as baseline offsets from buffer absorbance. (B) Refinement after removing initial time-invariant noise profile, including the buffer contribution, as can be seen from the apparent 0.2 OD baseline offset. Also, the residuals bitmap on the right side of the plot shows horizontal lines, suggesting the presence of radially invariant noise that has not been removed yet. RMSD: 4.54 × 10−3. (C) Meniscus fit with time- and radially invariant noise fit. Only minor systematic patterns remain. RMSD: 3.31 × 10−3. (D) Final refinement using the iterative 2DSA, removing all systematic noise contributions, leaving only stochastic noise. RMSD: 3.27 × 10−3. |
| cpz1974-sup-0001-figuresS5.png166.9 KB | Figure S5 Three types of noise contributions to AUC data. (E) Stochastic noise, cannot be fitted and contributes to the RMSD observed after the 2DSA fit is refined with the iterative approach. (F) Time-invariant noise. This noise originates primarily from the variations in the photomultiplier tube response, and any imperfections in cell windows or optical components. The 2DSA algorithm also includes any buffer absorbance, or absorbance from non-sedimenting components in the mixture, in the fitted time-invariant noise component. In this case, it is clear that ∼0.2 OD result from buffer absorbance. (G) Radially invariant noise. This noise component arises from variations in the baseline over time, and is typically caused by lamp intensity fluctuations and variations in the pathlength of the interference optics due to heating and cooling cycles. Radially invariant noise has typically a much smaller amplitude than time-invariant noise. |
Please note: The publisher is not responsible for the content or functionality of any supporting information supplied by the authors. Any queries (other than missing content) should be directed to the corresponding author for the article.
LITERATURE CITED
- Ahmed, I., Hahn, J., Henrickson, A., Khaja, F. T., Demeler, B., Dubnau, D., & Neiditch, M. B. (2022). Structure–function studies reveal ComEA contains an oligomerization domain essential for transformation in gram-positive bacteria. Nature Communications , 13(1), 7724. https://doi.org/10.1038/s41467-022-35129-0
- Brookes, E., Cao, W., & Demeler, B. (2010). A two-dimensional spectrum analysis for sedimentation velocity experiments of mixtures with heterogeneity in molecular weight and shape. European Biophysics Journal , 39(3), 405–414. https://doi.org/10.1007/s00249-009-0413-5
- Brookes, E., & Demeler, B. (2007). Parsimonious regularization using genetic algorithms applied to the analysis of analytical ultracentrifugation experiments. GECCO '07: Proceedings of the 9th Annual Conference on Genetic and Evolutionary Computation , London, 361–368. https://doi.org/10.1145/1276958.1277035, ACM 978-1-59593-697-4/07/0007
- Brookes, E., & Demeler, B. (2008). Parallel computational techniques for the analysis of sedimentation velocity experiments in UltraScan. Progress in Colloid & Polymer Science, 286, 138–148.
- Cao, W., & Demeler, B. (2005). Modeling analytical ultracentrifugation experiments with an adaptive space-time finite element solution of the Lamm equation. Biophysical Journal , 89, 1589–1602. https://doi.org/10.1529/biophysj.105.061135
- Cao, W., & Demeler, B. (2008). Modeling analytical ultracentrifugation experiments with an adaptive space-time finite element solution for multi-component reacting systems. Biophysical Journal , 95, 54–65. https://doi.org/10.1529/biophysj.107.123950
- Cölfen, H., Laue, T. M., Wohlleben, W., Schilling, K., Karabudak, E., Langhorst, B. W., Brookes, E., Dubbs, B., Zollars, D., Rocco, M., & Demeler, B. (2010). The Open AUC Project. European Biophysics Journal , 39(3), 347–359. https://doi.org/10.1007/s00249-009-0438-9
- Cölfen, H., Wohlleben, W., & Walter, J. (n.d.) A multi-wavelength detector for the Beckman Optima XL. OpenAUC documents and license terms, accessed January 28, 2024. https://wiki.aucsolutions.com/openAUC/
- Demeler, B. (n.d.). The UltraScan-III software repository on Github, accessed January 28, 2024. https://github.com/ehb54/ultrascan3
- Demeler, B. (2010). Methods for the design and analysis of sedimentation velocity and sedimentation equilibrium experiments with proteins. Current Protocols in Protein Science , 60, 7.13.1–7.13.24. https://doi.org/10.1002/0471140864.ps0713s60
- Demeler, B., & Brookes, E. H. (2008). Monte Carlo analysis of sedimentation experiments. Colloid and Polymer Science , 286(2), 129–137. https://doi.org/10.1007/s00396-007-1699-4
- Demeler, B., Brookes, E., Wang, R., Schirf, V., & Kim, C. A. (2010). Characterization of reversible associations by sedimentation velocity with UltraScan. Macromolecular Bioscience , 10(7), 775–782. https://doi.org/10.1002/mabi.200900481
- Demeler, B., & Gorbet, G. (2016). Analytical ultracentrifugation data analysis with UltraScan-III. In S. Uchiyama, W. F. Stafford, & T. Laue (Eds.), Analytical ultracentrifugation: Instrumentation, software, and applications (pp. 119–143). Springer.
- Demeler, B., Nguyen, T. L., Gorbet, G. E., Schirf, V., Brookes, E. H., Mulvaney, P., El-Ballouli, A. O., Pan, J., Bakr, O. M., Demeler, A. K., Hernandez Uribe, B. I., Bhattarai, N., & Whetten, R. L. (2014). Characterization of size, anisotropy, and density heterogeneity of nanoparticles by sedimentation velocity. Analytical Chemistry , 86(15), 7688–7695. https://doi.org/10.1021/ac501722r
- Demeler, B., Saber, H., & Hansen, J. C. (1997). Identification and interpretation of complexity in sedimentation velocity boundaries. Biophysical Journal , 72(1), 397–407. https://doi.org/10.1016/S0006-3495(97)78680-6
- Demeler, B., & van Holde, K. E. (2004). Sedimentation velocity analysis of highly heterogeneous systems. Analytical Biochemistry , 335(2), 279–288. https://doi.org/10.1016/j.ab.2004.08.039
- Gabir, H., Gupta, M., Meier, M., Heide, F., Koch, M., Stetefeld, J., & Demeler, B. (2023). Investigation of dynamic solution interactions between NET-1 and UNC-5B by multi-wavelength analytical ultracentrifugation. European Biophysics Journal , 52(4–5), 473–481. https://doi.org/10.1007/s00249-023-01644-1
- Giebeler, R. (1992). The Optima XL-A: A new analytical ultracentrifuge with a novel precision absorption optical system. In S. E. Harding, A. J. Rowe, & J. C. Horton (Eds.), Analytical ultracentrifugation in biochemistry and polymer science (pp. 16–25). Royal Society of Chemistry.
- Gorbet, G., Devlin, T., Hernandez Uribe, B. I., Demeler, A. K., Lindsey, Z. L., Ganji, S., Breton, S., Weise-Cross, L., Lafer, E. M., Brookes, E. H., & Demeler, B. (2014). A parametrically constrained optimization method for fitting sedimentation velocity experiments. Biophysical Journal , 106(8), 1741–1750. https://doi.org/10.1016/j.bpj.2014.02.022
- Gorbet, G. E., Mohapatra, S., & Demeler, B. (2018). Multi-speed sedimentation velocity implementation in UltraScan-III. European Biophysics Journal , 47(7), 825–835. https://doi.org/10.1007/s00249-018-1297-z
- Gorbet, G. E., Pearson, J. Z., Demeler, A. K., Cölfen, H., & Demeler, B. (2015). Next-generation AUC: Analysis of multiwavelength analytical ultracentrifugation data Methods in Enzymology , 562(1), 27–47. https://doi.org/10.1016/bs.mie.2015.04.013
- Henrickson, A., Ding, X., Seal, A. G., Qu, Z., Tomlinson, L., Forsey, J., Gradinaru, V., Oka, K., & Demeler, B. (2023). Characterization and quantification of adeno-associated virus capsid-loading states by multi-wavelength analytical ultracentrifugation with UltraScan. Nanomedicine , 18(22), 1519–1534. https://doi.org/10.2217/nnm-2023-0156
- Henrickson, A., Gorbet, G. E., Savelyev, A., Kim, M., Hargreaves, J., Schultz, S. K., Kothe, U., & Demeler, B. (2022). Multi-wavelength analytical ultracentrifugation of biopolymer mixtures and interactions. Analytical Biochemistry , 21, 114728. https://doi.org/10.1016/j.ab.2022.114728
- Henrickson, A., Kulkarni, J. A., Zaifman, J., Gorbet, G. E., Cullis, P. R., & Demeler, B. (2021). Density matching multi-wavelength analytical ultracentrifugation to measure drug loading of lipid nanoparticle formulations. ACS Nano , 15(3), 5068–5076. https://doi.org/10.1021/acsnano.0c10069
- Horne, C. R., Henrickson, A., Demeler, B., & Dobson, R. C. J. (2020). Multi-wavelength analytical ultracentrifugation as a tool to characterise protein-DNA interactions in solution. European Biophysics Journal , 49(8), 819–827. https://doi.org/10.1007/s00249-020-01481-6
- Horne, C. R., Venugopal, H., Panjikar, S., Wood, D. M., Henrickson, A., Brookes, E., North, R. A., Murphy, J. M., Friemann, R., Griffin, M. D. W., Ramm, G., Demeler, B., & Dobson, R. C. J. (2021). Mechanism of NanR gene repression and allosteric induction of bacterial sialic acid metabolism. Nature Communications , 12(1), 1988. https://doi.org/10.1038/s41467-021-22253-6
- Iranzo, O., & Kumar, D. (2009). Absorbance spectra for common buffer systems. https://resources.aucsolutions.com/images/reductants.png
- Johnson, C. N., Gorbet, G. E., Ramsower, H., Urquidi, J., Brancaleon, L., & Demeler, B. (2018). Multi-wavelength analytical ultracentrifugation of human serum albumin complexed with porphyrin. European Biophysics Journal , 115(2), 328–340. https://doi.org/10.1007/s00249-018-1301-7
- Kar, S. R., Kingsbury, J. S., Lewis, M. S., Laue, T. M., & Schuck, P. (2000). Analysis of transport experiments using pseudo-absorbance data. Analytical Biochemistry , 285(1), 135–142. https://doi.org/10.1006/abio.2000.4748
- Kim, H., Brookes, E., Cao, W., & Demeler, B. (2018). Two-dimensional grid optimization for sedimentation velocity analysis in the analytical ultracentrifuge. European Biophysics Journal , 47(7), 837–844. https://doi.org/10.1007/s00249-018-1309-z
- Kingsbury, J. S., Klimtchuk, E. S., Laue, T. M., Théberge, R., Costello, C. E., & Connors, L. H. (2008). The modulation of transthyretin tetramer stability by cysteine-10 adducts and the drug diflunisal: Direct analysis by fluorescence-detected analytical ultracentrifugation. Journal of Biological Chemistry , 283, 11887–11896. https://doi.org/10.1074/jbc.M709638200
- Kroe, R. R., & Laue, T. M. (2009). NUTS and BOLTS: Applications of fluorescence-detected sedimentation. Analytical Biochemistry , 390(1), 1–13. https://doi.org/10.1016/j.ab.2008.11.033
- Lamm, O. (1929). Die Differentialgleichung der Ultrazentrifugierung. Arkiv för Matematik , Astronomi och Fysik , 21B, 1–4.
- Laue, T. M. (1996). Choosing which optical system of the Optima XL-I analytical ultracentrifuge to use. Beckman Publication. http://www.beckmancoulter.com/literature/Bioresearch/1821a(a).pdf
- Lawson, C. L., & Hanson, R. J. (1974). Solving least squares problems. Prentice-Hall, Inc.
- MacGregor, I. K., Anderson, A. L., & Laue, T. M. (2004). Fluorescence detection for the XLI ultracentrifuge. Biophysical Chemistry , 108, 165–185. https://doi.org/10.1016/j.bpc.2003.10.018
- Mortezazadeh, S., & Demeler, B. (2023). Systematic noise removal from analytical ultracentrifugation data with UltraScan. European Biophysics Journal , 52(4-5), 203–213. https://doi.org/10.1007/s00249-023-01631-6
- Pearson, J., Hofstetter, M., Dekorsy, T., Totzeck, M., & Cölfen, H. (2018). Design concepts in absorbance optical systems for analytical ultracentrifugation. Analyst , 143(17), 4040–4050. https://doi.org/10.1039/C8AN00706C
- Pearson, J. Z., Krause, F., Haffke, D., Demeler, B., Schilling, K., & Cölfen, H. (2015). Next-generation AUC adds a spectral dimension: Development of multiwavelength detectors for the analytical ultracentrifuge. Methods in Enzymology , 562(1), 1–26.
- Pearson, J., Walter, J., Peukert, W., & Cölfen, H. (2018). Advanced multiwavelength detection in analytical ultracentrifugation. Analytical Chemistry , 90(2), 1280–1291. https://doi.org/10.1021/acs.analchem.7b04056
- Ranasinghe, M., Fogg, J. M., Catanese, D. J. Jr., Zechiedrich, L., & Demeler, B. (2023). Suitability of double-stranded DNA as a molecular standard for the validation of analytical ultracentrifugation instruments. European Biophysics Journal , 52(4-5), 267–280. https://doi.org/10.1007/s00249-023-01671-y
- Richter, K., Wurm, C., Strasser, K., Bauer, J., Bakou, M., VerHeul, R., Sternisha, S., Hawe, A., Salomon, M., Menzen, T., & Bhattacharya, A. (2023). Purity and DNA content of AAV capsids assessed by analytical ultracentrifugation and orthogonal biophysical techniques. European Journal of Pharmaceutics and Biopharmaceutics , 189, 68–83. https://doi.org/10.1016/j.ejpb.2023.05.011
- Savelyev, A., Brookes, E. H., Henrickson, A., & Demeler, B. (2023). A new UltraScan module for the characterization and quantification of analytical buoyant density equilibrium experiments to determine AAV capsid loading. European Biophysics Journal , 52(4–5), 311–320. https://doi.org/10.1007/s00249-023-01641-4
- Schuck, P., & Demeler, B. (1999). Direct sedimentation analysis of interference optical data in analytical ultracentrifugation. Biophysical Journal , 76, 2288–2296. https://doi.org/10.1016/S0006-3495(99)77384-4
- Stafford, W. (1992). Boundary analysis in sedimentation transport experiments: A procedure for obtaining sedimentation coefficient distributions using the time derivative of the concentration profile. Analytical Biochemistry , 203, 295–301. https://doi.org/10.1016/0003-2697(92)90316-Y
- Sternisha, S. M., Wilson, A. D., Bouda, E., Bhattacharya, A., & VerHeul, R. (2023). Optimizing high-throughput viral vector characterization with density gradient equilibrium analytical ultracentrifugation. European Biophysics Journal , 52(4–5), 387–392. https://doi.org/10.1007/s00249-023-01654-z
- Stoutjesdyk, M., Henrickson, A., Minors, G., & Demeler, B. (2020). A calibration disk for the correction of radial errors from chromatic aberration and rotor stretch in the Optima AUC™ analytical ultracentrifuge. European Biophysics Journal , 49(8), 701–709. https://doi.org/10.1007/s00249-020-01434-z
- Strauss, H. M., Karabudak, E., Bhattacharyya, S., Kretzschmar, A., Wohlleben, W., & Cölfen, H. (2008). Performance of a fast fiber based UV/Vis multiwavelength detector for the analytical ultracentrifuge. Colloid and Polymer Science , 286(2), 121–128. https://doi.org/10.1007/s00396-007-1815-5
- Williams, T. L., Gorbet, G. E., & Demeler, B. (2018). Multi-speed sedimentation velocity simulations with UltraScan-III. European Biophysics Journal , 47(7), 815–823. https://doi.org/10.1007/s00249-018-1308-0
- Zhang, J., Pearson, J. Z., Gorbet, G. E., Cölfen, H., Germann, M. W., Brinton, M. A., & Demeler, B. (2017). Spectral and hydrodynamic analysis of West Nile Virus RNA-protein interactions by multiwavelength sedimentation velocity in the analytical ultracentrifuge. Analytical Chemistry , 89(1), 862–870. https://doi.org/10.1021/acs.analchem.6b03926

