Computational Pipeline for Analysis of Biomedical Networks with BioNAR
Colin McLean, Colin McLean, Anatoly Sorokin, Anatoly Sorokin, J. Douglas Armstrong, J. Douglas Armstrong, Oksana Sorokina, Oksana Sorokina
Abstract
In a living cell, proteins interact to assemble both transient and constant molecular complexes, which transfer signals/information around internal pathways. Modern proteomic techniques can identify the constituent components of these complexes, but more detailed analysis demands a network approach linking the molecules together and analyzing the emergent architectural properties. The Bioconductor package BioNAR combines a selection of existing R protocols for network analysis with newly designed original methodological features to support step-by-step analysis of biological/biomedical . Critically, BioNAR supports a pipeline approach whereby many networks and iterative analyses can be performed. Here we present a network analysis pipeline that starts from initiating a network model from a list of components/proteins and their interactions through to identifying its functional components based solely on network topology. We demonstrate that BioNAR can help users achieve a number of network analysis goals that are difficult to achieve anywhere else. This includes how users can choose the optimal clustering algorithm from a range of options based on independent annotation enrichment, and predict a protein's influence within and across multiple subcomplexes in the network and estimate the co-occurrence or linkage between metadata at the network level (e.g., diseases and functions across the network, identifying the clusters whose components are likely to share common function and mechanisms). The package is freely available in Bioconductor release 3.17: https://bioconductor.org/packages/3.17/bioc/html/BioNAR.html. © 2023 The Authors. Current Protocols published by Wiley Periodicals LLC.
Basic Protocol 1 : Creating and annotating the network
Support Protocol 1 : Installing BioNAR from RStudio
Support Protocol 2 : Building the sample network from synaptome.db
Basic Protocol 2 : Network properties and centrality
Basic Protocol 3 : Network communities
Basic protocol 4 : Choosing the optimal clustering algorithm based on the enrichment with annotation terms
Basic Protocol 5 : Influencing network components and bridgeness
Basic Protocol 6 : Co-occurrence of the annotations
INTRODUCTION
The technology available to support biological experiments has made rapid advances in recent years, with massive steps forward in both the sensitivity and throughput of methods to analyze biological samples across multiple levels. The most widely known advances are those in the high-throughput sequencing of DNA and RNA, but there have been step changes in a wide range of areas, including proteomics, metabolomics, and connectomics. Integrating these datasets into network models allows us to elucidate key functional interactions, pathways, and complexes that are required for healthy function and that, when perturbed, often lead to disease.
Proteomic data are typically represented via static undirected protein-protein interaction (PPI) networks, in which vertices represent the proteins and edges represent the molecular interactions. From a PPI network, one can derive many statistical measures of topology and fundamental properties and use these to gain insight and make predictions about the underlying data (Bánky et al., 2013; Vidal et al., 2011). For example, “scale-free” (Barabasi & Albert, 1999) properties and small-world paths, found in many biological networks, in combination with various centrality measures, such as degree and betweenness, have been widely used to identify “hub” molecules, which often encode disease-related proteins (Vidal et al., 2011).
Protein networks obtained from modern proteomic studies are usually large (thousands of proteins) and contain the components of multiple signaling pathways, linked together by other proteins whose roles in the network are less well understood. A common approach is to divide PPI networks into communities (or clusters) based on their connecting architecture, which can be achieved with multiple clustering algorithms.
Proteins in a network model are usually annotated with functional or/and disease information. Given the topological structure from clustering, it is often useful to test how these annotations are distributed throughout the network: Do they tend to concentrate in specific network communities? Do some annotations share common subnetwork patterns? To study this, disease and/or functional associations can be mapped over PPI vertices. Functional and disease enrichment of clusters can then be calculated using a suitable hypothesis driven test, i.e., the hypergeometric test, and tested against a permutation study (McLean et al., 2016) to reveal the clusters within the network that are significantly enriched for specific annotations. This kind of approach has been extensively applied in our set of case studies and was used to link together neuronal diseases (typically highly polygenic) onto the molecular pathways and clusters in the synapse proteome (Pocklington et al., 2006). In summary, a common and important task in biological network analysis is in testing how well the network topology (interconnectedness) correlates with distribution of specific functional (or dysfunctional/disease) annotations (Fernandez et al., 2009; Klemmer et al., 2009; Zhu et al., 2007).
We designed BioNAR to provide a universal topologically based network analysis pipeline deployable on high-performance computing environments that enables users to load networks generated and/or annotated using their lab's own metadata and perform a step-by-step network analysis with respect to their specific scientific questions, while also making the tool as widely applicable and flexible as possible.
Six main protocols presented here form a procedural guide for network analysis using BioNAR (Fig. 1). Basic Protocol 1 describes how to initiate a network model, import relevant datasets, and annotate the network with various metadata. This results in a base network model, on which all the other analyses in the pipeline are then based. Support Protocol 1 explains how to install the BioNAR package using R integrated development environment (IDE) RStudio. Basic knowledge of R language is assumed.
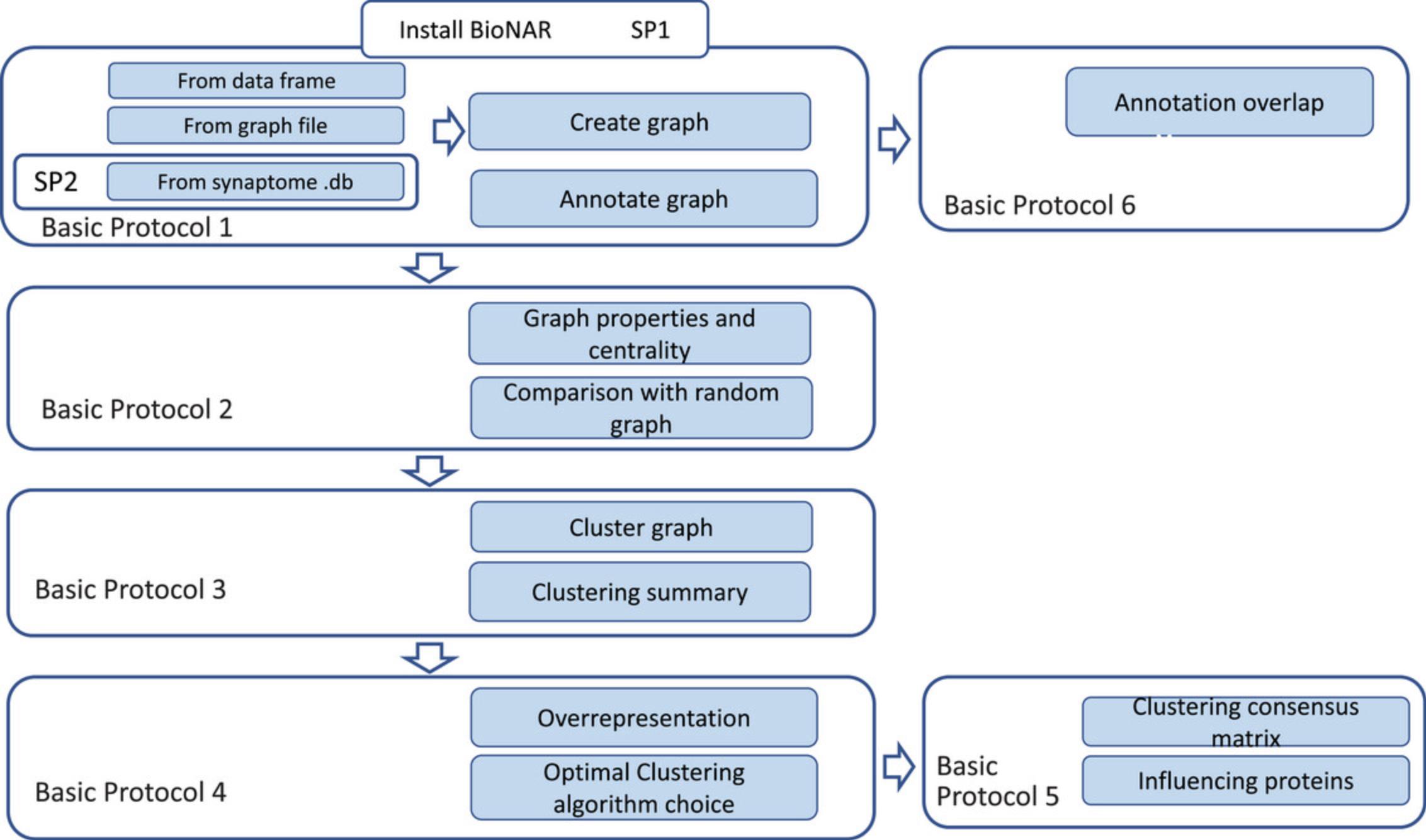
In Basic Protocol 2, the raw network model is analyzed as a whole and its general properties, e.g., “scale-freeness” and major network centralities, are calculated and compared against those of randomly generated network models of the same size. Basic Protocol 3 describes how to subdivide the network into communities using a selection of nine available algorithms that have been used in a range of published studies. Basic Protocol 4 further compares the results of different clustering algorithms and estimates their effectiveness based on a general assumption that biologically plausible clusters are more likely to show community enrichment with relevant functional annotation terms. Basic Protocol 5 then shows how to estimate the vertex property bridgeness based on the consensus clustering matrix, and how to rank the vertices based on their topological importance within the network. This can be used to identify candidate linkages between functional compartments in the model. Finally, Basic Protocol 6 demonstrates how to test the topological overlap of different annotations, which may indicate shared mechanisms that are only visible using the network context.
Given our previous and ongoing work is related to synaptic proteome, we illustrate the package's functionality with a postsynaptic network model, derived from the publicly available synaptome.db package (version 0.99.12), which is described in Support Protocol 2.
Basic Protocol 1: NETWORK INITIATION AND ANNOTATION
This protocol describes how a network is initiated in the BioNAR package and how annotations are added for further analysis. BioNAR implements networks as R data frames, in which each row corresponds to a vertex interactor pair and each vertex has a unique identifier (vertex_ID). Therefore, a network can be directly uploaded as a data frame in this format. Alternatively, a network can be imported from most standard graph file formats, including .gml and other formats supported by the igraph R package. BioNAR also allows network import for synaptic protein sets/synaptic compartments/brain regions directly from the synaptome.db package (Sorokina et al., 2022); this is described in Support Protocol 1.For constructing the protein interaction networks described here, we selected the NCBI Gene Entrez ID to use as a unique “vertex_ID” for each node/protein.
Many graph-related algorithms behave poorly when applied to graphs containing disconnected components. Consequently, most biological networks—including PPI networks—are constructed to retain only the network's largest connected component of vertices. We follow this practice for downstream analysis as well, but BioNAR also stores the disconnected components, as they may be of importance to the user at a later stage.
Vertices are typically annotated with categorical or continuous metadata. Annotations are usually handled in a three-column data frame format, where the first column contains the annotation term ID, the second column the annotation term name, and the third column the associated vertex_ID. All annotation terms for the same vertex_ID are collected and converted into semicolon-separated lists to store all annotations of the vertex held as a string in the vertex annotation. For example, if a protein is annotated with two different molecular functions A and B, in vertex annotation it will be stored as “A; B.”
In proteomic networks, annotations typically include Gene Ontology (GO) annotations and gene-disease association values (GDAs), and the direct import of both of these types of annotations from public databases is implemented in BioNAR. However, the package supports any custom annotation, including gene-expression values, pathway membership data, and so on. As an example of adding custom data, this protocol describes the addition of new binary annotation for the SynGo ontology (Koopmans et al., 2019). BioNAR is also designed to allow the user to assign the results of any vertex calculation as a new vertex attribute. The ability to retain such calculated supports reproducibility, as many algorithms used in network analysis have a stochastic component, so that multiple invocations of the same analysis can create a distribution of results, which can now all be stored for later analysis.
Necessary Resources
Hardware
- A modern compute environment capable of running R version >4.3.0 and RStudio version >2022.12.0
Software
- R version >4.3.0 and RStudio version >2022.12.0
Files
-
Sample network files (for the examples described) PSD_PPI.txt and/or PSDnetwork.gml (see Supporting Information), or your own data files in either format
-
Additional annotation file provided for illustrative purposes (see Supporting Information): SynGO.txt
1.Install RStudio and BioNAR package as described in Support Protocol 1.
Open RStudio and launch the library BioNAR, as well as a few more frequently used libraries, assuming they have not been installed by default. Navigate (using the command setwd) to the directory in which you have stored the network and annotation files (in our case, it is called “Sample network”).
- library(BioNAR)
- library(synaptome.db)
- library(ggplot2)library(pander)
- library(ggrepel)
- library(randomcoloR)
- setwd(“∼/Documents/Sample network”)
2.Load your network. This can be done in any of three ways; examples of each format are provided below, using the same test network below.
-
a. Import a network from a text table:
-
t <- read.table(“PSD_PPI.txt”, sep = “\t”, header = T, stringsAsFactors = F)
-
head(t)
-
gg <- buildNetwork(t)
-
summary(gg)
-
b. Import a network from a graph/.gml file:
-
g <- igraph::read.graph(“PSDnetwork.gml”,format=“gml”) #graph from gml
-
summary(g)
The commands summary(gg) and summary(g) will show the same graph composition from the text import (step 2a) or .gml import (step 2b), respectively: 2297 vertices and 9406 edges, with the Human Entrez ID used as the node name for all three graphs.
- c. Import network from synaptome.db (see Support Protocol 1).
3.Annotate the network with GeneNames. In this step, the raw graph from step 2 are annotated by importing annotation data from the human genome-wide gene annotation database org.Hs.eg.db. For each node in the graph, the Entrez Gene Name is assigned using the annotateGeneNames function.
- g<-annotateGeneNames(g)
- Sometimes gene IDs become obsolete and gene names are not assigned. We can check for this:
- any(is.na(V(g)$GeneName))
- If the result is TRUE, we can find such genes and assign its GeneName manually. Some functions further down require unique GeneNames to function correctly.
- idx<-which(is.na(V(g)$GeneName))
- idx
- V(g)$GeneName[idx]<-‘AKAP2’
4.Annotate the network with metadata. In this step, the raw graph from step 2 is annotated by importing annotation data from relevant external files and/or databases. For each node in the graph, the following annotation is added: associated human diseases are extracted directly from the Human Disease Ontology (HDO) using the annotateTopOntoOVG function and Gene Ontology terms (BP, MF, and CC) are extracted using the annotateGOont function.
- afile<-system.file(“extdata”, “flatfile_human_gene2HDO.csv”, package = “BioNAR”)
- dis <- read.table(afile,sep=“\t”,skip=1,header=FALSE,strip.white=TRUE,quote=“”)
- g <- annotateTopOntoOVG(g, dis)
- g <- annotateGOont(g)
- summary(g)
After calling summary(g), you will see that nodes now have attributes: id (v/n), name (v/c), GeneName (v/c), TopOnto_OVG (v/c), TopOnto_OVG_HDO_ID (v/c), GO_MF_ID (v/c), GO_MF (v/c), GO_BP_ID (v/c), GO_BP (v/c), GO_CC_ID (v/c), and GO_CC (v/c), where id corresponds to internal graph ID, name – Human Entrez ID, TopOnto_OVG is the disease name according to the Human Disease Ontology (HDO), TopOnto_OVG_HDO_ID is the disease ID according to the HDO, GO_MF_ID is the Gene Ontology Molecular Function ID, GO_MF is the Gene Ontology Molecular Function name, GO_BP_ID is the Gene Ontology Biological Process ID, GO_BP is the Gene Ontology Biological Process name, GO_CC_ID is the Gene Ontology Cell Compartment ID, and GO_CC is the Gene Ontology Cell Compartment name. (v/c) and (v/n) indicate that the corresponding attributes are character and numerical values associated with vertices.
To annotate a graph with your own metadata, you need to provide it in the form of a data frame (see example “SynGO.txt”), where the first column should contain vertex IDs matching name IDs in the network (Human Entrez ID) and the second column the respective attribute values. When using the command annotateVertex(g), you will need to provide the name of your new attribute as the parameter name (“syngo” in our case) and the name of your annotation table as the parameter values (“sg”).
- sg <- read.table(“SynGO.txt”, sep = “\t”, header = T, stringsAsFactors = F)
- g <- annotateVertex(g, name = “syngo”, values = sg, idatt = “name”)
If you call summary(g), you will now see an additional new attribute “syngo” in addition to those listed above.
Support Protocol 1: INSTALLING BioNAR FROM RStudio
Support Protocol 1 describes how install BioNAR from Bioconductor.
Necessary Resources
Hardware
- A modern compute environment capable of running R version >4.3.0 and RStudio version >2022.12.0.
Software
- R version >4.3.0 and RStudio version >2022.12.0
Files
- None
1.Download R from __https://www.r-project.org/, open the installer, and follow the installation prompts.
2.Download RStudio Desktop from https://www.rstudio.com, open the installer, and follow the installation prompts.
3.Open RStudio and install the Bioconductor package BioNAR using the following commands.
1.if (!require(“BiocManager”, quietly = TRUE)) 2.install.packages(“BiocManager”) 3.BiocManager::install(version = “3.17”) 4.BiocManager::install(“BioNAR”) 5.library(BioNAR) 6. This will check for and then install the Bioconductor package manager “BiocManager” if it is not already installed. It will then install BioNAR from Bioconductor. 7. During the installation process, BiocManager may determine that some packages are obsolete; in this case, it will ask: 8. Old packages: ‘x.y.z’, … 9. Update all/some/none? [a/s/n]: 10. If this is the first package you are installing, we suggest typing “n”; if you've already have a working R environment, it is wise to type “a”.
4.Install additional utility packages:
- BiocManager::install(c(“pander”, ‘randomcoloR’, ‘ plotly’ ))
5.Check that the library is installed correctly by using the command:
- library(BioNAR)
Support Protocol 2: BUILDING THE SAMPLE NETWORK FROM synaptome.db
BioNAR includes a direct plug-in to the Synaptic Proteome database, which contains 64 independent proteomic studies of mammalian synapses, recently curated into a single dataset describing a landscape of ∼8000 proteins (Sorokina et al., 2021). BioNAR does this through the Bioconductor package synaptome.db, which allows users to obtain the corresponding gene information, such as subcellular localization, molecular interactions, brain region, gene ontology, and disease association, and to construct customized protein-protein interaction network models for gene sets and entire subcellular compartments (Sorokina et al., 2022).
Support Protocol 2 describes how to extract a custom PPI network for postsynaptic compartment based on a gene set comprising proteins that were found in three or more independent postsynaptic studies.
Necessary Resources
Hardware
- A modern compute environment capable of running R version >4.3.0 and RStudio version >2022.12.0.
Software
- R version >4.3.0 and RStudio version >2022.12.0
Files
- none
1.Open RStudio and install the Bioconductor package synaptome.db using following commands.
-
if (!require(“BiocManager”, quietly = TRUE))
-
install.packages(“BiocManager”)
-
BiocManager::install(version = “3.17”)
-
BiocManager::install(“synaptome.db”)
-
library(synaptome.db)
This will check for and then install the Bioconductor package manager “BiocManager” if it is not already installed. It will then install synaptome.db from Bioconductor. During the installation process, BiocManager may determine that some packages are not the most recent version; in that case, it will ask:
- Old packages: ‘x.y.z’, …
- Update all/some/none? [a/s/n]:
If it is the first package you are installing, we suggest typing “n”; if you already have a working R environment, it seems wise to type “a”.
2.Extract the compartment ID for postsynaptic compartment. To do this, navigate using setwd to the directory where you will store all the results; in our case this is “Sample network”. The command match will return the database ID for required compartment, which is “1” in our case (for the postsynaptic compartment).
- setwd(“∼/Documents/Sample network/”)
- cid <-match(“ Postsynaptic ” , getCompartments()$Name)
- cid
3.Get all the gene IDs for the specified compartment.
- t<-getAllGenes4Compartment(cid)
- dim(t)
4.Select a subset of genes that were found in three or more studies.
In our example, the gene list for the postsynaptic compartment is large (5568 genes), and we want to reduce it to the highest-confidence set of genes, found in at least three (arbitrary decision) different studies, which results in 2643 genes. To get this, we specify “3” for the findGeneByCompartmentPaperCnt command.
- gp <- findGeneByCompartmentPaperCnt(3)
- postgp <- gp[gp$Localisation == “Postsynaptic”,]
- dim(postgp)
- head(postgp)
5.Build the PPI for the selected set of genes.
- library(BioNAR)
- ggb<-buildFromSynaptomeGeneTable(postgp, type = “limited”)
- write_graph(ggb, file = “PSDnetwork.gml”, format = “gml”)
Protein-protein interactions will be returned for a “limited” type of the network, which includes only genes presented in the list. The BioNAR command buildFromSynaptomeGeneTable creates a “limited”-type network and returns its largest connected component.
Basic Protocol 2: NETWORK PROPERTIES AND CENTRALITY
To assess any network model for biological plausibility, we often want to test a network's degree distribution for evidence of scale-free structure and compare it against an equivalent randomized network model. The assumption here is that a network based on noisy data will have more random architecture, whereas biological networks typically tend towards a more scale-free structure. For this we use the R PoweRlaw package (version 0.50.0; Gillespie, 2015), which deploys a goodness-of-fit approach to estimate the lower bound and the scaling parameter of the discrete power-law distribution for the optimal description of the graph degree distribution.
Although degree is the most commonly used vertex metric, there are other centrality metrics that can be estimated from the graph structure. BioNAR directly supports the calculation of the following network vertex centrality measures. Some are implemented via igraph (Gabor & Tamas, 2006): degree (DEG), betweenness (BET), clustering coefficient (CC), and page rank (PR; see igraph manual for details). Other measures appear only in BioNAR: semilocal centrality (SL), mean shortest path (mnSP), and standard deviation of the shortest path (sdSP).
Calculated vertex centrality values can be added as vertex attributes (calcCentrality) or returned as an R matrix (getCentralityMatrix), depending on user preference. Any other numerical characteristics, calculated for vertices and represented in a matrix form, can also be stored as a vertex attribute (applyMatrixToGraph).
To enable comparison of an observed network's vertex centrality values to those of an equivalently sized randomized graph, we enabled three randomization models: the G(n ,p) Erdös-Rényi model (Erdös & Rényi, 1959; “gnp,” illustrated in the example below), the Barabasi-Albert preferential attachment model (Barabási & Albert, 1999; “pa”), and the derivation of a new randomized graph from a given graph by iteratively and randomly adding/removing (“cgnp”) or rewiring edges (“rw”).
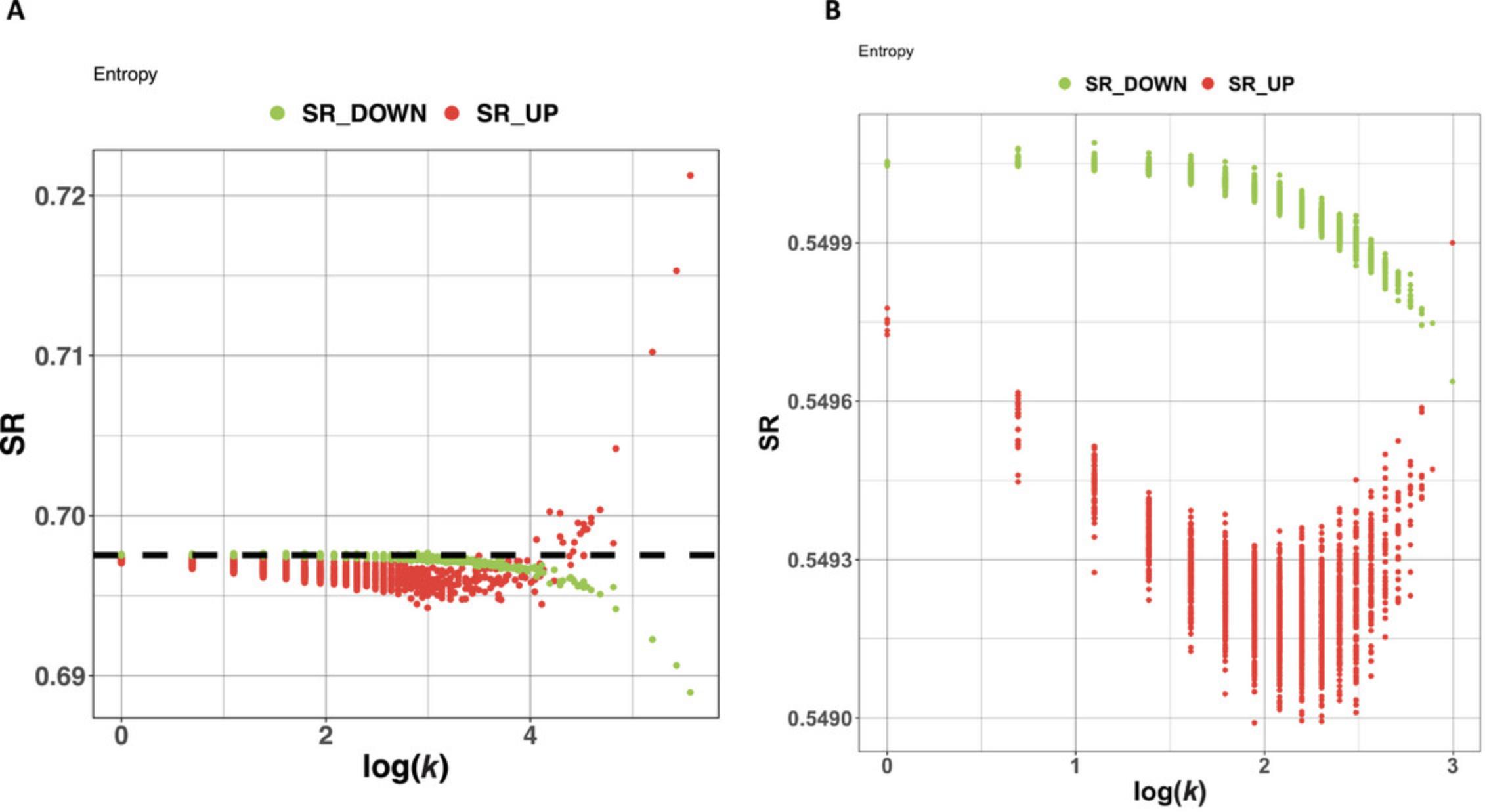
For proteomic networks with matching multi-condition gene-expression data, scale-free structure has also been demonstrated by using the expression data to perform a perturbation analysis on the network to measure network entropy (Teschendorff et al., 2015). Originally, this kind of analysis was designed for comparing a control with a perturbed network (e.g., wild-type versus mutant, untreated versus treated), where vertices with low entropy rate appear to be the most important players in disease propagation.
However, the assessment of scale-free structure does not actually require gene-expression data, as it based solely on the network topology. In BioNAR, following the procedure described by Teschendorff et al. (2015), all vertexes are artificially assigned a uniform weight and then sequentially perturbed, with the global entropy rate (SR) after each protein's perturbation being calculated and plotted against the log of the protein's degree (see Theoretical Appendix for more detail). In case of scale-free or approximate scale-free topologies, we see a clear bimodal response between over-weighted vertices and their degree and an opposing biphasic response in under-weighted vertices and their degrees.
Basic Protocol 2 starts with estimating and fitting the observed graph degree distribution to a power law and comparing this against a random network. At the next step, we estimate the graph entropy, again comparing it to the random graph. Finally, we estimate the range of centrality metrics for our graph and a randomly generated graph; in our example, we use the Erdös-Rényi model.
1.Check the network degree distribution.
- pFit <- fitDegree(as.vector(igraph::degree(graph=g)), Nsim=1000,
- plot=TRUE,WIDTH=2480, HEIGHT=2480)
- pwr <- slot(pFit,‘alpha’)
This command will take the graph created in Basic Protocol 1, fit it to a power-law distribution, and return a figure consisting of a log-log plot of the cumulative distribution function (CDF) of postsynaptic PPI network degree distribution (Fig. 2A). During fitting, code performs a bootstrapping hypothesis test to determine whether a power-law distribution is plausible. The number of bootstrapping rounds is defined by the parameter Nsim , which is set to 100 by default. Setting the Nsim parameter to large values makes calculation slower: for example, with Nsim = 1000 it takes couple of minutes to get a fit. By using a slot function, we extract scaling coefficient α to compare with the random graph results.
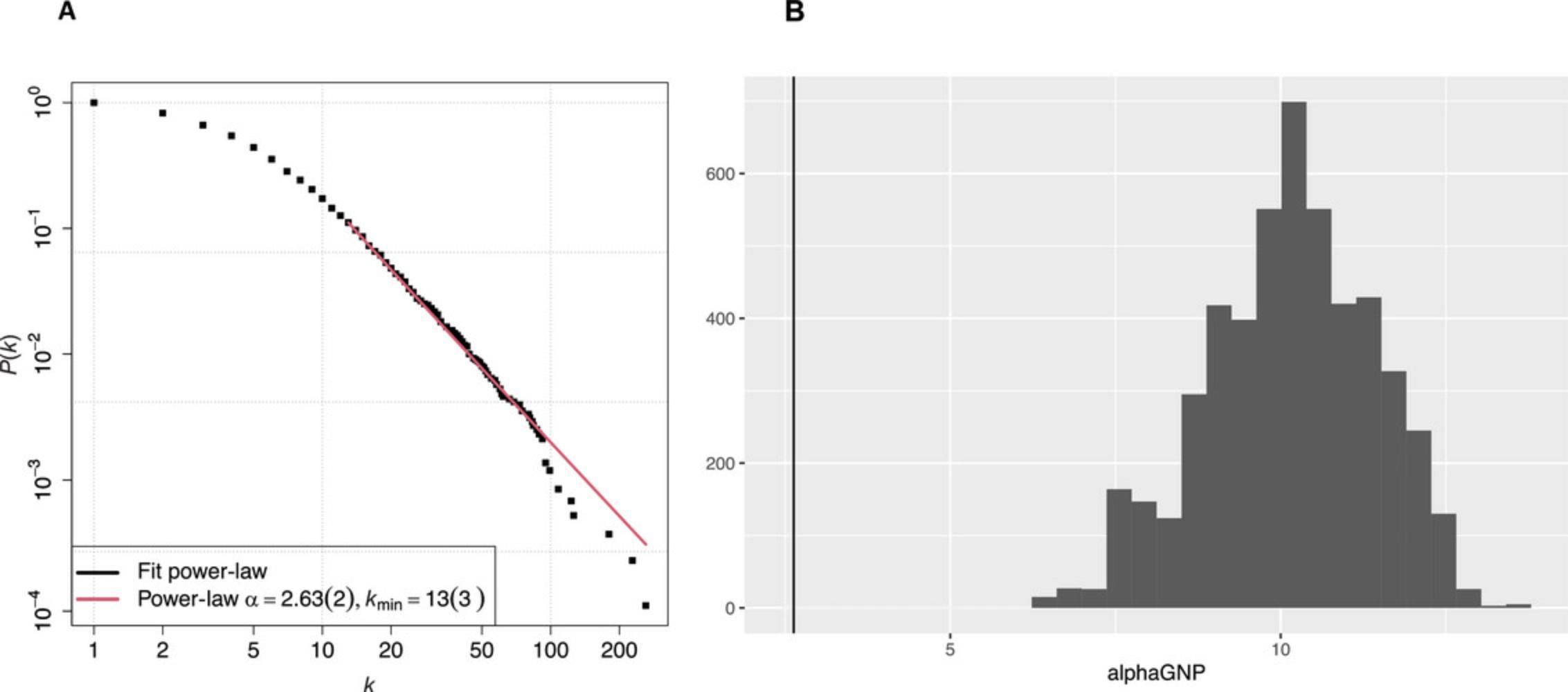
2.Compare network degree distribution with a set of random graphs.
The following commands will generate a sample of 5000 random G(n ,p) Erdös-Rényi graphs and estimate α coefficients of their best fits to the power-law distribution. To save compute time, we reduce the number of bootstrapping tests to 10 in this example; however, it still takes about hour and a half to complete the task, using 500 samples instead of 5000 to save time. The histogram of obtained values is plotted in Figure 2B, where the vertical line on the left indicates the value (2.63) for the actual graph.
-
lrgnp<-list()
-
alphaGNP<-c()
-
for(i in 1:5000){
- rgnp<-BioNAR:::getGNP(g)
- pFit <- fitDegree( as.vector(igraph::degree(graph=rgnp)),
- Nsim=10, plot=FALSE,threads=5
- p <- slot(pFit,“alpha”)
- lrgnp[[i]]<-rgnp
- alphaGNP[i]<-p
-
}
-
qplot(alphaGNP)+geom_vline(xintercept = pwr)
3.Calculate graph entropy.
As we do not have actual expression data for our graph, we can use simulated data (see the Theoretical Appendix for more detail). The command getEntropyRate estimates the global entropy rate for the whole network, whereas getEntropy estimates entropy value for each network vertex. The command plotEntropy visualizes the results as a plot (Fig. 3A).
- ent <- getEntropyRate(g)
- ent
- SRprime <- getEntropy(g, maxSr = ent$maxSr)
- head(SRprime)
- plotEntropy(SRprime, subTIT = “Entropy”, SRo = ent
maxSr)
4.Calculate the graph centrality measures.
- g <- calcCentrality(g)
The command calcCentrality assigns centrality measures the following node attributes: DEG, degree; BET, betweenness; CC, clustering coefficient; SL, semilocal centrality; mnSP, mean shortest path; PR, page rank; and sdSP, standard deviation of the shortest path. Rather than saving these centrality values on the graph, e.g., to provide different names for the vertex centrality attributes, they are obtained in matrix form:
- mc <- getCentralityMatrix(g)
The matrix will contain eight columns for each of the measures above, with the rows corresponding to each node's database ID (2297 nodes in total, synaptome.db version 0.99.12).
5.Calculate the graph centrality measures for a randomized graph.
- ggrm <- getRandomGraphCentrality(g, type = c(“cgnp”))
We need to select the type of randomization, “cgnp” in our case, that corresponds to a sampling algorithm, which will randomly perturb the graph adjacency matrix and shuffle its vertices in such a way that the correlation between new and old adjacency matrix is 75%.
Basic Protocol 3: IDENTIFYING THE NETWORK COMMUNITY STRUCTURE WITH CLUSTERING
This protocol splits the network into communities using a non-exhaustive set of commonly used clustering algorithms for molecular networks. These include modularity-maximization-based algorithms, such as the popular agglomerative “fast-greedy community” algorithm (fc; Clauset et al., 2004), the process-driven agglomerative random walk algorithm “Walktrap” (wt; Pons & Latapy, 2006), the coupled Potts/simulated annealing algorithm “SpinGlass” (sg; Reichardt & Bornholdt, 2006; Traag & Bruggeman, 2009), the divisive spectral-based “leading-eigenvector” (lec; Newman, 2006) and fine-tuning (Spectral; McLean et al., 2016) algorithms, and the hierarchical agglomerative “Louvain” algorithm (louvain; Blondel et al., 2008). We also included a non-modularity information-theory-based algorithm, “InfoMAP” (infomap; Rosvall & Bergstrom, 2008; Rosvall et al., 2009). All algorithm implementations, apart from Spectral, are imported from R's igraph package (Gabor & Tamas, 2006). The Spectral algorithm (McLean et al., 2016) was written in C++ and wrapped in R within a satellite CRAN package, rSpectral (https://cran.r-project.org/web/packages/rSpectral/index.html), linked to BioNAR. Default parameters used in the fc, lec, sg, wt, and louvain algorithms were chosen to maximize the measure modularity (Newman & Girvan, 2004); infomap seeks the optimal community structure in the data by maximizing the objective function called the minimum description length (Rissanen, 1978; Grünwald et al., 2005).
In this protocol, first, community structures are obtained for the network used in previous protocol. The user can select some or all of the available clustering algorithms to run simultaneously. This community structure(s) can then be visualized. The process can also be iterated by re-clustering the largest communities after each cycle (the threshold for communities to be re-clustered can be defined). Finally, we extract a summary table that compares across all the clustering algorithms used in the analysis.
1.Use the network g obtained with previous protocols.
2.Cluster the network.
We provide two functions, calcClustering and calcAllClustering, that use calcMembership to calculate community memberships and store them within the graph vertices attributes named after the algorithm. The difference between them is that calcAllClustering allows the user to calculate memberships for all clustering algorithms simultaneously (this can be slow, especially on larger graphs, e.g., up to 30 min for our full example network), and store them as graph vertices attributes, whereas calcClustering allows users to select a specific algorithm.
- g <- calcAllClustering(g)
- summary(g)
The resulting graph summary in the example will contain the graph memberships for all nine clustering algorithms: “fast-greedy community” (fc), “leading-eigenvector” (lec), “Walktrap” (wt), “SpinGlass” (sg), “Spectral” (spectral), “Louvain” (louvain), and “InfoMAP” (infomap). The SpinGlass algorithm is implemented as three instances (sgG1, sgG2, and sgG5), each based on a selected gamma value (1, 2, and 5, respectively) specifying the desired cluster size.
The user also has the option to select one or more specific clustering algorithm to run over their network, because running all clustering algorithms over the large network might be time consuming. For instance, to cluster the network g using only the Louvain algorithm, the command would look like:
- gl <- calcClustering(g, alg = “louvain”)
- summary(gl)
3.Compare the output of clustering algorithms.
For comparing output across different clustering algorithms on a network, a summary matrix is created, consisting of: the maximum modularity obtained (mod), the number of detected communities (C), the number of singlet communities (Cn1), the number of communities with size ≥100 (Cn100), the fraction of edges lying between communities (mu), the sizes of the smallest community (Min. C) and the largest community (Max. C), and the average (Mean C), median (Median C), first quartile (1st Qu. C), and third quartile (3rd Qu. C) of community size (Table 1).
- m <- clusteringSummary(g)
- View(m)
| Alg | mod | C | Cn1 | Cn100 | mu | Min. C | 1st qu. C | Median C | Mean C | 3rd qu. C | Max. C |
|---|---|---|---|---|---|---|---|---|---|---|---|
| lec | 0.339 | 16 | 3 | 8 | 0.526 | 1 | 5.25 | 102.5 | 143.5625 | 215.75 | 502 |
| wt | 0.2846 | 490 | 359 | 3 | 0.447 | 1 | 1 | 1 | 4.688 | 2 | 773 |
| fc | 0.394 | 20 | 0 | 6 | 0.390 | 2 | 5.25 | 22.5 | 114.85 | 105.25 | 565 |
| infomap | 0.379 | 174 | 0 | 2 | 0.597 | 2 | 6 | 8 | 13.201 | 14 | 125 |
| louvain | 0.425 | 15 | 0 | 11 | 0.479 | 22 | 101 | 121 | 153.133 | 216 | 311 |
| sgG1 | 0.448 | 24 | 0 | 9 | 0.440 | 2 | 5.75 | 11.5 | 95.708 | 231.5 | 316 |
| sgG2 | 0.433 | 42 | 0 | 8 | 0.523 | 3 | 10.75 | 56 | 54.690 | 71.5 | 158 |
| sgG5 | 0.368 | 102 | 0 | 0 | 0.617 | 3 | 14 | 22 | 22.520 | 27 | 78 |
| spectral | 0.370 | 63 | 9 | 4 | 0.595 | 1 | 3 | 28 | 36.460 | 56 | 184 |
-
Note that your own summary may look slightly different, as some of the algorithms use randomization, so each time they will give slightly (but not significantly) different results.
4.Visualize the community structure results.
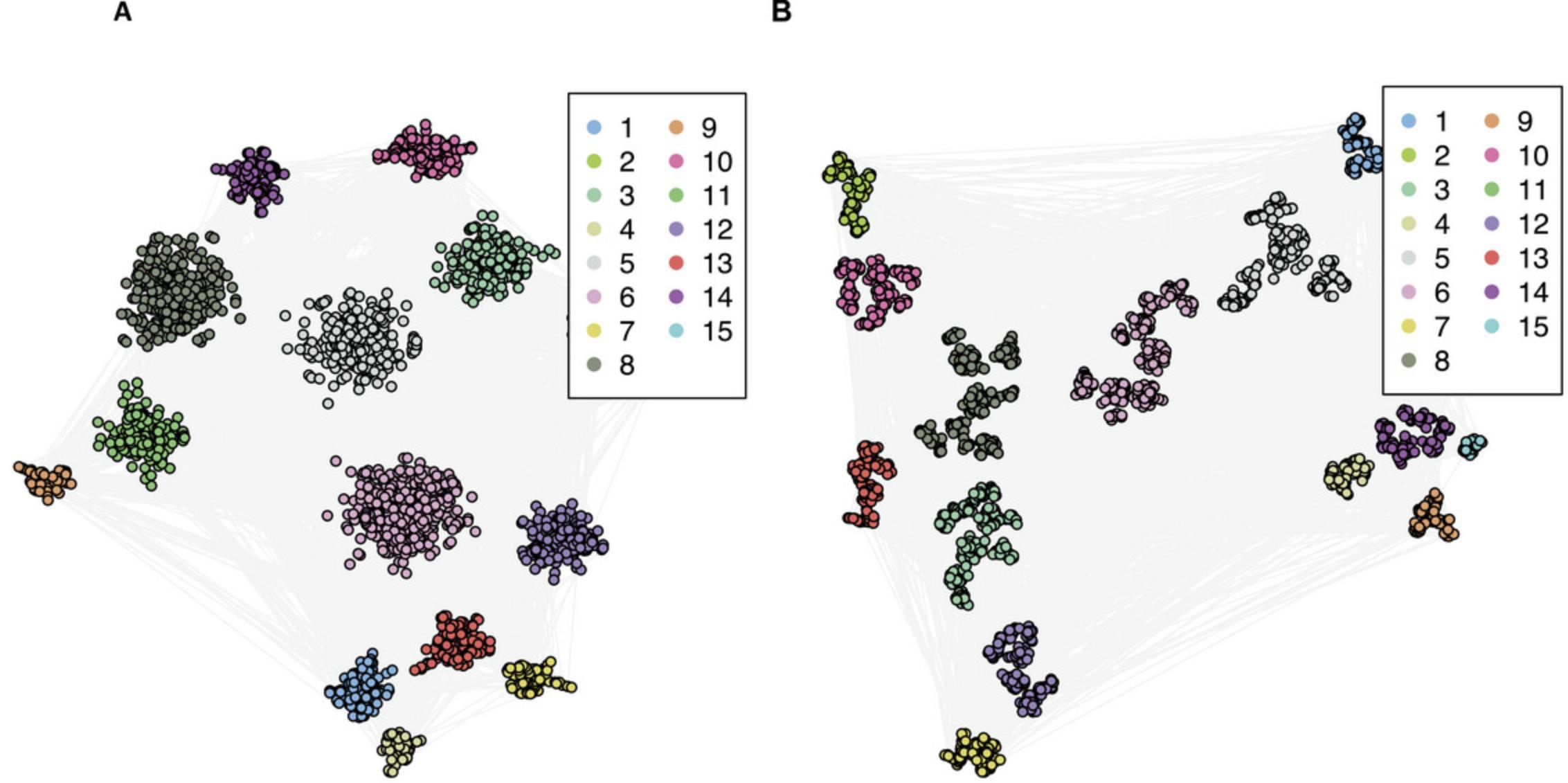
The BioNAR package provides functionality to visualize a network's community structure with an in-built cluster-driven layout algorithm, which is suitable for networks up to tens of thousands of vertices and millions of edges. This layout splits the network into clusters, lays out each cluster individually, and then combines individual layouts with the igraph function merge_coords, so that each distinct community is shown independently and painted in a unique color. In our example case, we show the community structure for the results obtained by the Louvain clustering algorithm, which resulted in 15 communities (see Table 1). For visualization purposes, we need to extract the membership in a form of a data frame. A palette is provided using distinctColorPalette command from the package randomcoloR, which defines an individual color for each community; the layoutByCluster command calculates the layout. Additionally, you can define edge color, size of the node, and position of the legend (Fig. 4A).
- library(randomcoloR)
- mem.df<-data.frame(names=V(g)
louvain)) - palette <- distinctColorPalette(max(as.numeric(mem.df$membership)))
- lay<-layoutByCluster(g,mem.df,layout = layout_nicely)
- plot(g,vertex.size=3,layout=lay, vertex.label=NA,
- vertex.color=palette[as.numeric(mem.df$membership)],edge.color='grey95')
- legend('topright',legend=names(table(mem.df$membership)),
- col=palette,pch=19,ncol = 2)
5.Re-cluster the obtained community structure (optional).
A common phenomenon when applying modularity-based clustering algorithms over networks of a large size is to end up with a small number of larger, or “super-,” communities, masking any substructures within these super-communities. In this situation, we provide the user with the facility to re-cluster these large/super-communities in a hierarchical manner, applying the same, or potentially a different, clustering algorithm at each iteration (re-cluster). We also need to specify the threshold for cluster size, which will be retained during re-clustering procedure—10 in our case—and then we use the same algorithm again.
- remem<-calcReclusterMatrix(g,mem.df,alg = “louvain”,10)
- head(remem)
This will return a table where each vertex name (1st column) will be assigned a cluster membership in the original graph (2nd column) and another cluster membership in the re-clustered graph (3rd column). In the example case of Louvain clustering results, the original clustered graph had 15 communities, and the re-clustered graph had 127.
6.Visualize the re-clustered community structure.
-
lay<-layoutByRecluster(g,remem,layout_nicely)
-
plot(g,vertex.size=3,layout=lay,
- vertex.label=NA,
- vertex.color=palette[as.numeric(mem.df$membership)],
- edge.color='grey95')
-
legend('topright',legend=names(table(mem.df$membership)),
-
col=palette,pch=19,ncol = 2)
The re-clustered graph is shown at Figure 4B.
Basic Protocol 4: IDENTIFYING THE OPTIMAL CLUSTERING ALGORITHM
The algorithms considered in Basic Protocol 3 are based on a range of different mathematical approaches and will give different results for the same network (as can be clearly seen in Table 1). However, for further analysis, presentation, or publication, it is usually necessary to select one clustered network model based on a single algorithm. In most cases, there is no ground truth, and the choice of the “correct” or “best” clustering algorithm is subjective. While accepting that there is no “correct” or “best” clustering approach, however, we can at least assess which algorithms identify “useful” clusters. To do this, we rely on an assumption that proteins/molecules that are well known to cooperate in the same complex/molecular pathways should be more likely to be found together in the same cluster. Thus, we can use our functional annotations (such as GO annotations) to help identify clustering methods that fit that assumption.
To achieve this, we estimate the number of enriched communities for each algorithm and for each annotation term, considering the network's size, the size of each cluster, and the number of annotated genes in the network and in the clusters (see Theoretical Appendix for background details that underpin the method).
The protocol starts by estimating the overrepresentation of annotation terms in each community discovered by each clustering algorithm. Overrepresentation analysis (ORA) is a common approach to identify annotation terms that are significantly over- or under represented in a given set of vertices compared to a random distribution. In biological networks, GO terms and pathway names are amongst the most frequently used. ORA differs from Gene Set Enrichment Analysis (GSEA) in that the latter use numerical values associated with genes, such as expression values, whereas the former relies on presence/absence data utilizing null hypothesis tests, such as the hypergeometric test. To keep the package as general purpose as possible, we used the Bioconductor package fgsea to implement ORA functionality on top of arbitrary string vertex annotation and vertex grouping, obtained by clustering (but not limited by it). We represent the results of ORA as an R data frame, with rows representing the combination of annotation term and cluster and columns—the enrichment characteristics, including the size of the cluster (Cn), the number of annotated vertices in the graph (Fn), the number of annotated vertices in the cluster (Mu), the odds ratio (OR) and its 95% confidence interval (defined by CIl and CIu), and the fold enrichment (Fe and FC). We also provide p -value, adjusted p -value, size of overlap, and the list of vertices from the cluster that contribute to the annotation term. Using the odds ratio allows us to distinguish functionally enriched communities relative to functionally depleted communities.
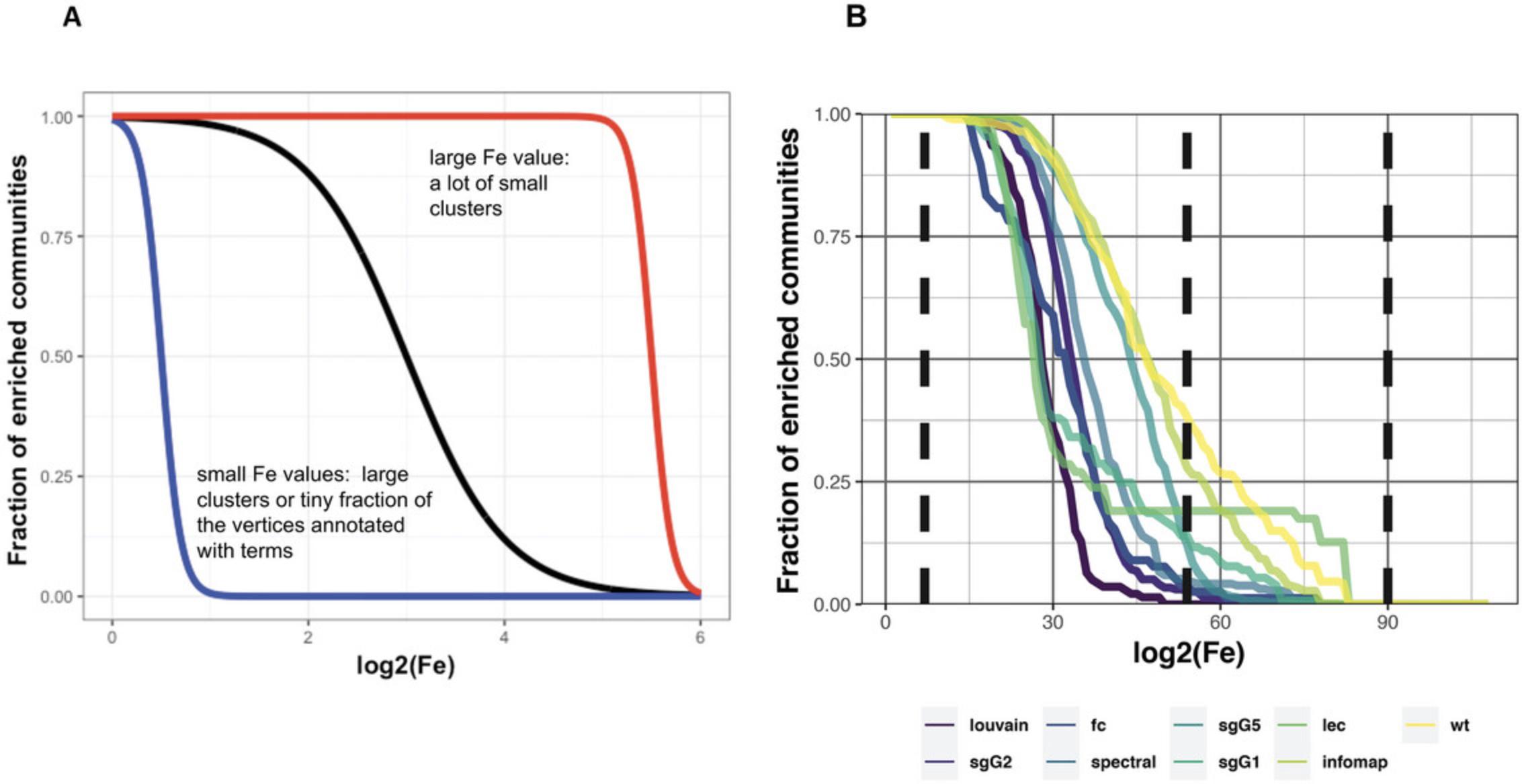
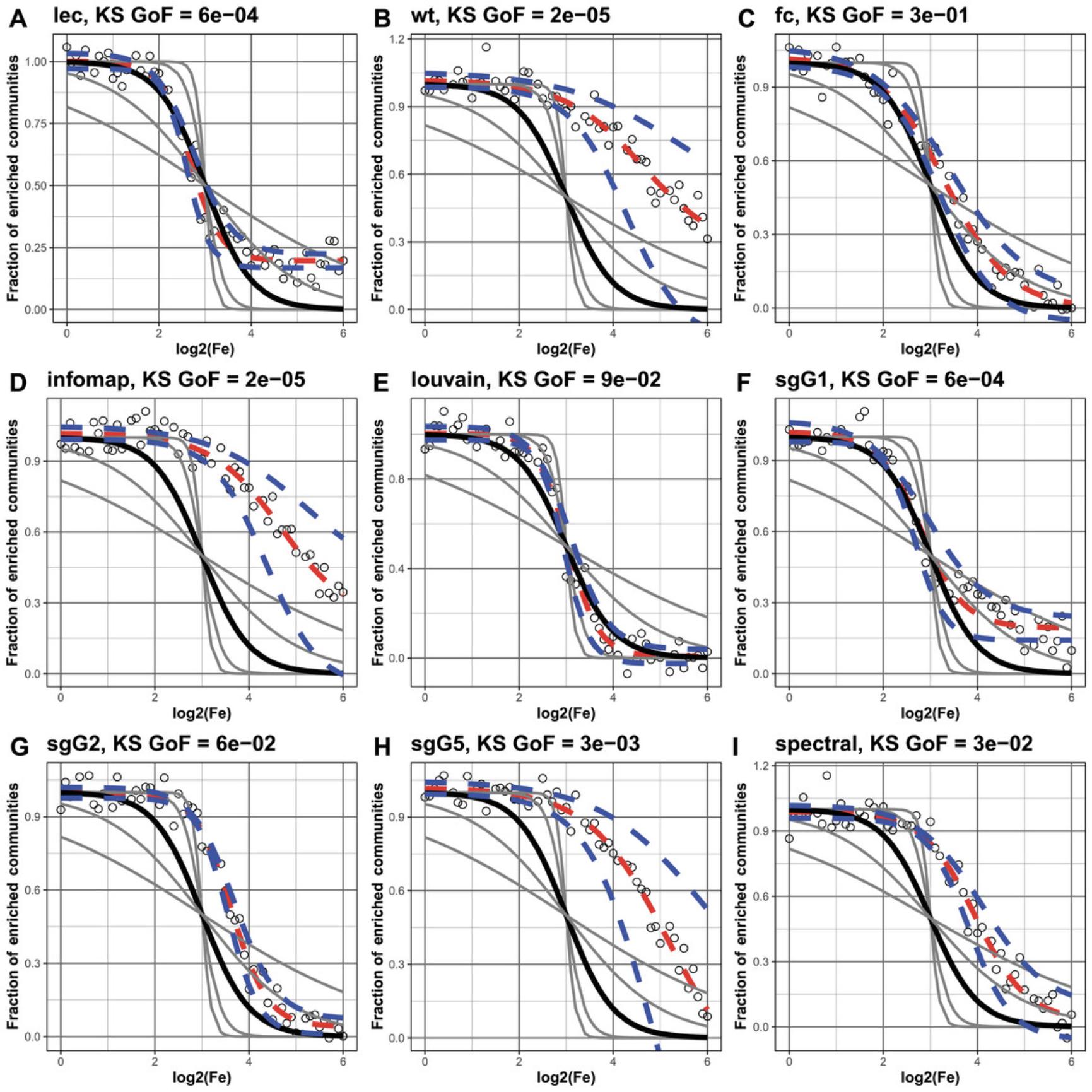
If we were to rank algorithms simply according to the percentage of functionally enriched communities, it would not tell us anything about the size of community the enrichment originates from—that is, whether the enrichment occurs within extremely large or small communities. Therefore, we plot the fraction of functionally enriched communities greater or equal to the log of its Fe value, measured at 100 intervals taken from 0 to the maximum Fe value (the maximum found from all algorithms studied). Because Fe values take into consideration the size of communities, at this step we can exclude enrichment from communities at the extreme sizes. In general, functional enrichment of non-extreme communities is observed by those clustering algorithms following a sigmoid distribution (see Fig. 5A). Thus, we test how well each distribution fits to a generalized sigmoid function using the two-sample Kolmogorov-Smirnov (KS) test to the goodness of fit of each distribution to our set of five idealized sigmoid curves (see Theoretical Appendix for technical detail).
To reproduce clustering results analyzed in this step, we recommend using the example network, built and stored in the external file PSD_annot_cls.gml in BioNAR. The network in this file is the same as in previous protocols but contains the clustering results already assigned to each node.
1.Load the network from BioNAR.
- file <- system.file(“extdata”, “PSD_annot_cls.gml”, package = “BioNAR”)
- gg <- igraph::read.graph(file,format=“gml”) #graph from gml
- summary(gg)
2.Estimate enrichment for the one clustering algorithm and one annotation.
If we want to take a look at overrepresentation for a specific algorithm, we need to select the algorithm and then use the function clusterORA to perform overrepresentation analysis for the results obtained with specified algorithm. We also need to specify the annotation set that we will use for assessing the clustering results. Here, we use GO Molecular function annotation (“GOMFID”), but it could be Biological Process or any other annotation, stored as a node attribute in our graph.
- ora<- clusterORA(gg, ‘louvain’, name = ‘GOMFID’,
- vid = “name”, alpha = 1, col = COLLAPSE)
3.Estimate enrichment for all selected clustering algorithms against the annotation set.
To compare all the clustering results, we need to select all algorithms that we want to compare. Then, using the function clusterORA, we perform the overrepresentation analysis on the results obtained with the specified algorithms. As before, we specify the annotation: GOMFID. Finally, we need to calculate FeMax, which corresponds to the maximum Fe value, and FcMax, which corresponds to the maximum Fc value. These values will be needed for further analysis to specify the required range of Fe and Fc values.
- algs<-c(‘lec’, ‘wt’, ‘fc’, ‘infomap’, ‘louvain’,
- ‘sgG1’, ‘sgG2’, ‘sgG5’, ‘spectral’)
- ora<-lapply(algs, function(alg){clusterORA(gg, alg, name = ‘GOMFID’,
- vid = “name”,alpha = 1, col = COLLAPSE)})
- names(ora)<-algs
- FeMax<-log2(max(sapply(ora,function(d){max(d$Fe)})))
- FcMax<-log2(max(sapply(ora,function(d){max(d$Fc)})))
4.Analyze unadjusted p -values for enrichment and print summary table (optional).
The command summaryStats will combine the results of enrichment obtained in the step 1, which will produce a list of tables: “SUM,” “SUM2,” “SUM3,” “SUM4,” and “CAN,” where the “SUM” table contains main summary that can be used for detailed analysis of algorithm/term pairs (which is outside the scope of this protocol) and “SUM2,” “SUM3,” and “SUM4,” containing the auxiliary values for further fitting to sigmoid curves.
The key table for the enrichment analysis is “CAN,” which records the annotation-term-to-cluster-association data for each clustering algorithm. This shows the user which clusters an enriched annotated term is associated with. As illustrated by the example below, “CAN” consists of four columns, where “ALG” corresponds to the name of the algorithm, “Fn” to the respective GO term ID, “C” to the ID of the cluster, and “Mu” to the number of the genes in the cluster annotated with this term (the cardinality of the pair; see Table 2 for the first six rows of the “CAN” table).
- statsR1 <- summaryStats(ora, 0.1, usePadj=FALSE, FeMAX=FeMax, FcMAX=FcMax).
- names(statsR1)
- View(head(statsR1$CAN))
| ALG | Fn | C | Mu |
|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-
ALG, algorithm name; Fn, enriched GO term ID; C, ID of enriched cluster; Mu, number of genes associated with a term.
5.Plot the fraction of enriched communities and rank the algorithms.
The command plotRatio creates a rank table for the algorithms and four plots, p1-p4, all showing the distribution of the fraction of enriched communities against fold enrichment (Fe). p1 and p3 show the distribution plotted against log2(Fe), whereas p2 and p4 use log(log2(Fe)). p1 and p2 highlight the top three distributions, whereas p3 and p4 (shown in Fig. 5B) plot all algorithms each with a different color. Table 3 and Figure 5B show that the Louvain algorithm gives the most useful distribution (for the example given), followed by sgG2 and fc.
- plots<-plotRatio(x=statsR1, desc=“p.values”,LEGtextSize=0.75, LEGlineSize=2)
- View(plots
p3)
| Alg | Fraction of communities enriched log2(FE) > 0.5_log2(FE) < 4.8 | Fraction of communities enriched log2(FE) > 4.8_log2(FE) < 8.0 |
|---|---|---|
| louvain | 1 | 0 |
| sgG2 | 0.973 | 0.027 |
| fc | 0.96 | 0.038 |
| spectral | 0.95 | 0.049 |
| sgG5 | 0.88 | 0.122 |
| sgG1 | 0.86 | 0.139 |
| lec | 0.81 | 0.190 |
| infomap | 0.72 | 0.279 |
| wt | 0.617857142857143 | 0.382142857142857 |
-
The table is obtained from the View(plots$ranktable) command.
6.Fit sigmoid function.
This command fits a sigmoid distribution (described in the Theoretical Appendix) to the fraction of enriched communities against Fe values for each clustering algorithm (Fig. 6). The function creates a list called fitres, which contains the fitting results. To visualize the fitting results, you need to print gridplot, which is the part of fitres.
- fitres<-fitSigmoid(statsR1)
- print(fitres[[‘0’]]$gridplot)
To view the fitting results, you will need to select fitInfo. They will be presented in the form of a table with the following columns: “alg,” corresponding to the algorithm's name; “isConv,” indicating whether the fit has converged; “finTol,” for the final fitting error; and “stopMessage,” providing a message describing the reason to stop fitting. You can also assess the results of two-sample Kolmogorov-Smirnov (KS) test by selecting “ks” below. Here the columns will correspond to the p -values from the Kolmogorov-Smirnov test of correspondence between Fe distribution and sigmoid function rates.
- View(fitres[[‘0’]]$fitInfo,caption = “Summary of the fitting results”)
- View(fitres[[‘0’]]$ks,caption = ‘Summary of the Kolmogorov-Smirnov test’)
![Details are in the caption following the image Results of fitting to five generalized sigmoid functions. Each panel, (A)-(I), illustrates a different clustering method. In each, four gray sigmoid curves correspond to four reference sigmoid curves with rate parameter c (see Technical Appendix) equal to [−10, −5, −1, −0.5], whereas the solid black sigmoid defines the ideal/desired behavior with rate equal to −2. The open circles and red line correspond to the actual fit, while the dashed blue line indicates the 95% confidence interval. Panels (C) and (E) show that the fc and Louvain algorithms give the closest fit to the ideal, with KS values of 1E-01 and 9e-02.](https://static.yanyin.tech/literature_test/cpz1940-fig-0006-m.jpg)
7.Test the robustness of obtained fitting results.
To test the robustness of the fit, we can add some noise to results obtained in previous step. We added noise to each data point by randomly sampling from a Gaussian distribution with mean 0 and a standard deviation of [0.01, 0.05, 0.1, 0.5]. For this we must specify the level of noise (here, 0.05) while executing the commands in step 4.The resulting fitting results with noise and values can be assessed in a similar way (Fig. 7). It can be seen that the fc, Louvain, and sgG1 algorithms give the more robust results.
- print(fitres[[‘0.05’]]$gridplot)
- View(fitres[[‘0.05’]]$fitInfo,align = ‘lllrrrl’,landscape = TRUE,
- main = ‘Summary of the fitting results’)
- View(fitres[[‘0.05’]]$ks,align = ‘lllrrrl’,landscape = TRUE,
- main = ‘Summary of the Kolmogorov-Smirnov test’)
We should note here that users should be cautious not use the same datasets (directly or indirectly) for generating the clustered network and testing it. In our example here, we used GO terms, which are not linked to the methods or datasets used in either the clustering methods or the construction of the network architecture, including selection of nodes and edges.
Basic Protocol 5: IDENTIFYING THE INFLUENTIAL PROTEINS WITH BRIDGENESS
Not all proteins act similarly in propagating signals, or information, through a network. It is often assumed that proteins that interact with many partners have more significant impact on signal propagation or on disease mechanisms when perturbed. It is also generally found that the majority of proteins interact with just a few neighbors, and thus their contribution is generally predicted to be less impactful (Vidal et al., 2011). The importance of a protein in propagating information appears to be dependent on its nearest neighbors, as well as its ability to influence other communities relative to the one to which it most likely belongs (Nepusz et al., 2008, 2012). The bridgeness metric reflects the probability that a vertex could belong to more than one community at the same time, thus providing a useful measure for ranking the vertices based on their topological influence and formation of linkages between clusters in the network model (Nepusz et al., 2008, 2012).
The protocol starts from the testing of the robustness of communities obtained in the “most useful” algorithm, obtained in Basic Protocol 3.For this, the consensus matrix is produced by creating smaller network by randomly keeping a proportion (by default 80%) of the network edges (type = 1) or vertices (type = 2) and rerunning the clustering algorithm on largest connected component of that network. This is then repeated (by default, 500 times) to produce a distribution (matrix) of clustered networks. This new matrix is used to estimate the bridgeness, which takes values between 0, implying that a vertex clearly belongs to a single community, and 1, implying that a vertex forms a “global bridge” across every community in the network with the same probability (Nepusz et al., 2008, 2012).
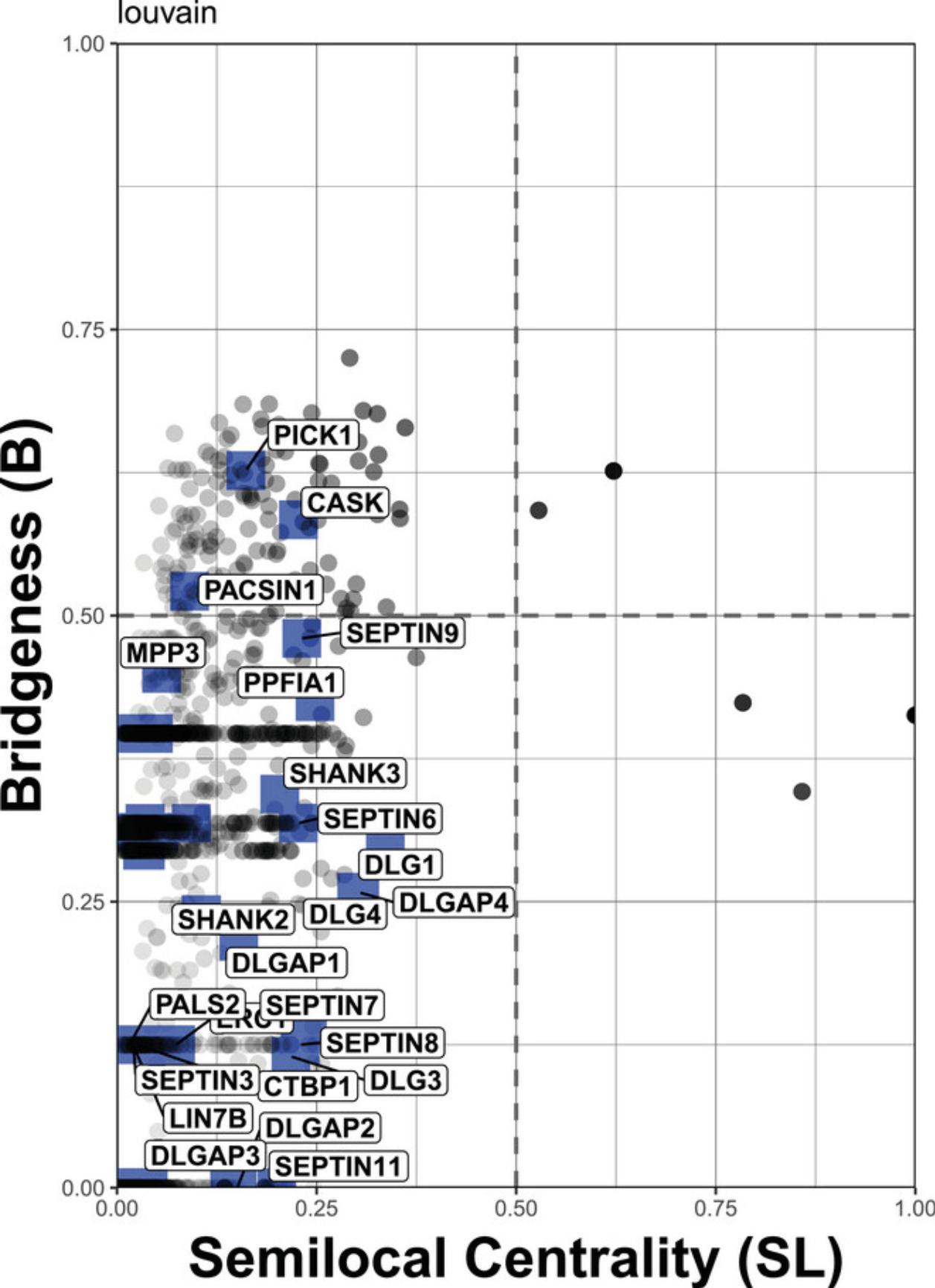
Although useful itself as a measure of a “global” network importance, bridgeness becomes more informative when combined with other vertex centrality measures, such as semi-local centrality. Semi-local centrality considers the nearest and next to the nearest vertex neighbors, so reflects the “local” importance of the protein. It also lies between 0 and 1 and indicates whether the vertex is likely to have local influence. Plotting bridgeness against semi-local centrality allows us to categorize both the local and global influence of each vertex within a network given only the network structure. BioNAR also supports the comparison of bridgeness against any vertex centrality measure (or any normalized numeric vertex value) of the user's choice, e.g., against page rank.
The protocol for this starts with estimating the bridgeness from the consensus matrix obtained in Basic Protocol 4 and proceeds by plotting the bridgeness against the centrality measure of choice, which is implemented in two ways. In this example, we continue working with the network from Basic Protocol 4 and the algorithm that showed the best enrichment performance there, i.e., Louvain.
1.First, calculate the consensus community structure:
-
conmat <- makeConsensusMatrix(g, N=5,
-
alg = “Louvain”, type = 2,
-
mask = 10, reclust = FALSE,
-
Cnmax = 10)
Here, “alg” selects the clustering algorithm to be used, “type” the sampling scheme (1 sample edges and 2 sample vertices) used, “mask” the percentage of edges or vertices to remove from the graph, “reclust” whether re-clustering should be performed on the community set found, “Cnmin” minimum cluster size, and “Cnmax” the maximum cluster size above which re-clustering will be performed (if reClust = TRUE). The resulting matrix conmat has dimensions of 2297 × 2297, where each matrix element is assigned the frequency with which a pair of nodes vertices is found in the same cluster.
2.Calculate the robustness of community structure. To do this, assign to each cluster a value in a range from 0, indicating no confidence in the community existing, to 1, indicating absolute confidence in the cluster existing, thus evaluating the “goodness” of a chosen clustering algorithm.
- clrob<-getRobustness(g, alg = “louvain”, conmat)
- pander(clrob)
This will return a 15 × 5 table, in which each of the 15 clusters obtain by the Louvain algorithm has the following values: C (cluster number), Cn (cluster size), Crob (cluster robustness), and CrobScaled (0-1, Crob after scaling). CrobScaled should be used to indicate cluster robustness. It can be seen in the example that the most robust cluster is Cl9 (CrobScaled = 1) and the least robust is Cl15 (CrobScaled = 0).
3.Calculate the bridgeness.
- br<-getBridgeness(gg,alg = “louvain”, conmat)
- head(br)
The command getBridgeness takes the graph and consensus matrix (conmat) from step 1 as an input and returns the bridgeness results in a form of table with three columns, where the first column contains ID (Human Entrez ID), the second GENE.NAME (Human Gene Name), and the third BRIDGENESS.louvain (bridgeness values obtained with the Louvain algorithm). Next, assign bridgeness values as vertex attributes:
- g<-calcBridgeness(g,alg = alg, conmat)
- vertex_attr_names(g)
For convenience, bridgeness values will also be stored as vertex attributes.
4.Plot bridgeness against the semilocal centrality (SL).
If we want to highlight the proteins of interest on the plot, we can specify their IDs as VIP vertices. In our case we will highlight the synaptic proteins with known function “Protein cluster,” based on a classification, extracted from an unrelated published study (Lips et al., 2012), which is also stored in BioNAR as an external data file.
- sfile<-system.file(“extdata”, “SCH_flatfile.csv”, package = “BioNAR”)
- shan<- read.table(sfile,sep=“\t”,skip=1,header=FALSE,strip.white=TRUE,quote=“”)
- head(shan)
The table shan consists of three columns: the first column contains the function number, the second the function description, and third the gene ID (Entrez ID) that is associated with this function. Here, we want to select gene IDs with “protein cluster” functions.
-
table(shan$V2)
-
shan[shan$V2 ==“Protein_cluster”,] -> prCl
-
dim(prCl)
-
plotBridgeness(g,alg = “louvain”,
-
VIPs=prCl$V3,
-
Xatt=‘SL’,
-
Xlab = “Semilocal Centrality (SL)”,
-
Ylab = “Bridgeness (B)”,
-
bsize = 3,
-
spsize =7,
-
MainDivSize = 0.8,
-
xmin = 0,
-
xmax = 1,
-
ymin = 0,
-
ymax = 1,
-
baseColor=“royalblue2”,
-
SPColor=“royalblue2”)
By plotting bridgeness against semi-local centrality (Fig. 8), we have categorized the influence each protein found in our network has on the overall network structure:
1.Region 1 (top left): Proteins with a “global” rather than “local” influence in the network (vertices in this region have also been referred to as bottleneck bridges, connectors, or kinless hubs; 0 < SL < 0.5; 0.5 < B < 1). 2.Region 2 (top right): Proteins with both “global” and “local” influence (0.5 < SL < 1, 0.5 < B < 1). 3. Region 3 (bottom left): Proteins centered within the community they belong to, but also communicating with a few other specific communities (0 < SL< 0.5; 0 < B < 0.5). 4.Region 4 (bottom right): Proteins with “local” impact, primarily restricted to just one or two communities (also referred to as local or party hubs; 0.5 < SL< 1, 0 < B < 0.5).
To plot the same figure in an interactive manner (to see the names for non-highlighted dots), the function ggplotly from the plotly library can be called as follows:
-
library(plotly)
-
gp<-plotBridgeness(g,alg = “louvain”,
-
VIPs= prCl$V3,
-
Xatt=‘SL’,
-
Xlab = “Semilocal Centrality (SL)”,
-
Ylab = “Bridgeness (B)”,
-
bsize = 1,
-
spsize =2,
-
MainDivSize = 0.8,
-
xmin = 0,
-
xmax = 1,
-
ymin = 0,
-
ymax = 1,
-
baseColor=“royalblue2”,
-
SPColor=“royalblue2”)
-
ggplotly(gp)
Basic Protocol 6: IDENTIFICATION OF OVERLAPPING ANNOTATIONS
This protocol describes how to identify which annotations overlap, and where within the network different annotations tend to overlap (or, conversely, are distinct and separate). For example, within large-scale molecular networks, disease-associated genes are often found closely linked to one another (referred to as disease modules by Menche et al., 2015, and based on the shortest path in the network linking the disease terms), and the composition of these modules can be compared across different diseases. Disease annotations that tend to overlap in these modules also tend to show significant similarities at the level of gene coexpression patterns, clinical phenotype, and comorbidity. Conversely disease annotations residing in separated network neighborhoods appear to be more phenotypically distinct.
This phenomenon is not restricted to diseases and can be generalized, so that given two annotations distributed across a network, a common query would be to find the points of intersection where the two annotation sets overlap (or segregate). To support such queries, we implemented the algorithm from Menche et al. (2015), which tests whether the observed mean shortest paths between two distinct annotation sets, superimposed on a network, is significant compared to a randomly annotated network.
The following example illustrates the estimation of disease separation for a manually selected set of diseases: DOID:10652 (Alzheimer's disease), DOID:3312 (bipolar disorder), DOID:14330 (Parkinson's disease), DOID:0060041 (autism spectrum disorder), DOID:1826 (epilepsy syndrome), DOID:5419 (schizophrenia), DOID:9255 (frontotemporal dementia), and DOID:1059 (intellectual disability). The command calcDiseasePairs estimates the separation of pairwise annotations across the graph and compares it with that of a randomly reannotated graph. This can be useful for generating a qualitative overview of the relationships between the annotations.
We do not need the cluster structure for this analysis, so the annotated network from Basic Protocol 2 (g) is sufficient to perform Basic Protocol 6.
1.Calculate the annotation pairs.
The BioNAR command calcDiseasePairs calculates the observed overlap between two annotation sets on a network, and compares this to a single instance of the network with annotations randomly permuted; this is useful for a qualitative estimate of how likely an overlap is simply a random occurrence.
To calculate annotation overlap, we need to specify the name of the annotations. In our example, it is TopOntoOVGHDOID, which contains the HDO IDs for diseases. We will also need to specify the IDs for which the overlap will be calculated. “r” corresponds to random permutations (other options are “none,” in which case no permutation will be applied at all, and “binned,” in which case the permutation process tries to take into account the node degree, which is slightly longer than random).
- p <- calcDiseasePairs(
- g,
- name = “ TopOnto_OVG_HDO_ID”,
- diseases = c(“DOID:10652”,“DOID:3312”, “DOID:14330”, “DOID:0060041”, “DOID:1826”, “DOID:5419”, “DOID:9255”, “DOID:1059”),
- permute = “r”
- )
- pander(p$disease_separation)
The command pander will return a snapshot of an 8 × 8 table, where for each of disease pair there is a value that ranges from negative (indicating potential overlap) to positive (indicating separation).
2.Calculate the significance of the annotation overlap.
To calculate the significance of observed overlaps (or separations) of the observed annotation pairs in the network, the command runPermDisease is used. This compares the overlap against multiple permutations of the network (where the user can define the number of permutations). Executing this command may take considerable time, depending on the number of permutations chosen. It generates a results table containing the overlap of each annotation pair with p -value, p adjusted by Bonferroni test, and q -value.
In our simple example below, we selected 100 permutations, but for better significance, there should be 10,000 permutations (requiring ∼1 hr of computing time for this size of network and this set of annotations).
-
r <- runPermDisease(
-
g,
-
name = “TopOnto_OVG_HDO_ID”,
-
diseases = c(“DOID:10652”, “DOID:3312”),
-
Nperm = 100,
-
alpha = c(0.05, 0.01, 0.001)
-
)
-
pander(r$Disease_overlap_sig)
The pander command will return a table containing a number of rows equivalent to the number of annotation pairs and the following columns: HDO.ID.A, the HDO ID for the first disease; N.A., the number of genes associated with this disease; HDO.ID.B, the HDO ID for the second disease; N.B., the number of genes associated with second disease; sAB, a value that characterizes the overlap (negative for overlap and positive for separation); Separated, indicating whether the pair is separated based on sAB; Overlap, indicating whether the pair overlaps based on sAB; zScore, the Z score for this pair of annotations (see the formula in Menche et al., 2015); p-value, the respective p -value for the overlap; Separation/Overlap.than.chance, indicating whether the ratio of the separation and overlap is greater than expected by chance; Bonferroni, the Bonferroni value for the overlap; p.adjusted, the p -value adjusted for multiple testing; and q-value, the q -value adjusted by the FDR. An example of the table resulting from this step is provided in the Supporting Information as Supplementary Table 1; in this table, a few pairs of diseases show significant overlap (highlighted in yellow), such as Alzheimer's disease and Parkinson's disease (p.adjusted = 6.01E-06, Bonferroni ***), schizophrenia and bipolar disorder (p.adjusted = 4.25E-013, Bonferroni ***), and autism spectrum disorder and bipolar disorder (p.adjusted = 5.51E-08, Bonferroni ***)
COMMENTARY
Background Information
Communication, or information transfer, between the components of a network is a common feature across many biological scales. Therefore, it is not entirely surprising that methods designed to analyze information flow in other types of networks have proven to be well suited to the analysis of biological networks. The analysis of social networks has proven to be a rich hunting ground for useful methods, from which many have translated well to the analysis of molecular interaction networks (Li et al., 2011; Ma & Zeng, 2003; Wunderlich & Mirny, 2006).
Many individual software tools have been developed to address the basic steps required for the type of analyses described above. For example, the igraph package in R supports building a network, estimating popular centrality measures, and several types of clustering (Gabor & Tamas, 2006). Cytoscape (Shannon et al., 2003), and its plug-ins support graphical representation and reconstruction of molecular networks and provide a number of approaches to extract interactions from a variety of sources—for example, the STRING interaction database (von Mering et al., 2003)—and perform clustering and estimation of the main centrality measures. Various other tools exist for functional enrichment analysis based on the GO, KEGG (Kanehisa & Goto, 2000), and Reactome (Gillespie et al., 2022) ontologies, such as the widely used DAVID package (Sherman et al., 2022), GOrilla (Eden et al., 2009), BiNGO (Maere et al., 2005), and GSEA (Subramanian et al., 2005), to name a few. The Bioconductor (Huber et al., 2015) package ClusterProfiler allows estimation of the annotation overrepresentation for the clusters within a network (Wu et al., 2021), and the fgsea package provides fast enrichment analysis against an arbitrary set of annotations (Korotkevich et al., 2021).
BioNAR combines the features above and adds new ones, reflecting the research the authors and their collaborators have been involved with in recent years. The methods presented here will work with any other similar type of graphical data. The protocols are described here for undirected graphs, but some of the methods will work fine on directed graphs, and incorporation of the graph directionality into package code is ongoing effort. The vertices are unweighted, although some methods will work on weighted graphs; however, the current package has not been tested on them. Finally, BioNAR does not currently delve into probabilistic graphical models. All three of these are avenues for future development, and as BioNAR is entirely open source, there are no restrictions on end-user customization or extension.
Critical Parameters
Users of these protocols should ensure that they are using a recent version of R and BioNAR. At the time of this writing, R (4.2.2) and BioNAR (1.2.0) are used.
Troubleshooting
Some potential errors and their respective solutions are presented in Table 4.
| Problem | Possible cause | Solution |
|---|---|---|
| No results are created in the environment by the command | There is typo or mistake in the command, such as the wrong argument name or a nonexistent variable. | Type the following: options(“show.error.messages”=TRUE) and repeat the command. R will give you meaningful description of the error. |
| The getEntropy function returns NaN in the UP and DOWN columns | The entropy calculation assumes a fully connected graph. In the case of disconnected graph, the entropy value is set to NaN. | Get the largest connected component of your network using gLCC<-findLCC(g) and repeat analysis with gLCC. |
| The getBridgeness function returns NaN in the UP and DOWN columns | The bridgeness calculation assumes a fully connected graph. In the case of disconnected graph, the entropy value is set to NA. | Get the largest connected component of your network using gLCC<-findLCC(g) and repeat analysis with gLCC. |
| Warning is issued: 1: In getClustering (gg, alg): Clustering calculations for algorithm … failed. NULL is returned. | Some clustering algorithms, in particular SpinGlass, assume a fully connected graph. In the case of a disconnected graph, a warning is shown, NULL is returned as a clustering result, and no membership attribute is added to the graph. | Get the largest connected component of your network using gLCC<-findLCC(g) and repeat analysis with gLCC. |
All functions in BioNAR have built-in help, accessible by typing ?function_name. In addition, documentation exists at http://www.qiime.org, and the help forum at http://forum.qiime.org is typically quite active and useful.
Understanding Results
Each of the protocols described here has been illustrated using a walk-through example from the mammalian synaptic proteome (see Fig. 1). In brief, we extracted a consensus list of proteins from a curated and published database of synaptic proteomics studies. We filtered the database to extract a list of proteins that were found in studies looking at the postsynaptic density in mouse, rat, or human and were reported by at least three different published studies. The same database also contains a curated list of direct protein-protein interactions between these proteins extracted from public databases.
Basic Protocol 1 walks the user through the initial generation of a network model containing vertices (proteins) and edges (protein-protein interactions). For your own network, you will need both these elements to build the network. One word of caution is that it is important to consider how well defined the interactions are: Are they based on direct molecule to molecule data? Many interaction databases comprise a mix of direct and indirect interactions, where indirect interactions mean that there may be undefined intermediate partners involved in the interaction between two species. These are factors that need to be considered depending on the application area. Alternatively, a model can be assembled using any other network package and saved in .gml format for import into BioNAR. The advantage of using BioNAR in this step is that it can be scripted for multiple instances of networks from larger datasets.
Basic Protocol 2 then provides a comprehensive suite of methods to analyze the network structure. The first of three subprocedures calculates a set of commonly used core network parameters that are generally used to assess whether the network looks real or could be contaminated with random noise (biological network models do typically contain at least some random noise). BioNAR offers two methods to measure how scale-free a network is, operating under the assumption that real biological networks tend towards a scale-free rather than a random architecture. One is based on comparing the observed network against a distribution of generated random networks of the same size and the other is based on measuring entropy within the network.
Basic Protocol 3 then applies a set of frequently used clustering algorithms to the raw network generated in Basic Protocol 1. BioNAR enables the use of a hierarchical approach to the network in which large (defined by user) clusters can be treated as networks in their own right and clustered again to dissect substructures within. Finally, the clustered network can be visualized graphically within BioNAR (Fig. 4), or alternatively a clustered network can be exported to be visualized in a package of choice.
Basic Protocol 4 considers the tricky problem of which clustering algorithm is “best.” There are few, if any, reliable ground truths, and clustering algorithms all behave differently as networks change in size and/or density of connections. Rather than call any algorithm “better,” we prefer the term “useful.” The basic concept here is that we usually do know something about the networks we are working on. In the case of protein interaction networks, there are well-known classic biochemical pathways, and the molecules within these pathways tend to share annotation terms in GO and generally directly interact with one another. Therefore, it is not unreasonable to expect these terms to be enriched within specific clusters, and indeed we do see this in clustered networks. BioNAR provides a suite of tools to compare across these networks and plot statistics that enable the user to assess how useful different clustering algorithms might be in terms of producing clusters that reproduce the small elements of prior knowledge we do have. Of course, any assessment based on optimizing enrichment will depend on the quality of the annotations used and how relevant they are to the biology. In all cases, it is vital to report exactly how a clustering algorithm was selected and share the raw network (e.g., from Basic Protocol 1) to allow others to try alternative algorithms.
Most clustering methods are based on a fundamental assumption that a node exists in exactly one cluster within the network. However, molecules can move, and they exist in in multiple copies, which permits different instances to be involved in different places at the same time. Further, the methods used to identify molecules or their interactions often lack full molecular resolution and identify a parent/canonical molecule rather than differentiating between all the variants expressed in a cell or tissue sample. As a partial move towards a more probabilistic network model, we incorporated bridgeness into BioNAR in Basic Protocol 5. By sampling the network and re-clustering multiple times, we can estimate how likely each molecule is to belong to each specific cluster. Although many vertices can be assigned fairly easily and are robust to perturbation, we find others that are much more susceptible to perturbation and may reflect molecules that are pleiotropic in their influence and interact with multiple pathways or molecular complexes. When we combine this measure with a local influencing metric, we can start to tease out molecules that are core to specific clusters versus molecules that have broad influence over the entire network.
Finally, we included Basic Protocol 6 to allow the users to examine relationships between annotations in the content of the network they have. This does not use the clustering in Basic Protocols 3-5 but rather builds off the initial annotated raw network in Basic Protocol 1. The results from this approach can provide fundamental insights into why annotation terms (such as genes associated with disease) often correlate despite there being no obvious similarity at the sequence level. When we overlay this onto the molecular interaction network, we can reveal where in the network these interactions occur and identify other molecules that are intimately associated with the correlation that might underpin a shared mechanism of disease. Put more simply, the molecules with shared function might be different at the sequence level but they tend to be close within the network. Conceptually this is the reverse of Basic Protocol 4.
Theoretical Appendix
The following provides a more detailed discussion of the technique's theoretical foundations but can be ignored by most readers. Readers without a strong computational background should be able to perform and understand the protocol without relying on this appendix.
Estimating entropy effects in the network
We test for evidence of structure in each network by performing an entropy-based perturbation analysis in a synthetically weighted network. In this analysis, the global entropy rate (SR) of the network is measured after each gene is individually perturbed, by either overexpression (SR_UP) or underexpression (SR_DOWN), and is plotted against the degree of the perturbed gene. To assign expression values to each vertex in the perturbation analysis, we followed Teschendorff et al. (2015) (implemented in BioNAR as a default procedure). Vertex weights are set to initial values of 2 and then sequentially perturbed to values of 14 when modeling activity, and are set to initial values of 16 with perturbed values of –14 when modeling inactively.
Comparing cluster enrichment to identify the optimal algorithm
The hypergeometric distribution was used to calculate the significance of enrichment of each cluster for each annotation (equation (1)):
where N is the total number of genes in the network, Cn is the number of genes in the community, F is the total number of functional annotated genes in the network, and μfc is the number of functional annotated genes per community.
Enrichment was calculated using equation (2), which gives us the one-sided exact Fisher test, and depletion was calculated using an alternative test given in equation (3).
The calculated p -values were corrected using the Benjamini and Yekutieli (B-Y) procedure (Benjamini & Yekutieli, 2001) and tested against the more stringent Bonferroni correction at the 0.05 (), 0.01 (), and 0.001 () significance levels.
Given the enrichment results, we can calculate the log of the odds ratio (OR) as:
and its upper and lower 95% confidence interval (CI) as:
where the terms are the same as those stated above.
The fold enrichment (Fe) value, measured at 100 intervals taken from 0 to the maximum Fe value (the maximum found from all algorithms studied), is estimated as follows:
where N is the total number of genes in the network, Cn is the number of genes in the community, F is the total number of functional annotated genes in the network, and μfc is the number of functional annotated genes per community.
For each algorithm, we measure the difference in fraction of enriched communities between log2(Fe) cut-off values of 0.5 (which translates to interval point 7 out of 100) and 4.8 (which is the interval point 54 out of 100).
Finally, we test how well each distribution is fitted to a generalized sigmoid function:
where a gives the sigmoid's lower asymptote, b the sigmoid's maximum value, c the sigmoid's rate of change, and d the × value of the sigmoid's midpoint. An ideal sigmoid for our case would occur when a = 0, b = 1, c = –2, and d = 3. Of the four parameters, it is the rate of change of the sigmoid curve that is of interest to us, as lower and upper asymptote are defined by nature of the fraction value as 0 and 1. To test how well each distribution (in Fig. 7) fit to a set of five ‘idealized’ sigmoid functions, with the other parameters fixed and c set to [–10, –5, 2, –1, –0.5], we apply the two-sample Kolmogorov-Smirnov (KS) test to the goodness of fit of each distribution to our set of five idealized sigmoid curves.
Acknowledgments
This research has received funding from the European Union's Horizon 2020 Framework Programme for Research and Innovation [no. 945539 (Human Brain Project SGA3)] and from Cancer Research UK [no. CTRQQR-2021\100006 (Cancer Research UK Scotland Centre)].
Author Contributions
Colin McLean : Conceptualization; formal analysis; investigation; methodology; software; validation; visualization; writing—review and editing. Anatoly Sorokin : Conceptualization; formal analysis; investigation; methodology; software; validation; visualization; writing—review and editing. J. Douglas Armstrong : Funding acquisition; methodology; supervision; writing—review and editing. Oksana Sorokina : Conceptualization; data curation; formal analysis; investigation; methodology; project administration; visualization; writing—original draft; writing—review and editing.
Conflict of Interest
The authors do not have conflicts of interest.
Open Research
Data Availability Statement
The package is available from Bioconductor release 3.17: https://bioconductor.org/packages/3.17/bioc/html/BioNAR.html
Supporting Information
cpz1940-sup-0001-SuppMat.txt
_Sample network file PSD_PPI.txt (_Basic Protocol Basic Protocol 1 ).
cpz1940-sup-0002-SuppMat.txt
_Sample network file PSDnetwork.gml (_Basic Protocol Basic Protocol 1 ).
cpz1940-sup-0003-SuppMat.gml
_Sample annotation file synGO.txt (_Basic Protocol Basic Protocol 1 ).
cpz1940-sup-0004-SuppMat.xlsx
_Sample table produced upon calculating the significance of the annotation overlap (_Basic Protocol Basic Protocol 6 , step 2).
Supporting Information
| Filename | Description |
|---|---|
| cpz1940-sup-0001-SuppMat.xlsx13.5 KB |
Please note: The publisher is not responsible for the content or functionality of any supporting information supplied by the authors. Any queries (other than missing content) should be directed to the corresponding author for the article.
Literature Cited
- Bánky, D., Iván, G., & Grolmusz, V. (2013). Equal opportunity for low-degree network nodes: A PageRank-based method for protein target identification in metabolic graphs. PLoS One , 8(1), e54204. https://doi.org/10.1371/journal.pone.0054204
- Barabasi, A. L., & Albert, R. (1999). Emergence of scaling in random networks. Science , 286(5439), 509–512. https://doi.org/10.1126/science.286.5439.509
- Benjamini, Y., & Yekutieli, D. (2001). The control of the false discovery rate in multiple testing under dependency. The Annals of Statistics , 29(4), 1165–1188. 1124. https://doi.org/10.1214/aos/1013699998
- Blondel, V., Guillaume, J., Lambiotte, R., & Lefebvre, E. (2008). Fast unfolding of communities in large networks. Journal of Statistical Mechanics: Theory and Experiment , 2008, P10008. https://doi.org/10.1088/1742-5468/2008/10/P10008
- Clauset, A., Newman, M. E., & Moore, C. (2004). Finding community structure in very large networks. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics , 70(6, Pt 2), 066111. https://doi.org/10.1103/PhysRevE.70.066111
- Eden, E., Navon, R., Steinfeld, I., Lipson, D., & Yakhini, Z. (2009). GOrilla: A tool for discovery and visualization of enriched GO terms in ranked gene lists. BMC Bioinformatics , 10, 48. https://doi.org/10.1186/1471-2105-10-48
- Erdös, P., & Rényi, A. (1959). On random graphs. Publicationes Mathematicae , 6, 290–297. https://doi.org/10.5486/PMD.1959.6.3-4.12
- Fernandez, E., Collins, M. O., Uren, R. T., Kopanitsa, M. V., Komiyama, N. H., Croning, M. D., Zografos, L., Armstrong, J. D., Choudhary, J. S., & Grant, S. G. (2009). Targeted tandem affinity purification of PSD-95 recovers core postsynaptic complexes and schizophrenia susceptibility proteins. Molecular Systems Biology , 5, 269. https://doi.org/10.1038/msb.2009.27
- Gabor, C., & Tamas, N. (2006). The igraph software package for complex network research. InterJournal Complex Systems , 1695.
- Gillespie, C. S. (2015). Fitting heavy tailed distributions: The poweRlaw package. Journal of Statistical Software , 64, 1–16. https://doi.org/10.18637/jss.v064.i02
- Gillespie, M., Jassal, B., Stephan, R., Milacic, M., Rothfels, K., Senff-Ribeiro, A., Griss, J., Sevilla, C., Matthews, L., Gong, C., Deng, C., Varusai, T., Ragueneau, E., Haider, Y., May, B., Shamovsky, V., Weiser, J., Brunson, T., Sanati, N., … D'Eustachio, P. (2022). The reactome pathway knowledgebase 2022. Nucleic Acids Research , 50(D1), D687–D692. https://doi.org/10.1093/nar/gkab1028
- P. D. Grünwald, I. J. Myung, & M. A. Pitt (Eds.). (2005). Advances in minimum description length theory and applications. MIT Press.
- Huber, W., Carey, V. J., Gentleman, R., Anders, S., Carlson, M., Carvalho, B. S., Bravo, H. C., Davis, S., Gatto, L., Girke, T., Gottardo, R., Hahne, F., Hansen, K. D., Irizarry, R. A., Lawrence, M., Love, M. I., MacDonald, J., Obenchain, V., Oleś, A. K., … Morgan, M. (2015). Orchestrating high-throughput genomic analysis with Bioconductor. Nature Methods , 12(2), 115–121. https://doi.org/10.1038/nmeth.3252
- Kanehisa, M., & Goto, S. (2000). KEGG: Kyoto encyclopedia of genes and genomes. Nucleic Acids Research , 28(1), 27–30. https://doi.org/10.1093/nar/28.1.27
- Klemmer, P., Smit, A. B., & Li, K. W. (2009). Proteomics analysis of immuno-precipitated synaptic protein complexes. Journal of Proteomics , 72(1), 82–90. https://doi.org/10.1016/j.jprot.2008.10.005
- Koopmans, F., van Nierop, P., Andres-Alonso, M., Byrnes, A., Cijsouw, T., Coba, M. T., Cornelisse, L. N., Farrell, R. J., Goldschmidt, H. L., Howrigan, D. P., Hussain, N. K., Imig, C., de Jong, A. P. H., Jung, H., Kohansalnodehi, M., Kramarz, B., Lipstein, N., Lovering, R. C., MacGillavry, H., … Verhage, M. (2019). SynGO: An evidence-based, expert-curated knowledge base for the synapse. Neuron , 103(2), 217–234. e4. https://doi.org/10.1016/j.neuron.2019.05.002
- Korotkevich, G., Sukhov, V., Budin, N., Shpak, B., Artyomov, M. N., & Sergushichev, A. (2021). Fast gene set enrichment analysis [Preprint]. BioRxiv , 060012. https://doi.org/10.1101/060012
- Li, M., Wang, J., Chen, X., Wang, H., & Pan, Y. (2011). A local average connectivity-based method for identifying essential proteins from the network level. Computational Biology and Chemistry , 35(3), 143–150. https://doi.org/10.1016/j.compbiolchem.2011.04.002
- Lips, E. S., Cornelisse, L. N., Toonen, R. F., Min, J. L., Hultman, C. M., Holmans, P. A., O'Donovan, M. C., Purcell, S. M., Smit, A. B., Verhage, M., Sullivan, P. F., Visscher, P. M., & Posthuma, D. (2012). Functional gene group analysis identifies synaptic gene groups as risk factor for schizophrenia. Molecular Psychiatry , 17(10), 996–1006. https://doi.org/10.1038/mp.2011.117
- Ma, H., & Zeng, A. P. (2003). Reconstruction of metabolic networks from genome data and analysis of their global structure for various organisms. Bioinformatics , 19(2), 270–277. https://doi.org/10.1093/bioinformatics/19.2.270
- Maere, S., Heymans, K., & Kuiper, M. (2005). BiNGO: A Cytoscape plugin to assess overrepresentation of gene ontology categories in biological networks. Bioinformatics , 21(16), 3448–3449. https://doi.org/10.1093/bioinformatics/bti551
- McLean, C., He, X., Simpson, I., & DJ, A. (2016). Improved functional enrichment analysis of biological networks using scalable modularity based clustering. Journal of Proteomics and Bioinformatics , 9(1), 9–18. https://doi.org/10.4172/jpb.1000383
- Menche, J., Sharma, A., Kitsak, M., Ghiassian, S. D., Vidal, M., Loscalzo, J., & Barabási, A. L. (2015). Disease networks. Uncovering disease-disease relationships through the incomplete interactome. Science , 347(6224), 1257601. https://doi.org/10.1126/science.1257601
- Nepusz, T., Petróczi, A., Négyessy, L., & Bazsó, F. (2008). Fuzzy communities and the concept of bridgeness in complex networks. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics , 77(1, Pt 2), 016107. https://doi.org/10.1103/PhysRevE.77.016107
- Nepusz, T., Yu, H., & Paccanaro, A. (2012). Detecting overlapping protein complexes in protein-protein interaction networks. Nature Methods , 9(5), 471–472. https://doi.org/10.1038/nmeth.1938
- Newman, M. E. J., & Girvan, M. (2004). Finding and evaluating community structure in networks. Physical Review E , 69(2), 026113. https://doi.org/10.1103/PhysRevE.69.026113
- Newman, M. E. (2006). Modularity and community structure in networks. PNAS , 103(23), 8577–8582. https://doi.org/10.1073/pnas.0601602103
- Pocklington, A. J., Armstrong, J. D., & Grant, S. G. (2006). Organization of brain complexity–synapse proteome form and function. Briefings in Functional Genomics & Proteomics, 5(1), 66–73. https://doi.org/10.1093/bfgp/ell013
- Pons, P., & Latapy, M. (2006). Computing communities in large networks using random walks. Journal of Graph Algorithms and Applications , 10(2), 191–218. https://doi.org/10.7155/jgaa.00124
- Reichardt, J., & Bornholdt, S. (2006). Statistical mechanics of community detection. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics , 74(1, Pt 2), 016110. https://doi.org/10.1103/PhysRevE.74.016110
- Rissanen, J. (1978). Modeling by shortest data description. Automatica , 14(5), 465–471. https://doi.org/10.1016/0005-1098(78)90005-5
- Rosvall, M., Axelsson, D., & Bergstrom, C. T. (2009). The map equation. The European Physical Journal Special Topics , 178, 13–23. https://doi.org/10.1140/epjst/e2010-01179-1
- Rosvall, M., & Bergstrom, C. T. (2008). Maps of random walks on complex networks reveal community structure. Proceedings of the National Academy of Sciences of the United States of America , 105(4), 1118–1123. https://doi.org/10.1073/pnas.0706851105
- Shannon, P., Markiel, A., Ozier, O., Baliga, N. S., Wang, J. T., Ramage, D., Amin, N., Schwikowski, B., & Ideker, T. (2003). Cytoscape: A software environment for integrated models of biomolecular interaction networks. Genome Research , 13(11), 2498–2504. https://doi.org/10.1101/gr.1239303
- Sherman, B. T., Hao, M., Qiu, J., Jiao, X., Baseler, M. W., Lane, H. C., Imamichi, T., & Chang, W. (2022). DAVID: A web server for functional enrichment analysis and functional annotation of gene lists (2021 update). Nucleic Acids Research , 50(W1), W216–W221. https://doi.org/10.1093/nar/gkac194
- Sorokina, O., Mclean, C., Croning, M. D. R., Heil, K. F., Wysocka, E., He, X., Sterratt, D., Grant, S. G. N., Simpson, T. I., & Armstrong, J. D. (2021). A unified resource and configurable model of the synapse proteome and its role in disease. Scientific Reports , 11(1), 9967. https://doi.org/10.1038/s41598-021-88945-7
- Sorokina, O., Sorokin, A., & Armstrong, J. D. (2022). Synaptome.db: A Bioconductor package for synaptic proteomics data. Bioinformatics Advances , 2, vbac086. https://doi.org/10.1093/bioadv/vbac086
- Subramanian, A., Tamayo, P., Mootha, V. K., Mukherjee, S., Ebert, B. L., Gillette, M. A., Paulovich, A., Pomeroy, S. L., Golub, T. R., Lander, E. S., & Mesirov, J. P. (2005). Gene set enrichment analysis: A knowledge-based approach for interpreting genome-wide expression profiles. Proceedings of the National Academy of Sciences of the United States of America , 102(43), 15545–15550. https://doi.org/10.1073/pnas.0506580102
- Teschendorff, A. E., Banerji, C. R., Severini, S., Kuehn, R., & Sollich, P. (2015). Increased signaling entropy in cancer requires the scale-free property of protein interaction networks. Scientific Reports , 5, 9646. https://doi.org/10.1038/srep09646
- Traag, V. A., & Bruggeman, J. (2009). Community detection in networks with positive and negative links. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics , 80(3, Pt 2), 036115. https://doi.org/10.1103/PhysRevE.80.036115
- Vidal, M., Cusick, M. E., & Barabasi, A. L. (2011). Interactome networks and human disease. Cell , 144(6), 986–998. https://doi.org/10.1016/j.cell.2011.02.016
- von Mering, C., Huynen, M., Jaeggi, D., Schmidt, S., Bork, P., & Snel, B. (2003). STRING: A database of predicted functional associations between proteins. Nucleic Acids Research , 31(1), 258–261. https://doi.org/10.1093/nar/gkg034
- Wu, T., Hu, E., Xu, S., Chen, M., Guo, P., Dai, Z., Feng, T., Zhou, L., Tang, W., Zhan, L., Fu, X., Liu, S., Bo, X., & Yu, G. (2021). clusterProfiler 4.0: A universal enrichment tool for interpreting omics data. Innovation , 2(3), 100141. https://doi.org/10.1016/j.xinn.2021.100141
- Wunderlich, Z., & Mirny, L. A. (2006). Using the topology of metabolic networks to predict viability of mutant strains. Biophysical Journal , 91(6), 2304–2311. https://doi.org/10.1529/biophysj.105.080572
- Zhu, X., Gerstein, M., & Snyder, M. (2007). Getting connected: Analysis and principles of biological networks. Genes & Development, 21(9), 1010–1024. https://doi.org/10.1101/gad.1528707

