A Comprehensive Guide for Assessing Covalent Inhibition in Enzymatic Assays Illustrated with Kinetic Simulations
Elma Mons, Elma Mons, Sander Roet, Sander Roet, Robbert Q. Kim, Robbert Q. Kim, Monique P. C. Mulder, Monique P. C. Mulder
Abstract
Covalent inhibition has become more accepted in the past two decades, as illustrated by the clinical approval of several irreversible inhibitors designed to covalently modify their target. Elucidation of the structure-activity relationship and potency of such inhibitors requires a detailed kinetic evaluation. Here, we elucidate the relationship between the experimental read-out and the underlying inhibitor binding kinetics. Interactive kinetic simulation scripts are employed to highlight the effects of in vitro enzyme activity assay conditions and inhibitor binding mode, thereby showcasing which assumptions and corrections are crucial. Four stepwise protocols to assess the biochemical potency of (ir)reversible covalent enzyme inhibitors targeting a nucleophilic active site residue are included, with accompanying data analysis tailored to the covalent binding mode. Together, this will serve as a guide to make an educated decision regarding the most suitable method to assess covalent inhibition potency. © 2022 The Authors. Current Protocols published by Wiley Periodicals LLC.
Basic Protocol I : Progress curve analysis of substrate association competition
Basic Data Analysis Protocol 1A : Two-step irreversible covalent inhibition
Basic Data Analysis Protocol 1B : One-step irreversible covalent inhibition
Basic Data Analysis Protocol 1C : Two-step reversible covalent inhibition
Basic Data Analysis Protocol 1D : Two-step irreversible covalent inhibition with substrate depletion
Basic Protocol II : Incubation time–dependent potency IC50(t)
Basic Data Analysis Protocol 2 : Two-step irreversible covalent inhibition
Basic Protocol III : Preincubation time–dependent inhibition without dilution
Basic Data Analysis Protocol 3 : Preincubation time–dependent inhibition without dilution
Basic Data Analysis Protocol 3Ai : Two-step irreversible covalent inhibition
Alternative Data Analysis Protocol 3Aii : Two-step irreversible covalent inhibition
Basic Data Analysis Protocol 3Bi : One-step irreversible covalent inhibition
Alternative Data Analysis Protocol 3Bii : One-step irreversible covalent inhibition
Basic Data Analysis Protocol 3C : Two-step reversible covalent inhibition
Basic Protocol IV : Preincubation time–dependent inhibition with dilution/competition
Basic Data Analysis Protocol 4 : Preincubation time–dependent inhibition with dilution
Basic Data Analysis Protocol 4Ai : Two-step irreversible covalent inhibition
Alternative Data Analysis Protocol 4Aii : Two-step irreversible covalent inhibition
Basic Data Analysis Protocol 4Bi : One-step irreversible covalent inhibition
Alternative Data Analysis Protocol 4Bii : One-step irreversible covalent inhibition
INTRODUCTION
Traditionally, drug design efforts were focused on small molecules that interact with their biological target through noncovalent interactions in a reversible manner. In contrast, covalent inhibitors have the ability to form a much stronger covalent bond with a nucleophilic amino acid residue at the target protein, which is positioned in close proximity to a reactive (electrophilic) moiety in the inhibitor (Ward & Grimster, 2021). Risks associated with covalent reactions that can take place not only with the desired target but also with off-target proteins, often undiscovered until late-stage clinical development, resulted in drug discovery programs moving away from candidates bearing intrinsically reactive electrophilic moieties (Bauer, 2015; Singh, Petter, Baillie, & Whitty, 2011). Nonetheless, the clinical success of covalent drugs that were being used in the clinic long before their mechanism of action was elucidated, which include aspirin and penicillin, along with the more recent clinical approval and success of targeted covalent inhibitors (TCIs) bearing moderately reactive electrophilic warheads, ultimately triggered the current resurgence of covalent drugs (Abdeldayem, Raouf, Constantinescu, Moriggl, & Gunning, 2020; De Cesco, Kurian, Dufresne, Mittermaier, & Moitessier, 2017; Singh et al., 2011).
The covalent inhibitor development process typically involves identification of noncovalent inhibitors by high-throughput screening (HTS), followed by modification with a moderately reactive electrophilic warhead to improve inhibition potency and selectivity (Engel et al., 2015; Zhang, Hatcher, Teng, Gray, & Kostic, 2019). Alternatively, an electrophilic fragment that forms a covalent bond with the desired enzyme target is first identified in covalent fragment–based drug discovery (Dalton & Campos, 2020; Kathman & Statsyuk, 2019; Resnick et al., 2019), followed by optimization of the noncovalent affinity and positioning of the electrophile. A prerequisite here is that the molecular target must contain a nucleophilic residue (e.g., cysteine, serine, lysine) to form a covalent bond with the electrophilic warhead of the inhibitor (Lagoutte, Patouret, & Winssinger, 2017; Ray & Murkin, 2019). Whether covalent adduct formation is reversible or irreversible depends on the selected electrophilic warhead (Bradshaw et al., 2015; Gehringer & Laufer, 2019; Lee & Grossmann, 2012; Shindo & Ojida, 2021). The PK-PD decoupling is one of the major advantages of irreversible inhibition: an infinite target residence time, resulting in a prolonged therapeutic effect after the inhibitor has been cleared from circulation (Abdeldayem et al., 2020; Barf & Kaptein, 2012; Gabizon & London, 2020; Kim, Hwang, Kim, & Park, 2021). Here, restoration of enzyme activity can only be achieved by de novo protein synthesis. At the same time, if the consequences of continued on-target inhibition are poorly understood, this same property can provide a safety concern. Consequently, inhibitors with a reversible covalent binding mode have become increasingly popular, with (tunable) target residence times ranging from several hours to multiple days (Bradshaw et al., 2015; Owen Dafydd et al., 2021; Serafimova et al., 2012).
Although traditional methods to evaluate inhibitor potency, such as determining half-maximal inhibitory concentration (IC50 values), are sufficient to identify hits in high-throughput screens, a more detailed kinetic evaluation is required to elucidate the structure-activity relationship (SAR) of irreversible covalent inhibitors (De Cesco et al., 2017; Harris et al., 2018; Holdgate, Meek, & Grimley, 2017). There are many extensive reviews on the history, development, and success of covalent inhibitors (Abdeldayem et al., 2020; De Cesco et al., 2017; Johnson, Weerapana, & Cravatt, 2010; Lagoutte et al., 2017), and experimental methods to assess undesired time-dependent inactivation (TDI) of CYP450 enzymes have been excellently reviewed (Stresser, Mao, Kenny, Jones, & Grime, 2014), but a comprehensive overview of experimental methods compatible with the desired covalent binding mode of TCIs targeting nucleophilic active-site residues has been missing. In the Strategic Planning section, we will introduce our customized set of interactive kinetic simulation scripts to study the kinetic concepts of different experimental methods, followed by a general background on (covalent) inhibitor binding modes, the assumptions on experimental enzyme activity assay conditions, and an introduction on time-dependent inhibitor kinetics. Our findings are discussed in detail in the section Experimental Methods and Data Analysis , where stepwise protocols are provided for four experimental methods with data analysis tailored to the different covalent binding modes. All are accompanied by an online available set of kinetic simulation scripts and troubleshooting guidelines, allowing readers to evaluate their covalent (ir)reversible inhibitor.
STRATEGIC PLANNING
This guide has been composed to aid readers that have identified an (ir)reversible covalent inhibitor and are contemplating which experimental method to select for the follow-up SAR analysis. Here, the performance of the enzymatic assay is not expected to be troublesome, but the challenge lies in the design of an assay method that complies with (often implied but not explicitly mentioned) assumptions on experimental conditions, and recognition of artifacts/errors in the interpretation of experimental outcome. As such, we assume that a functioning enzymatic assay with a robust read-out is already in place, and we will focus on the connection between (algebraic) data analysis methods and the respective assumptions on experimental conditions. It is important to note that this work is tailored to enzyme activity assays with a (fluorescence) read-out upon substrate processing to form a detectable product, and as such may not be compatible with other assay formats such as ligand binding competition assays or direct detection of the covalent enzyme-inhibitor adduct.
In the section ‘ Kinetic Simulations ’, we introduce the interactive kinetic simulation scripts used to illustrate the methods and kinetic concepts in this work. All figures are composed with in silico data generated in kinetic simulations, and can be recreated with the information in this section. The section ‘ Inhibitor Binding Modes ’ provides an overview of the (covalent) inhibition binding modes compatible with the methods in this work. It is paramount to select the appropriate algebraic model for data analysis, as the inhibitor binding mode changes the obtainable parameters as well as the compatibility with experimental methods. Covalent EI* adduct formation should be validated by direct detection with MS, X-ray crystallography or NMR (Harris et al., 2018; Liclican et al., 2020; Mons et al., 2019; Mons et al., 2021). Reversibility of covalent adduct formation is commonly assessed in rapid/jump dilution or washout assays with detection of regained enzymatic activity after dilution/washout (Copeland, Basavapathruni, Moyer, & Scott, 2011), MS detection of unbound inhibitor upon denaturation or digestion-mediated dissociation (Bradshaw et al., 2015), or competitive binding of a (selective) irreversible (activity-based) probe (Liclican et al., 2020; Smith et al., 2017). It is important to note that noncovalent binding can also irreversibly inhibit enzyme activity by aggregation or precipitation (Auld, Inglese, & Dahlin, 2017).
Next, we investigated which assumptions on experimental enzyme activity assay conditions are embedded in the algebraic models used for kinetic analysis. Our findings are outlined in the section ‘ Critical Parameters: Assumptions on Experimental Assay Conditions ’, highlighting which assumptions are crucial and what the consequences are when these assumptions are violated. Finally, we provide a kinetic background on time-dependent (covalent) inhibition in the section ‘ Time-dependent Inhibitor Potency ’. Readers new to the field of enzyme inhibition kinetics are strongly encouraged to familiarize themselves with the work of Copeland for a general introduction into enzyme kinetics (Copeland, 2000, 2013e) before studying advanced kinetic concepts associated with (ir)reversible covalent enzyme inhibition and their relation to experimental enzyme activity read-out.
Kinetic Simulations
Keeping assay requirements in mind, it may seem a daunting task to design, perform, and analyze proper inhibition experiments. In general, practice is the best teacher to get a feeling for these assays and the expected output. Kinetic simulations are essential to understand the importance of reaction conditions and support assay design optimization (Potratz, 2018). In such simulations, one can freely change the parameters to visualize the effect on the output and validate that kinetic parameters found after data analysis correlate with the input values. This design precludes assay artifacts and human error, and also outputs the underlying concentrations of the different reaction species (e.g., unbound enzyme, enzyme-substrate complex), illustrating the relevance of the experimental assay conditions. Finally, kinetic simulations can validate if fitted experimental parameters correlate with the experimental read-out (Pollard & De La Cruz, 2013) and aid the rational design of follow-up experiments by predicting the outcome.
Here, we use a set of customized kinetic simulation scripts based on numerical integration of the differential equations (Walkup et al., 2015) to simulate the time-dependent product concentration as well as the underlying concentrations of various enzyme species (e.g., unbound, bound to inhibitor or substrate). Some concentrations are essentially constant under specific assay conditions, and treating these parameters as constants rather than variables reduces the computing/simulation time. An overview of our kinetic scripts and the assumptions on experimental assay conditions can be found in Table 1. Since understanding kinetics can be greatly facilitated by the ability to adjust reaction conditions and changing parameters without using expensive reagents, we have made interactive versions of these simulation scripts available free of charge at https://tinyurl.com/kineticsimulations. We encourage our readers to perform simulations with their own kinetic parameters to visualize how the underlying concentrations of enzyme species affect the detected read-out, and to get a feeling for realistic values and assay conditions. We selected one model inhibitor for each binding mode to generate the figures that exemplify the methods described (the kinetic parameters of each model inhibitor can be found in Table S1 in Supporting Information). All figures in this work can be recreated with the information in Table 1 and Table S1.
- [I]0 = unbound inhibitor concentration at onset of inhibition, before (optional) enzyme binding. [I]t′ = unbound inhibitor concentration during preincubation, after (optional) enzyme binding. [I]t = unbound inhibitor concentration during incubation, after (optional) enzyme binding. [S]0 = unbound substrate concentration at onset of product formation, before enzyme binding. [S]t = unbound substrate concentration during incubation, after (optional) enzyme binding and product formation. Vt′ = reaction volume during preincubation. Vsub = volume containing substrate. Vt = reaction volume during incubation (Vt = Vsub + Vt′).
- a Available at https://tinyurl.com/kineticsimulations.
- b First-order spontaneous enzyme degradation/denaturation.
Our kinetic simulation scripts are tailored to competitive inhibition, where an intrinsically reactive inhibitor bearing an electrophilic warhead covalently targets a nucleophilic amino acid residue at the enzymatic substrate binding site, thus blocking substrate access (Copeland, 2013e; Holdgate et al., 2017). Other covalent binding modes [e.g., prodrugs (Strelow, 2017), covalent allosteric inhibitors (Lu & Zhang, 2017), and multi-step mechanism-based inhibitors (Tuley & Fast, 2018; Yang, Jamei, Yeo, Tucker, & Rostami-Hodjegan, 2005)] are outside the scope of this work, although the described experimental protocols can be useful in specific cases. For further instructions and detailed information on restrictions, we refer to the webpage itself.
At the start of the simulations, we define the (pre)incubation time. The preincubation time is the elapsed time since the onset of enzyme inhibition by mixing enzyme and inhibitor, but before the onset of product formation by adding substrate. The incubation time is the elapsed time since onset of product formation: after substrate addition. In this work, we will distinguish between incubation and preincubation by using different symbols for preincubation t′ (enzyme and inhibitor) and incubation t (enzyme, substrate and inhibitor) in all figures and equations to avoid confusion.
Inhibitor Binding Modes
Reversible noncovalent inhibitors inhibit enzymatic activity by formation of noncovalent EI complex in a single reaction step (Fig. 1A). When the initial unbound inhibitor concentration is equal to inhibition constant Ki, the concentration of unbound enzyme E will be equal to the concentration of inhibitor-bound enzyme complex EI after steady-state equilibrium has been reached. For traditional fast-binding reversible inhibitors this equilibrium will be reached almost instantly, as association rate constant k 3 and dissociation rate constant k 4 are fast. In this work, the term ‘reaction completion’ relates to the endpoint of enzyme-inhibitor binding, which refers to reaching an equilibrium for reversible inhibitors (Fig. 1A and 1B) or reaching full inactivation for irreversible inhibitors (Fig. 1C and 1D). Contrary to classic fast-binding inhibitors, time-dependent or slow-binding inhibition is observed when the steady-state equilibrium or irreversible inactivation is reached relatively slowly on the assay timescale (Copeland, 2013, 2013b, d). Typically, this is observed for inhibitors with a covalent binding mode (Fig. 1B-D), as formation of a covalent adduct is not an instantaneous process.
![Details are in the caption following the image Schematic overview of inhibitor binding modes (Tuley & Fast, 2018). E = unbound enzyme. I = unbound inhibitor. EI = noncovalent enzyme-inhibitor complex. EI* = covalent enzyme-inhibitor complex. An overview of kinetic constants can be found in Table S2 (see Supporting Information). Details on equilibrium constants are available in the Supporting Information. (A) Classic one-step reversible inhibition. Inhibitor potency ranking based on inhibition constant K<sub>i</sub> (M) or target residence time τ (s). (B) Two-step reversible covalent inhibition. Inhibitor potency ranking based on steady-state inhibition constant K<sub>i</sub>* (M) for total E + I <-> EI + EI* equilibrium or target residence time τ (s). (C) Two-step irreversible covalent inhibition (affinity label model). Inhibitor potency ranking based on inactivation efficiency: maximum rate of covalent adduct formation over inactivation constant k<sub>inact</sub>/K<sub>I</sub> (M<sup>−1</sup>s<sup>−1</sup>). (D) One-step irreversible covalent inhibition (residue-specific reagent model). Inhibitor potency ranking based on inactivation efficiency: k<sub>chem</sub> (M<sup>−1</sup>s<sup>−1</sup>) = k<sub>obs</sub>/[I] (M<sup>−1</sup>s<sup>−1</sup>).](https://static.yanyin.tech/literature_test/cpz1419-fig-0001-m.jpg)
Reversible covalent adduct formation (Fig. 1B) is a two-step process consisting of (rapid) initial association to form noncovalent EI complex (rapid equilibrium approximation , discussed in more detail in the section ‘ Critical Parameters: Assumptions on Experimental Assay Conditions ’) preceding covalent EI* adduct formation. Covalent EI* adduct is at equilibrium with the noncovalent EI complex, as covalent adduct formation is reversible (k 6 > 0), with inhibition constant Ki reflecting the initial noncovalent E + I <-> EI equilibrium and steady-state inhibition constant Ki* reflecting the steady-state (overall) E + I <-> EI + EI* equilibrium. Development of reversible covalent inhibitors typically involves optimization of overall affinity (reflected in low Ki* values), preferably by slowing dissociation rates (Fig. 1B). A slow off-rate (k off) is favorable, as this is reciprocal with the drug-target residence time τ (τ = 1/k off), and a longer residence time has been linked to superior therapeutic potency (Copeland, 2010; Copeland, Pompliano, & Meek, 2006). An overview of relevant kinetic parameters can be found in Table S2 (see Supporting Information).
Inhibition is considered irreversible when its residence time exceeds the normal lifespan of the target enzyme (Holdgate et al., 2017). Dissociation from covalent EI* adduct is negligible, resulting in full enzyme engagement when reaction completion is reached for irreversible covalent inhibitors (Fig. 1C and 1D). The irreversible binding mode changes the obtainable kinetic parameters to rank inhibitor potency, as the biochemical IC50 may vary depending on the (pre)incubation time (Holdgate et al., 2017; Singh et al., 2011). The potency of two-step irreversible inhibitors that engage in an initial noncovalent enzyme-inhibitor complex EI prior to formation of covalent adduct EI* is driven by noncovalent affinity reflected in inactivation constant KI along with the maximum rate of inactivation k inact (Fig. 1C). Rate constant k inact/KI is generally accepted as a more suitable measure of two-step irreversible inhibitor potency (Holdgate et al., 2017; Schwartz et al., 2014; Singh et al., 2011; Strelow, 2017), in an analogous fashion to k cat/KM reflecting the efficiency of enzymatic substrate conversion (detailed comparison can be found in Table S3 in Supporting Information). The binding mode becomes one-step when noncovalent equilibrium is non-existent, for example for highly reactive thiol-alkylating reagents (McWhirter, 2021; Strelow, 2017), with the parameter k chem or k obs/[I] reflecting potency/efficiency (Fig. 1D).
Drug development of irreversible covalent inhibitors is typically geared towards simultaneous improvement of the binding affinity (reflected in a lower KI value) and faster covalent bond formation (reflected in a higher k inact value) to generate irreversible covalent inhibitors with a high k inact/KI value for the desired enzyme target (Mah, Thomas, & Shafer, 2014; Schwartz et al., 2014), while minimizing the intrinsic reactivity with undesired enzymes such as GSH (Guan, Williams, Pan, & Liu, 2021; Lonsdale et al., 2017; Martin, MacKenzie, Fletcher, & Gilbert, 2019). Typical reported k inact/KI values of irreversible inhibitors range from 105-107 M−1s−1 for kinase inhibitors (Schwartz et al., 2014; Telliez et al., 2016; Zhai, Ward, Doig, & Argyrou, 2020), 101-105 M−1s−1 for protease inhibitors (Meara & Rich, 1995; Mons et al., 2019; Rocha-Pereira et al., 2014), 102-104 M−1s−1 for other target classes (Fell et al., 2020; Hansen et al., 2018; Lanman et al., 2020), to 10−2-102 M−1s−1 for covalent fragments (Johansson et al., 2019; Kathman, Xu, & Statsyuk, 2014). Ranges of clinically relevant k inact/KI values are highly dependent on the nucleophilicity of the targeted amino acid (cysteine typically being more reactive than serine) and concentration of naturally present competitors (e.g., ATP-competitive inhibitors need to overcome competition by ATP at physiological concentrations far exceeding the KM,ATP).
Critical Parameters: Assumptions on Experimental Assay Conditions
Experimental conditions should meet certain criteria in order to use algebraic fitting methods. In this paragraph, we focus on the assumptions (Michaelis – Menten Enzyme Kinetics , Enzyme Stability, Constant Uninhibited Product Formation Velocity , Rapid Equilibrium Approximation , Pseudo First-order Reaction Kinetics without Inhibitor Depletion) on the experimental conditions that are embedded in algebraic equations to analyze time-dependent (covalent) inhibition. Generally, these assumptions involve simplifying the enzyme-inhibitor binding reaction to a single rate-determining step along with fixing inhibitor/substrate concentrations to a constant value. There are two distinct types of algebraic analysis: linear regression (fitting straight curves, compatible with commonly available software such as Excel) and nonlinear regression (fitting exponential curves, requiring sophisticated data fitting software). Linear regression was the predominant method to analyze kinetic data, but has now been surpassed by the more accurate nonlinear regression (Perrin, 2017). For our analyses, we use least-squares nonlinear regression with GraphPad Prism (RRID:SCR_002798), but other software packages are available too (Rufer, 2021). Please consult the detailed (online) guide on how to implement user-defined equations for nonlinear regression in GraphPad Prism (Motulsky & Christopoulos, 2003; also see Internet Resources section at end of article).
To use algebraic fitting, the experiment should meet all the required conditions outlined below. More complex systems (such as bisubstrate assay or other binding modes like allostery) violate one or more of these and require a different method of fitting. For such systems, numerical integration with dedicated software packages [e.g., KinTek (Johnson, 2009), DynaFit (Kuzmič, 2009)] is recommended. These packages are very powerful, and can fit anything with good error even when the model does not reflect the biological situation (Mayer, Khairy, & Howard, 2010). For these complex systems, it is crucial to ensure that the initial values are reasonable and the amount of (orthogonal) data is sufficient for the amount of parameters that are fitted. The first step, however, whether working with complex systems or reactions with a single rate-determining step, should always be optimization of the experimental conditions.
Michaelis–Menten enzyme kinetics
All experimental methods in this manuscript are based on enzyme activity assays with multiple turnovers per enzyme, with enzyme release after product formation. We assume that the uninhibited enzymatic substrate processing reaction (E + S <-> ES → E + P) complies with Michaelis–Menten enzyme kinetics (Pollard & De La Cruz, 2013; Rufer, 2021). The concentration of unbound substrate has to be constant ([S]t = [S]0) and not depleted by engagement in a (non)covalent complex ES ([ES]t < 0.1[S]0) or conversion into product. Therefore, substrate is added in a large excess over the enzyme ([S]0 > 10[E]0), and the uninhibited velocity of product formation (vctrl) is calculated over the linear part corresponding to less than 10% substrate conversion ([P]t < 0.1[S]0) (Wu, Yuan, & Hodge, 2003). The signal corresponding to 10% substrate conversion can be estimated from a product calibration/titration curve (Dharadhar et al., 2019; Janssen et al., 2019) to avoid substrate depletion. The effect of substrate depletion can be investigated with the kinetic simulation script KinSubDpl. More complex enzymatic (bisubstrate) assays (Copeland, 2000) are outside of the scope of this work. However, the methods described herein could still be applicable under pseudo-single substrate (Hit-and-Run) conditions.
Enzyme stability
Unless otherwise noted, time-dependent decrease of enzyme activity is attributed solely to the presence of a (slow-binding) inhibitor. It is thus assumed that the enzyme activity is constant throughout the whole experiment, although this does not necessarily reflect the actual experimental situation. Recombinant enzymes do not have an eternal life; thus, time-dependent loss of enzyme activity will inevitably occur due to spontaneous protein denaturation, degradation, or unfolding (Miyawaki, Kanazawa, Maruyama, & Dozen, 2017). The Selwyn test is a relatively simple test to see if time-dependence of uninhibited enzyme activity is due to (spontaneous) enzyme inactivation (Selwyn, 1965). Spontaneous enzyme degradation/denaturation is similar to radioactive decay in a sense that inactivation is a first-order reaction (degradation rate = k degE×[E]). Enzyme stability might be promoted by optimization of the assay buffer, and is less significant at shorter (pre)incubation times, but degradation cannot completely be avoided. Therefore, we included data analysis methods to account for spontaneous first-order enzyme degradation/denaturation. Cannibalistic proteases (Ferrall-Fairbanks, Kieslich, & Platt, 2020) follow a second-order (auto)proteolysis rate (degradation rate = k degE×[E]2) and are as such outside of the scope of these methods. In simulations to illustrate the methods described herein (with kinetic simulation scripts KinDeg and KinVolDeg), we assumed that first-order decay is uniform for all enzyme species (k degE = k degES = k degEI = k degEI*) and combined the individual degradation rates into the enzyme degradation rate constant k deg.
Constant uninhibited product formation velocity
The uninhibited controls should be linear for the whole measurement when analyzing time-dependent inhibition. There are various factors contributing to a slight time-dependent decrease of product formation velocity in the absence of inhibitor (Copeland, 2000), thus violating this assumption. An overview of common troubleshooting options is listed in Table 3 (located in the troubleshooting section at the end of this document). As discussed above, substrate depletion ([P] > 0.1[S]0) negatively influences the linearity over time, as does product inhibition ([P] > 0.1KD,P). Fortunately, this can be avoided by decreasing the enzyme concentration and/or shortening the incubation time to reduce substrate turnover, thereby lowering the absolute and relative product concentration. Other factors, such as quenching of the fluorescent product signal by photobleaching (Johnson, 2010), can make the results look nonlinear. This effect can be reduced by increasing the measurement interval and/or reducing the number of excitation cycles. Finally, optimization of assay conditions can minimize the effect of spontaneous loss of enzyme activity (k deg > 0), but cannot be resolved completely. In this work, we will refer to the overall rate of nonlinearity in the uninhibited control (k obs of [I] = 0) with the symbol k ctrl, regardless of the underlying mechanism that causes the time-dependent decrease of product formation velocity.
Rapid equilibrium approximation
Algebraic analysis of (covalent) inhibition is based on the assumption that time-dependent inhibition is driven by a single rate-determining step. For two-step covalent inhibitors (Fig. 1B and 1C), this means that the noncovalent E + I <-> EI equilibrium that precedes covalent EI* adduct formation should be reached almost instantly after the onset of inhibition. After this rapid equilibrium, a much slower step of covalent adduct formation follows (k inact << k 4). Whether the noncovalent equilibrium indeed is reached rapidly is an intrinsic inhibitor property, and (kinase) inhibitors with a low-nM noncovalent potency are likely to violate this assumption: the association rate constant is diffusion-limited (k 3 ≤ 109 M−1s−1), and thus k 4 must be relatively slow if Ki ≤ 10-8 M (Kuzmič, 2020a). Unfortunately, a slow initial, noncovalent step is not easily recognized from raw kinetic data, resulting in overestimation of the rate of inactivation k inact and underestimation of the inactivation constant KI with algebraic rather than numerical data analysis.
The inactivation constant KI approximates inhibition constant Ki (KI ≈ Ki) when covalent bond formation is driven by the rate-determining conversion of noncovalent complex EI into covalent adduct EI* (k inact << k 4) (Fig. 1C), analogous to the Briggs–Haldane treatment of enzyme-substrate kinetics where KM ≈ KS if k cat is rate-limiting (McWhirter, 2021). Consequently, Ki and KI may have the same value, but they are not interchangeable, and it is as such recommended to report k inact/KI rather than k inact/Ki.
Pseudo first-order reaction kinetics without inhibitor depletion
Algebraic analysis of (covalent) inhibition is typically based on the assumption that the unbound inhibitor concentration is a constant value ([I]t = [I]0) unaffected by enzyme binding (Pollard & De La Cruz, 2013). This assumption is only valid when the inhibitor is present in large excess with respect to the enzyme ([I]0 > 10[E]0) at reaction initiation. The enzyme occupancy after reaching the noncovalent equilibrium is driven solely by the excess inhibitor concentration relative to the (apparent) inhibition constant Kiapp: [EI]eq/[E]0 = 1/(1 + (Kiapp/[I])). The effect of inhibitor depletion can be investigated with the kinetic simulation script KinInhDpl. Violation of this assumption results in an appreciable reduction of the remaining population of unbound inhibitor upon complexation with enzyme. Consequently, the inhibitor occupancy at equilibrium no longer reflects the apparent inhibition constant Kiapp because the equilibrium is now driven by both enzyme and inhibitor concentration (Fig. 2A). Algebraic correction for inhibitor depletion ([I]t < [I]0) to find the equilibrium constant Ki is often performed for one-step reversible inhibitors displaying tight-binding behavior (with low inhibitor concentrations because Kiapp approaches [Etotal]), by fitting the (steady-state) equilibrium product formation velocity to (variants of) Morrison's quadratic equation (Copeland, 2013c; Murphy, 2004) that treat the inhibitor concentration as a variable rather than a constant value (more details in Supporting Information). However, these equations are only compatible with inhibitors with a reversible binding mode after equilibrium has been reached, and are thus not suitable for irreversible inhibition.
![Details are in the caption following the image Consequences of inhibitor depletion. Simulated with KinInhDpl for 50 nM inhibitor C with 5 nM enzyme ([I]<sub>0</sub> = 10[E]<sub>0</sub>) or 50 nM enzyme ([I]<sub>0</sub> = [E]<sub>0</sub>). (A) Inhibitor depletion (blue line) results in lower noncovalent equilibrium occupancy [EI]<sub>eq</sub> calculated with Morrison's quadratic equation (available in Supporting Information) and slower reaction rates resulting in longer incubation time to reach full inactivation than for excess inhibitor (black line). (B) First-order reaction conditions with constant half-life t½ when inhibitor is present in excess (left). Second order reaction conditions with variable half-life t½ and longer overall reaction time when inhibitor is depleted (right).](https://static.yanyin.tech/literature_test/cpz1419-fig-0002-m.jpg)
Binding of inhibitor to enzyme is, in principle, a second-order reaction: the association rate depends on the concentration of unbound enzyme as well as unbound inhibitor, which both decrease upon formation of association product EI. Towards the end of the reaction, the reaction rate is significantly slower when less of the unbound components are left. Algebraic analysis of second-order (ir)reversible association curves is complicated (data not included, simulated with simulation script KinInhDpl), even for inhibitors with a one-step binding (Fig. 1); thus, it is strongly advised to analyze second-order reactions of two-step (ir)reversible inhibitors by numeric integration (Copeland, 2013a). However, as mentioned above, unbound inhibitor concentrations remain more or less constant during the reaction if the inhibitor is present in excess at reaction initiation ([I]0 > 10[E]0). Consequently, the second-order binding reaction of enzyme and inhibitor behaves like a first-order reaction when the inhibitor is present in excess: pseudo-first order reaction kinetics (Copeland, 2013a). The time-dependent association reaction for a (pseudo-)first order reaction has a constant half-life t½, and the progress curves can be fitted to standard one-phase exponential association equations (Fig. 2B, left), as will be discussed in more detail in the next section.
Second-order kinetic association reactions require a longer overall time to reach reaction completion of the enzyme-inhibitor binding reaction (inactivation or equilibrium) with a variable half-life t½ (Fig. 2B, right), because the association reaction rate slows down when the remaining unbound inhibitor concentration decreases. For two-step (ir)reversible inhibitors, the time-dependent reduction in covalent reaction rate is a direct consequence of the decreasing noncovalent occupancy upon inhibitor depletion. The rate-determining step of covalent adduct formation is preceded by noncovalent complex EI formation, and is thus limited by noncovalent occupancy, which decreased over time.
Time-Dependent Inhibitor Potency
Methods to analyze time-dependent inhibitors are based on the fact that it takes time to reach completion, and we use this information to obtain kinetic parameters. Under pseudo-first-order conditions (Copeland, 2013a) based on a single rate-determining step, inhibitor binding follows an exponential one-phase association reaction (Pollard & De La Cruz, 2013) from the rapid initial binding (rapid equilibrium approximation) to (slowly) reaching a plateau at reaction completion : equilibrium for reversible inhibitors (Fig. 3A, right) or inactivation for irreversible inhibitors (Fig. 3A, right). The incubation time to reaction completion is infinite, but after five half-lives (t = 5t½) reaction progress is at 97%, which is generally sufficient to be considered reaction completion (Fig. 3A). Reaction half-life t½ is inversely related to observed reaction rate k obs (Copeland, 2013a): t½ = LN(2)/k obs. k obs is the experimental reaction rate for reaction progress from initial binding to reaction completion under the specific assay conditions. Inhibitor concentration as well as competing substrate concentration are major contributors to the observed reaction rate k obs. The experimental k obs value can be obtained by fitting the time-dependent binding/occupancy curve to exponential one-phase association Equation I (Fig. 3B) from initial to final enzyme occupancy.
![Details are in the caption following the image Time-dependent Inhibition and Reaction Completion. Simulated with KinGen for 1 pM enzyme with substrate S1. (A) Time-dependent enzyme occupancy simulated for 50 nM one-step reversible inhibitor A (left) or two-step irreversible inhibitor C (right) in presence of 100 nM substrate S1. Each half-life t½, the occupancy increases by 50% (of the remaining span). After 5t½, occupancy is at 97% of its maximum (equilibrium concentration [EI]<sub>eq</sub> or total enzyme concentration [E]<sub>0</sub>) and generally considered as reaction completion. Half-life t½ is inversely related with observed reaction rate k<sub>obs</sub> (under pseudo-first order conditions). (B) Bounded exponential association Equation I from initial occupancy (rapid equilibrium) to final occupancy (reaction completion). (C) Progress curve of time-dependent product formation for enzyme inhibition in Figure 3A. Product formation velocity (slope, in AU/s), reflecting the (remaining) enzyme activity decreases until reaction completion is reached (steady-state equilibrium or inactivation). (D) Exponential association Equation II from initial velocity v<sub>i</sub> (rapid equilibrium) to final velocity v<sub>s</sub> (reaction completion). (E) k<sub>obs</sub> curves in absence (black, [S] = 0) or presence (gray, [S] = 2K<sub>M</sub>) of competing substrate. Apparent values are not yet corrected for substrate competition. (F) Two-step irreversible covalent inhibitors display one-step behavior at non-saturating inhibitor concentrations ([I] ≤ 0.1K<sub>I</sub>). Fit straight line with Y-intercept = k<sub>ctrl</sub> to obtain k<sub>chem</sub> = (k<sub>inact</sub>/K<sub>I</sub>) from the linear slope. (G) Two-step irreversible covalent inhibitors display one-step behavior at saturating inhibitor concentrations ([I] > 10K<sub>I</sub>). Distinguish from non-saturating inhibitor concentrations in Figure 3F: Y-intercept > k<sub>ctrl</sub> when fitting a straight line to the k<sub>obs</sub> curve.](https://static.yanyin.tech/literature_test/cpz1419-fig-0003-m.jpg)
Biochemical inhibitor potency is seldom assessed by direct observation of enzyme complex/adduct. Typically, enzyme inhibition is indirectly assessed in in vitro assays with a detectable read-out for product formation as a measure of (remaining) enzyme activity. Consequently, reversible enzyme inhibition may have reached the enzyme-inhibitor binding equilibrium (reaction completion), but not all enzyme is occupied (unless [I] >> Kiapp) so the remaining fraction of unbound enzyme continues to convert substrate into product (Fig. 3C, left). The reaction is no longer accurately reflected by Equation I (Fig. 3B), as product concentration at reaction initiation does not reflect the initial binding equilibrium, and product concentration does not reach a plateau after reaching the noncovalent equilibrium (reaction completion) for reversible inhibitors. Therefore, time-dependent product formation is fitted to exponential one-phase association Equation II (Fig. 3D) to obtain observed reaction rate k obs from initial to final product formation velocity. For irreversible inhibitors, the initial velocity vi reflects the (remaining) enzyme activity after rapid noncovalent association, and final velocity vs = 0 as this reflects full enzyme inactivation.
Typically, substrate competition assays are run at various inhibitor concentrations, and the concentration-dependent k obs is fitted to obtain kinetic parameters (Fig. 3E). In this work, equations and simulations are tailored to competitive binding of inhibitor and substrate (Holdgate et al., 2017; Rufer, 2021). Consequently, the observed reaction rate k obs (Fig. 3E) in the presence of competing substrate is slower, and apparent kinetic constants (marked with app) need to be corrected for substrate competition to reflect the kinetic inhibitor potency. Unless otherwise noted, nonlinearity in the uninhibited control k ctrl (k obs of [I] = 0) is assumed to be 0. The relation between k obs and inhibitor concentration holds important information on the inhibitor binding mechanism. A linear k obs increase with inhibitor concentration is a hallmark of a one-step binding mode, as reaction rates are only limited by experimental factors such as solubility. Plots of k obs against two-step inhibitor concentrations are hyperbolic, as the experimental covalent EI* association rate is limited by EI occupancy, which reaches its maximum (k inact or k 5) at saturating inhibitor concentration, as shown in Figure 3E: [I] > 10KI for 2-step IRREV or [I] > 10Ki for 2-step REV. An exception to this general observation is inhibitors with a two-step binding mode that will display a linear relationship (Strelow, 2017) when assessed at all non-saturating inhibitor concentrations (Fig. 3F) or all saturating inhibitor concentrations (Fig. 3G). These one-step binding behaviors can be distinguished from the Y-intercept (Y0 = k ctrl for [I] << Kiapp and Y0 > k ctrl for [I] >> Kiapp) along with the noncovalent inhibition of enzyme activity (vi = vctrl for [I] << Kiapp) and vi < vctrl for [I] >> Kiapp).
EXPERIMENTAL METHODS AND DATA ANALYSIS
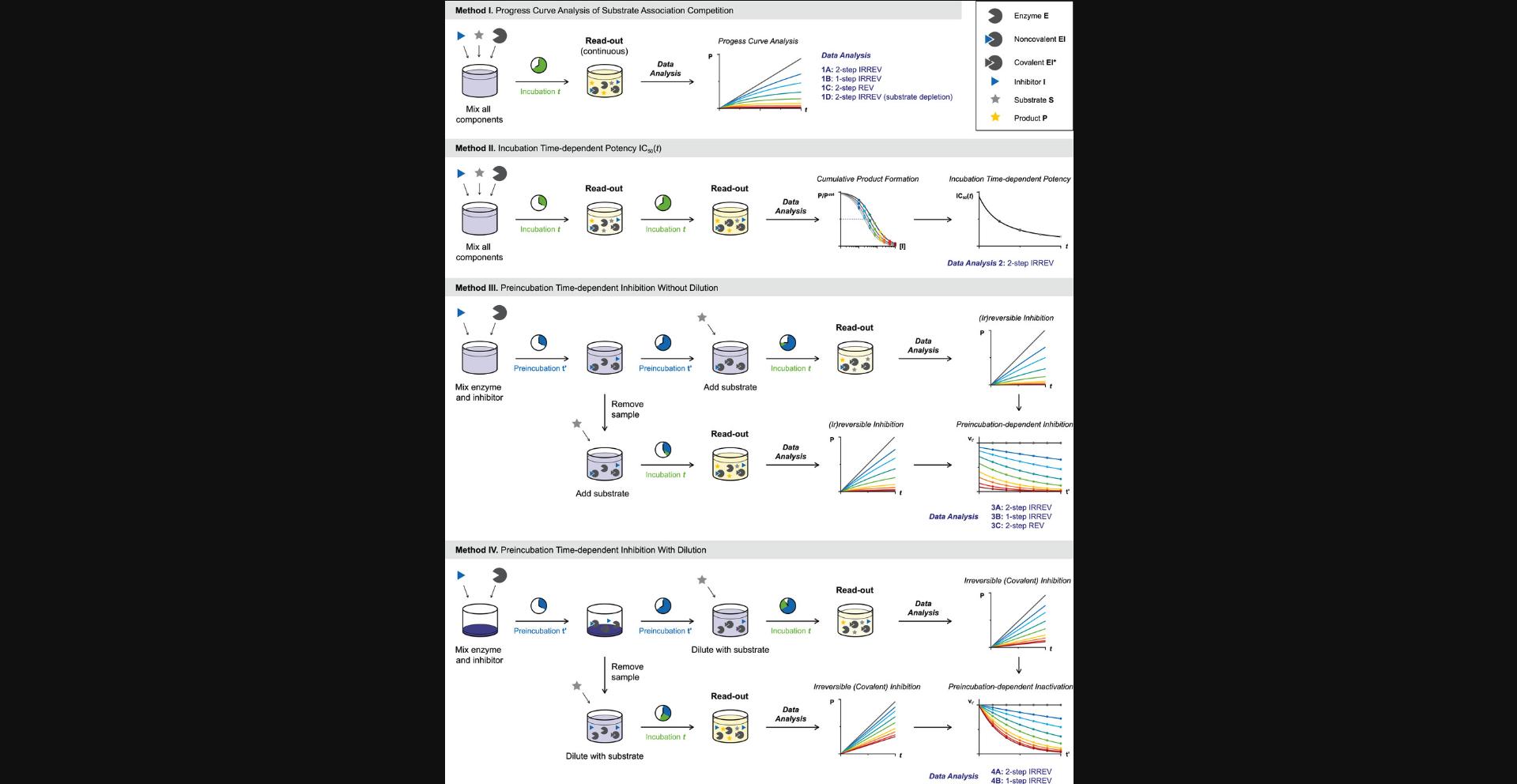
We will discuss four methods in this work (Progress Curve Analysis of Substrate Association Competition, Incubation Time–Dependent Potency IC50(t), Preincubation Time-Dependent Inhibition without Dilution, and Preincubation Time–Dependent Inhibition with Dilution/Competition) with accompanying data analysis protocols depending on the inhibitor binding mode (Fig. 4; also see Table 2). For each method, we will start with an overview of the general conceptual background and assay design considerations. Subsequent data analysis is subdivided into protocols tailored to a specific inhibitor binding mode, and for each data analysis protocol we will illustrate the ‘ideal’ situation with kinetic simulations to guide interpretation of results. A practical comment on the nomenclature used: we use the word ‘fit’ for nonlinear fits of raw data (in e.g., GraphPad as part of data analysis protocols) and ‘calculate’ to denote that we calculate parameters from experimental values (in e.g., EXCEL as part of sample calculations). Furthermore, pointers on identification of deviations such as nonlinearity in the uninhibited control (k ctrl > 0) will be given along with algebraic corrections or troubleshooting options to resolve issues.
| Method | Data analysis Protocol | Binding mode | Readout and experimental conditionsa | Obtainable kinetic parameters | Comments/remarks | Literature reference |
|---|---|---|---|---|---|---|
| I | 1A | 2-step IRREV | Continuous | kinact, KI & kinact/KI | Progress curve analysis is favored for very potent inhibitors as competing substrate is present during incubation. Optimization of reaction conditions to minimize assay artefacts can be challenging but rewards with the most simple experimental procedure. | Copeland, 2013b |
| 1B | 1-step IRREV | Continuous | kchem | |||
| 2-step IRREV | Continuous [I] << Kiapp | kinact/KI | ||||
| 1C | 2-step REV | Continuous kctrl << k6 | Ki* | Progress curve analysis is disfavored for 2-step reversible inhibitors as algebraic correction for spontaneous loss of enzyme activity is NOT possible. | ||
| 1D | 2-step IRREV | Continuous [P]t > 0.1[S]0 [S] << 0.1KM | kinact, KI & kinact/KI | Algebraic correction for substrate depletion. | Kuzmič et al., 2015 | |
| II | 2 | 2-step IRREV | Continuous/Quenched kctrl = 0 | kinact, KI & kinact/KI | Incubation time-dependent potency enables use of quenched assays but is sensitive to spontaneous loss of enzyme activity. | Krippendorff et al., 2009 |
| III | 3Ai | 2-step IRREV | Continuous/Quenched [S] << KM Vsub << Vt′ | kinact, KI & kinact/KI | Preincubation without dilution is favored for inhibitors with low potency as preincubation is performed in absence of competing substrate. Experimentally, assays are more time-consuming than Methods I & II. Data Analysis Protocols 3Ai and 3Bi are favored for comparison of multiple inhibitors on a single target. Data Analysis Protocols 3Aii and 3Bii are favored for selectivity evaluation of a single inhibitor on multiple targets. | Ito et al., 1998 |
| 3Aii | 2-step IRREV | Continuous/Quenched [S] << KM Vsub << Vt′ | kinact, KI & kinact/KI | |||
| 3Bi | 1-step IRREV | Continuous/Quenched [S] << KM Vsub << Vt′ | kchem | |||
| 2-step IRREV | Continuous/Quenched [S] << KM Vsub << Vt′ [I] << KI | kinact/KI | ||||
| 3Bii | 1-step IRREV | Continuous/Quenched [S] << KM Vsub << Vt′ | kchem or kobs/I | |||
| 2-step IRREV | Continuous/Quenched [S] << KM Vsub << Vt′ [I] << KI | kinact/KI | ||||
| 3C | 2-step REV | Continuous/Quenched [S] << KM Vsub << Vt′ | Ki* | Favored for 2-step REV inhibitors, with algebraic correction for spontaneous loss of enzyme activity by normalization. | ||
| IV | 4Ai | 2-step IRREV | Continuous/Quenched [S] >> KM Vsub >> Vt′ | kinact, KI & kinact/KI | Preincubation without dilution is favored for inhibitors with low (noncovalent) affinity, or to study the contribution of covalent bond formation. Data Analysis Protocols 4Ai and 4Bi are favored for comparison of multiple inhibitors on a single target. Data Analysis Protocols 4Aii and 4Bii are favored for selectivity evaluation of a single inhibitor on multiple targets. | Kitz & Wilson, 1962 |
| 4Aii | 2-step IRREV | Continuous/Quenched [S] >> KM Vsub >> Vt′ | kinact, KI & kinact/KI | |||
| 4Bi | 1-step IRREV | Continuous/Quenched [S] >> KM Vsub >> Vt′ | kchem | |||
| 2-step IRREV | Continuous/Quenched [S] >> KM Vsub >> Vt′ [I] << KI | kinact/KI | ||||
| 4Bii | 1-step IRREV | Continuous/Quenched [S] >> KM Vsub >> Vt′ | kchem or kobs/I | |||
| 2-step IRREV | Continuous/Quenched [S] >> KM Vsub >> Vt′ [I] << KI | kinact/KI or kobs/I | ||||
- a General assay conditions for all methods (unless otherwise noted/specified): [I] > 10[E]. [S] > 10[E]. [P]t < 0.1[S]0.
Methods I and II are based on incubation time–dependent enzyme inhibition (Fig. 4). Here, substrate and inhibitor are mixed, and the reaction is initiated by addition of enzyme: i.e., simultaneous onset of product formation and enzyme inhibitor. Methods III and IV are based on enzyme inhibition after preincubation. Here, enzyme is preincubated with inhibitor before substrate addition. Two major factors contribute to selection of the appropriate experimental method for your enzymatic inhibition assay: the available enzyme activity assay and the inhibitor binding mode. Recombinant enzyme inhibition is assessed in an in vitro enzyme activity assay with detectable product formation (Acker & Auld, 2014; Bisswanger, 2014). This can be a continuous read-out for enzymatic processing of fluorogenic substrates (e.g., fluorescence intensity, FRET) or be a stopped/quenched assay that may require a secondary development/quenching or separation step to detect the formed product (or remaining substrate) such as LC/MS-based assays, conversion of radiolabeled substrate, and commercial assay technologies including ADP-GloTM (Promega) ATP consumption/ADP production assays, HTRF® KinEASETM (Cisbio) and Z′-LYTE (Invitrogen) phosphorylation assays, and Amplex® Red (Invitrogen) hydrogen peroxide/peroxidase assays (Acker & Auld, 2014; Bisswanger, 2014). Method I is only compatible with homogeneous enzymatic assays that allow continuous read-out, such as cleavage of fluorogenic reporter peptides by proteases. Methods II-IV are also compatible with quenched/stopped assays with development step prior to read-out.
METHOD I: PROGRESS CURVE ANALYSIS OF SUBSTRATE ASSOCIATION COMPETITION
Progress curve analysis is an established method for kinetic analysis of slow-binding inhibitors based on continuous detection of product formation after the substrate processing/product formation reaction has been initiated by addition of enzyme to a mixture of inhibitor and substrate (Fig. 5A). A single measurement at each inhibitor concentration is sufficient, which is convenient when comparing the potency of multiple inhibitors on the same target. However, this method requires the availability of an activity assay format with a continuous read-out, thereby limiting the substrates that can be used. Additionally, assay optimization for progress curve analysis is labor intensive: it is not uncommon to perform multiple pilot experiments to find suitable concentrations of substrate, enzyme, and inhibitor that ensure linear product formation in the uninhibited control (consult Table 3 in the troubleshooting section near the end of the article for troubleshooting).
![Details are in the caption following the image Method I: Progress curve analysis of substrate association competition. Simulated with KinGen for 1 pM enzyme and 100 nM substrate S1. (A) The reaction between enzyme, inhibitor, and substrate is initiated by addition of enzyme. Product formation is monitored continuously to detect the time-dependent enzyme activity. Top: simulated for 50 nM reversible two-step inhibitor B. Bottom: simulated for 50 nM irreversible two-step inhibitor C. Enzyme inhibition increases with time-dependent formation of covalent EI* until reaching reaction completion. Initially, total enzyme occupancy [EI + EI*] reflects the rapid noncovalent equilibrium [EI]<sub>eq</sub>. At reaction completion (t > 5t½), total enzyme occupancy EI + EI* reflects the steady-state equilibrium (reversible) or inactivation (irreversible). (B) Typical progress curves for enzyme activity in presence of time-dependent inhibitors. Time-dependent product formation decreases exponentially from initial velocity v<sub>i</sub> (dashed green line) to the steady-state velocity v<sub>s</sub> (dashed purple line) at reaction completion (t > 5t½). v<sub>i</sub> = v<sup>ctrl</sup> when [I] << K<sub>i</sub><sup>app</sup> (and for one-step inhibitors) with v<sup>ctrl</sup> = linear product formation in uninhibited control (gray line). Simulated for 50 nM one-step reversible inhibitor A, two-step reversible inhibitor B, one-step irreversible inhibitor D, or two-step irreversible inhibitor C. (C) General exponential association Equation II to fit progress curves of time-dependent inhibition. Parameters are constrained depending on the inhibitor binding mode. Irreversible inhibition: v<sub>s</sub> = 0 (inactivation at reaction completion). One-step inhibition: v<sub>i</sub> = v<sup>ctrl</sup> (noncovalent complex is not significant at non-saturating inhibitor concentrations). F<sub>t</sub> = time-dependent signal resulting from product formation (in AU). F<sub>0</sub> = Y-intercept = background signal at reaction initiation (in AU). v<sub>i</sub> = initial product formation velocity (in AU/s). v<sub>s</sub> = final/steady-state product formation velocity (in AU/s). t = incubation time after enzyme addition (in s). k<sub>obs</sub> = observed rate of time-dependent inhibition from initial v<sub>i</sub> to final v<sub>s</sub> (in s<sup>−1</sup>). Also fit the uninhibited/fully inhibited controls to obtain reference values for uninhibited velocity v<sup>ctrl</sup> and the rate of nonlinearity in the uninhibited control k<sub>ctrl</sub>.](https://static.yanyin.tech/literature_test/cpz1419-fig-0005-m.jpg)
For ‘slow-binding’ inhibitors, the slope of time-dependent product formation exponentially decreases from initial product formation velocity vi (rapid noncovalent inhibition) to the final product formation velocity vs (reaction completion) (Fig. 5B) (Copeland, 2013b). The progress curve of time-dependent product formation (as detected signal F t in AU) is fitted to a general exponential inhibitor association Equation II (Fig. 5C) to obtain the observed rate of reaction completion k obs (in s−1) from initial velocity vi (in AU/s) to final velocity vs (in AU/s). One-step or two-step binding modes can be identified by (visual) inspection of the initial velocity (Fig. 5B). The value of initial velocity vi is inhibitor concentration–dependent for two-step (ir)reversible inhibitors that form a rapid (noncovalent) equilibrium (vi < vctrl) because the noncovalent enzyme-inhibitor complex already inhibits the enzyme activity (rapid equilibrium approximation). Similarly, the value of initial velocity vi is equal to the uninhibited velocity vctrl in lieu of a rapid initial binding step, as can be observed for two-step (ir)reversible inhibitors at non-saturating concentrations ([I] << Kiapp) and one-step (ir)reversible inhibitors (vi < vctrl). Irreversible inhibitors are expected to reach 100% inhibition at reaction completion for all inhibitor concentrations, provided inhibitor is present in large excess and the reaction does not exceed the dynamic enzyme lifetime. Therefore, the final velocity vs is restrained to full inhibition (vs = 0) for two-step irreversible inhibitors (Data Analysis 1A) and one-step irreversible inhibitors (Data Analysis 1B). Two-step reversible inhibitors will reach a reversible steady-state equilibrium (vs ≥ 0) upon reaction completion (Data Analysis 1C). Be aware that the product formation progress curve is not only linear for fast-binding inhibitors but will also appear linear for slow-binding inhibitors if reaction completion is much slower than the time course of the assay (t << t½). Importantly, the noncovalent equilibrium is assumed to be reached instantly for two-step inhibitors (rapid equilibrium approximation). An algebraic solution to analyze irreversible two-step inhibitors violating the rapid equilibrium approximation is available as a preprint (Kuzmič, 2020a).
It is crucial to have linear product formation in the uninhibited control (F ctrl), as progress curve fitting for time-dependent (ir)reversible inhibition relies on the assumption that uninhibited product formation is absolutely linear. This ideal situation is often not feasible to achieve experimentally, as there are many factors contributing to a slight time-dependent decrease of product formation velocity in the uninhibited control, and not all of them are resolvable (common troubleshooting options are listed in Table 3 in the troubleshooting section near the end of the article). It is possible to correct algebraically. Algebraic correction for nonlinearity in the uninhibited control k ctrl caused by spontaneous enzyme degradation/denaturation is possible for irreversible inhibitors (Data Analysis 1A-B). Furthermore, it is also possible to perform an algebraic correction for substrate depletion for two-step irreversible inhibitors (Data Analysis 1D) (Kuzmič, Solowiej, & Murray, 2015). Ultimately, numerical integration is the preferred method in complex systems where multiple events contribute to the observed nonlinearity.
Basic Protocol 1: Progress Curve Analysis of Substrate Association Competition
The protocol below provides a generic set of steps to accomplishing this type of measurement. A practical example with specific reagents, and assay conditions for progress curve analysis of covalent Cathepsin K inhibitors can be found in Mons et al. (2019).
Materials
- 1× Assay/reaction buffer supplemented with co-factors and reducing agent
- Active enzyme, 4× solution in assay buffer
- Substrate with continuous read-out, 4× solution in assay buffer
- Positive control: vehicle/solvent as DMSO stock, or 2% solution in assay buffer
- Negative control: known inhibitor or alkylating agent as DMSO stock, or 2× solution in assay buffer
- Inhibitor: as DMSO stock, or serial dilution of 2× solution in assay buffer with 2% DMSO
- 384-well low volume microplate with nonbinding surface (e.g., Corning 3820 or 4513) for incubation and read-out
- Optical clear cover/seal (e.g., Perkin Elmer TopSeal-A Plus, #6050185, Corning 6575 Universal Optical Sealing Tape or Duck Brand HP260 Packing Tape)
- 1.5 ml (Eppendorf) microtubes to prepare stock solutions
- Optional : 96-well microplate to prepare serial dilution of inhibitor concentration
- Microplate reader equipped with appropriate filters to detect product formation (e.g., CLARIOstar microplate reader)
- Optional : Automated (acoustic) dispenser (e.g., Labcyte ECHO 550 Liquid Handler acoustic dispenser)
Before you start , optimize assay conditions in the uninhibited control to ensure compliance with assumptions and restrictions for progress curve analysis—most importantly linear product formation in the uninhibited control for the duration of the experiment (k ctrl = 0) — by activating the enzyme before reaction initiation (e.g., preincubation with reducing agent for proteases, or ATP for kinases and ligases), testing the enzyme activity on the (fluorogenic) substrate in absence of inhibitor, and adjusting the enzyme and substrate concentration ([S] 0>10[E]0) to reach maximum 10% substrate conversion at the end of the measurement window ([P]t < 0.1[S]0). Further optimization typically involves tuning the reader settings for optimal sensitivity, measurement of a calibration curve for product concentration (Dharadhar et al., 2019; Janssen et al., 2019), and calculation of the Z′-score from the uninhibited and inhibited controls (ideally 8 replicates) in a separate experiment (Zhang, Chung, & Oldenburg, 1999) to validate that enough product is formed for a good signal/noise ratio (Z′ > 0.5) at the end of the measurement. Consult Table 3 in the troubleshooting section near the end of the article for common optimization and troubleshooting options. The read-out of product formation must be homogeneous/continuous. Product formation of substrates with a less sensitive read-out (e.g., fluorescence polarization) may generate a relatively low product signal relative to the unprocessed substrate, and substrate depletion is unavoidable to generate a sufficient Z′-score (Zhang et al., 1999). Algebraic analysis of two-step irreversible inhibition with substrate depletion ([P]t < 0.1[S]0) can be performed with Data Analysis Protocol 1D after completion of Basic Protocol I , steps 2-6.
1.Add inhibitor or control to each well with the uninhibited control for full enzyme activity containing the same volume vehicle/solvent instead of inhibitor (we use DMSO in this protocol). Add a constant volume of serially diluted inhibitor in assay buffer supplemented with DMSO (e.g., 10.2 µl of 2× solution containing 2% DMSO), or add inhibitor and controls by (acoustic) dispensing of the pure DMSO stocks, with DMSO backfill to a constant volume (e.g., 0.2 µl), followed by addition of assay buffer to each well (e.g., 10 µl) and gentle shaking (300 rpm) to homogenize the solution.
Typically, measurements are performed in triplicate (or more replicates) with at least 8 inhibitor concentrations. Inhibitor concentrations might need optimization, but a good starting point is 0.1-10×IC50; the highest inhibitor concentration should correspond to maximum 90% initial (noncovalent) inhibition (vi > 0.1vctrl), as it can be difficult to accurately detect the increase from 90% to 100% inhibition.
2.Add substrate in assay buffer to each well (e.g., 5 µl of 4× solution) and homogenize the solutions by gentle shaking (300 rpm).
The order of substrate or inhibitor addition is not important per se , as long as enzyme is the last reagent to be added, and DMSO stocks are added prior to buffered (aqueous) solutions. Optionally, gently centrifuge the plate (1 min at 1000 rpm) to ensure that assay components are not stuck at the top of the well.
3.Add active enzyme in assay buffer to each well (e.g., 5 µl of 4× solution), with minimal delay between addition to the first and the last well. Optionally, gently centrifuge the plate (1 min at 1000 rpm) if bubbles are formed (especially for buffers containing surfactants), as these will induce assay artifacts, and to ensure assay components are in solution together rather than stuck to the wall at the top of the well.
Manual addition of enzyme solution and physically moving the plate to the plate reader introduces a delay that may slightly affect the accuracy of the measurement, as it can be variable (depending on the total number of wells, distance to the machine and walking pace of the researcher). This should not be significant if the delay is short compared to the total reaction time, but it can affect the outcome in the data analysis when t0 is actually 1-2 min. One method to monitor the delay between reaction initiation (onset of product formation and inhibition) and the start of product detection in step 6 is evaluation of the Y-intercept values (as discussed in Table 3). Alternatively, enzyme addition with an injector built into the plate reader minimizes the delay between reaction initiation (onset of product formation and inhibition) and starting the measurement.
4.Seal the wells by applying an optical clear cover.
Continuous kinetic measurements are subject to assay artifacts such as drift due to evaporation. In our experience, application of an optical clear cover/seal prior to measurement improves the assay robustness and resolves significant aberrant nonlinearity unrelated to enzyme activity.
5.Measure product formation in microplate reader by detection of the product read-out.
A typical assay measurement window is 60-240 min, with a measurement interval of 1-2 min. The inhibitor-binding reaction does not have to reach completion (100% inhibition for irreversible inhibitors, equilibrium for reversible inhibitors) within this window, but data will be more reliable when completion is reached before the end of the measurement (Fig. 5B).
6.Proceed to Basic Data Analysis Protocols to calculate the appropriate kinetic parameters for each covalent binding mode: Data Analysis Protocol 1A for two-step irreversible inhibitors, Data Analysis Protocol 1B for one-step irreversible inhibitors, Data Analysis Protocol 1C for two-step reversible inhibitors, or Data Analysis Protocol 1D for two-step irreversible inhibitors with substrate depletion.
| Data Analysis Protocol | |||
|---|---|---|---|
| EXP Conditions | 2-step IRREV | 1-step IRREV | 2-step REV |
| kctrl = 0 | 1A | 1B | 1C |
| kdegE > 0 | 1A | 1B | – |
| [P]t > 0.1[S]0 | 1D | – | – |
Exemplary assay concentrations.
| Concentration during incubation t | |||
|---|---|---|---|
| [stock] | V (µl) | [conc]t | |
| Enzyme | 4 nM | 5 | 0.99 nM |
| Inhibitor | 20 nM | 10.2 | 10.10 nM |
| Substrate | 4 µM | 5 | 0.99 µM |
| Total | 20.2 | ||
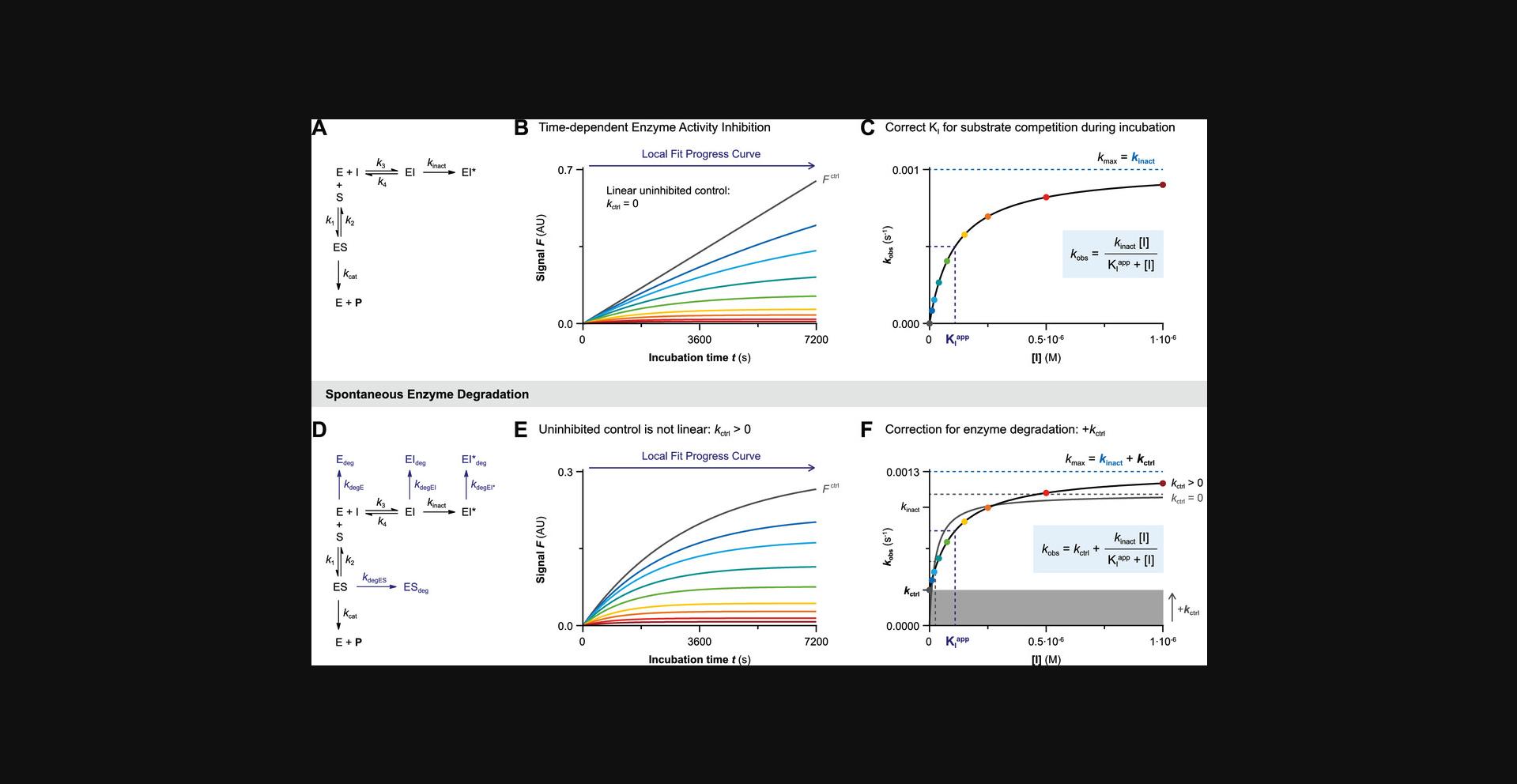
Data Analysis 1A: Progress Curve Analysis for Two-Step Irreversible Covalent Inhibition
The progress curve of time-dependent product formation of each inhibitor concentration is fitted to exponential Equation II (Fig. 5C) constraining final velocity to 100% inhibition (vs = 0) at reaction completion (Fig. 6A and 6B). The inhibitor concentration–dependent observed rate of inactivation k obs reflects the rate from initial velocity vi (rapid noncovalent equilibrium) to final velocity vs (inactivation at reaction completion). The plot of inhibitor concentration–dependent k obs reaches maximum rate of inactivation k inact in the presence of saturating inhibitor concentration ([I] >> KIapp) with the Y-intercept at 0 when the progress curve in absence of inhibitor is strictly linear (Fig. 6C). Importantly, the inhibitor concentration that results in half-maximum enzyme inactivation (k obs = ½× k inact) has to be corrected for competition by the substrate during incubation but maximum rate of inactivation k inact is unaffected.
Warnings and remarks
A linear plot of inhibitor concentration-dependent k obs (with Y-intercept = k ctrl) and an initial velocity independent of inhibitor concentration (vi = vctrl) are indicative of a one-step binding mechanism: the inhibitor concentration is not saturating ([I] ≤ 0.1KIapp and [I] ≤ 0.1Kiapp). This can be resolved by increasing the inhibitor concentration, reducing the substrate concentration, or processing the data with Basic Data Analysis Protocol 1B. Inhibitors with a high noncovalent potency ([I] >> Kiapp) might exhibit tight-binding behavior: complete inactivation is reached at reaction initiation (vi = 0), even at the lowest inhibitor concentration, without violating the pseudo-first order reaction conditions ([I]0 ≥ 10[E]0). This can be resolved by lowering the inhibitor concentration, but only if the assay robustness is sufficient to also lower the enzyme concentration, and/or by increasing the concentration of competing substrate, thus increasing the apparent inhibition constant Kiapp. Unfortunately, algebraic correction for progress curve analysis of one-step inhibitors (Copeland, 2013b) with inhibitor depletion ([I]0 < 10[E]0) is not compatible with two-step inhibition. Numeric fitting is a possibility to fit progress curves with depletion of substrate as well as inhibitor (Kuzmič, 2015). Alternatively, tight-binding two-step irreversible covalent inhibition can be assessed with Method IV if covalent adduct formation is relatively slow.
Spontaneous enzyme degradation/denaturation causes a nonlinearity in the uninhibited control (k ctrl > 0) that violates the assumption that time-dependence in the inhibitor-treated samples is a direct effect of the inhibitor (Fig. 6D and 6E). The first-order enzymatic degradation rate contributes to k obs independent of inhibitor concentration (k degE = k degES = k degEI). Consequently, the Y-intercept of the k obs against inhibitor concentration plot now corresponds to observed rate k ctrl in absence of inhibitor, and k max is higher (k max = k inact + k ctrl) (Fig. 6F). Performing a simple algebraic correction for the observed nonlinearity due to spontaneous enzyme degradation results in good estimates for k inact and KIapp (Fig. 6F). Ignoring the nonlinearity in the uninhibited control by restraining k ctrl = 0 implies that all time-dependent loss of enzyme activity should be attributed to inhibitor-mediated inactivation, resulting in an underestimation of inactivation constant KIapp (overestimation of potency) and overestimation of k inact. This effect is less pronounced when spontaneous enzyme degradation is much slower than the maximum rate of covalent adduct formation (k inact >> k ctrl). It is important to note that stabilization of the enzyme species by (noncovalent) inhibitor binding also decreases the contribution of k ctrl to the observed rate k obs at saturating inhibitor concentrations (k max = k inact). This impairs the accuracy of the algebraic correction unless k ctrl is relatively small (k max approaches k inact if k inact >> k ctrl).
This algebraic correction does not accurately correct for nonlinearity due to substrate depletion ([P]t > 0.1[S]0): substrate depletion is dependent on the total product formation and does not (significantly) contribute to k max at saturating inhibitor concentration because enzyme inhibition reduces the total amount of product formed (k max = k inact). Please consult Data Analysis 1D for algebraic correction of nonlinearity due to substrate depletion.
Basic Protocol 2: Two-Step Irreversible Covalent Inhibition
Processing of raw data obtained with Basic Protocol I for two-step irreversible covalent inhibitors.
1.Plot signal F against incubation time t.
Plot signal (in AU) on the Y-axis against incubation time (in s) on the X-axis for each inhibitor concentration and the controls (Fig. 6B). Product formation in the uninhibited control F ctrl should be linear. Consult Table 3 for troubleshooting of nonlinearity of the uninhibited control. Optionally, perform background correction to correct for assay artifacts such as bleaching and drift that cause a negative final velocity (vs < 0 AU/s) in the fully inhibited control. This correction can be subtraction of the background in presence of substrate (and inhibitor) but absence of enzyme, or subtraction of the fully inhibited control.
2.Fit signal F t against t to obtain k obs
Fit signal F t against incubation time t to Equation II (Fig. 6B/E). Constrain final velocity vs = 0 (in AU/s) for background-corrected product formation, or vs = value for full inhibition control. A lack of initial noncovalent complex (vi = vctrl) is indicative of one-step binding behavior.
\begin{equation} {F_{\rm {t}}} = ;{{\rm{v}}{\rm{s}}}t + \frac{{{{\rm{v}}{\rm{i}}} - {{\rm{v}}{\rm{s}}}}}{{{k{{\rm{obs}}}}}}\left[ {1 - {e^{ - {k_{{\rm{obs}}}}t}}} \right] + {F_0} \end{equation}
Equation II for nonlinear regression of user-defined explicit equation Y = (vsX) + (((vi-vs)/kobs)(1-EXP(-kobs*X))) + Y0 with Y = signal F t (in AU) and X = incubation time t (in s) to find Y0 = Y-intercept F 0 = background signal at t = 0 (in AU), vi = initial slope vi (in AU/s), vs = final slope vs (in AU/s) and kobs = observed reaction rate k obs (in s−1).
3.Plot k obs against [I].
Plot the mean and standard deviation of k obs (in s−1) on the Y-axis against inhibitor concentration (in M) after reaction initiation by enzyme addition (in the final solution) on the X-axis (Fig. 6C/F). The plot of k obs against [I] should reach a maximum k obs at saturating inhibitor concentration. Note that a linear curve is indicative of one-step binding behavior at non-saturating inhibitor concentrations ([I] << 0.1KIapp in Fig. 3F) with vi = vctrl (low initial inhibition). Proceed to Basic Data Analysis Protocol 1B , step 4, after it has been validated that the linear curve is not resultant from saturating inhibitor concentrations ([I] >> 10KIapp in Fig. 3G) as identified by vi << vctrl (significant initial inhibition), by repeating the measurement with a higher competitive substrate concentration (increase KIapp) and/or lower inhibitor concentration.
4.Fit k obs against [I] to obtain k inact and KIapp.
Fit k obs against inhibitor concentration to Equation VII to obtain maximum inactivation rate constant k inact (in s−1) and apparent inactivation constant KIapp (in M). Constrain k ctrl = k obs of the uninhibited control (Fig. 6F). Calculate inactivation constant KI (in M) and irreversible covalent inhibitor potency k inact/KI (in M−1s−1) with Sample Calculation 1 &2.
\begin{equation} {k_{{\rm{obs}}}} = {k_{{\rm{ctrl}}}} + \frac{{{k_{{\rm{inact}}}}\left[ {\rm{I}} \right]}}{{{{\rm{K}}_{\rm{I}}}^{{\rm{app}}} + \left[ {\rm{I}} \right]}} \end{equation}
Equation VII for nonlinear regression of user-defined explicit equation Y = Y0 + ((kmax*X)/((KIapp) + X)) with Y = observed reaction rate k obs (in s−1) and X = inhibitor concentration (in M) to find Y0 = rate of nonlinearity in uninhibited control k ctrl (in s−1), kmax = maximum reaction rate k inact (in s−1) and KIapp = Apparent inactivation constant KIapp (in M).
5.EXTRA: Plot and fit vi against [I] to obtain Kiapp.
Inhibition constant Ki can be calculated from the initial velocity vi (obtained in step 3), reflecting the rapid (initial) noncovalent enzyme-inhibitor equilibrium. Plot the mean and standard deviation of vi (in AU/s) on the Y-axis against inhibitor concentration on the X-axis (similar to Fig. 8D). Fit vi against [I] to four-parameter nonlinear regression Hill Equation VIII (Copeland, 2013e) to obtain apparent inhibition constant Kiapp (in M). Constrain the top to the uninhibited vi (maximum velocity = vctrl) and the bottom to the fully inhibited vi (vimin = minimum velocity. For (background-)corrected product formation vimin = 0). Calculate inhibition constant Ki (in M) with Sample Calculation 3.
\begin{equation} {{\rm{v}}{\rm{i}}} = {\rm{v}}{\rm{i}}^{{\rm{min}}} + \frac{{{{\rm{v}}^{{\rm{ctrl}}}} - {\rm{v}}{\rm{i}}^{{\rm{min}}}}}{{1 + {{\left( {\frac{{\left[ {\rm{I}} \right]}}{{{{\rm{K}}{\rm{i}}}^{{\rm{app}}}}}} \right)}^h}}} \end{equation}
Equation VIII for nonlinear regression of four-parameter dose-response equation Y = Bottom + (Top-Bottom)/(1 + (X/IC50)^HillSlope) with Y = initial product formation velocity vi (in AU/s), X = inhibitor concentration (in M), Bottom = velocity in fully inhibited control vimin (in AU/s), and Top = maximum velocity in uninhibited control vctrl (in AU/s) to find Hillslope = Hill coefficient h (unitless) and IC50 = apparent inhibition constant Kiapp (in M).
6.Optional : Validate experimental kinetic parameters with kinetic simulations.
Proceed to Kinetic Simulations 1 to compare the experimental progress curves to the progress curves simulated with scripts KinGen and KinDeg (using experimental rate constant k inact = k 5) to confirm that the calculated kinetic constants are in accordance with the experimental data.
Data Analysis 1B: Progress Curve Analysis for One-Step Irreversible Covalent Inhibition
The progress curve of time-dependent product formation of each inhibitor concentration is fitted to exponential Equation II (Fig. 5C) constraining final velocity to inactivation (vs = 0) at reaction completion (Fig. 7A and 7B). The initial velocity vi equals the uninhibited product formation velocity (vi = vctrl), as noncovalent inhibitor binding does not contribute to enzyme inhibition by one-step irreversible inhibitors. A linear plot of inhibitor concentration–dependent k obs is indicative of a one-step binding mechanism with k chemapp as the slope (Fig. 7C). Two-step irreversible covalent inhibitors also have a linear k obs against inhibitor concentration plot at non-saturating concentrations ([I] ≤ 0.1KIapp) with k chemapp = k inact/KIapp.
![Details are in the caption following the image Data Analysis 1B: Progress curve analysis for one-step irreversible covalent inhibition. Simulated with KinGen (A-C) or KinDeg (D-F) for inhibitor D with 1 pM enzyme and 100 nM substrate S1. (A) Schematic enzyme dynamics during incubation for one-step irreversible covalent inhibition. (B) Time-dependent product formation in absence of inhibitor F<sup>ctrl</sup> or in presence of inhibitor. The progress curve for each inhibitor concentration is fitted individually to Equation II (Fig. 5C) (constraining v<sub>s</sub> = 0) to obtain the observed rate of inactivation k<sub>obs</sub>. v<sub>i</sub> = v<sup>ctrl</sup> for one-step irreversible inhibitors and two-step irreversible inhibitors at non-saturating concentrations ([I] << K<sub>i</sub><sup>app</sup>). (C) Inhibitor concentration–dependent k<sub>obs</sub> increases linearly with inhibitor concentration, with k<sub>chem</sub><sup>app</sup> as the slope. (D) Schematic enzyme dynamics during incubation for one-step irreversible covalent inhibition with spontaneous loss of enzyme activity. Simulated with k<sub>degE</sub> = k<sub>degES</sub> = k<sub>degEI</sub> = 0.0003 s<sup>−1</sup>. (E) Time-dependent product formation in absence of inhibitor F<sup>ctrl</sup> is not linear because k<sub>ctrl</sub> > 0. The progress curves for each inhibitor concentration and uninhibited control are fitted individually to Equation II (Fig. 5C) (constraining v<sub>s</sub> = 0) to obtain the observed rates of inactivation k<sub>obs</sub>. (F) Inhibitor concentration–dependent k<sub>obs</sub> with spontaneous enzyme degradation/denaturation increases by k<sub>ctrl</sub>. Fit with algebraic correction for nonlinearity (black line, k<sub>ctrl</sub> > 0) or ignoring nonlinearity (gray line, constrain k<sub>ctrl</sub> = 0). Ignoring the nonlinearity (assuming Y-intercept = 0) results in overestimation of k<sub>chem</sub><sup>app</sup> (steeper slope).](https://static.yanyin.tech/literature_test/cpz1419-fig-0007-m.jpg)
Warnings and remarks
The slope has to be corrected for substrate competition to obtain the inactivation constant k chem (in M−1s−1). Substrate will occupy a fraction of the unbound enzyme to reach the noncovalent E + S <-> ES equilibrium (how much depends on [S]/KM), thus reducing the unbound enzyme concentration. It may seem counterintuitive to correct for substrate competition, as the pseudo-first-order rate of covalent adduct formation (k obs = k chemapp[I]) does not seem to involve unbound enzyme (provided inhibitor is present in large excess), but formation of EI* is limited by the available unbound enzyme at that moment and it is not possible to form covalent adduct EI* when competing substrate blocks access to the enzyme active site.
It is important to have linear product formation in the uninhibited control (k ctrl = 0) or to perform an algebraic correction for nonlinearity in the uninhibited control (k ctrl > 0) caused by spontaneous first-order enzyme degradation/denaturation (Fig. 7D-F). Failure to correct for the contribution of enzyme degradation when fitting the observed rate of inactivation k obs against inhibitor results in overestimation of k chemapp (Fig. 7F, gray line). The contribution of nonlinearity k ctrl becomes less pronounced at elevated inhibitor concentrations as k ctrl becomes significantly smaller than k obs (k ctrl << k chemapp[I]). (De)stabilization of enzyme upon inhibitor binding (k degEI*) does not affect k obs, as EI* formation is already irreversible, thus removing the species from the available pool of catalytic enzyme. To our knowledge, methods to algebraically correct for substrate depletion have not been reported.
Basic Protocol 3: One-Step Irreversible Covalent Inhibition
Processing of raw data obtained with Basic Protocol I for one-step irreversible covalent inhibitors and two-step irreversible inhibitors at non-saturating inhibitor concentrations ([I] ≤ 0.1Kiapp).
1.Plot signal F against incubation time t.
Plot signal (in AU) on the Y-axis against incubation time (in s) on the X-axis for each inhibitor concentration and the controls (Fig. 7B). Product formation in the uninhibited control F ctrl should be linear. Consult Table 3 for troubleshooting of nonlinearity of the uninhibited control. Optionally, perform background correction to correct for assay artifacts such as bleaching and drift that cause a negative final velocity (vs < 0 AU/s) in the fully inhibited control. This correction can be subtraction of the background in presence of substrate (and inhibitor) but absence of enzyme, or subtraction of the fully inhibited control.
2.Fit F t against t to obtain k obs.
Fit signal F t against incubation time t to Equation II (Fig. 7B/E). Constrain final velocity vs = 0 (in AU/s) for background-corrected product formation, or vs = value for full inhibition control. Initial velocity vi should be a shared value because noncovalent inhibition does not significantly contribute to the initial inhibition for inhibitors displaying one-step behavior.
\begin{equation} {F_{\rm {t}}} = ;{{\rm{v}}{\rm{s}}}t + \frac{{{{\rm{v}}{\rm{i}}} - {{\rm{v}}{\rm{s}}}}}{{{k{{\rm{obs}}}}}}\left[ {1 - {e^{ - {k_{{\rm{obs}}}}t}}} \right] + {F_0} \end{equation}
Equation II for nonlinear regression of user-defined explicit equation Y = (vsX) + (((vi-vs)/kobs)(1-EXP(-kobs*X))) + Y0 with Y = signal F t (in AU) and X = incubation time t (in s) to find Y0 = Y-intercept F 0 = background signal at t = 0 (in AU), vi = initial slope (in AU/s), vs = final slope (in AU/s) and k obs = observed reaction rate k obs (in s−1).
3.Plot k obs against [I].
Plot the mean and standard deviation of k obs (in s−1) on the Y-axis against inhibitor concentration (in M) after reaction initiation by enzyme addition (in the final solution) on the X-axis (Fig. 7B/E). The plot of k obs against inhibitor concentration [I] is linear for one-step irreversible inhibitors and for two-step irreversible inhibitors at non-saturating inhibitor concentrations ([I] << 0.1Kiapp).
4.Fit k obs against [I] to obtain k chemapp.
Fit k obs against inhibitor concentration to Equation IX to obtain apparent inhibitor potency k chemapp (in M−1s−1) from the linear slope. Constrain Y-intercept k ctrl = k obs of the uninhibited control (Fig. 7F). Calculate k chem (in M−1s−1) reflecting inhibitor potency for one-step irreversible covalent inhibition with Sample Calculation 4. Calculate k inact/KIapp (in M−1s−1) and k inact/KI (in M−1s−1) for two-step irreversible inhibitors at non-saturating inhibitor concentrations ([I] ≤ 0.1Kiapp) with Sample Calculation 5 and 6.
\begin{equation} {k_{{\rm{obs}}}} = {k_{{\rm{ctrl}}}} + k_{{\rm{chem}}}^{{\rm{app}}}\left[ {\rm{I}} \right] \end{equation}
Equation IX for nonlinear regression of straight line Y = YIntercept + Slope*X with Y = observed reaction rate k obs (in s−1) and X = inhibitor concentration (in M) to find YIntercept = rate of nonlinearity in uninhibited control k ctrl (in s−1) and Slope = apparent inactivation rate constant k chemapp (in M−1s−1).
5.Optional : Validate experimental kinetic parameters with kinetic simulations.
Proceed to Kinetic Simulations 1 to compare the experimental progress curves to the progress curves simulated with scripts KinGen and KinDeg (using experimental rate constant k chem = k 3) to confirm that the calculated kinetic constants are in accordance with the experimental data.
Data Analysis 1C: Progress Curve Analysis for Two-Step Reversible Covalent Inhibition
The progress curve of time-dependent product formation of each inhibitor concentration (Fig. 8A and 8B) is fitted to exponential Equation II (Fig. 5C). The inhibitor concentration-dependent observed rate for reaction completion k obs reflects the rate from initial velocity vi (rapid noncovalent equilibrium) to final velocity vs (slow steady-state equilibrium). Contrary to irreversible inhibition, steady-state velocity vs is not constrained to inactivation (vs > 0) because the reversible steady-state equilibrium is reached at reaction completion. Maximum rate of reaction completion k max is reached in the presence of saturating inhibitor concentration ([I] >> Kiapp), and the covalent association rate constant k 5 is obtained from the span between k min and k max. Interestingly, the Y-intercept k min is equal to covalent dissociation rate constant k 6; therefore, the k obs of uninhibited control (k ctrl) is excluded from the fit (Fig. 8C). Steady-state inhibition constant Kiapp can be calculated from the fitted values of Kiapp, k 5, and k 6, but this is not the preferred approach, as a small error in k 6 has huge implications for the calculation of Ki. Other methods such as jump dilution assays generate more reliable estimates of k 6, which is especially important for very potent two-step reversible covalent inhibitors: relatively small k 6-values cannot accurately be estimated from the Y-intercept (Copeland, 2013e; Copeland et al., 2011). Generally, more reliable estimates of the apparent steady-state inhibition constant Ki*app are generated from the dose-response curve of steady-state velocity vs against inhibitor concentration (Fig. 8D).
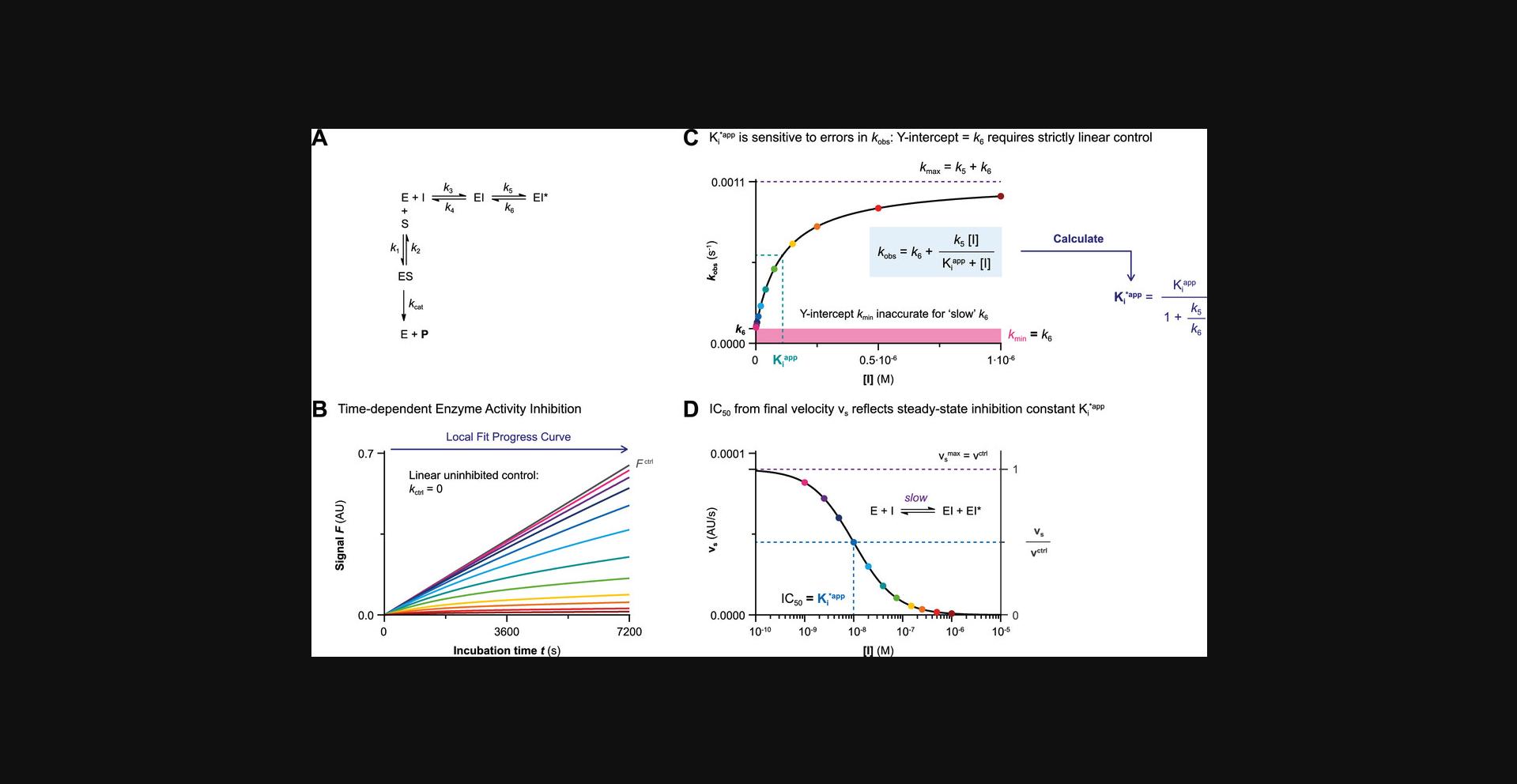
Warnings and remarks
It is crucial to have strictly linear product formation in the uninhibited control (k ctrl = 0) because it is not possible to perform an algebraic correction for spontaneous enzyme degradation/denaturation (Fig. 9A). Unfortunately, potent reversible covalent inhibitors are likely to violate this condition. Contrary to irreversible covalent inhibitors that become more potent with a faster k inact, reversible covalent inhibitors are more potent if they have a longer residence time τ, which is driven by a slow dissociation rate k 6 (Fig. 1B) (Copeland, 2010; Copeland et al., 2006). Violation of this assumption (k ctrl > 0) can be identified by fitting the uninhibited product formation F ctrl to Equation II (Fig. 5C): initial velocity victrl should not be larger than steady-state vsctrl. The consequence of nonlinearity in the uninhibited control is ‘contamination’ of reaction rate k obs and final velocity vs (based on the reversible reaction to reach steady-state equilibrium: vs > 0) with the rate of enzyme degradation k ctrl (based on an inactivation reaction: vs = 0). Y-intercept approaching k ctrl instead of k 6 even though the uninhibited control is not included in the fit is an indication that spontaneous enzyme degradation dominates k obs at low inhibitor concentrations (Fig. 9C). This ‘red flag’ should not be ignored, as it will result in over/underestimation of kinetic parameters. To our knowledge, models to perform an algebraic correction have not been reported. Calculating steady-state inhibition constant Ki* from final velocity vs also results in an underestimation of the steady-state potency because the contribution of spontaneous enzyme degradation to final velocity vs is dominant at low inhibitor concentrations (Fig. 9D). Underestimation of the steady-state potency of reversible covalent inhibitors that have a relatively slow k 6 is more severe than for the less potent counterpart with a faster k 6. We were able to find reasonable estimates of Ki* when the contribution of nonlinearity was significantly smaller than covalent adduct dissociation (k ctrl << k 6). Preincubation time–dependent inhibition (Method III) is a more suitable method to analyze two-step reversible inhibition affected by enzyme instability: it is possible to algebraically correct for enzyme instability in this method (Data Analysis 3C).
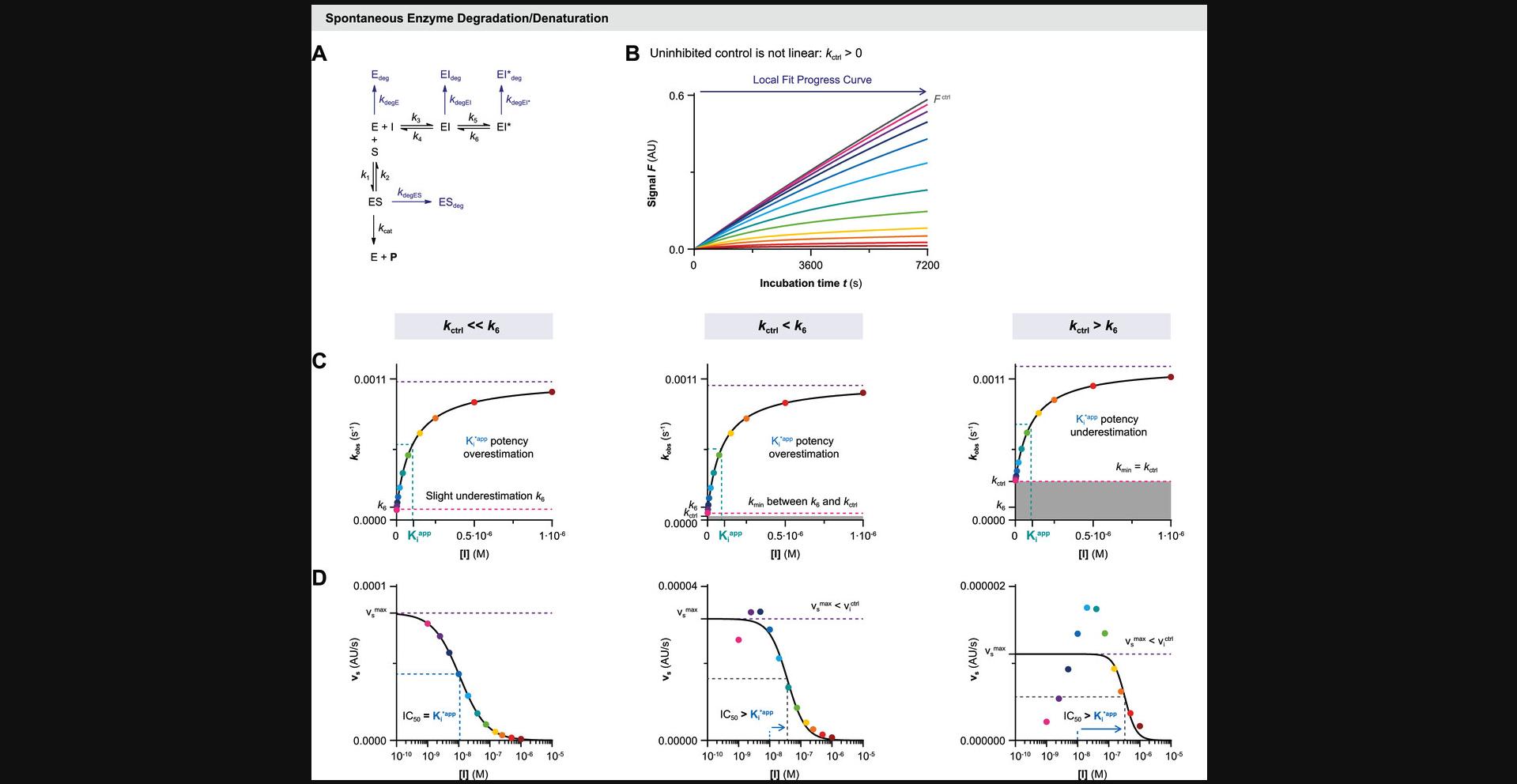
Basic Protocol 4: Two-Step Reversible Covalent Inhibition
Processing of raw data obtained with Basic Protocol I for two-step reversible covalent inhibitors.
1.Plot signal F against incubation time t.
Plot signal (in AU) on the Y-axis against incubation time (in s) on the X-axis for each inhibitor concentration and the controls (Fig. 8B). Product formation in the uninhibited control F ctrl should be linear. Consult Table 3 for troubleshooting of nonlinearity of the uninhibited control. Optionally, perform background correction to correct for assay artifacts such as bleaching and drift that cause a negative final velocity (vs < 0 AU/s) in the fully inhibited control. This correction can be subtraction of the background in the presence of substrate (and inhibitor) but absence of enzyme, or subtraction of the fully inhibited control.
2.Fit F t against t to obtain k obs and vs.
Fit signal F t against incubation time t to Equation II (Fig. 8B) to obtain final product formation velocity vs (in AU/s) and the observed reaction rate k obs (in s−1) from initial equilibrium vi to steady-state equilibrium vs. Do not constrain initial velocity vi or final velocity vs. Also fit the progress curve of the uninhibited control (F ctrl) to validate that product formation is strictly linear (victrl = vsctrl), because algebraic correction for nonlinearity in the uninhibited control is not possible (Fig. 9). The observed rate k obs (in s−1) reflects the exponential reaction rate from initial noncovalent equilibrium (vi) to final steady-state equilibrium (vs).
\begin{equation} {F_{\rm {t}}} = ;{{\rm{v}}{\rm{s}}}t + \frac{{{{\rm{v}}{\rm{i}}} - {{\rm{v}}{\rm{s}}}}}{{{k{{\rm{obs}}}}}}\left[ {1 - {e^{ - {k_{{\rm{obs}}}}t}}} \right] + {F_0} \end{equation}
Equation II for nonlinear regression of user-defined explicit equation Y = (vsX) + (((vi-vs)/kobs)(1-EXP(-kobs*X))) + Y0 with Y = signal F t (in AU) and X = incubation time t (in s) to find Y0 = Y-intercept F 0 = background signal at t = 0 (in AU), vi = initial slope (in AU/s), vs = final slope (in AU/s), and k obs = observed reaction rate k obs (in s−1).
3.Plot and fit vs against [I] to obtain Ki*app.
Apparent steady-state inhibition constant Ki*app (in M) can be calculated from the final velocity vs (obtained in the previous step) reflecting enzyme activity after reaching the steady-state inhibitor equilibrium (reaction completion). Plot the mean and standard deviation of vs (in AU/s) on the Y-axis against inhibitor concentration (in M) on the X-axis and fit to four-parameter nonlinear regression Hill Equation X (Copeland, 2013e) to obtain apparent steady-state inhibition constant Kiapp (in M) (Fig. 8D). Constrain the top to uninhibited velocity vctrl (maximum velocity = vSmax) and the bottom to the fully inhibited vs (vsmin, minimum velocity). For (background-) corrected product formation, vsmin = 0. Accurate values are only obtained when uninhibited product formation is strictly linear (k ctrl = 0) or when the rate of spontaneous inactivation k ctrl is much smaller than the covalent dissociation k 6 (Fig. 9). Validate that vs is not driven by spontaneous enzyme degradation (k ctrl << k 6) by also fitting without constraints for vSmax. Calculate steady-state inhibition constant Ki (in M) with Sample Calculation 7.
\begin{equation} {{\rm{v}}{\rm{s}}} = {\rm{v}}{\rm{s}}^{{\rm{min}}} + \frac{{{{\rm{v}}^{{\rm{ctrl}}}} - {\rm{v}}{\rm{s}}^{{\rm{min}}}}}{{1 + {{\left( {\frac{{\left[ {\rm{I}} \right]}}{{{\rm{K}}{\rm{i}}^{{\rm{*app}}}}}} \right)}^h}}} \end{equation}
Equation X for nonlinear regression of four-parameter dose-response equation Y = Bottom + (Top-Bottom)/(1 + (X/IC50)^HillSlope) with Y = final product formation velocity vs (in AU/s), X = inhibitor concentration (in M), Bottom = velocity in fully inhibited control vsmin (in AU/s) and Top = maximum velocity in uninhibited control vctrl (in AU/s) to find Hillslope = Hill coefficient h (unitless) and IC50 = apparent steady-state inhibition constant Ki*app (in M).
4.Optional : Plot and fit k obs against [I] to obtain Kiapp, k 5, and k 6.
This is an optional data processing step to obtain kinetic parameters by fitting to the observed rate k obs (obtained in Data Analysis 1C , step 2), and is used to validate Kiapp values found in the previous step, to check if nonlinearity in the uninhibited control k ctrl (in s−1) affects the fit, and/or to generate experimental k 5 and k 6 values to use in kinetic simulations. Plot the mean and standard deviation of k obs (in s−1) on the Y-axis against inhibitor concentration (in M) on the X-axis (Fig. 8C). Exclude k obs of uninhibited control (k ctrl) from the fit. Fit k obs against inhibitor concentration to Equation XI to obtain rate constants for the covalent association k 5 (in s−1) and covalent dissociation k 6 (in s−1), as well as apparent noncovalent inhibition constant Kiapp (in M) reflecting the rapid (initial) noncovalent equilibrium. Use the inhibitor concentration after reaction initiation by enzyme addition (in the final solution). Accurate values are only obtained when uninhibited product formation is strictly linear (k ctrl = 0). Y-intercept approaching k ctrl despite the uninhibited control not being included in the fit is a red flag that should not be ignored, as this is indicative of spontaneous enzyme degradation rather than k 6 dominating k obs at low inhibitor concentrations, for which algebraic corrections are not available (Fig. 9). Calculate noncovalent inhibition constant Ki (in M) with Sample Calculation 3 and proceed to calculate steady-state inhibition constant Ki (in M) with Sample Calculation 8. Optionally, perform step 6 of Data Analysis 1A to obtain apparent noncovalent inhibition constant Kiapp (in M) from the initial velocity vi (obtained in Data Analysis Protocol 1C step 2).
\begin{equation} {k_{{\rm{obs}}}} = {k_6} + \frac{{{k_5}{\rm{;}}\left[ {\rm{I}} \right]}}{{{{\rm{K}}_{\rm{i}}}^{{\rm{app}}} + \left[ {\rm{I}} \right]}} \end{equation}
Equation XI for nonlinear regression of user-defined explicit equation Y = Y0 + ((kmax*X)/((Kiapp) + X)) with Y = observed reaction rate k obs (in s−1) and X = inhibitor concentration (in M) to find Y0 = covalent dissociation rate constant k 6 (in s−1), kmax = covalent association rate constant k 5 (in s−1) and Kiapp = Apparent inhibition constant Kiapp (in M).
5.Optional : Validate experimental kinetic parameters with kinetic simulations.
Proceed to Kinetic Simulations 1 to compare the experimental progress curves to the progress curves simulated with scripts KinGen and KinDeg to confirm that the calculated kinetic constants are in accordance with the experimental data. Experimental estimates of k 5 and k 6 are generated in the previous step of this protocol.
Data Analysis 1D: Algebraic Correction for Substrate Depletion in Progress Curve Analysis for Two-Step Irreversible Covalent Inhibition
Scientists from BioKin and Pfizer (Kuzmič et al., 2015) derived an algebraic model for two-step irreversible covalent inhibitors to correct for nonlinearity caused by substrate depletion (Fig. 10A). Substrate depletion causes a nonlinearity in the uninhibited control because the unbound substrate concentration is no longer constant ([S]t < [S]0) when a significant fraction of the substrate has been converted into product ([P]t > 0.1[S]0). The contribution of substrate depletion to the progress curve is directly related to the enzyme activity, as >10% substrate conversion is more likely to be exceeded when enzyme activity is high (Fig. 10B). Algebraic correction is performed by globally fitting all progress curves in presence of inhibitor to Equation III with shared values for k inact and KIapp (Fig. 10C and 10D). Substrate depletion should be the only factor contributing to nonlinearity, because the uninhibited control is not included in the global fit. Violation of this (and other) assumption requires data analysis by numerical solving (Kuzmič, 2015).
![Details are in the caption following the image Data Analysis 1D: Algebraic correction for substrate depletion in progress curve analysis for two-step irreversible covalent inhibition. Simulated with KinSubDpl for inhibitor C with 100 pM enzyme and 10 nM substrate S1. (A) Enzyme dynamics for two-step irreversible covalent inhibition. Algebraic correction for substrate depletion is restricted to a Hit-and-Run model (E + S → E + P) for product formation. (B) Substrate depletion ([P]<sub>t</sub> > 0.1[S]<sub>0</sub>, blue area) results in a decrease of product formation in the uninhibited control (solid line) compared to product formation, assuming substrate conversion does not affect product formation rates (dashed line, simulated with KinGen). The contribution of substrate depletion to nonlinearity increases with higher enzyme activity (less inhibition). (C) Time-dependent product formation in the absence of inhibitor F<sup>ctrl</sup> or in presence of inhibitor with time-dependent loss of enzyme activity due to substrate depletion. Inhibitor-treated progress curves are globally fitted to Equation III with shared values for k<sub>inact</sub> and K<sub>I</sub><sup>app</sup>. (D) Equation III. Algebraic model to correct for substrate depletion at low substrate concentrations (Kuzmič et al., 2015). F<sub>0</sub> = Y-intercept = background signal at reaction initiation (in AU). r<sub>P</sub> = product coefficient for detected signal F per formed product [P] (in AU/M). k<sub>sub</sub> = reaction rate constant for Hit-and-Run model of enzymatic product formation E + S → E + P (in M<sup>−1</sup>s<sup>−1</sup>).](https://static.yanyin.tech/literature_test/cpz1419-fig-0010-m.jpg)
Warnings and remarks
The authors demonstrate their algebraic model to correct for substrate depletion with the EGFR inhibitor afatinib in a homogeneous kinase activity assay. A bisubstrate kinase activity assay is different from our simulations with a single substrate, but this algebraic model can be applied in both systems: product formation in single-substrate as well as bisubstrate reactions can be simplified to a Hit-and-Run model (E + S → E + P) with rate constant k sub = k cat/KM (in M−1s−1) as long as the substrate concentration is far below its KM ([S] < 0.1KM) (Fig. 10A). The accuracy of k inact and KI was very good with low substrate concentrations ([S] ≤ 0.01KM). A slightly higher substrate concentration ([S] ≥ 0.1KM) resulted in underestimation of k inact and overestimation of KI, but a good estimation of overall second-order inactivation rate constant k inact/KI. Importantly, a calibration/titration (Dharadhar et al., 2019; Janssen et al., 2019) should be performed prior to data analysis to determine product coefficient r P (in AU/M) that transforms the detected signal F t (in AU) into product concentration [P]t (in M).
Basic Protocol 5: Two-Step Irreversible Covalent Inhibition With Substrate Depletion
Processing of raw data obtained with Basic Protocol I for two-step irreversible covalent inhibitors with nonlinearity in the uninhibited control resultant from substrate depletion ([P]t < 0.1[S]0).
Before you start , validate compliance with essential assay reaction conditions such as the Hit-and-Run model. This algebraic correction for substrate depletion (Kuzmič et al., 2015) has additional requirements for assay conditions, and is only compatible with two-step irreversible inhibition (Fig. 10). Validate that the product formation reaction complies with the Hit-and-Run model E + S → E + P (Fig. 10A): substrate concentration must be far below the KM ([S]0 < 0.1KM) to calculate the pseudo-first order reaction rate constant for enzymatic product formation k sub = k cat/KM (M−1s−1). Observed nonlinearity in the uninhibited control should be fully attributed to substrate depletion. Convert the maximum signal F ctrl (in AU) into product concentration (in M) using the product coefficient r P (in AU/M product) as determined in a separate product calibration experiment (Dharadhar et al., 2019; Janssen et al., 2019). Validate that the total substrate conversion to product exceeds 10% of the initial substrate concentration ([Pctrl]t > 0.1[S]0), and that substrate depletion is the only factor that contributes to the observed nonlinearity: uninhibited product formation should be linear when incubation times are shorter ([P]t < 0.1[S]0) or enzyme concentration is lower. Alternatively, perform kinetic analysis by numeric solving if one or more assumptions are violated (Kuzmič, 2015).
\begin{equation*} {\left[ {\rm{P}} \right]t} = \frac{{{F{\rm {t}}} - {F_0}}}{{{r_{\rm{P}}}}} \end{equation*}
Calculate: Pt=(Ft-F0)/rp with Pt = product concentration at the end of the incubation [P]t (in M), Ft = signal in uninhibited control at the end of the incubation time F t (in AU), F0 = substrate background signal F 0 (in AU) and rp = product coefficient r P (in AU/M product).
1.Plot signal F against incubation time t.
Plot signal (in AU) on the Y-axis against incubation time (in s) on the X-axis for each inhibitor concentration (Fig. 10C). Label the columns with the inhibitor concentration (in M).
2.Perform background correction.
Correct for assay artifacts such as fluorescence bleaching and drift that cause a declining signal in the fully inhibited control. This correction can be subtraction of the time-dependent background in absence of enzyme but in presence of substrate (and inhibitor), or subtraction of the fully inhibited control. Consult the guidelines of your data fitting software for instructions on background corrections (GraphPad Prism; see Internet Resources).
3.Globally fit F t against t to obtain k inact and KIapp.
Globally fit the progress curves of time-dependent signal F t for all inhibitor concentrations to Equation III. Exclude the dataset of the fully inhibited control from the fit. Constrain [E]0 (in M), [S]0 (in M), and [I] = [I]0 (in M) to their theoretical values. Originally, [I]0 was locally optimized (Kuzmič, 2015), but we used fixed values of [I]0 in GraphPad Prism. Constrain product coefficient r P (in AU/M product) to the value determined in a separate product calibration experiment. Constrain k inact, KI, and k sub to a shared value for all datasets that must be greater than 0, and provide initial values that are in the anticipated range. Note that Equation III is in agreement with equation C.16 of the original publication (Kuzmič et al., 2015), but [I]0 and k inact were unintentionally displaced in Equation III. Calculate inactivation constant KI (in M) and irreversible covalent inhibitor potency k inact/KI (in M−1s−1) with Sample Calculations 1 and 2.
\begin{eqnarray} {F_{\rm {t}}} &&= {F_0} + {r_{\rm{P}}}{\left[ {\rm{S}} \right]0}\left\{ {1 - {e^{ - \beta \left( {1 - {e^{ - \alpha t}}} \right);}}} \right\}\nonumber\\ \alpha &&= \frac{{{k{{\rm{inact}}}}{\rm{;}}\left[ {\rm{I}} \right]}}{{{{\rm{K}}{\rm{I}}}^{{\rm{app}}} + \left[ {\rm{I}} \right]}}\nonumber\\ \beta &&= \left( {\frac{{{{\left[ {\rm{E}} \right]}0};{k{{\rm{sub}}}}}}{{{k{{\rm{inact}}}}}}} \right)\left( {\frac{{{{\rm{K}}_{\rm{I}}}^{{\rm{app}}}}}{{\left[ {\rm{I}} \right]}}} \right)\nonumber\\ \end{eqnarray}
Equation III for nonlinear regression of user-defined explicit equation:
- a = kinact*I0/(I0+KIapp)
- b = (E0ksub/kinact)(KIapp/I0)
- P = S0*(1−exp(−b*(1−exp(−a*X))))
- Y = Y0+(rp*P)
with Y = time-dependent signal F t (in AU), X = incubation time t (in s), rp = product coefficient rP (AU/M product), E0 = maximum unbound enzyme concentration at reaction initiation [E]0 (in M), S0 = maximum unbound substrate concentration at reaction initiation [S]0 (in M) and I0 = maximum unbound inhibitor concentration [I] (in M) to find globally shared values for ksub = product formation rate constant k sub = k cat/KM (in M−1s−1), kinact = maximum rate of inactivation k inact (in s−1) and KIapp = apparent inactivation constant KIapp (in M).
4.Optional : Validate experimental kinetic parameters with kinetic simulations.
Proceed to Kinetic Simulations 1 to compare the experimental progress curves to the progress curves simulated with script KinSubDpl (using experimental rate constant k inact = k 5) to confirm that the calculated kinetic constants are in accordance with the experimental data.
METHOD II: INCUBATION TIME–DEPENDENT POTENCY IC50(t)
The observed potency of irreversible inhibitors increases with longer (pre)incubation time, as more enzyme is irreversibly bound. In this method, sometimes dubbed ‘the Krippendorff method’, the time-dependence of potency IC50(t) is utilized to directly find the relevant kinetic parameters for two-step irreversible covalent inhibition. Contrary to progress curve analysis (Method I), this method is compatible with quenched/stopped assays that require a development/separation/quenching step before read-out, as continuous measurement of product formation is not required (but optional).
The incubation time–dependent potency IC50(t) reflects the inhibitor concentration resulting in a 50% decrease of cumulative product formed F t during incubation compared to cumulative product formed in the uninhibited control F ctrl. Enzymatic product formation is initiated by enzyme addition without preincubation of enzyme and inhibitor (Fig. 11A). Fractional cumulative product formation F t/F ctrl decreases with longer incubation times (Fig. 11B). Importantly, this does not reflect the current enzyme activity because read-out F t reflects that the cumulative product formed during incubation will be ‘contaminated’ with product that was formed before full inhibition was reached. Consequently, incubation time–dependent potency IC50(t) calculated from the fractional product formation F t/F ctrl against inhibitor concentration will increase with longer incubation times (for slow-binding inhibitors), but will underestimate the potency compared to the values based on the current enzyme activity [E+ES]t/[E]0 (Fig. 11C). IC50(t) does not approach Ki*app (two-step reversible inhibition) or ½[E]0 (irreversible inhibition) at infinite incubation times.
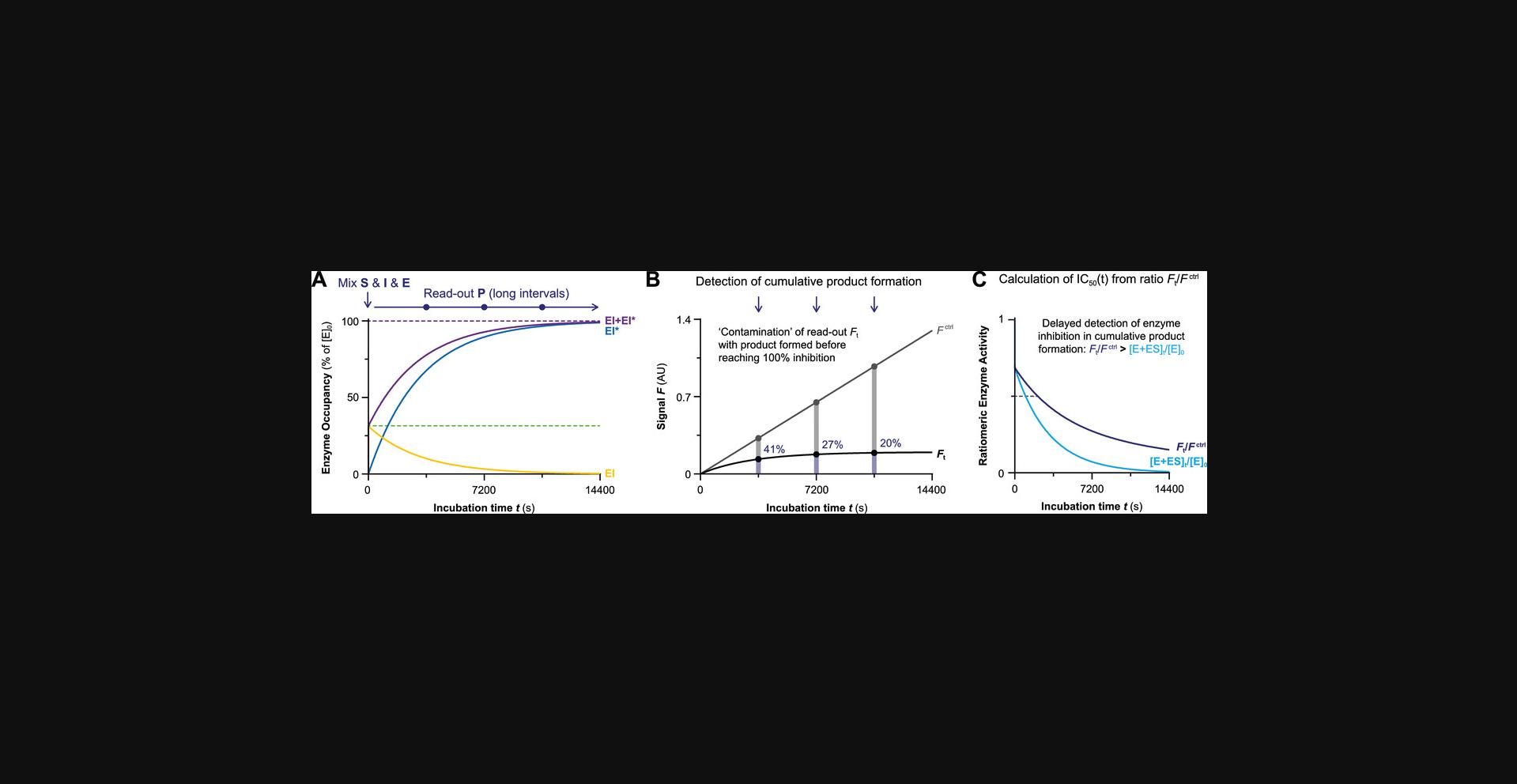
An implicit algebraic model based on multipoint IC50(t) values has been derived (Krippendorff, Neuhaus, Lienau, Reichel, & Huisinga, 2009) for two-step irreversible covalent inhibitors (Data Analysis 2). Additionally, a two-point IC50(t) method for two-step irreversible covalent inhibitors as well as a one-point IC50(t) method for one-step irreversible covalent inhibitors have been reported in a preprint (Kuzmič, 2020b). To our knowledge, algebraic methods to calculate Ki*app (two-step reversible covalent inhibitors) from (endpoint) IC50(t) values have not been reported.
Basic Protocol 6: Incubation Time-Dependent Potency IC50(t)
The below protocol provides a generic set of steps to accomplishing this type of measurement.
Materials
- 1× Assay/reaction buffer supplemented with co-factors and reducing agent
- Active enzyme, 4× solution in assay buffer
- Competitive substrate with continuous or quenched read-out, 4× solution in assay buffer
- Positive control: vehicle/solvent as DMSO stock, or 2% solution in assay buffer
- Negative control: known inhibitor or alkylating agent as DMSO stock, or 2× solution in assay buffer
- Inhibitor: as DMSO stock, or serial dilution of 2× solution in assay buffer with 2% DMSO
- Optional : Development/quenching solution
- 384-well low volume microplate with nonbinding surface (e.g., Corning 3820 or 4513) for incubation and/or read-out
- Optical clear cover/seal (e.g., Perkin Elmer TopSeal-A Plus, #6050185, Corning 6575 Universal Optical Sealing Tape or Duck Brand HP260 Packing Tape) for continuous read-out, or a general microplate cover/lid (e.g., Corning 6569 Microplate Aluminum Sealing Tape) for non-continuous read-out
- 1.5 ml (Eppendorf) microtubes to prepare stock solutions
- Optional : 96-well microplate to prepare serial dilution of inhibitor concentration
- Optional : Microtubes to perform incubations (e.g., Eppendorf Protein Lobind Microtubes, #022431018)
- Microplate reader equipped with appropriate filters to detect product formation (e.g., CLARIOstar microplate reader)
- Optional : Automated (acoustic) dispenser (e.g., Labcyte ECHO 550 Liquid Handler acoustic dispenser)
Before you start , optimize assay conditions in the uninhibited control to ensure compliance with assumptions and restrictions (Fig. 13) as outlined for Basic Protocol I. It is crucial to ensure that uninhibited product formation is linear with incubation time for the duration of the measurement: no enzyme degradation (k deg = 0) or other factors contributing to a nonlinearity in product formation in the uninhibited control (k ctrl = 0) are allowed, as correction for nonlinearity is not possible in Data Analysis 2. This method is compatible with homogeneous (continuous) assays but also with assays that require a development/quenching step to visualize formed product.
1.Add inhibitor or control (e.g., 0.2 µl) and assay buffer (e.g., 10 µl) to each well with the uninhibited control for full enzyme activity containing the same volume of vehicle/solvent instead of inhibitor as outlined in step 1 of Basic Protocol I.
Typically, measurements are performed in triplicate (or more replicates) with at least 8 inhibitor concentrations spanning the IC50(t). Inhibitor concentrations might need optimization, but a good starting point is [I] = 0.1-5 × IC50(t) at the shortest incubation time t. Alternatively, larger-volume incubations can be performed in (Eppendorf) Protein Lobind microtubes, from which aliquots are transferred to a microplate after the indicated incubation time. Whether incubation in tube or plate is performed is a matter of personal preference, compatibility with lab equipment and automation, and convenience of dispensing small volumes
2.Add substrate in assay buffer to each well (e.g., 5 µl of 4× solution) and homogenize the solutions by gentle shaking (1 min at 300 rpm).
The order of substrate or inhibitor addition is not important per se , as long as DMSO stocks are added prior to buffered (aqueous) solutions and the enzyme is the last reagent to be added, to avoid unintentional preincubation (Fig. 13A). Inhibitor binding mode must be competitive with substrate. Optionally, gently centrifuge the plate or microtubes (1 min at 1000 rpm) to ensure assay components are not stuck at the top of the well.
3.Add active enzyme in assay buffer to each well (e.g., 5 µl of 4× solution) or tube as outlined in step 3 of Basic Protocol I.
The accuracy of the measurement improves if the incubation time is monitored precisely.
4.Seal the wells by applying an (optical clear) cover or lid, or close the caps of microtubes to prevent evaporation of assay components during incubation.
5.Optional : Transfer aliquots (e.g., 20 µl) from the reaction mixture to the microplate after each time point, if incubation is performed in large volumes (in Protein Lobind microtubes or 96-well NBS plate) rather than incubation of replicates in a 384-well microplate.
6.Quenching : Add development solution to the reaction mixture in the microplate to quench the product formation reaction for assay formats that require a development/quenching step to visualize formed product.
Incubation time t is the elapsed time between reaction initiation by enzyme addition (step 3) and (optional) quenching of the enzyme activity by addition of development/quenching solution (step 6).
7.Measure formed product after incubation by detection of the product read-out in microplate reader.
Follow manufacturer's advice on waiting time after addition of development solution before read-out. A typical assay measurement window is >2 hr, measuring cumulative product formation every 5-30 min (Fig. 11). The best results are obtained when inhibitor concentrations cover at least 50% of the DRC at all incubation times (Fig. 12C) and there is a significant decrease from the earliest to the last IC50(t) value (Fig. 12D).
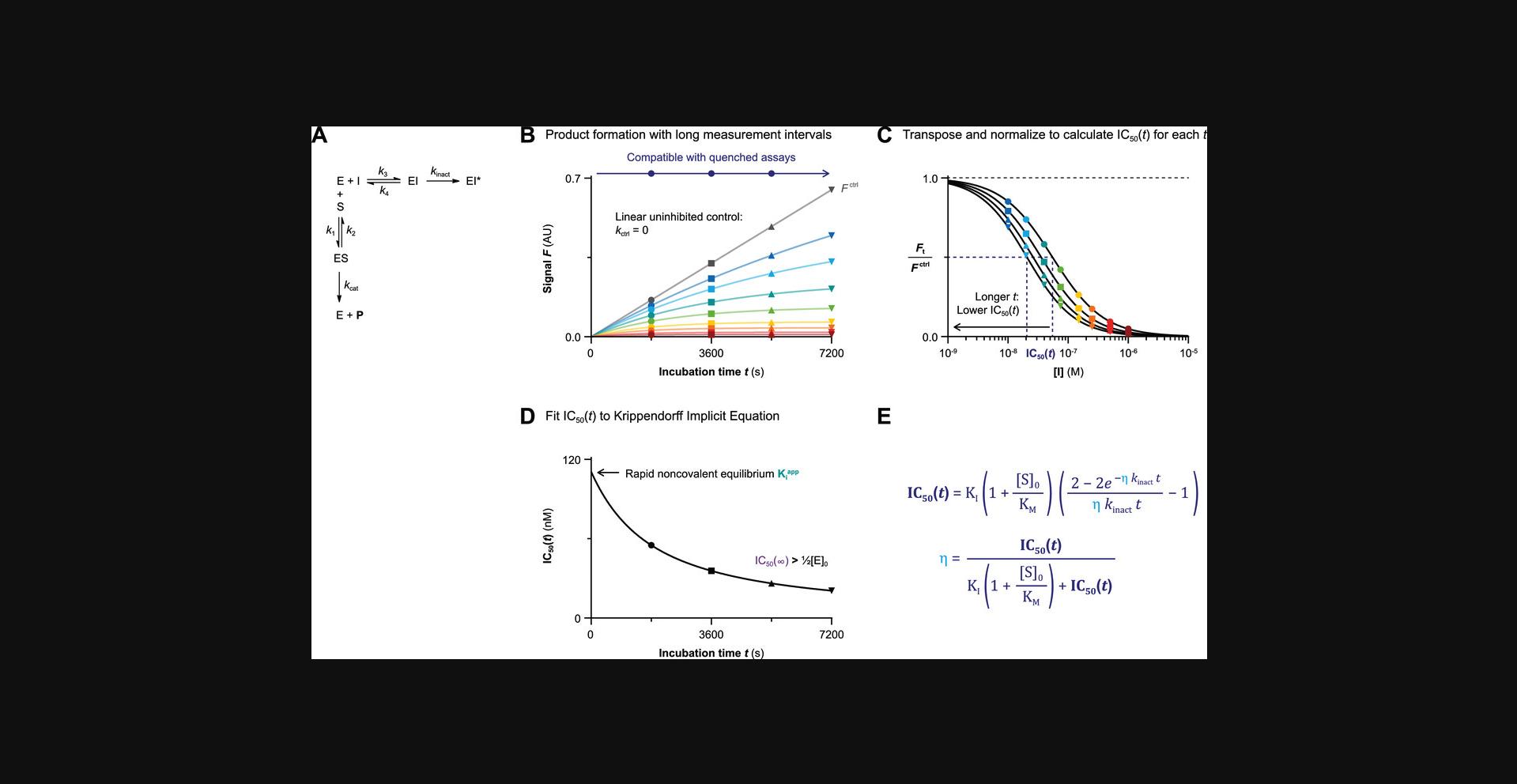
8.Proceed to Basic Data Analysis Protocol 2 to calculate relevant kinetic parameters for two-step irreversible covalent inhibition
| Data Analysis Protocol | |||
|---|---|---|---|
| EXP Conditions | 2-step IRREV | 1-step IRREV | 2-step REV |
| kctrl = 0 | 2 | – | – |
Exemplary assay concentrations.
| Concentration during incubation t | |||
|---|---|---|---|
| [stock] | V (µl) | [conc]t | |
| Enzyme | 4 nM | 5 | 0.99 nM |
| Inhibitor | 20 nM | 10.2 | 10.10 nM |
| Substrate | 4 µM | 5 | 0.99 µM |
| Total | 20.2 | ||
Data Analysis 2: Incubation Time–Dependent Potency IC50(t) for Two-Step Irreversible Covalent Inhibition
Krippendorff and co-workers report an algebraic model to calculate k inact and KI of irreversible covalent inhibitors from the incubation time–dependent potency IC50(t) after multiple incubation times (Krippendorff et al., 2009). Detection of cumulative product formation after several incubation times is compatible with continuous assays, but more importantly also with stopped/quenched assays that require a development step to visualize product formation (Fig. 12A and 12B). Incubation time–dependent potency IC50(t) is calculated for each incubation time from fractional product formation F t/F ctrl (Fig. 12C) and plotted against the incubation time (Fig. 12D). Finally, the authors derived implicit algebraic Equation IV (Fig. 12E) to calculate k inact and KI from the incubation time–dependent potency IC50(t). This method is restricted to substrate-competitive irreversible (multi-step) covalent inhibitors: k inact and KI do not have a biological meaning for reversible inhibitors or for one-step covalent inhibitors.
Warnings and remarks
This method requires software (e.g., GraphPad Prism) that allows fitting a model defined by an implicit equation (where Y appears on both sides of the equal sign). Product formation in the uninhibited control should be strictly linear (k ctrl = 0): normalization of cumulative product formation (F t/F ctrl) does not correct for spontaneous loss of enzyme activity or substrate depletion. It is relatively easy to miss violations of this assumption because nonlinearity in the uninhibited control (k ctrl > 0) is not evident from visual inspection of the dose-response curves (Fig. 12B). Violation of this assumption results in a significant underestimation of k inact and KI values, also when nonlinearity is relatively small (k ctrl << k inact) (Fig. 13A).
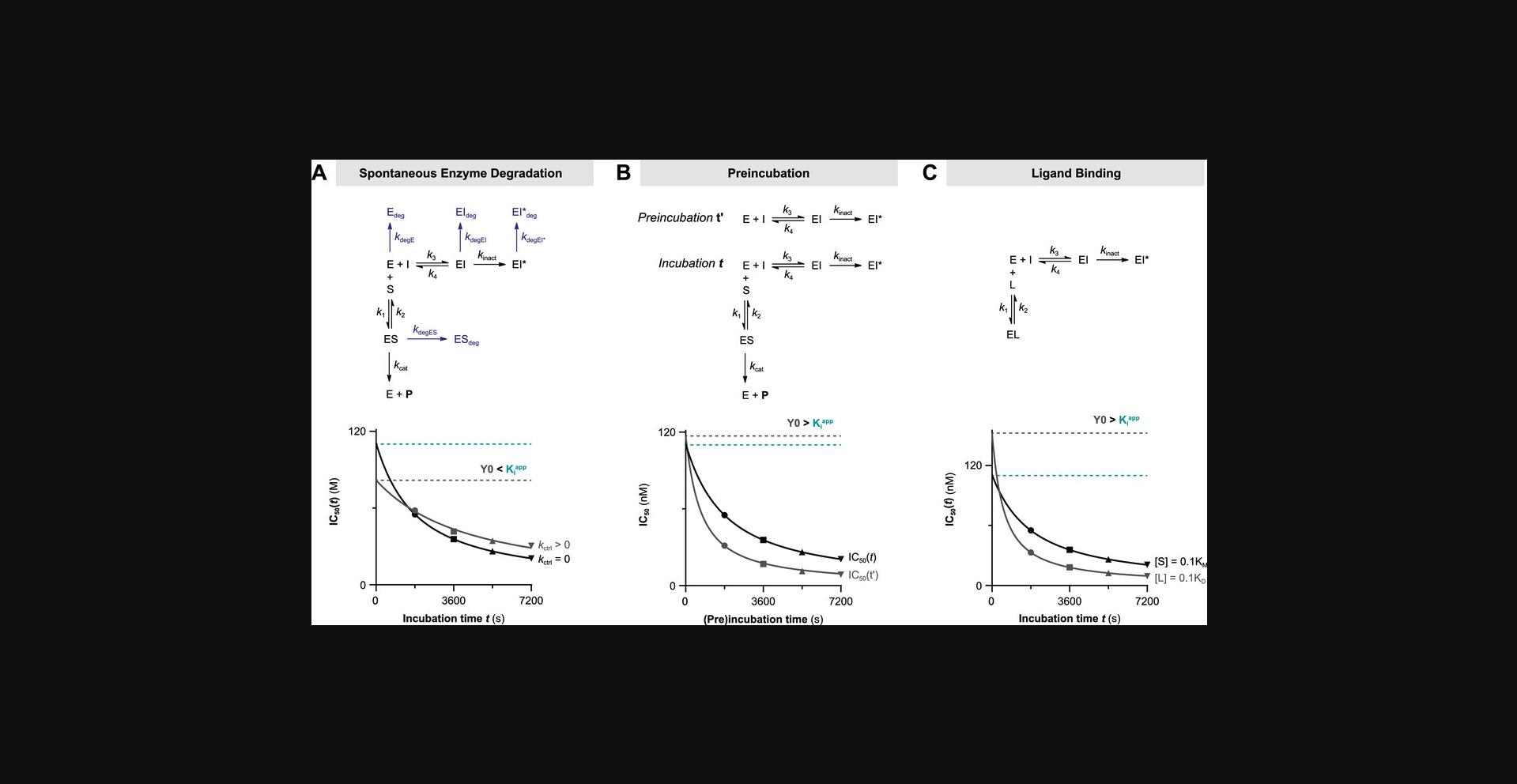
Another important assumption is that the onset of product formation and enzyme inhibition occur simultaneously: inhibition and product formation are both initiated by addition of enzyme, without preincubation of enzyme and inhibitor prior to substrate addition. Unfortunately, numerous publications refer to preincubation of enzyme and inhibitor as ‘incubation’, resulting in the understandable but incorrect fitting of preincubation time–dependent potency IC50(t′) to the Krippendorff model (Kuzmič, 2020b). Preincubation-dependent potency IC50(t′) is calculated from product formation velocity vt′, reflecting the enzyme activity after preincubation rather than cumulative product formation F t/F ctrl. Enzyme activity vt′ is not ‘contaminated’ by product formed prior to read-out because product formation is initiated after the preincubation. Furthermore, substrate does not compete with inhibitor for enzyme binding during preincubation. Fitting IC50(t′) values to the Krippendorff model resulted in an overestimation of k inact and an overestimation of the overall inactivation potency k inact/KI (Fig. 13B).
This method is not compatible with ligand binding competition assays (such as the Lanthascreen kinase binding assay) where inhibitor binding competes with ligand (tracer) binding to form enzyme-ligand complex EL as the detectable product (Fig. 13C). The enzyme-ligand equilibrium after incubation in presence of inhibitor reflects the current inhibitor competition and is unaffected by binding equilibria prior to read-out (not cumulative). Furthermore, unbound enzyme is not released after formation of product EL, thereby limiting the product formation to a single turnover per enzyme. Fitting IC50(t) values obtained in ligand-binding assays (simulated with k cat = 0) to the Krippendorff model result in overestimation of k inact and/or unstable parameters.
Basic Protocol 7: Two-Step Irreversible Covalent Inhibition
Processing of raw data obtained with Basic Protocol I or Basic Protocol II for two-step irreversible covalent inhibitors.
1.Plot signal F against incubation time t.
Plot cumulative signal (in AU) on the Y-axis against incubation time (in s) on the X-axis for each inhibitor concentration and for the controls (Fig. 12B). Label the columns with the inhibitor concentration (in M). It is not possible to algebraically correct for spontaneous loss of enzyme activity. Validate that the product formation in the uninhibited control F ctrl is linear (vi = vs) by performing steps 1-3 of Basic Data Analysis Protocol 1A with k obs = k ctrl. Consult Table 3 for troubleshooting of nonlinearity of the uninhibited control.
2.Perform background correction.
Correct for assay artifacts such as fluorescence bleaching and drift that cause a declining signal in the fully inhibited control. This correction can be subtraction of the time-dependent background in absence of enzyme but in presence of substrate (and inhibitor), or subtraction of the fully inhibited control.
3.Transpose to plot signal F against inhibitor concentration [I].
For each incubation time, transpose the X and Y values to plot signal F t (in AU) on the Y-axis against inhibitor concentration (in M) on the X-axis. Also include product formation in the uninhibited control F ctrl ([I] = 0).
4.Normalize F t/F ctrl.
Normalize F t (in AU) to lowest value = 0 (in AU) and highest value = uninhibited product formation F ctrl (in AU) to obtain fractional product formation in presence of inhibitor F t/F ctrl (Fig. 12C). Consult the guidelines of your data fitting software for instructions on data normalization to the positive and negative controls (GraphPad; see Internet Resources).
5.Plot and fit F t/F ctrl against [I] to obtain the incubation time–dependent potency IC50(t).
Plot the dose-response curve of fractional signal F t/F ctrl against inhibitor concentration (in M), and fit to four-parameter nonlinear regression Hill Equation XII (Copeland, 2013e) to obtain the incubation time–dependent potency IC50(t) (in M) (Fig. 12C). Use the inhibitor concentration during incubation: after reaction initiation by enzyme addition but before (optional) addition of development solution (Basic Protocol II , step 3).
\begin{equation} \frac{{{F_{\rm {t}}}}}{{{F^{{\rm{ctrl}}}}}} = \frac{1}{{1 + {{\left( {\frac{{{\rm{I}}{{\rm{C}}_{50}}\left( t \right)}}{{\left[ {\rm{I}} \right]}}} \right)}^h}}} \end{equation}
Equation XII for nonlinear regression of four-parameter dose-response equation Y = Bottom + (Top-Bottom)/(1 + (IC50/X)^HillSlope) with Y = fractional product signal F t/F ctrl (unitless), X = inhibitor concentration [I] (in M), Bottom = normalized fully inhibited product signal = 0 (unitless), and Top = normalized uninhibited product signal F ctrl /F ctrl = 1 (unitless) to find Hillslope = Hill coefficient h (unitless) and IC50 = incubation time–dependent potency IC50(t) (in M).
6.Plot and fit IC50(t) against t to obtain k inact and KI.
Plot the mean and standard deviation of IC50(t) (in M) on the Y-axis against incubation time t (in s) on the X-axis (Fig. 12D). The rate of covalent bond formation at saturating inhibitor concentration k inact and inactivation constant KI are obtained by solving implicit Equation IV (Krippendorff et al., 2009) (Fig. 12E). Use the substrate concentration during incubation (Basic Protocol II , step 3): after reaction initiation by enzyme addition but before (optional) addition of development/quenching solution. It is important that the Michaelis constant KM be accurate for the reaction conditions (buffer, temperature, substrate), as this value is directly used to correct inactivation constant KI for substrate competition. Consult the guidelines of your data-fitting software (GraphPad; see Internet Resources for website) for instructions on solving implicit equations (where Y appears on both sides of the equal sign). Proceed to Sample Calculation 2 to calculate irreversible covalent inhibitor potency k inact/KI (in M−1s−1) with propagation of error.
\begin{equation} {\rm{I}}{{\rm{C}}{50}}\left( t \right) = {\rm{;}}{{\rm{K}}{\rm{I}}}\left( {1 + \frac{{{{\left[ {\rm{S}} \right]}0}}}{{{{\rm{K}}{\rm{M}}}}}} \right)\left( {\frac{{2 - 2{{\rm{e}}^{ - {\rm{\eta }}{k_{{\rm{inact}}}}t}}}}{{{\rm{\eta }}{k_{{\rm{inact}}}}t}} - 1} \right){\rm{;;}}with{\rm{;;\eta }} = \frac{{{\rm{I}}{{\rm{C}}{50}}\left( t \right)}}{{{{\rm{K}}{\rm{I}}}\left( {1 + \frac{{{{\left[ {\rm{S}} \right]}0}}}{{{{\rm{K}}{\rm{M}}}}}} \right) + {\rm{I}}{{\rm{C}}_{50}}\left( t \right)}} \end{equation}
Equation IV for nonlinear regression of user-defined implicit equation Y=(KI*(1+(S/KM)))(((2-(2EXP(- (Y/((KI*(1+(S/KM)))+Y))kinactX)))/((Y/((KI*(1+(S/KM)))+Y))kinactX))-1), with Y = incubation time–dependent potency IC50(t) (in M), X = incubation time t (in s), S = maximum unbound substrate concentration at reaction initiation [S]0 (in M), and KM = Michaelis constant KM (in M) to find kinact = inactivation rate constant k inact (in s−1) and KI = inactivation constant KI (in M).
7.Optional : Validate experimental kinetic parameters with kinetic simulations.
Proceed to Kinetic Simulations 1 to compare the experimental read-out to the product formation simulated with scripts KinGen and KinDeg (using experimental rate constant k inact = k 5) to confirm that the calculated kinetic constants are in accordance with the experimental data and found IC50(t) values.
METHOD III: PREINCUBATION TIME–DEPENDENT INHIBITION WITHOUT DILUTION
Preincubation of enzyme and inhibitor prior to initiation of product formation by addition of substrate is an established method for kinetic analysis of slow-binding (ir)reversible (covalent) inhibitors (Copeland, 2013b; Ito et al., 1998). In the benchmark protocol by Ito and co-workers, a low substrate concentration ([S] << KM) is added in a relatively small volume (Vsub << Vt′) to keep the noncovalent enzyme-inhibitor E + I <-> EI equilibrium intact. However, (partial) disruption of the noncovalent equilibrium does not affect the accuracy of preincubation experiments for irreversible inhibition, as is illustrated by Method IV. Product formation is inhibited by formation of EI and EI* during preincubation in absence of competing substrate (Fig. 14A). Preincubation time–dependent product formation velocity vt′ reflects the total inhibition by noncovalent as well as covalent inhibitor binding, and is calculated after a relatively short incubation time (t << t′) to minimize additional (time-dependent) inhibition of enzyme activity during incubation resultant from enzyme-inhibitor complex/adduct formation during incubation (Fig. 14B). Enzyme activity after preincubation in the presence of time-dependent inhibitors vt′ decreases exponentially from rapid (initial) equilibrium Kiapp (Y-intercept: vi) to reach a plateau at reaction completion (t′ > 5t½), corresponding to the steady-state equilibrium (vs > 0) or inactivation (vs = 0) (Fig. 14C). Observed rate of reaction completion k obs (from enzyme activity without preincubation vi to final enzyme activity vs) is obtained by fitting to bounded exponential decay Equation V (Fig. 14D). Importantly, this equation fits enzyme activity vt′ (in AU/s) rather than directly fitting product signal F (in AU).
![Details are in the caption following the image Method III: Preincubation time–dependent inhibition without dilution. Simulated with KinGen for 1 pM enzyme and 100 nM substrate S1. (A) Enzyme is preincubated with inhibitor to form noncovalent complex EI and covalent adduct EI* in absence of competing substrate, followed by addition of substrate. Addition of a low substrate concentration in a small volume to avoid disruption of the noncovalent E + I <-> EI equilibrium. Simulated for 50 nM inhibitor C with preincubation t′ = 1800 s. (B) Preincubation time–dependent enzyme activity v<sub>t′</sub> is obtained from the slope of (initial) linear product formation velocity with a short incubation time t relative to preincubation t′ to minimize ΔEI* formation after substrate addition. This measurement is performed separately for each preincubation time, thus requiring more material than incubation time–dependent inhibition protocols with continuous product read-out. Simulated for 50 nM inhibitor C with preincubation t′ = 1800 s. (C) Enzyme activity v<sub>t′</sub> of time-dependent inhibitors decreases exponentially from rapid (initial) equilibrium K<sub>i</sub><sup>app</sup> (Y-intercept = enzyme activity without preincubation v<sub>i</sub>) to reaching reaction completion (t′ > 5t½): inactivation for irreversible inhibitors (v<sub>s</sub> = 0) and steady-state equilibrium K<sub>i</sub><sup>*app</sup> for reversible inhibitors (v<sub>s</sub> > 0). Enzyme activity without preincubation v<sub>i</sub> equals the uninhibited enzyme activity v<sup>ctrl</sup> for one-step inhibitors and for two-step inhibitors at non-saturating concentration ([I] << K<sub>i</sub><sup>app</sup>). Simulated for 50 nM one-step reversible inhibitor A, two-step reversible inhibitor B, one-step irreversible inhibitor D, and two-step irreversible inhibitor C. (D) General bounded exponential decay Equation V to fit preincubation time–dependent enzyme activity v<sub>t′</sub> (in AU/s) against preincubation time t′ (in s). Parameters are constrained depending on the inhibitor binding mode. Irreversible inhibition: v<sub>s</sub> = 0 (inactivation at reaction completion). One-step inhibition: v<sub>i</sub> = v<sup>ctrl</sup> (noncovalent complex is not significant at non-saturating inhibitor concentrations). v<sub>t′</sub> = preincubation time–dependent enzyme activity (in AU/s). v<sub>i</sub> = Enzyme activity based without preincubation (in AU/s). v<sub>s</sub> = Enzyme activity after preincubation (t′ > 5t½) based on reaching reaction completion (in AU/s). t′ = preincubation time of enzyme and inhibitor before substrate addition (in s). k<sub>obs</sub> = observed rate of time-dependent inhibition from initial v<sub>i</sub> to final v<sub>s</sub> (in s<sup>−1</sup>).](https://static.yanyin.tech/literature_test/cpz1419-fig-0014-m.jpg)
Algebraic analysis by linear regression to obtain k obs from the (initial) linear slope of LN(enzyme activity) against preincubation time t′ is still frequently reported. This is probably because linear regression is part of benchmark protocols (Ito et al., 1998; Kitz & Wilson, 1962) for kinetic analysis of preincubation time–dependent enzyme inactivation. It is important to note that these benchmark protocols were published before dedicated data analysis software for nonlinear regression was available (Perrin, 2017). Visualization of this ‘linear’ relationship is possible by plotting the enzyme activity against preincubation time t′ on a semilog scale (illustrated in Fig. S1 in Supporting Information).
Preincubation assays are generally disfavored because their experimental execution requires more material and is more laborious than substrate competition assays with continuous read-out (Method I and II). Here, substrate has to be added after the indicated preincubation time, thus requiring multiple individual measurements for each inhibitor concentration. However, preincubation experiments are still favored when reaction completion is too slow for detection during the normal time course of an substrate competition assay (t << t½ in Method I): substrate competition reduces the (covalent) reaction rate and inhibitor solubility limits the maximum inhibitor concentration. Instead, preincubation is performed in the absence of competing substrate, thus reaching the maximum reaction rate at a low inhibitor concentration. Therefore, preincubation experiments are frequently conducted for compounds that display one-step irreversible inhibition behavior because they have a poor noncovalent affinity, such as covalent fragments (Kathman & Statsyuk, 2019). Additionally, preincubation times can exceed the maximum incubation time of progress curve analysis, which is limited by linear product formation ([P]t > 0.1[S]0), as the onset of product formation does not start until preincubation is completed.
This method is less suitable for enzymatic assays with a relatively slow uninhibited product formation velocity vctrl, as assay sensitivity might be insufficient to produce enough product signal F t during a short incubation time. Reaction completion (t′ > 5t½) and/or full inhibition (vt′ = 0) should not be reached before the first (shortest) preincubation time because it will be impossible to detect time-dependent changes in enzyme activity. This can be resolved by increasing the measurement interval (shorter dt′), reduction of the inhibitor concentration, or selection of a different experimental protocol. This method is compatible with two-step irreversible inhibition (Data Analysis 3A) and one-step irreversible inhibition (Data Analysis 3B), but also with (two-step) reversible inhibition (Data Analysis 3C).
The protocol below provides a generic set of steps to accomplishing this type of measurement. Specific reagents, and assay conditions for preincubation time–dependent inhibition of irreversible covalent papain inhibitor fragments can be found in this reference (Kathman et al., 2014).
Materials
1× Assay/reaction buffer supplemented with co-factors and reducing agent Active enzyme, 2× solution in assay buffer Substrate with continuous or quenched read-out, 11× solution in assay buffer Positive control: vehicle/solvent as DMSO stock, or 2% solution in assay buffer Negative control: known inhibitor or alkylating agent as DMSO stock, or 2× solution in assay buffer Inhibitor: as DMSO stock, or serial dilution of 2× solution in assay buffer with 2% DMSO Optional: Development/quenching solution 1.5 ml (Eppendorf) microtubes to prepare stock solutions 384-well low volume microplate with nonbinding surface (e.g., Corning 3820 or 4513) for preincubation and/or read-out General microplate cover/lid (e.g., Corning 6569 Microplate Aluminum Sealing Tape) if preincubation is conducted in a microplate Optional: 96-well microplate to prepare serial dilution of inhibitor concentration Optional: Microtubes to perform preincubations (e.g., Eppendorf Protein Lobind Microtubes, #022431018) Microplate reader equipped with appropriate filters to detect product formation (e.g., CLARIOstar microplate reader) Optional: Automated (acoustic) dispenser (e.g., Labcyte ECHO 550 Liquid Handler acoustic dispenser)
Basic Protocol 8: Preincubation Time–Dependent Inhibition Without Dilution
Before you start , optimize assay conditions in the uninhibited control to ensure compliance with assumptions and restrictions, as outlined in the Critical Parameters: Assumptions on Experimental Assay Conditions section and Basic Protocol I. Consult Table 3 in the troubleshooting section for common optimization and troubleshooting options. Specific adjustments for Method III are that substrate concentration should be relatively low ([S]0 << KM) to minimize disruption of the noncovalent E + I <-> EI equilibrium or reduction of reaction rates by competition (Fig. 14A); adjustment of the enzyme concentration might be required to ensure that maximum 10% of the substrate is processed during the read-out ([P]t < 0.1[S]0) and product formation is linear in the uninhibited control. Furthermore, incubation time t must be relatively short to minimize additional time-dependent enzyme inhibition after substrate addition. As a rule of thumb, incubation must be much shorter than the shortest preincubation (t << t′), unless the product formation read-out is continuous (more details in Data Analysis 3 , step 3). Validate that enough product is formed for a good signal/noise ratio (Z′ > 0.5) by calculating the Z′-score from the uninhibited and inhibited controls (ideally 8 replicates) in a separate experiment (Zhang et al., 1999). This method is compatible with homogeneous (continuous) assays but also with assays that require a development/quenching step to visualize formed product. Note that this protocol was designed for preincubation and read-out in a 384-well microplate.
1.Add inhibitor or control (e.g., 0.2 µl) and assay buffer (e.g., 10 µl) to each well with the uninhibited control for full enzyme activity containing the same volume vehicle/solvent instead of inhibitor as outlined in step 1 of Basic Protocol I.
Gently shake to mix DMSO with the aqueous buffer. Typically, measurements are performed in triplicate (or more replicates) with at least 8 inhibitor concentrations for at least 5 preincubation times. Inhibitor concentrations might need optimization, but a rational starting point is to use inhibitor concentrations below 5 times the IC50 at the shortest preincubation time t′: inhibition is expected to improve in a time-dependent manner and the best results are obtained when full inhibition is not achieved already at the shortest preincubation time (Fig. 14C). Alternatively, larger-volume preincubations (e.g., >200 µl) can be performed in (Eppendorf) microtubes from which aliquots (e.g., 20.2 µl) are transferred to a microplate after the indicated preincubation time. Whether preincubation is performed in a tube or microplate is a matter of personal preference, compatibility with lab equipment and automation, and convenience of dispensing small volumes.
2.Add active enzyme in assay buffer to each well (e.g., 10 µl of 2× solution) or tube to start preincubation of enzyme with inhibitor and homogenize the solution by gently shaking (1 min at 300 rpm). Alternatively, dispensing the enzyme at a high flow rate will also mix the components.
The order of enzyme and inhibitor addition is not important per se , as long as DMSO stocks are added prior to buffered (aqueous) solutions. Inhibitor must be present in excess during preincubation ([I]0 > 10[E]0). Optionally, gently centrifuge the plate or microtubes (1 min at 1000 rpm) to ensure assay components are not stuck at the top of the well.
3.Seal the wells with a cover or lid, and close the caps of microtubes to prevent evaporation of assay components during preincubation.
4.Optional : Transfer aliquots (e.g., 20.2 µl) from the reaction mixture to the microplate after completion of preincubation if performed in larger volumes.
5.Add substrate in assay buffer (e.g., 2 µl of 11× solution) to (at least) three designated replicates after preincubation time t′.
Typically, preincubation can run anywhere from several minutes to hours depending on the enzyme stability and anticipated inhibitor potency, with superior accuracy if the preincubation time is monitored precisely. Substrate should be added in a negligible volume (Vsub < 0.1Vt′) to minimize disruption of the noncovalent equilibria by dilution (Vt = Vt′) (Fig. 14A). Because at steady-state the equilibrium can be disrupted by dilution in too much competitive substrate, keep the substrate volume Vsub and substrate concentration low ([S]0 < 0.1KM) for successful analysis of two-step reversible inhibitors (Data Analysis 3C). Optionally, homogenize the solutions by gentle shaking (300 rpm) and centrifuge the plate or microtubes (1 min at 1000 rpm) to ensure that assay components are not stuck at the top of the well.
6.Quenching : Add development solution to the reaction mixture in the microplate to quench the product formation reaction if read-out of product formation requires a development/quenching step to visualize formed product after incubation time t.
Follow manufacturer's advice on waiting time after addition of development solution before read-out. Incubation time t is the elapsed time between onset of product formation by substrate addition (step 5) and addition of development/quenching solution (step 6). A possible advantage to the use of a quenched assay is the possibility to store the samples after addition of quenching/development solution (step 6) and measure product formation (step 7) in all samples after completion of the final preincubation rather than performing multiple separate measurements (after each preincubation time).
7.Measure formed product after incubation by detection of the product read-out in microplate reader.
Incubation time (after substrate addition) is relatively short (t << LN(2)/k obs) to minimize additional (time-dependent) inhibition of enzyme activity during incubation (Fig. 14B).
8.Repeat Basic Protocol III , steps 4-7 for at least another four preincubation times.
Preincubation time t′ is the elapsed time between onset of inhibition by mixing enzyme and inhibitor (step 2) and addition of substrate (step 5). A typical preincubation assay consists of multiple hours of measuring enzyme activity every 5-30 min, depending on enzyme stability and inhibitor reaction rates. Best results are obtained if the incubation time t used to calculate enzyme activity is kept constant at all preincubation times.
9.Proceed to Basic Data Analysis Protocol 3 to convert the raw experimental data into preincubation time–dependent enzyme activity.
Basic Protocol 9: Preincubation Time–Dependent Inhibition Without Dilution
Processing of raw experimental data obtained with Basic Protocol III for all inhibitor binding modes illustrated in Figure 1.
1.Plot signal F against incubation time t.
Plot signal F (in AU) on the Y-axis against the incubation time (in s) on the X-axis for each inhibitor concentration and for the controls (Fig. 14B). Do this separately for each preincubation time. Proceed to step 3 of this protocol for continuous read-out assays that require a longer incubation time to produce enough product for a good signal/noise ratio.
2.Fit F t against t to obtain vt′.
Fit signal F (in AU) against incubation time t (in s) to Equation XIII (Fig. 15B/Fig. 16B, left) to obtain preincubation time–dependent product formation velocity vt′ (in AU/s) from the linear slope. Consult Table 3 for troubleshooting if product formation is not linear.
\begin{equation} {F_{\rm {t}}} = {F_0} + {{\rm{v}}_{\rm{t^\prime}}}t \end{equation}
Equation XIII for nonlinear regression of straight line Y = YIntercept + Slope*X with Y = signal F t (in AU) and X = incubation time t (in s) to find YIntercept = background signal at reaction initiation F 0 (in AU) and Slope = preincubation time–dependent product formation velocity vt′ (in AU/s).
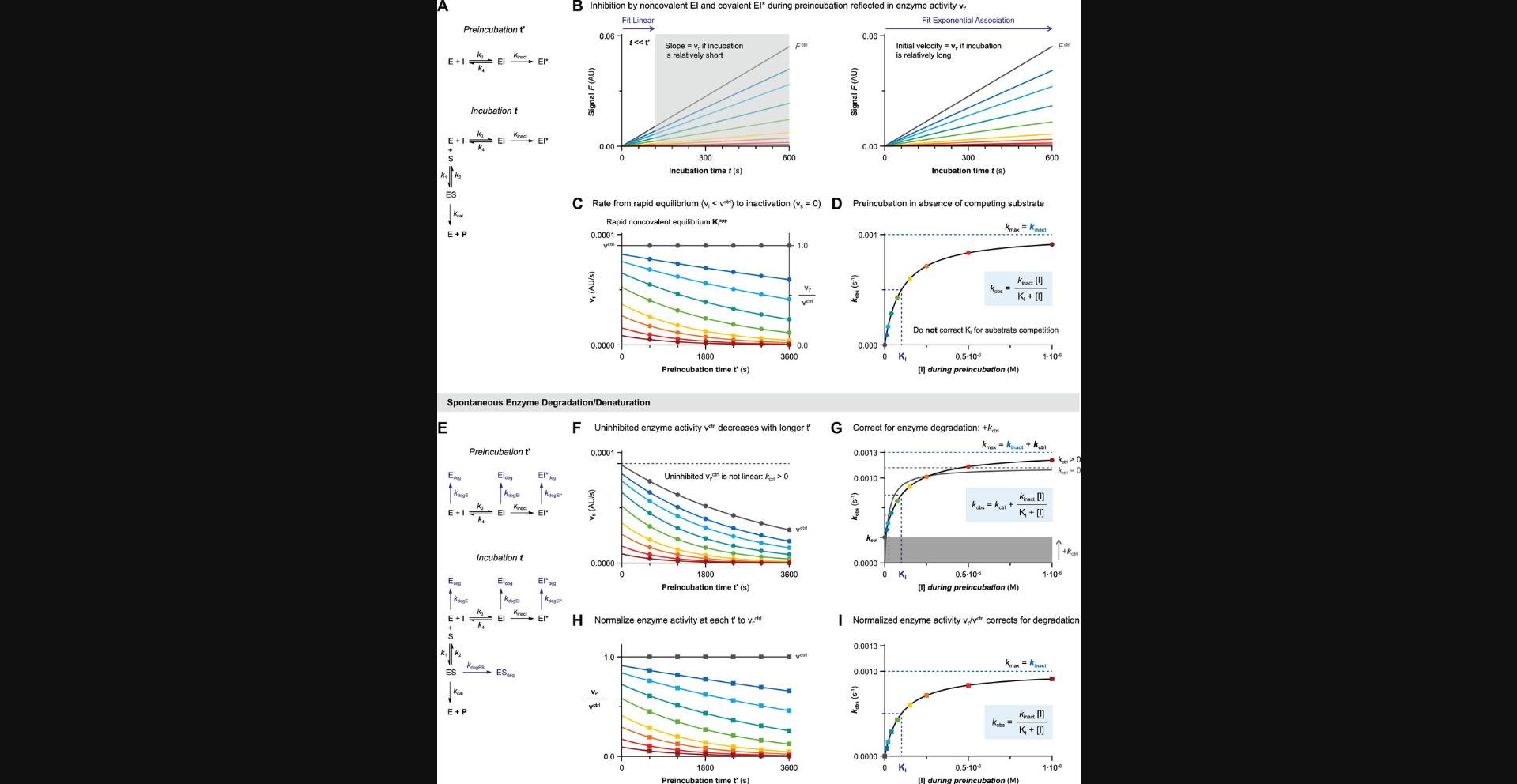
![Details are in the caption following the image Data Analysis 3B: Preincubation time–dependent inhibition without dilution for one-step irreversible covalent inhibition. Simulated with KinGen (A-D) or KinDeg (E-I) for inhibitor D with 1 pM enzyme and 100 nM substrate S1. (A) Schematic enzyme dynamics during preincubation in absence of substrate and during incubation after substrate addition for one-step irreversible covalent inhibition. (B) Time-dependent product formation after preincubation in absence of inhibitor F<sup>ctrl</sup> or in presence of inhibitor (t′ = 1800 s). Left: Enzyme activity after preincubation v<sub>t′</sub> is obtained from the linear slope if the incubation time is relatively short (t << t′): gray area is excluded from the fit. Right: Enzyme activity after preincubation v<sub>t′</sub> is obtained from the initial velocity of the exponential association progress curve of each inhibitor concentration. (C) Preincubation time–dependent enzyme activity v<sub>t′</sub> is fitted to Equation V (Fig. 14D) (constraining v<sub>s</sub> = 0) for each inhibitor concentration to obtain observed rates of inactivation k<sub>obs</sub>. v<sub>i</sub> = v<sup>ctrl</sup> for one-step irreversible inhibitors and two-step irreversible inhibitors at non-saturating concentrations ([I] << K<sub>i</sub><sup>app</sup>). Alternatively, v<sub>t′</sub> can be normalized to a fraction of the uninhibited enzyme activity v<sup>ctrl</sup>. (D) Inhibitor concentration–dependent k<sub>obs</sub> increases linearly with inhibitor concentration, with k<sub>chem</sub> as the slope. No correction for substrate competition because v<sub>t′</sub> reflects the enzyme activity after preincubation in absence of competing substrate. (E) Schematic enzyme dynamics during preincubation in absence of substrate and during incubation after substrate addition for one-step irreversible covalent inhibition with spontaneous enzyme degradation/denaturation. Simulated with k<sub>degE</sub> = k<sub>degES</sub> = k<sub>degEI*</sub> = 0.0003 s<sup>−1</sup>. (F) Uninhibited enzyme activity after preincubation v<sub>t′</sub><sup>ctrl</sup> is not linear: k<sub>ctrl</sub> > 0. Preincubation time–dependent enzyme activity v<sub>t′</sub> is fitted to Equation V (Fig. 14D) (constraining v<sub>s</sub> = 0 and shared value for v<sub>i</sub> = uninhibited enzyme activity without preincubation v<sub>0</sub><sup>ctrl</sup>) for each inhibitor concentration to obtain observed rates of inactivation k<sub>obs</sub>, as well as fitting uninhibited activity v<sub>t′</sub><sup>ctrl</sup> to obtain the rate of nonlinearity k<sub>ctrl</sub>. (G) Inhibitor concentration–dependent k<sub>obs</sub> with spontaneous enzyme degradation/denaturation increases by k<sub>ctrl</sub>. Fit with algebraic correction for nonlinearity (black line, k<sub>ctrl</sub> > 0) or ignoring nonlinearity (gray line, constrain k<sub>ctrl</sub> = 0). Ignoring the nonlinearity (assuming Y-intercept = 0) results in overestimation of k<sub>chem</sub> (steeper slope). (H) Normalized enzyme activity v<sub>t′</sub>/v<sup>ctrl</sup> is fitted to Equation V (Fig. 14D) (constraining v<sub>s</sub> = 0 and Y-intercept = v<sub>i</sub>/v<sub>0</sub><sup>ctrl</sup> = 1) for each inhibitor concentration to obtain corrected observed rates of inactivation k<sub>obs</sub>. (I) Inhibitor concentration-dependent k<sub>obs</sub> has been corrected for enzyme degradation/denaturation by fitting normalized enzyme activity v<sub>t′</sub>/v<sup>ctrl</sup> and does not require further corrections.](https://static.yanyin.tech/literature_test/cpz1419-fig-0016-m.jpg)
3.A lternative for continuous : Fit F t against t to obtain vt′.
This is an alternative method to obtain vt′ from the initial velocity for assays with a continuous readout, using the initial velocity in progress curve analysis (Method I). Fit signal F t against incubation time t to exponential association Equation XIV (Fig. 15B/Fig. 16B, right) to obtain preincubation time–dependent product formation velocity vt′ (in AU/s) from the initial velocity. This resolves issues with low signal/noise ratios for continuous read-out assays where vt′ is not linear (due to additional covalent modification during the incubation) by allowing longer incubation times to produce sufficient signal.
\begin{equation} {F_{\rm {t}}} = ;{{\rm{v}}{\rm{s}}}t + \frac{{{{\rm{v}}{\rm{t^\prime}}} - {{\rm{v}}_{\rm{s}}}}}{k}\left[ {1 - {e^{ - kt}}} \right] + {F_0} \end{equation}
Equation XIV for nonlinear regression of user-defined explicit equation Y = (vsX) + (((vi-vs)/kobs)(1-EXP(-kobs*X))) + Y0 with Y = signal F t (in AU) and X = incubation time t (in s) to find Y0 = Y-intercept F 0 = background signal at t = 0 (in AU), vi = initial slope = preincubation time–dependent product formation velocity vt′ (in AU/s), vs = final slope (in AU/s) and kobs = nonlinearity reaction rate k (in s−1).
4.Proceed to Data Analysis Protocols to obtain the appropriate kinetic parameters for each covalent binding mode: Data Analysis Protocol 3Ai or 3Aii for two-step irreversible inhibitors, Data Analysis Protocol 3Bi or 3Bii for one-step irreversible inhibitors, and Basic Data Analysis Protocol 3C for two-step reversible inhibitors.
Selection of a data analysis method for inhibitors with an irreversible binding mode depends on the desired visual representation as well as personal preference. Generally, Basic Data Analysis Protocols 3Ai and 3Bi have less data processing/manipulation and are more informative for comparison of various inhibitors on a single enzyme target, as they are compatible with assessment of inhibitor potency simultaneous with visual assessment of time-dependent enzyme stability k ctrl (Figs. 15F and 16F). Alternative Data Analysis Protocols 3Aii and 3Bii involve normalization of the enzyme activity that aids visual assessment of inhibitory potency of a single inhibitor on multiple enzyme targets (that might have a variable stability) (Figs. 15H and 16H).
| Data Analysis Protocol | |||
|---|---|---|---|
| EXP Conditions | 2-step IRREV | 1-step IRREV | 2-step REV |
| kctrl = 0 | 3Ai | 3B | 3C |
| kdegE = 0 | 3Ai/3Aii | 3Bi/3Bii | 3C |
Exemplary assay concentrations during preincubation and during incubation.
| Concentration during preincubation t′ | Concentration during incubation t | |||||
|---|---|---|---|---|---|---|
| [stock] | V (µl) | [conc]t′ | [stock] | V (µl) | [conc]t | |
| Enzyme | 2 nM | 10 | 0.99 nM | - | - | 0.90 nM |
| Inhibitor | 20 nM | 10.2 | 10.10 nM | - | - | 9.19 nM |
| Substrate | - | - | - | 11 µM | 2 | 0.99 µM |
| Total | 20.2 | 22.2 | ||||
Data Analysis 3A: Preincubation Time–Dependent Inhibition Without Dilution for Two-Step Irreversible Covalent Inhibition
Time-dependent product formation is fitted to a straight line for each inhibitor concentration to obtain the enzyme activity after preincubation vt′ (in AU/s) from the linear (initial) slope (Fig. 15A and 15B, left). It is important that the incubation time be relatively short (t < 0.1t½) to minimize artifacts caused by significant formation of covalent adduct EI* after substrate addition (ΔEI*) because vt′ should reflect the enzyme activity at the end of preincubation. As a rule of thumb, incubation time t should be much shorter than the shortest preincubation time t′. A short incubation time may result in insufficient product formation for a robust signal, which can be resolved by increasing the incubation time and obtaining enzyme activity vt′ from the initial velocity of the exponential association progress curve, provided that the assay is compatible with progress curve analysis (continuous read-out) (Fig. 15B, right). Enzyme activity after preincubation vt′ is fitted to bounded exponential decay Equation V (Fig. 14D) (constraining vs = 0) for each inhibitor concentration to obtain the observed rate of reaction completion k obs from enzyme activity without preincubation (Y-intercept at vi) to reaching the final enzyme inactivation (plateau at vs = 0) (Fig. 15C). Enzyme activity without preincubation in presence of inhibitor vi is lower than the uninhibited enzyme activity vctrl for two-step (ir)reversible inhibitors, because vi reflects the rapid noncovalent equilibrium (Kiapp) after substrate addition (Copeland, 2013b). The plot of inhibitor concentration-dependent k obs reaches maximum rate of inactivation k inact in presence of saturating inhibitor concentration ([I] >> KI) with the Y-intercept at k ctrl = 0 when uninhibited enzyme activity vctrl is independent of preincubation time (Fig. 15D). Inhibitor concentrations should correspond with the inhibitor concentration during preincubation (rather than after substrate addition). Correction of inactivation constant KI for substrate competition is not necessary because preincubation is performed in absence of substrate.
Warnings and Remarks
The rapid noncovalent E + I <-> EI equilibrium does not significantly contribute to inhibition at non-saturating inhibitor concentrations ([I] << Kiapp), resulting in one-step binding behavior (Fig. 3F). This will be apparent from the observation that initial velocity vi is independent of inhibitor concentration (vi = vctrl) along with a linear plot of k obs against [I]. This is resolved either by increasing the inhibitor concentration or performing Data Analysis 3B. Increasing the substrate concentration can resolve issues with assay sensitivity associated with short incubation times, as this will result in a higher product signal. However, substrate addition in a relatively large volume (Vsub > 0.1Vt′) and/or addition of a competitive substrate concentration ([S] > 0.1KM) causes (partial) disruption of the reversible equilibrium, although this does not affect the accuracy of k obs for irreversible inhibitors. In fact, disruption of the noncovalent complex can be employed to detect covalent adduct formation of two-step irreversible inhibitors that exhibit tight-binding behavior (Copeland, 2013c; Murphy, 2004) resulting from very potent noncovalent inhibition, as will be discussed in Method IV.
Uninhibited enzyme activity vctrl decreases when preincubation is long enough for significant spontaneous enzyme degradation (t′ >> 0.1t½) (Fig. 15F). A simple algebraic correction for spontaneous enzyme degradation results in good estimates for k inact and KI if all enzyme species have the same first-order enzymatic degradation rate (k degE = k degES = k degEI) (Fig. 15G). Alternatively, normalizing the enzyme activity vt′ to uninhibited enzyme activity vt′ctrl at each preincubation time corrects for enzyme degradation (Fig. 15H), and k obs obtained from normalized enzyme activity vt′/vctrl results in good estimates of k inact and KI without further correction (Fig. 15I).
Basic Protocol 10: Two-Step Irreversible Covalent Inhibition
Processing of experimental data obtained with Basic Protocol III that has been processed according to Basic Data Analysis Protocol 3 for two-step irreversible covalent inhibitors.
1.Plot vt′ against preincubation time t′ for each inhibitor concentration.
Plot the mean and standard deviation of vt′ (in AU/s) on the Y-axis against preincubation time t′ (in s) on the X-axis for each inhibitor concentration and the uninhibited control (Fig. 14C/Fig. 15C). Validate that inhibitor concentrations are not too high: inhibition should be less than 100% at the shortest t′ for at least six inhibitor concentrations. Check whether the uninhibited enzyme activity is independent of preincubation time (v0ctrl = vt′ctrl, Fig. 15C): an algebraic correction for enzyme instability (k ctrl > 0, Fig. 15F) can be performed in step 4 of this protocol by accounting for nonlinearity in the uninhibited control in the secondary k obs plot (Fig. 15G). Alternatively, proceed to Alternative Data Analysis Protocol 3Aii to correct for enzyme instability (v0ctrl > vt′ctrl) by normalization of the enzyme activity vt′/vt′ctrl (Fig. 15H-I).
2.Fit vt′ against preincubation time t′ to obtain k obs.
Fit the mean and standard deviation of vt′ against preincubation time t′ (Fig. 15C/F) to Equation V. Constrain vs = value in fully inhibited control to obtain the observed reaction rate k obs (in s−1) from initial velocity vi (Y-intercept) to full inactivation (Plateau = 0). A lack of initial noncovalent complex (vi = v0ctrl) is indicative of one-step binding behavior.
\begin{equation} {{\rm{v}}{{\rm{t^\prime}}}} = {{\rm{v}}{\rm{s}}} + ({\rm{v_i}} - {{\rm{v}}{\rm{s}}});{e^{ - {k{{\rm{obs}}}}\rm t^\prime}} \end{equation}
Equation V for nonlinear regression of exponential one-phase decay equation Y = (Y0-Plateau)EXP(-kX) + Plateau with Y = preincubation time–dependent product formation velocity vt′ (in AU/s), X = preincubation time t′ (in s), and Plateau = final velocity in the fully inhibited control vs (in AU/s) to find Y0 = Y-intercept = initial velocity vi (in AU/s) and k = observed reaction rate k obs (in s−1).
3.Plot k obs against [I].
Plot the mean and standard deviation of k obs (in s−1) on the Y-axis against inhibitor concentration (in M) during preincubation (before addition of substrate) on the X-axis (Fig. 15D/G). The plot of k obs against [I] should reach a maximum k obs at saturating inhibitor concentration. Note that a linear curve is indicative of one-step binding behavior at non-saturating inhibitor concentrations ([I] << 0.1KI in Fig. 3F) with vi = v0ctrl (shared Y-intercept in the previous step). Proceed to Basic Data Analysis Protocol 3Bi step 4 after it has been validated that the linear curve is not resultant from saturating inhibitor concentrations ([I] >> 10KI in Fig. 3G) as identified by vi << v0ctrl, by repeating the measurement with lower inhibitor concentrations.
4.Fit k obs against [I] to obtain k inact and KI.
Fit k obs (in s−1) against inhibitor concentration during preincubation (in M) to Equation XV to obtain maximum inactivation rate constant k inact (in s−1) and inactivation constant KI (in M). Constrain k ctrl = k obs of the uninhibited control (Fig. 15G). Inactivation constant KI does not have to be corrected for substrate competition because preincubation is conducted in absence of competing substrate. Calculate irreversible covalent inhibitor potency k inact/KI (in M−1s−1) with propagation of error with Sample Calculation 2.
\begin{equation} {k_{{\rm{obs}}}} = {k_{{\rm{ctrl}}}} + \frac{{{k_{{\rm{inact}}}}{\rm{;}}\left[ {\rm{I}} \right]}}{{{{\rm{K}}_{\rm{I}}} + \left[ {\rm{I}} \right]}};; \end{equation}
Equation XV for nonlinear regression of user-defined explicit equation Y = Y0 + ((kmax*X)/((KI) + X)) with Y = observed reaction rate k obs (in s−1) and X = inhibitor concentration during preincubation (in M) to find Y0 = rate of nonlinearity in uninhibited control k ctrl (in s−1), kmax = maximum reaction rate k inact (in s−1) and KI = Inactivation constant KI (in M).
5.Optional : Validate experimental kinetic parameters with kinetic simulations.
Proceed to Kinetic Simulations 1 to compare the experimental read-out to the product formation simulated with scripts KinGen and KinDeg (using experimental rate constant k inact = k 5) to confirm that the calculated kinetic constants are in accordance with the experimental data. Also perform simulations with KinVol and KinVolDeg to confirm that addition of substrate does not significantly affect the noncovalent interactions.
Basic Protocol 11: Two-Step Irreversible Covalent Inhibition
Processing of experimental data obtained with Basic Protocol III that has been processed according to Basic Data Analysis Protocol 3 for two-step irreversible covalent inhibitors.
1.Plot vt′ against preincubation time t′ for each inhibitor concentration.
Plot the mean and standard deviation of vt′ (in AU/s) on the Y-axis against preincubation time t′ (in s) on the X-axis for each inhibitor concentration and the uninhibited control (Fig. 14C/Fig. 15C). Validate that inhibitor concentrations are not too high: inhibition should be less than 100% at the shortest t′ for at least six inhibitor concentrations.
2.Normalize vt′ to obtain vt′/vctrl.
Normalize vt′ (in AU/s) of each inhibitor concentration and the controls to lowest value = 0 (or full inhibition control) and highest value = uninhibited product formation vt′ctrl (in AU/s) to obtain normalized enzyme activity vt′/vctrl (Fig. 15H). Perform this correction separately for each preincubation time.
3.Plot and fit vt′/vctrl against preincubation time t′ to obtain k obs.
Plot the mean and standard deviation of vt′/vctrl on the Y-axis against preincubation time t′ (in s) on the X-axis (Fig. 15H). Fit to exponential decay Equation XVI to obtain k obs (in s−1) from initial velocity vi/v0ctrl to full inactivation (Plateau = 0). A lack of initial noncovalent complex (vi/v0ctrl = 1) is indicative of one-step binding behavior.
\begin{equation} \left( {\frac{{{\rm v_{t^\prime }}}}{{\rm v_{t^\prime }^{{\rm{ctrl}}}}}} \right) = \left( {\frac{{{\rm v_i}}}{{\rm v_0^{{\rm{ctrl}}}}}} \right){e^{ - {k_{{\rm{obs}}}}\rm t^\prime}} \end{equation}
Equation XVI for nonlinear regression of exponential one-phase decay equation Y = (Y0-Plateau)EXP(-kX) + Plateau with Y = normalized preincubation time–dependent product formation velocity vt′/vctrl (unitless), X = preincubation time t′ (in s), and Plateau = normalized final velocity vs/vsctrl = 0 (unitless) to find Y0 = Y-intercept = normalized initial velocity vi/v0ctrl (unitless) and k = observed reaction rate k obs (in s−1).
4.Plot k obs against [I].
Plot the mean and standard deviation of k obs (in s−1) on the Y-axis against inhibitor concentration (in M) during preincubation (before addition of substrate) on the X-axis (Fig. 15I). The plot of k obs against [I] should have a Y-intercept = 0, and reach a maximum k obs at saturating inhibitor concentration. Note that a linear curve is indicative of one-step binding behavior at non-saturating inhibitor concentrations ([I] << 0.1KI in Fig. 3F) with vi = v0ctrl (shared Y-intercept = 1 in the previous step). Proceed to Basic Data Analysis Protocol 3Bii step 5 after it has been validated that the linear curve is not resultant from saturating inhibitor concentrations ([I] >> 10KI in Fig. 3G) as identified by vi << v0ctrl (shared Y-intercept = 0 in the previous step), by repeating the measurement with lower inhibitor concentrations.
5.Fit k obs against [I] to obtain k inact and KI.
Fit k obs against inhibitor concentration during preincubation to Equation XVII to obtain maximum inactivation rate constant k inact (in s−1) and inactivation constant KI (in M) (Fig. 15I). Do not correct for enzyme instability (k ctrl > 0), as this correction has already been performed by normalizing vt′ to vt′/vctrl in step 2 of this protocol. Inactivation constant KI does not have to be corrected for substrate competition because preincubation is conducted in absence of competing substrate. Calculate irreversible covalent inhibitor potency k inact/KI (in M−1s−1) with propagation of error with Sample Calculation 2.
\begin{equation} {k_{{\rm{obs}}}} = \frac{{{k_{{\rm{inact}}}}{\rm{;}}\left[ {\rm{I}} \right]}}{{{{\rm{K}}_{\rm{I}}} + \left[ {\rm{I}} \right]}};; \end{equation}
Equation XVII for nonlinear regression of user-defined explicit equation Y = Y0 + ((kmax*X)/((KI) + X)) with Y = observed reaction rate k obs (in s−1), X = inhibitor concentration during preincubation (in M) and Y0 = 0 (in s−1) to find kmax = maximum reaction rate k inact (in s−1) and KI = Inactivation constant KI (in M).
6.Optional : Validate experimental kinetic parameters with kinetic simulations by proceeding to Basic Data Analysis Protocol 3Ai , step 5.
Data Analysis 3B: Preincubation Time–Dependent Inhibition Without Dilution for One-Step Irreversible Covalent Inhibition
Time-dependent product formation is fitted to a straight line for each inhibitor concentration to obtain the enzyme activity after preincubation vt′ (in AU/s) from the linear slope (Fig. 16A and 16B, left). Incubation must be short enough to minimize formation of covalent adduct EI* after substrate addition (t << t½); otherwise k chem will be overestimated. Similar to Data Analysis 3A , preincubation-dependent enzyme activity vt′ can also be obtained from the initial velocity of the exponential association progress curve, provided that the read-out is continuous (Fig. 16B, right). Enzyme activity after preincubation vt′ is fitted to bounded exponential decay Equation V (Fig. 14D) to obtain observed rate of reaction completion k obs from uninhibited enzyme activity without preincubation (Y-intercept at vi = vctrl) to reaching the final enzyme inactivation (constraining vs = 0) (Fig. 16C). Inhibited enzyme activity without preincubation is equal to uninhibited enzyme activity (vi = vctrl), as rapid noncovalent inhibitor binding does not contribute to enzyme inhibition by one-step irreversible inhibitors. The slope of the linear plot of k obs against inhibitor concentration during preincubation is equal to k chem (Fig. 16D), which should not be corrected for substrate competition as preincubation is performed in absence of competing substrate.
Warnings and remarks
Substrate addition in a relatively large volume (Vsub > 0.1Vt′) and/or addition of a competitive substrate concentration ([S] > 0.1KM) does not significantly affect the accuracy of k obs because one-step irreversible inhibition does not involve a rapid noncovalent equilibrium that can be disrupted (also see Method IV). Increasing the substrate concentration can resolve issues with assay sensitivity: higher substrate concentration results in a higher product concentration after the same incubation time (vctrl = V max[S]/([S]+KM)), which in turn will result in a better signal to noise ratio.
Uninhibited enzyme activity vctrl decreases with longer preincubation due to spontaneous enzyme degradation (Fig. 16E and 16F). This especially affects assays where preincubation is long enough for significant enzyme degradation (t′ > 0.1t½). Algebraic correction for spontaneous enzyme degradation (k degE = k degES) in the secondary k obs plot is relatively simple (Fig. 16G). Alternatively, correction for enzyme degradation is performed by normalizing enzyme activity vt′ to uninhibited enzyme activity vt′ctrl at each preincubation time (Fig. 16H and 16I). Stabilization of enzyme upon inhibitor binding (k degEI* < k degE) does not affect k obs, as EI* formation is already irreversible thus removing the species from the available pool of catalytic enzyme.
Basic Protocol 12: One-Step Irreversible Covalent Inhibition
Processing of experimental data obtained with Basic Protocol III that has been processed according to Basic Data Analysis Protocol 3 for one-step irreversible covalent inhibitors and two-step irreversible inhibitors at non-saturating inhibitor concentrations ([I] ≤ 0.1KI).
1.Plot vt′ against preincubation time t′ for each inhibitor concentration.
Plot the mean and standard deviation of vt′ (in AU/s) on the Y-axis against preincubation time t′ (in s) on the X-axis for each inhibitor concentration and the uninhibited control (Fig. 14C/Fig. 16C). Validate that inhibitor concentrations are not too high: inhibition should be less than 100% at the shortest t′ for at least six inhibitor concentrations. Check whether the uninhibited enzyme activity is independent of preincubation time (v0ctrl = vt′ctrl, Fig. 16C): an algebraic correction for enzyme instability (k ctrl > 0, Fig. 16F) can be performed in step 4 of this protocol by accounting for nonlinearity in the uninhibited control in the secondary k obs plot (Fig. 16G). Alternatively, proceed to Alternative Data Analysis Protocol 3Bii to correct for enzyme instability (v0ctrl > vt′ctrl) by normalization of the enzyme activity vt′/vt′ctrl (Fig. 16H-I).
2.Fit vt′ against preincubation time t′ to obtain k obs.
Fit the mean and standard deviation of vt′ against preincubation time t′ (Fig. 16C/F) to Equation V. Constrain vs = value in fully inhibited control to obtain the observed reaction rate k obs (in s−1) from initial velocity vi (Y-intercept) to full inactivation (Plateau = 0). A lack of initial noncovalent complex (vi = v0ctrl) is indicative of one-step binding behavior.
\begin{equation} {{\rm{v}}{{\rm{t^\prime}}}} = {{\rm{v}}{\rm{s}}} + \left( {{{\rm{v}}{\rm{i}}} - {{\rm{v}}{\rm{s}}}} \right);{e^{ - {k_{{\rm{obs}}}}{\rm{t^\prime}} }} \end{equation}
Equation V for nonlinear regression of exponential one-phase decay equation Y = (Y0-Plateau)EXP(-kX) + Plateau with Y = preincubation time–dependent product formation velocity vt′ (in AU/s), X = preincubation time t′ (in s), and Plateau = final velocity in the fully inhibited control vs (in AU/s) to find Y0 = Y-intercept = initial velocity vi = uninhibited initial velocity v0ctrl (in AU/s, shared value) and k = observed reaction rate k obs (in s−1).
3.Plot k obs against [I].
Plot the mean and standard deviation of k obs (in s−1) on the Y-axis against inhibitor concentration (in M) during preincubation (before addition of substrate) on the X-axis (Fig. 16D/G). The plot of k obs against inhibitor concentration [I] is linear for one-step irreversible inhibitors and for two-step irreversible inhibitors at non-saturating inhibitor concentrations ([I] << 0.1KI).
4.Fit k obs against [I] to obtain k chem.
Fit k obs against inhibitor concentration during preincubation (in M) to Equation XVIII to obtain inhibitor potency k chem (in M−1s−1) from the linear slope. Constrain Y-intercept k ctrl = k obs of the uninhibited control (Fig. 16G). Inhibitor potency k chem does not have to be corrected for substrate competition because preincubation is conducted in absence of competing substrate. Calculate k inact/KI (in M−1s−1) for two-step irreversible inhibitors at non-saturating inhibitor concentrations ([I] ≤ 0.1KI) with propagation of error with Sample Calculation 9.
\begin{equation} {k_{{\rm{obs}}}} = {k_{{\rm{ctrl}}}} + {k_{{\rm{chem}}}}\left[ {\rm{I}} \right] \end{equation}
Equation XVIII for nonlinear regression of straight line Y = YIntercept + Slope*X with Y = observed reaction rate k obs (in s−1) and X = inhibitor concentration during preincubation (in M) to find YIntercept = rate of nonlinearity in uninhibited control k ctrl (in s−1) and Slope = inactivation rate constant k chem (in M−1s−1)
5.Optional : Validate experimental kinetic parameters with kinetic simulations.
Proceed to Kinetic Simulations 1 to compare the experimental read-out to the product formation simulated with scripts KinGen and KinDeg (using experimental rate constant k chem = k 3) to confirm that the calculated kinetic constants are in accordance with the experimental data. Also perform simulations with KinVol and KinVolDeg to confirm that addition of substrate does not significantly affect the reaction rates by dilution and/or competition.
Basic Protocol 13: One-Step Irreversible Covalent Inhibition
Processing of experimental data obtained with Basic Protocol III that has been processed according to Basic Data Analysis Protocol 3 for one-step irreversible covalent inhibitors and two-step irreversible inhibitors at non-saturating inhibitor concentrations ([I] ≤ 0.1KI).
1.Plot vt′ against preincubation time t′ for each inhibitor concentration.
Plot the mean and standard deviation of vt′ (in AU/s) on the Y-axis against preincubation time t′ (in s) on the X-axis for each inhibitor concentration and the uninhibited control (Fig. 14C/Fig. 16C). Validate that inhibitor concentrations are not too high: inhibition should be less than 100% at the shortest t′ for at least six inhibitor concentrations.
2.Normalize vt′ to obtain vt′/vctrl.
Normalize vt′ (in AU/s) of each inhibitor concentration and the controls to lowest value = 0 (or full inhibition control) and highest value = uninhibited product formation vt′ctrl (in AU/s) to obtain normalized enzyme activity vt′/vctrl (Fig. 16H). Perform this correction separately for each preincubation time.
3.Plot and fit vt′/vctrl against preincubation time t′ to obtain k obs
Plot the mean and standard deviation of vt′/vctrl on the Y-axis against preincubation time t′ (in s) on the X-axis (Fig. 16H). Fit to exponential decay Equation XVI to obtain k obs (in s−1) from initial velocity vi/v0ctrl to full inactivation (Plateau = 0). A lack of initial noncovalent complex (vi/v0ctrl = 1) is indicative of one-step binding behavior.
\begin{equation} \left( {\frac{{{{\rm{v}}{{\rm{t^\prime}}}}}}{{{\rm{v}}{{\rm{t^\prime}}}^{{\rm{ctrl}}}}}} \right) = {e^{ - {k_{{\rm{obs}}}}{\rm{t^\prime}}}} \end{equation}
Equation XVI for nonlinear regression of exponential one-phase decay equation Y = (Y0-Plateau)EXP(-kX) + Plateau with Y = normalized preincubation time–dependent product formation velocity vt′/vctrl (unitless), X = preincubation time t′ (in s), Y0 = Y-intercept = normalized initial velocity vi/v0ctrl =1 (unitless), and Plateau = normalized final velocity vs/vsctrl = 0 (unitless) to find k = observed reaction rate k obs (in s−1).
4.Plot k obs against [I].
Plot the mean and standard deviation of k obs (in s−1) on the Y-axis against inhibitor concentration (in M) during preincubation (before addition of substrate) on the X-axis (Fig. 16I). The plot of k obs against inhibitor concentration [I] is linear for one-step irreversible inhibitors and for two-step irreversible inhibitors at non-saturating inhibitor concentrations ([I] << 0.1KI).
5.Fit k obs against [I] to obtain k chem.
Fit k obs against inhibitor concentration during preincubation to Equation XIX to inhibitor potency k chem (in M−1s−1) from the linear slope (Fig. 16I). Do not correct for enzyme instability (k ctrl > 0), as this correction has already been performed by normalizing vt′ to vt′/vctrl in step 2 of this protocol. Inhibitor potency k chem does not have to be corrected for substrate competition because preincubation is conducted in absence of competing substrate. Calculate k inact/KI (in M−1s−1) for two-step irreversible inhibitors at non-saturating inhibitor concentrations ([I] ≤ 0.1KI) with propagation of error with Sample Calculation 9. Alternatively, inhibitor potency k chem (in M−1s−1) or k inact/KI (in M−1s−1) can be directly calculated from a single k obs (s−1) and [I] (in M) with Sample Calculation 10.
\begin{equation} {k_{{\rm{obs}}}} = {k_{{\rm{chem}}}}\left[ {\rm{I}} \right] \end{equation}
Equation XIX for nonlinear regression of straight line Y = YIntercept + Slope*X with Y = observed reaction rate k obs (in s−1), X = inhibitor concentration during preincubation (in M), and YIntercept = 0 (in s−1) to find Slope = inactivation rate constant k chem (in M−1s−1).
6.Optional : Validate experimental kinetic parameters with kinetic simulations by proceeding to Basic Data Analysis Protocol 3Bi step 5.
Data Analysis 3C: Preincubation Time–Dependent Inhibition Without Dilution for Reversible Covalent Inhibition
Time-dependent product formation is fitted to a straight line for each inhibitor concentration to obtain the enzyme activity after preincubation vt′ (in AU/s) from the linear slope (Fig. 17A and 17B). Again, it is important that the incubation time be much shorter than the shortest preincubation time t′ (t << t′), but enzyme activity vt′ can also be calculated from the initial velocity of the exponential association progress curve, provided that the assay is compatible with progress curve analysis (continuous read-out). Enzyme activity after preincubation vt′ is fitted to bounded exponential decay Equation V (Fig. 14D) for each inhibitor concentration to obtain observed rate of reaction completion k obs from rapid noncovalent equilibrium (Y-intercept at vi < vctrl) to slowly reaching steady-state equilibrium (plateau at vs > 0) (Fig. 17C). Enzyme activity without preincubation in presence of inhibitor vi is lower than the uninhibited enzyme activity vctrl for two-step (ir)reversible inhibitors because vi reflects the rapid noncovalent equilibrium (Kiapp) after substrate addition (Copeland, 2013b). Contrary to irreversible inhibition, the plateau (vs > 0) does not approximate enzyme inactivation but reaches the steady-state equilibrium (Ki) instead. Steady-state inhibition constant Ki can be calculated from the fitted values of Ki, k 5 and k 6 (Fig. 17D), but this is not the preferred approach as a small error in k 6 has huge implications for the calculation of Ki* (as illustrated in Fig. 9). Generally, more reliable estimates of the steady-state inhibition constant Ki* are generated from the dose-response curve of steady-state velocity vs against inhibitor concentration during preincubation (Fig. 17E).
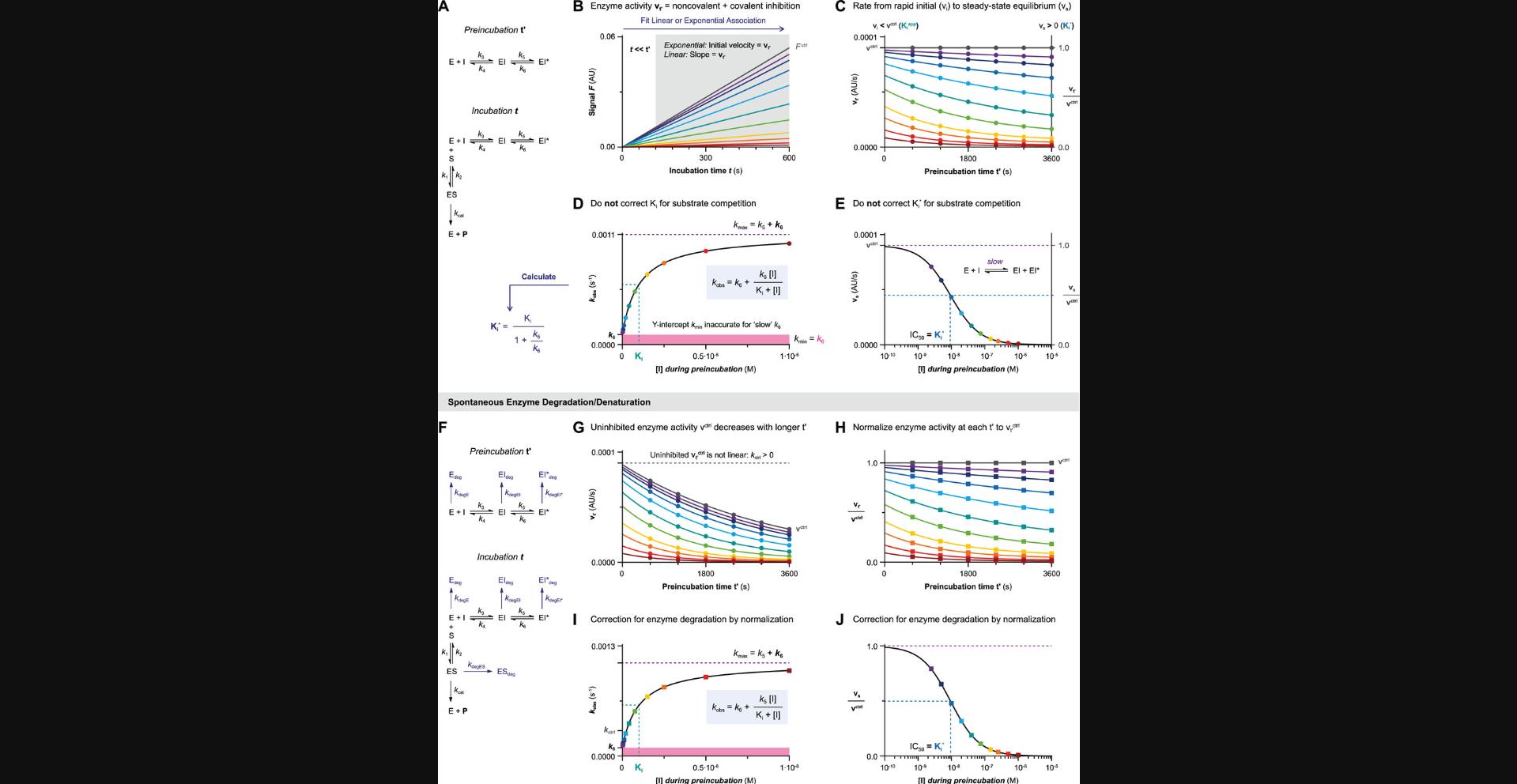
Warnings and remarks
Steady-state inhibition constant Ki* reflects the reversible E + I <-> EI + EI* equilibrium that can be disrupted by substrate addition in a relatively large volume (Vsub > 0.1Vt′) and/or addition of a competitive substrate concentration ([S] > 0.1KM). Simulations with high substrate concentration ([S] = 10KM) show that the IC50 of the dose-response curve for steady-state velocity vs was slightly higher than steady-state inhibition constant Ki*, but still significantly lower than Kiapp, as covalent dissociation will not be significant as long as the incubation time is significantly shorter than the dissociation half-life (t << t½diss). Altogether, fitting exponential association rather than increasing the substrate concentration is the desired solution to resolve issues with assay sensitivity associated with short incubation times. Alternatively, reasonable estimates of the steady-state inhibition constant Ki were obtained from the endpoint preincubation time–dependent potency IC50(t′) with minimal substrate competition ([S] << KM) and preincubation times exceeding the required time to reach reaction completion at all inhibitor concentrations (t′ > 5t½).
As mentioned before, spontaneous loss of enzyme activity due to first-order degradation and/or denaturation of enzyme species (k degE = k degES = k degEI) results in a preincubation time–dependent decrease of uninhibited enzyme activity vctrl (Fig. 17E and 17F). The biggest advantage of Method III over Method I (Data Analysis 1C) is that it is possible to perform an algebraic correction for the enzyme instability in kinetic analysis of two-step reversible covalent inhibitors with Data Analysis 3C. Enzyme activity vt′ is normalized to uninhibited enzyme activity vt′ctrl at each preincubation time (Fig. 17G), and the normalized enzyme activity after preincubation vt′/vctrl is fitted to bounded exponential decay Equation V (Fig. 14D) for each inhibitor concentration to obtain observed rate of reaction completion k obs and steady-state velocity vs. Kinetic analysis of k obs (Fig. 17H) and steady-state velocity vs (Fig. 17I) against inhibitor concentration during preincubation result in good estimates of the kinetic parameters without further correction, even when k ctrl is faster than the covalent dissociation rate k 6 (k ctrl > k 6). We strongly advise that enzyme activity be normalized prior to analysis of reversible covalent inhibition even when k ctrl is not directly obvious from the product formation in the uninhibited control vt′ctrl.
Basic Protocol 14: Two-Step Reversible Covalent Inhibition
Processing of experimental data obtained with Basic Protocol III that has been processed according to Basic Data Analysis Protocol 3 for two-step reversible covalent inhibitors.
1.Plot vt′ against preincubation time t′ for each inhibitor concentration.
Plot the mean and standard deviation of vt′ (in AU/s) on the Y-axis against preincubation time t′ (in s) on the X-axis for each inhibitor concentration and the uninhibited control (Fig. 14C/Fig. 17C). Validate that inhibitor concentrations are not too high: inhibition should be less than 100% at the shortest t′ for at least six inhibitor concentrations. Enzyme activity is never truly independent of preincubation time (v0ctrl > vt′ctrl, Fig. 17G) and kinetic analysis of reversible inhibitors is very sensitive to small deviations (illustrated in Fig. 9). Therefore, correction for enzyme instability is always performed by normalization of the enzyme activity vt′/vt′ctrl in the next step (Fig. 17F-J).
2.Normalize vt′ to obtain vt′/vctrl.
Normalize vt′ (in AU/s) of each inhibitor concentration and the controls to lowest value = 0 (or full inhibition control) and highest value = uninhibited product formation vt′ctrl (in AU/s) to obtain normalized enzyme activity vt′/vctrl (Fig. 17H). Perform this correction separately for each preincubation time.
3.Plot and fit vt′/vctrl against preincubation time t′ to obtain k obs and vs/vsctrl.
Plot the mean and standard deviation of vt′/vctrl on the Y-axis against preincubation time t′ (in s) on the X-axis (Fig. 17H). Fit to exponential decay Equation XX to obtain k obs (in s−1) from initial velocity vi/v0ctrl reflecting rapid noncovalent equilibrium (Y-intercept vi/v0ctrl ≤ 1) to the final velocity vs/vsctrl reflecting steady-state equilibrium (Plateau vs/vsctrl ≥ 0).
\begin{equation} \left( {\frac{{{{\rm{v}}{{\rm{t^\prime}}}}}}{{{\rm{v}}{{\rm{t^\prime}}}^{{\rm{ctrl}}}}}} \right) = \left( {\frac{{{{\rm{v}}{\rm{s}}}}}{{{\rm{v}}{\rm{s}}^{{\rm{ctrl}}}}}} \right) + \left( {\frac{{{{\rm{v}}{\rm{i}}}}}{{{\rm{v}}0^{{\rm{ctrl}}}}} - \frac{{{{\rm{v}}{\rm{s}}}}}{{{\rm{v}}{\rm{s}}^{{\rm{ctrl}}}}}} \right){e^{ - {k_{{\rm{obs}}}}{\rm{t^\prime}} }} \end{equation}
Equation XX for nonlinear regression of exponential one-phase decay equation Y = (Y0-Plateau)EXP(-kX) + Plateau with Y = normalized preincubation time–dependent product formation velocity vt′/vctrl (unitless), X = preincubation time t′ (in s) to find Y0 = Y-intercept = normalized initial velocity vi/v0ctrl (unitless), Plateau = normalized final velocity vs/vsctrl = 0 (unitless), and k = observed reaction rate k obs (in s−1).
4.Plot and fit vs/vsctrl against [I] to obtain Ki*.
Steady-state inhibition constant Ki* (in M) can be calculated from vs/vsctrl (obtained in the previous step) reflecting remaining fractional enzyme activity after reaching the steady-state inhibitor equilibrium (reaction completion) (Fig. 17J). Plot the mean and standard deviation of vs/vsctrl on the Y-axis against inhibitor concentration (in M) during preincubation (before addition of substrate) on the X-axis (Fig. 17J), and fit the dose-response curve to four-parameter nonlinear regression Hill Equation XXI (Copeland, 2013e) to obtain steady-state inhibition constant Ki* (in M). The maximum product formation velocity at reaction completion corresponds with the uninhibited enzyme activity vsctrl/vsctrl = 1 and minimum velocity vsmin/vsctrl = 0 for (background-)corrected enzyme activity in the full inhibition control. Steady-state equilibrium constant Ki* (in M) does not does not have to be corrected for substrate competition because preincubation is conducted in absence of competing substrate.
\begin{equation} \left( {\frac{{{{\rm{v}}{\rm{s}}}}}{{{\rm{v}}{\rm{s}}^{{\rm{ctrl}}}}}} \right) = \frac{1}{{1 + {{\left( {\frac{{\left[ {\rm{I}} \right]}}{{{\rm{K}}_{\rm{i}}^{\rm{\star}}}}} \right)}^h}}} \end{equation}
Equation XXI for nonlinear regression of four-parameter dose-response equation Y = Bottom + (Top-Bottom)/(1 + (X/IC50)^HillSlope) with Y = fractional steady-state product formation velocity vs/vsctrl (unitless), X = inhibitor concentration during preincubation (in M), Bottom = velocity in fully inhibited control vsmin/vsctrl = 0 (unitless), and Top = uninhibited enzyme activity vsctrl/vsctrl = 1 (unitless) to find Hillslope = Hill coefficient h (unitless) and IC50 = steady-state inhibition constant Ki* (in M).
5.Optional : Plot and fit k obs against [I] to obtain Ki, k 5, and k 6.
This is an optional data processing step to obtain kinetic parameters by fitting to the observed rate k obs (obtained in Data Analysis 3C , step 3), and can be used to validate Ki* values found in the previous step or to find values for k 5 and k 6 to use in kinetic simulations (next step in this protocol). Plot the mean and standard deviation of k obs (in s−1) on the Y-axis against inhibitor concentration during preincubation (in M) on the X-axis (Fig. 17I). Exclude the uninhibited control (k ctrl = 0 for normalized enzyme activity) from the fit because Y-intercept = k 6 rather than k ctrl. Fit k obs against inhibitor concentration to Equation XXII to obtain rate constants for the covalent association k 5 (in s−1) and covalent dissociation k 6 (in s−1) as well as noncovalent inhibition constant Ki (in M) reflecting the rapid (initial) noncovalent equilibrium. Noncovalent equilibrium constant Ki does not does not have to be corrected for substrate competition because preincubation is conducted in absence of competing substrate. Proceed to Sample Calculation 8 to calculate steady-state inhibition constant Ki* (in M) from experimental values of Ki, k 5, and k 6.
\begin{equation} {k_{{\rm{obs}}}} = {k_6} + \frac{{{k_5}{\rm{;}}\left[ {\rm{I}} \right]}}{{{{\rm{K}}_{\rm{i}}} + \left[ {\rm{I}} \right]}} \end{equation}
Equation XXII for nonlinear regression of user-defined explicit equation Y = Y0 + ((kmax*X)/((Ki) + X)) with Y = observed reaction rate k obs (in s−1) and X = inhibitor concentration during preincubation (in M) to find Y0 = covalent dissociation rate constant k 6 (in s−1), kmax = covalent association rate constant k 5 (in s−1) and Ki = inhibition constant Ki (in M).
6.Optional : Validate experimental kinetic parameters with kinetic simulations.
Proceed to Kinetic Simulations 1 to compare the experimental read-out to the product formation simulated with scripts KinGen and KinDeg to confirm that the calculated kinetic constants are in accordance with the experimental data. Also perform simulations with KinVol and KinVolDeg to confirm that addition of substrate does not significantly affect the noncovalent interactions/equilibria or reaction rates by dilution and/or competition. Experimental estimates of k 5 and k 6 are generated in the previous step of this protocol.
METHOD IV: PREINCUBATION TIME–DEPENDENT INHIBITION WITH DILUTION/COMPETITION
Preincubation time–dependent inhibition with dilution and/or competition is a variant of Method III reported for kinetic analysis of irreversible covalent inhibitors (Kitz & Wilson, 1962). Enzyme and inhibitor are preincubated in absence of competing substrate to form noncovalent EI complex and covalent EI* adduct, followed by dilution in a 10-100-fold larger volume (Vsub >> Vt′) and/or addition of a high concentration of competing substrate ([S] >> KM) (Fig. 18A). The inhibitor concentration after substrate addition is far below the equilibrium concentration ([I]t << 0.1Kiapp), thereby inducing dissociation of inhibitor from the noncovalent inhibitor-enzyme complex EI and quenching the formation of covalent EI* during incubation (Δ[EI*]t = 0). The approach is two-pronged: either dilution (reducing [I]t) or saturating substrate concentration (increasing KIapp and decreasing k chemapp) can be sufficient as long as covalent EI* adduct formation is fully quenched, for example by dissociation of noncovalent EI complex. Preincubation time–dependent product formation velocity vt′ reflects the inhibition by covalent EI* adduct formed during preincubation, and is calculated from the linear slope of product formation (Fig. 18B). Enzyme activity vt′ decreases exponentially from 0% covalent adduct without preincubation (Y-intercept = vctrl) to reach a plateau at 100% covalent adduct upon reaction completion (t′ > 5t½) for irreversible covalent inhibitors (Fig. 18C). Observed rate of reaction completion k obs (from 0-100% inhibition) is obtained by fitting to bounded exponential decay Equation VI (Fig. 18D). This is a simplified version of Equation V (Fig. 14D) in Method III (constraining vs = 0) because we only consider two-step irreversible inhibition (Data Analysis 4A) and one-step irreversible inhibition (Data Analysis 4B). Reversible (two-step) covalent inhibition with a slow rate of covalent dissociation k 6 (t½diss = LN(2)/k 6) can be analyzed with preincubation dilution assays using the initial product formation velocity after rapid/jump dilution (Copeland, 2013e; Copeland et al., 2011) but will not be discussed here because the (slow) dissociation of covalent EI* adduct can complicate the algebraic analysis.
![Details are in the caption following the image Method IV: Preincubation time–dependent inhibition with dilution/competition. Simulated with KinVol for 100 pM enzyme and 50 nM two-step irreversible inhibitor C (before dilution) in V<sub>t′</sub> = 1 and 10 µM substrate S1 in V<sub>sub</sub> = 99 corresponding with 100-fold dilution in excess substrate ([S] = 10K<sub>M</sub>). (A) Enzyme is preincubated with inhibitor to form noncovalent complex EI and covalent adduct EI* in absence of competing substrate, followed by dilution in excess substrate. Initial noncovalent EI complex forms rapidly ([I]<sub>t′</sub>/K<sub>i</sub> = 0.5) but fully dissociates upon dilution in a large volume (V<sub>sub</sub> >> V<sub>t′</sub>) and/or addition of a high concentration of competing substrate ([S] > K<sub>M</sub>), as the E + I <-> EI equilibrium has shifted towards fully unbound enzyme ([I]<sub>t</sub>/K<sub>i</sub><sup>app</sup> << 0.1). (B) Preincubation time–dependent enzyme activity v<sub>t′</sub> (in AU/s) is obtained from the (linear) slope of product formation velocity. Dilution in excess substrate quenches EI* formation after substrate addition (ΔEI* = 0), thus enabling longer incubation times compared to Method III. This measurement must be performed separately after each preincubation time. (C) Enzyme activity v<sub>t′</sub> decreases exponentially from 0% covalent adduct (Y-intercept = enzyme activity without preincubation v<sub>i</sub>) to 100% covalent adduct (v<sub>s</sub> = 0). Enzyme activity without preincubation v<sub>i</sub> equals the uninhibited enzyme activity v<sup>ctrl</sup> for one-step as well as two-step irreversible inhibitors: dilution in excess substrate should induce full dissociation of noncovalently bound inhibitor ([I]<sub>t</sub> << 0.1K<sub>i</sub><sup>app</sup>), and covalent adduct does not form instantly. (D) Bounded exponential decay Equation VI to fit preincubation time–dependent enzyme activity v<sub>t′</sub> (in AU/s) after dilution in (excess) competing substrate against preincubation time t′ (in s) for irreversible one- and two-step inhibition. This is a simplified version of Equation V (Fig. 14D) constraining v<sub>s</sub> = 0 (inactivation at reaction completion). v<sub>i</sub> = enzyme activity without preincubation (in AU/s) = uninhibited enzyme activity v<sup>ctrl</sup> because covalent adduct has not yet been formed and noncovalent complex has been disrupted by dilution in excess substrate. v<sub>t′</sub> = preincubation time–dependent enzyme activity (in AU/s) reflecting covalent EI* adduct formed. t′ = preincubation time of enzyme and inhibitor before substrate addition (in s). k<sub>obs</sub> = observed rate of time-dependent inhibition from initial v<sub>i</sub> to final v<sub>s</sub> (in s<sup>−1</sup>).](https://static.yanyin.tech/literature_test/cpz1419-fig-0018-m.jpg)
Generally, preincubation assays are disfavored because their experimental execution requires more material and measurements than incubation assays with continuous read-out. However, as already mentioned in Method III , preincubation methods are favored for inhibitors that have a slow covalent reaction rate and/or a poor noncovalent affinity. Additionally, dilution in excess substrate can resolve issues for enzyme assays that do not generate enough product for a robust signal (slow vctrl), as the maximum incubation time to calculate vt′ is not limited by formation of EI* during incubation (Δ[EI*]t = 0): incubation time can be longer than preincubation time. It is important to mention that there is still a limit to the incubation time: competition and/or dilution cannot fully mitigate the covalent adduct formation reaction but it can be reduced to a negligible rate during the incubation. Finally, this method allows the assessment of covalent adduct formation potency without contamination by reversible inhibition. This can be beneficial in the analysis of two-step covalent inhibitors that exhibit tight-binding behavior (customary for kinase inhibitors that have to compete with ATP): very potent noncovalent affinity ‘shields’ or ’contaminates’ the rate of covalent adduct formation in the other protocols but not in this method, as detection is based solely on inhibition by covalent EI* adduct. However, the enzyme concentration during incubation is much lower than during preincubation, and inhibitor has to be present in excess during preincubation (pseudo-first order conditions), thus limiting the inhibitor concentration to higher concentrations than with other methods, which might be impractical.
Be aware that dilution in (excess) substrate will change the absolute enzyme/inhibitor concentrations from preincubation to incubation, and make sure to calculate the desired enzyme concentration during incubation accordingly. Reaction completion (vt′ < 0.1vctrl) should not be reached before the first (shortest) preincubation time because it will be impossible to detect time-dependent changes in enzyme activity. This can be resolved by increasing the measurement interval (shorter dt′) or reducing the inhibitor concentration whenever possible. This method is less suitable for inhibitors with a very fast covalent adduct formation k inact because preincubation is performed in absence of competing substrate (thus allowing the maximum rate of covalent adduct formation possible at this inhibitor concentration).
Basic Protocol 15: Preincubation Time–Dependent Inhibition with Dilution/Competition
The protocol below provides a generic set of steps to accomplish this type of measurement. Specific reagents, and assay conditions for preincubation time–dependent inhibition with dilution of two-step irreversible covalent acetylcholinesterase inhibitors, can be found in Kitz & Wilson (1962).
Materials
- 1× Assay/reaction buffer supplemented with co-factors and reducing agent
- Active enzyme, 200× solution in assay buffer
- Substrate with continuous or quenched read-out, 1× solution in assay buffer
- Positive control: vehicle/solvent as DMSO stock, or 2% solution in assay buffer
- Negative control: known inhibitor or alkylating agent as DMSO stock, or 200× solution in assay buffer
- Inhibitor: as DMSO stock, or serial dilution of 200× solution in assay buffer with 2% DMSO
- Optional : Development/quenching solution
- 1.5 ml (Eppendorf) microtubes to prepare stock solutions
- 384-well low volume microplate with nonbinding surface (e.g., Corning 3820 or 4513) for preincubation
- General microplate cover/lid (e.g., Corning 6569 Microplate Aluminum Sealing Tape) to seal 384-well plate during preincubation
- 96-well low volume microplate with nonbinding surface (e.g., Corning 3650 or 3820) for quenching and read-out
- Optional : 96-well microplate to prepare serial dilution of inhibitor concentration
- Optional : Microtubes to perform preincubations (e.g., Eppendorf Protein Lobind Microtubes, #022431018)
- Optional : 384-well low volume microplate with nonbinding surface (e.g., Corning 3820 or 4513) for read-out
- Microplate reader equipped with appropriate filters to detect product formation (e.g., CLARIOstar microplate reader)
- Optional : Automated (acoustic) dispenser (e.g., Labcyte ECHO 550 Liquid Handler acoustic dispenser)
Before you start , optimize assay conditions in the uninhibited control to ensure compliance with assumptions and restrictions, as outlined in Basic Protocol I. Consult Table 3 in the troubleshooting section for common optimization and troubleshooting options.
Specific adjustments for Method IV
Substrate should be added in a large volume (Vsub >> Vt′) and/or at a high concentration ([S]0 >> KM) to quench time-dependent enzyme inhibition (Fig. 18A). Enzyme concentration after dilution [Etotal]t should be adjusted to correspond to maximum 10% substrate conversion until the end of the incubation in the uninhibited control ([P]t < 0.1[S]0), and substrate should be present in excess ([S]0 > 10[Etotal]t). Preincubation-dependent enzyme activity should be calculated from initial, linear product formation after substrate addition. Validate that enough product is formed for a good signal/noise ratio (Z′ > 0.5) by calculating the Z′-score from the uninhibited and inhibited controls (ideally 8 replicates) in a separate experiment (Zhang et al., 1999). This method is compatible with homogeneous (continuous) assays but also with assays that require a development/quenching step to visualize formed product. Note that preincubation in very small volumes (<10 µl) is not representative/reliable and the volume after 100-fold dilution in substrate will often exceed the maximum well volume of assay plates. Therefore, preincubation is typically performed in a larger volume (tube or plate) from which aliquots are removed at the end of the preincubation. In this protocol, we perform incubations in triplicate (20 µl per replicate) in a 384-well plate, from which 2-µl aliquots are removed and quenched in 198 µl substrate in a 96-well plate that is also used for read-out. Optionally, it is possible to then transfer 20 µl to a 384-well plate for read-out, but multiple transfers of assays solutions will introduce errors. Alternatively, preincubation can be performed in microtubes or a 96-well plate.
1.Add inhibitor or control (e.g., 0.2 µl) and assay buffer (e.g., 10 µl) to each well with the uninhibited control for full enzyme activity containing the same volume vehicle/solvent instead of inhibitor, as outlined in step 1 of Basic Protocol III.
Gently shake to mix DMSO with the aqueous buffer. Typically, measurements are performed in triplicate (or more replicates) with at least 8 inhibitor concentrations for at least 5 preincubation times. Inhibitor concentrations might need optimization, but a rational starting point is to use inhibitor concentrations below 5 times the IC50 at the shortest preincubation time t′: inhibition is expected to improve in a time-dependent manner, and the best results are obtained when full inhibition is not achieved already at the shortest preincubation time (Fig. 18C). Whether preincubation is performed in a tube or microplate is a matter of personal preference, compatibility with lab equipment and automation, and convenience of dispensing small volumes.
2.Add active enzyme in assay buffer to each well (e.g., 10 µl of 200× solution) or tube to start preincubation of enzyme with inhibitor and homogenize the solution by gently shaking (1 min at 300 rpm). Alternatively, dispensing the enzyme at a high flow rate will also mix the components.
The order of enzyme and inhibitor addition is not important per se , as long as DMSO stocks are added prior to buffered (aqueous) solutions. Inhibitor must be present in excess during preincubation ([I]0 > 10[E]0). Optionally, gently centrifuge the plate or microtubes (1 min at 1000 rpm) to ensure assay components are not stuck at the top of the well.
3.Seal the wells with a cover or lid, and close the caps of microtubes to prevent evaporation of assay components during preincubation.
4.Remove a single aliquot in volume Vt′ (e.g., 2 µl) from the reaction mixture, and transfer to a 96-well microplate already containing a large volume (volume Vsub) of substrate (e.g., 198 µl of 1× solution in assay buffer) after preincubation time t′.
Substrate should be added in a large volume (V t << Vt′) and/or at a high concentration ([S] >> KM) to quench time-dependent addition enzyme inhibition during incubation by dilution ([I]t << [I]t′) or competition (increasing KIapp or decreasing k chemapp). Dilution to inhibitor concentration far below the equilibrium concentration ([I]t << Kiapp) promotes dissociation of noncovalently bound inhibitor after substrate addition (Fig. 18A). The accuracy of the measurement improves if the preincubation time is monitored precisely. Optionally, homogenize the solutions by gentle shaking (300 rpm) and centrifuge the plate (1 min at 1000 rpm) to ensure assay components are not stuck at the top of the well.
5.Quenching : Add development solution to the reaction mixture in the microplate to quench the product formation reaction if read-out of product formation requires a development/quenching step to visualize formed product after incubation time t.
Follow manufacturer's advice on waiting time after addition of development solution before read-out. Incubation time t is the elapsed time between onset of product formation by substrate addition (step 4) and addition of development/quenching solution (step 5). A possible advantage to the use of a quenched assay is the ability to store the samples after addition of quenching/development solution (step 5) and measure product formation (step 6) in all samples after completion of the final preincubation rather than performing multiple separate measurements (after each preincubation time).
6.Optional : Transfer aliquot (e.g., 20 µl) to a 384-well microplate for read-out.
Typically, the total volume after dilution in substrate solution (V t = Vsub + Vt′) exceeds the maximum well volume of a 384-well microplate. Transfer an appropriate amount of reaction mixture (at least two technical replicates) to a microplate. This step can be skipped if read-out is performed in a 96-well plate.
7.Measure formed product after incubation by detection of the product read-out in microplate reader.
Incubation time t (after substrate addition) is arbitrary as long as product formation is linear in uninhibited as well as inhibited samples (Fig. 18B).
8.Repeat Basic Protocol IV , steps 4-7, for at least another four preincubation times.
Preincubation time t′ is the elapsed time between onset of inhibition by mixing enzyme and inhibitor (step 2) and addition of substrate (step 4). A typical preincubation assay is multiple hours measuring enzyme activity every 5-30 min, depending on enzyme stability and inhibitor reaction rates. Best results are obtained if the incubation time t used to calculate enzyme activity is kept constant at all preincubation times.
9.Proceed to Basic Data Analysis Protocol 4 to convert the raw experimental data into preincubation time–dependent enzyme activity.
Basic Protocol 16: Preincubation Time–Dependent Inhibition With Dilution
Processing of raw experimental data obtained with Basic Protocol IV for irreversible inhibitors.
1.Plot signal F against incubation time t.
Plot signal F (in AU) on the Y-axis against the incubation time (in s) on the X-axis for each inhibitor concentration and for the controls (Fig. 19B, Fig. 20B). Do this separately for each preincubation time.
![Details are in the caption following the image Data Analysis 4A: Preincubation time–dependent inhibition with dilution/competition for two-step irreversible covalent inhibition. Simulated with KinVol (A-D) or KinVolDeg (E-I) for inhibitor C with 100 pM enzyme in V<sub>t′</sub> = 1 ([E<sup>total</sup>]<sub>t′</sub> = 100, [E<sup>total</sup>]<sub>t</sub> = 1) and 10 µM substrate S1 ([S] = 10K<sub>M</sub>) in V<sub>sub</sub> = 99. (A) Schematic enzyme dynamics during preincubation in absence of substrate and during incubation after dilution in excess substrate for two-step irreversible covalent inhibition. (B) Time-dependent product formation after preincubation (t′ = 1800 s) in absence of inhibitor F<sup>ctrl</sup> or in presence of various inhibitor concentrations. Enzyme activity after preincubation v<sub>t′</sub> is obtained from the linear slope. (C) Preincubation time–dependent enzyme activity v<sub>t′</sub> is fitted to Equation VI (Fig. 18D) for each inhibitor concentration with global shared value for v<sub>i</sub> (v<sub>i</sub> = v<sup>ctrl</sup>) to obtain observed rates of inactivation k<sub>obs</sub>. Alternatively, v<sub>t′</sub> can be normalized to a fraction of the uninhibited enzyme activity v<sup>ctrl</sup>. (D) Half-maximum k<sub>obs</sub> = ½k<sub>inact</sub> is reached when inhibitor concentration during preincubation equals the inactivation constant K<sub>I</sub>: no correction for substrate competition because v<sub>t′</sub> reflects the remaining unbound/noncovalent enzyme activity after preincubation in absence of competing substrate. (E) Schematic enzyme dynamics during preincubation in absence of substrate and during incubation after dilution in excess substrate for two-step irreversible covalent inhibition with spontaneous enzyme degradation/denaturation. Simulated with k<sub>degE</sub> = k<sub>degES</sub> = k<sub>degEI</sub> = 0.0003 s<sup>−1</sup>. (F) Uninhibited enzyme activity after preincubation v<sub>t′</sub><sup>ctrl</sup> decreases with longer preincubation. Enzyme activity v<sub>t′</sub> is fitted to Equation VI (Fig. 18D) for each inhibitor concentration during preincubation with globally shared value for v<sub>i</sub> (v<sub>i</sub> = v<sub>0</sub><sup>ctrl</sup>) to obtain observed rates of inactivation k<sub>obs</sub>, as well as fitting uninhibited activity v<sub>t′</sub><sup>ctrl</sup> to obtain the rate of nonlinearity k<sub>ctrl</sub>. (G) Inhibitor concentration-dependent k<sub>obs</sub> with spontaneous enzyme degradation increases with k<sub>ctrl</sub> but the span from k<sub>min</sub> (= k<sub>ctrl</sub>) to k<sub>max</sub> (= k<sub>inact</sub> + k<sub>ctrl</sub>) still equals k<sub>inact</sub>. Fit with algebraic correction for nonlinearity (black line, k<sub>ctrl</sub> > 0). Ignoring the nonlinearity (gray line, constrain k<sub>ctrl</sub> = 0) results in underestimation of K<sub>I</sub> (overestimation of potency) and overestimation of k<sub>inact</sub>. (H) Normalized enzyme activity v<sub>t′</sub>/v<sup>ctrl</sup> is fitted to Equation VI (Fig. 18D) for each inhibitor concentration during preincubation (constrain v<sub>i</sub>/v<sub>0</sub><sup>ctrl</sup> = 1) to obtain corrected observed rates of inactivation k<sub>obs</sub>. (I) Inhibitor concentration-dependent k<sub>obs</sub> has been corrected for enzyme degradation by fitting normalized enzyme activity v<sub>t′</sub>/v<sup>ctrl</sup> and does not require further corrections.](https://static.yanyin.tech/literature_test/cpz1419-fig-0019-m.jpg)
![Details are in the caption following the image Data Analysis 4B: Preincubation time–dependent inhibition with dilution/competition for one-step irreversible covalent inhibition. Simulated with KinVol (A-D) or KinVolDeg (E-I) for inhibitor D with 100 pM enzyme in V<sub>t′</sub> = 1 ([E<sup>total</sup>]<sub>t′</sub> = 100, [E<sup>total</sup>]<sub>t</sub> = 1) and 10 µM substrate S1 ([S] = 10K<sub>M</sub>) in V<sub>sub</sub> = 99. (A) Schematic enzyme dynamics during preincubation in absence of substrate and during incubation after dilution in excess substrate for one-step irreversible covalent inhibition. (B) Time-dependent product formation after preincubation (t′ = 1800 s) in absence of inhibitor F<sup>ctrl</sup> or in presence of various inhibitor concentrations. Enzyme activity after preincubation v<sub>t′</sub> is obtained from the linear slope. (C) Preincubation time–dependent enzyme activity v<sub>t′</sub> is fitted to Equation VI (Fig. 18D) for each inhibitor concentration with global shared value for v<sub>i</sub> (v<sub>i</sub> = v<sup>ctrl</sup>) to obtain observed rates of inactivation k<sub>obs</sub>. Alternatively, v<sub>t′</sub> can be normalized to a fraction of the uninhibited enzyme activity v<sup>ctrl</sup>. The highest inhibitor concentration should be excluded: v<sub>600</sub> = 0. (D) Inhibitor concentration-dependent k<sub>obs</sub> increases linearly with inhibitor concentration during preincubation, with k<sub>chem</sub> as the slope. No correction for substrate competition because v<sub>t′</sub> reflects the remaining unbound enzyme activity after preincubation in the absence of competing substrate. (E) Schematic enzyme dynamics during preincubation in absence of substrate and during incubation after dilution in excess substrate for one-step irreversible covalent inhibition with spontaneous enzyme degradation/denaturation. Simulated with k<sub>degE</sub> = k<sub>degES</sub> = k<sub>degEI</sub> = 0.0003 s<sup>−1</sup>. (F) Uninhibited enzyme activity after preincubation v<sub>t′</sub><sup>ctrl</sup> decreases with longer preincubation. Enzyme activity v<sub>t′</sub> is fitted to Equation VI (Fig. 18D) for each inhibitor concentration during preincubation with globally shared value for v<sub>i</sub> (v<sub>i</sub> = v<sub>0</sub><sup>ctrl</sup>) to obtain observed rates of inactivation k<sub>obs</sub>, along with fitting uninhibited activity v<sub>t′</sub><sup>ctrl</sup> to obtain the rate of nonlinearity k<sub>ctrl</sub>. (G) Inhibitor concentration-dependent k<sub>obs</sub> with spontaneous enzyme degradation/denaturation increases by k<sub>ctrl</sub>. Fit with algebraic correction for nonlinearity (black line, k<sub>ctrl</sub> > 0) or ignoring nonlinearity (gray line, constrain k<sub>ctrl</sub> = 0). Ignoring the nonlinearity (assuming Y-intercept = 0) results in overestimation of k<sub>chem</sub> (steeper slope). (H) Normalized enzyme activity v<sub>t′</sub>/v<sup>ctrl</sup> is fitted to Equation VI (Fig. 18D) for each inhibitor concentration during preincubation (constrain v<sub>i</sub>/v<sub>0</sub><sup>ctrl</sup> = 1) to obtain corrected observed rates of inactivation k<sub>obs</sub>. (I) Inhibitor concentration-dependent k<sub>obs</sub> has been corrected for enzyme degradation by fitting normalized enzyme activity v<sub>t′</sub>/v<sup>ctrl</sup> and does not require further corrections.](https://static.yanyin.tech/literature_test/cpz1419-fig-0020-m.jpg)
2.Fit F t against t to obtain vt′.
Fit signal F t against incubation time t to Equation XIII (Fig. 19B, Fig. 20B) to obtain preincubation time–dependent product formation velocity vt′ (in AU/s) from the linear slope (Fig. 18B). Linear product formation is indicative of effective disruption of additional covalent modification during incubation by dilution in excess substrate (Fig. 18A). If product formation is not linear: consult Table 3 for troubleshooting or proceed to Basic Data Analysis Protocol 3.
\begin{equation*} {F_t} = {F_0} + {{\rm{v}}_{{\rm{t^\prime}}}}t \end{equation*}
Equation XIII for nonlinear regression of straight line Y = YIntercept + Slope*X with Y = signal F t (in AU) and X = incubation time t (in s) to find YIntercept = background signal at reaction initiation F 0 (in AU) and Slope = preincubation time–dependent product formation velocity vt′ (in AU/s).
3.Proceed to Data Analysis Protocols to obtain the appropriate kinetic parameters for each covalent binding mode: Data Analysis Protocol 4Ai or 4Aii for two-step irreversible inhibitors and Data Analysis Protocol 4Bi or 4Bii for one-step irreversible inhibitors.
Selection of a Data Analysis Method for inhibitors with an irreversible binding mode depends on the desired visual representation as well as personal preference. Generally, Basic Data Analysis Protocols 4Ai and 4Bi have less data processing/manipulation and are more informative for comparison of various inhibitors on a single enzyme target, as they are compatible with assessment of inhibitor potency simultaneous with visual assessment of time-dependent enzyme stability k ctrl (Fig. 19F and 19G and Figs. 20F and 20G). Alternative Data Analysis Protocols 4Aii and 4Bii involve normalization of the enzyme activity that aids visual assessment of inhibitory potency of a single inhibitor on multiple enzyme targets (that might have a variable stability) (Fig. 19H and 19I and Fig. 20H and 20I).
| Data Analysis Protocol | |||
|---|---|---|---|
| EXP Conditions | 2-step IRREV | 1-step IRREV | 2-step REV |
| kctrl = 0 | 4Ai/4Aii | 4Bi/4Bii | – |
| kdegE > 0 | 4Ai/4Aii | 4Bi/4Bii | – |
Exemplary assay concentrations during preincubation and during incubation.
| Concentration during preincubation t′ | Concentrations during incubation t | |||||
|---|---|---|---|---|---|---|
| [stock] | V (µl) | [conc]t′ | [stock] | V (µl) | [conc]t | |
| Enzyme | 200 nM | 10 | 99 nM | – | 1 | 1.0 nM |
| Inhibitor | 2000 nM | 10.2 | 1010 nM | – | 1 | 10 nM |
| Substrate | – | – | – | 10 µM | 198 | 9.9 µM |
| Total | 20.2 | 200 | ||||
Data Analysis 4A: Preincubation Time–Dependent Inhibition With Dilution/Competition for Two-Step Irreversible Covalent Inhibition
Kinetic analysis of enzyme activity with dilution/competition after preincubation in the presence of a two-step covalent inhibitor is similar to data analysis of preincubation without dilution/competition (Data Analysis 3A), with the exception that longer incubation times are possible to calculate enzyme activity vt′ from the slope (Fig. 19A and 19B), and enzyme activity without preincubation vi should be equal to the uninhibited enzyme activity vctrl (Fig. 19C). Contrary to Method III , this does not imply that the inhibitors show one-step behavior: it merely confirms that extensive dilution/substrate competition successfully induced inhibitor dissociation from noncovalent EI complex to unbound enzyme. It is essential to plot the rate of covalent adduct formation k obs against the inhibitor concentration during preincubation (Fig. 19D) to obtain kinetic parameters: k obs is based on the formation of EI* during preincubation, and the inhibitor concentration during preincubation is much higher than the inhibitor concentration after dilution in substrate ([I]t′ >> [I]t).
Warnings and remarks
Insufficient dilution/competition will partially disrupt noncovalent EI complex, resulting in a time-dependent decrease of enzyme activity due to formation of EI* after substrate addition (Fig. 19B) and deviation from vi = vctrl, as noncovalent complex EI contributes to inhibition without preincubation (Fig. 19C). Increasing substrate concentration and/or dilution in a larger volume might resolve this. Alternatively, enzyme activity with partial disruption of noncovalent EI analyzed with Data Analysis 3A still results in reliable estimates of k obs. Please note that, although detection based only on covalent adduct formation allows analysis of two-step inhibitors displaying tight-binding behavior (very high noncovalent affinity resulting in full inhibition at all inhibitor concentrations), these inhibitor concentrations are saturating if they comply with the rapid equilibrium approximation (Ki ≈ KI); thus, it would only be possible to determine the lower limit of k inact and the upper limit of KI (Fig. 2G).
Correction for enzyme (in)stability during preincubation by correcting for the rate of spontaneous degradation k ctrl has been reported (Obach, Walsky, & Venkatakrishnan, 2007) for dilution experiments with irreversible covalent inhibitors (Fig. 19E-G). Alternatively, enzyme activity after preincubation vt′ can be normalized to the uninhibited enzyme activity after preincubation vt′ctrl (Fig. 19H and 19I).
Basic Protocol 17: Two-Step Irreversible Covalent Inhibition
Processing of experimental data obtained with Basic Protocol IV that has been processed according to Basic Data Analysis Protocol 4 for two-step irreversible inhibitors.
1.Plot vt′ against preincubation time t′ for each inhibitor concentration.
Plot the mean and standard deviation of vt′ (in AU/s) on the Y-axis against preincubation time t′ (in s) on the X-axis for each inhibitor concentration and the uninhibited control (Fig. 19C). Validate that inhibitor concentrations are not too high: inhibition should be less than 100% at the shortest t′ for at least six inhibitor concentrations. Check whether the uninhibited enzyme activity is independent of preincubation time (v0ctrl = vt′ctrl, Fig. 19C): an algebraic correction for enzyme instability (k ctrl > 0, Fig. 19F) can be performed in step 4 of this protocol by accounting for nonlinearity in the uninhibited control in the secondary k obs plot (Fig. 19G). Alternatively, proceed to Alternative Data Analysis Protocol 4Bii to correct for enzyme instability (v0ctrl > vt′ctrl) by normalization of the enzyme activity vt′/vt′ctrl (Fig. 19H and 19I).
2.Fit vt′ against preincubation time t′ to obtain k obs.
Fit the mean and standard deviation of vt′ against preincubation time t′ (Fig. 19C/F) for each inhibitor concentration to bounded exponential decay Equation VI (Fig. 18D) with shared value for initial velocity vi to obtain the observed reaction rate k obs (in s−1) from initial velocity vi (Y-intercept) to full inactivation (vs in fully inhibited control). A lack of initial noncovalent complex (vi = v0ctrl) is indicative of effective disruption of noncovalent interactions by dilution in excess substrate. Validate this by fitting without constraints for vi. Proceed to Basic Data Analysis Protocol 3Ai if deviations (vi < v0ctrl) are observed.
\begin{equation} {{\rm{v}}_{{\rm{t^\prime}}}} = {\rm{v}}0^{{\rm{ctrl}}};{e^{ - {k{{\rm{obs}}}}{\rm{t^\prime}}}} \end{equation}
Equation VI for nonlinear regression of exponential one-phase decay equation Y = (Y0-Plateau)EXP(-kX) + Plateau with Y = preincubation time–dependent product formation velocity vt′ (in AU/s), X = preincubation time t′ (in s) and Plateau = final velocity vs = 0 or vs in fully inhibited control (in AU/s) to find Y0 = Y-intercept = initial velocity vi = uninhibited velocity v0ctrl (in AU/s, shared value) and k = observed reaction rate k obs (in s−1).
3.Plot k obs against [I].
Plot the mean and standard deviation of k obs (in s−1) on the Y-axis against inhibitor concentration (in M) during preincubation (before addition of substrate) on the X-axis (Fig. 19D/G). The plot of k obs against [I] should reach a maximum k obs at saturating inhibitor concentration. Note that a linear curve is indicative of one-step binding behavior at non-saturating inhibitor concentrations ([I] << 0.1KI in Fig. 3F) with vi = v0ctrl (shared Y-intercept in the previous step). Proceed to Basic Data Analysis Protocol 4Bi step 4 after it has been validated that the linear curve is not resultant from saturating inhibitor concentrations ([I] >> 10KI in Fig. 3G) as identified by vi << v0ctrl, by repeating the measurement with lower inhibitor concentrations.
4.Fit k obs against [I] to obtain k inact and KI.
Fit k obs against inhibitor concentration during preincubation to Equation XV to obtain maximum inactivation rate constant k inact (in s−1) and inactivation constant KI (in M). Constrain k ctrl = k obs of the uninhibited control (Fig. 19G). Inactivation constant KI does not have to be corrected for substrate competition because preincubation is conducted in absence of competing substrate. Calculate irreversible covalent inhibitor potency k inact/KI (in M−1s−1) with propagation of error with Sample Calculation 2.
\begin{equation} {k_{{\rm{obs}}}} = {k_{{\rm{ctrl}}}} + \frac{{{k_{{\rm{inact}}}}{\rm{;}}\left[ {\rm{I}} \right]}}{{{{\rm{K}}_{\rm{I}}} + \left[ {\rm{I}} \right]}};; \end{equation}
Equation XV for nonlinear regression of user-defined explicit equation Y = Y0 + ((kmax*X)/((KI) + X)) with Y = observed reaction rate k obs (in s−1) and X = inhibitor concentration during preincubation (in M) to find Y0 = rate of nonlinearity in uninhibited control k ctrl (in s−1), kmax = maximum reaction rate k inact (in s−1), and KI = Inactivation constant KI (in M).
5.Optional : Validate experimental kinetic parameters with kinetic simulations.
Proceed to Kinetic Simulations 1 to compare the experimental read-out to the product formation simulated with scripts KinVol and KinVolDeg (using experimental rate constant k inact = k 5) to confirm that the calculated kinetic constants are in accordance with the experimental data.
Basic Protocol 18: Two-Step Irreversible Covalent Inhibition
Processing of experimental data obtained with Basic Protocol IV that has been processed according to Basic Data Analysis Protocol 4 for two-step irreversible inhibitors.
1.Plot vt′ against preincubation time t′ for each inhibitor concentration.
Plot the mean and standard deviation of vt′ (in AU/s) on the Y-axis against preincubation time t′ (in s) on the X-axis for each inhibitor concentration and the uninhibited control (Fig. 19C). Validate that inhibitor concentrations are not too high: inhibition should be less than 100% at the shortest t′ for at least six inhibitor concentrations.
2.Normalize vt′ to obtain vt′/vctrl.
Normalize vt′ (in AU/s) of each inhibitor concentration and the controls to lowest value = 0 (or full inhibition control) and highest value = uninhibited product formation vt′ctrl (in AU/s) to obtain normalized enzyme activity vt′/vctrl (Fig. 19H). Perform this correction separately for each preincubation time.
3.Plot and fit vt′/vctrl against preincubation time t′ to obtain k obs.
Plot the mean and standard deviation of vt′/vctrl on the Y-axis against preincubation time t′ (in s) on the X-axis (Fig. 19H). Fit to exponential decay Equation XVI to obtain k obs (in s−1) from initial velocity vi/v0ctrl to full inactivation (Plateau = 0). A lack of initial noncovalent complex (vi = v0ctrl) is indicative of effective disruption of noncovalent interactions by dilution in excess substrate. Validate this by fitting without constraints for vi. Proceed to Basic Data Analysis Protocol 3Aii if deviations (vi < v0ctrl) are observed.
\begin{equation} \left( {\frac{{{{\rm{v}}{{\rm{t^\prime}}}}}}{{{\rm{v}}{{\rm{t^\prime}}}^{{\rm{ctrl}}}}}} \right) = {e^{ - {k_{{\rm{obs}}}}{\rm{t^\prime}} }} \end{equation}
Equation XVI for nonlinear regression of exponential one-phase decay equation Y = (Y0-Plateau)EXP(-kX) + Plateau with Y = normalized preincubation time–dependent product formation velocity vt′/vctrl (unitless), X = preincubation time t′ (in s), Y0 = Y-intercept = normalized initial velocity vi/v0ctrl = 1 (unitless), and Plateau = normalized final velocity vs/vsctrl = 0 (unitless) to find k = observed reaction rate k obs (in s−1).
4.Plot k obs against [I].
Plot the mean and standard deviation of k obs (in s−1) on the Y-axis against inhibitor concentration (in M) during preincubation (before addition of substrate) on the X-axis (Fig. 19I). The plot of k obs against [I] should reach a maximum k obs at saturating inhibitor concentration. Note that a linear curve is indicative of one-step binding behavior at non-saturating inhibitor concentrations ([I] << 0.1KI in Fig. 3F) with vi = v0ctrl (shared Y-intercept = 1 in the previous step). Proceed to Basic Data Analysis Protocol 4Bii step 5 after it has been validated that the linear curve is not resultant from saturating inhibitor concentrations ([I] >> 10KI in Fig. 3G) as identified by vi << v0ctrl (shared Y-intercept = 0 in the previous step), by repeating the measurement with lower inhibitor concentrations.
5.Fit k obs against [I] to obtain k inact and KI.
Fit k obs against inhibitor concentration during preincubation to Equation XVII to obtain maximum inactivation rate constant k inact (in s−1) and inactivation constant KI (in M) (Fig. 19I). Do not correct for enzyme instability (k ctrl > 0), as this correction has already been performed by normalizing vt′. Inactivation constant KI does not have to be corrected for substrate competition because preincubation is conducted in absence of competing substrate. Calculate irreversible covalent inhibitor potency k inact/KI (in M−1s−1) with propagation of error with Sample Calculation 2
\begin{equation} {k_{{\rm{obs}}}} = \frac{{{k_{{\rm{inact}}}}{\rm{;}}\left[ {\rm{I}} \right]}}{{{{\rm{K}}_{\rm{I}}} + \left[ {\rm{I}} \right]}};; \end{equation}
Equation XVII for nonlinear regression of user-defined explicit equation Y = Y0+((kmax*X)/((KI) + X)) with Y = observed reaction rate k obs (in s−1), X = inhibitor concentration during preincubation (in M), and Y0 = 0 (in s−1) to find kmax = maximum reaction rate k inact (in s−1) and KI = Inactivation constant KI (in M).
6.Optional : Validate kinetic parameters with kinetic simulations by proceeding to Basic Data Analysis Protocol 4Ai step 5.
Data Analysis 4B: Preincubation Time–Dependent Inhibition With Dilution/Competition for One-Step Irreversible Covalent Inhibition
Kinetic analysis of enzyme activity with dilution/competition after preincubation in presence of a one-step covalent inhibitor is almost identical to data analysis of preincubation without dilution in excess substrate (Data Analysis 3B), with the exception that longer incubation times are possible to calculate enzyme activity vt′ from the slope (Fig. 20A-C). It is essential to plot the rate of covalent adduct formation k obs against the inhibitor concentration during preincubation (Fig. 20D) to obtain kinetic parameters: k obs is based on the formation of EI* during preincubation, and the inhibitor concentration during preincubation will be much higher than the inhibitor concentration after dilution in substrate ([I]t′ >> [I]t).
Warnings and remarks
Dilution/competition does not disrupt any noncovalent EI complex, as this is non-existent for one-step inhibitors, but the rate of covalent adduct formation k obs should be negligible after dilution in excess substrate, to prevent formation of covalent EI*. Insufficient dilution and/or competition (Δ[EI*]t > 0) can result in time-dependent decrease of enzyme activity due to formation of EI* after substrate addition (Fig. 20B). Increasing substrate concentration and/or dilution in a larger volume might resolve this if necessary, but simply performing analysis with Data Analysis Protocol 3B also results in reliable estimates of k obs. Inhibitor concentrations that reach reaction completion during the shortest preincubation time should be excluded from the fit (highest concentration in Fig. 20C) as these fits are not reliable.
Correction for enzyme (in)stability during preincubation by correcting for the rate of spontaneous degradation k ctrl has been reported (Obach et al., 2007) for dilution experiments with irreversible covalent inhibitors (Fig. 20E-G). Alternatively, enzyme activity after preincubation vt′ can be normalized to the uninhibited enzyme activity after preincubation vt′ctrl (Fig. 20H and 20I).
Basic Protocol 19: One-Step Irreversible Covalent Inhibition
Processing of experimental data obtained with Basic Protocol IV that has been processed according to Basic Data Analysis Protocol 4 for one-step irreversible covalent inhibitors and two-step irreversible inhibitors at non-saturating inhibitor concentrations ([I] ≤ 0.1KI).
1.Plot vt′ against preincubation time t′ for each inhibitor concentration.
Plot the mean and standard deviation of vt′ (in AU/s) on the Y-axis against preincubation time t′ (in s) on the X-axis for each inhibitor concentration and the uninhibited control (Fig. 20C). Validate that inhibitor concentrations are not too high: inhibition should be less than 100% at the shortest t′ for at least six inhibitor concentrations. Check whether the uninhibited enzyme activity is independent of preincubation time (v0ctrl = vt′ctrl, Fig. 20C): an algebraic correction for enzyme instability (k ctrl > 0, Fig. 20F) can be performed in step 4 of this protocol by accounting for nonlinearity in the uninhibited control in the secondary k obs plot (Fig. 20G). Alternatively, proceed to Alternative Data Analysis Protocol 4Bii to correct for enzyme instability (v0ctrl > vt′ctrl) by normalization of the enzyme activity vt′/vt′ctrl (Fig. 20H and 20I).
2.Fit vt′ against preincubation time t′ to obtain k obs.
Fit the mean and standard deviation of vt′ against preincubation time t′ (Fig. 20C/F) for each inhibitor concentration to bounded exponential decay Equation VI (Fig. 18D). Constrain initial velocity vi to a shared value to obtain observed reaction rate k obs (in s−1) from initial velocity vi (Y-intercept) to full inactivation (vs = 0 or value in fully inhibited control).
\begin{equation} {{\rm{v}}_{{\rm{t^\prime}} }} = {\rm{v}}0^{{\rm{ctrl}}}{e^{ - {k{{\rm{obs}}}}{\rm{t^\prime}} }} \end{equation}
Equation VI for nonlinear regression of exponential one-phase decay equation Y = (Y0-Plateau)EXP(-kX) + Plateau with Y = preincubation time–dependent product formation velocity vt′ (in AU/s), X = preincubation time t′ (in s), and Plateau = final velocity vs = 0 or vs in fully inhibited control (in AU/s) to find Y0 = Y-intercept = initial velocity vi = uninhibited velocity v0ctrl (in AU/s, shared value) and k = observed reaction rate k obs (in s−1).
3.Plot k obs against [I].
Plot the mean and standard deviation of k obs (in s−1) on the Y-axis against inhibitor concentration (in M) during preincubation (before addition of substrate) on the X-axis (Fig. 20D/G). The plot of k obs against inhibitor concentration [I] is linear for one-step irreversible inhibitors and for two-step irreversible inhibitors at non-saturating inhibitor concentrations ([I] << 0.1KI).
4.Fit k obs against [I] to obtain k chem.
Fit k obs against inhibitor concentration during preincubation (in M) to Equation XVIII to obtain inhibitor potency k chem (in M−1s−1) from the linear slope. Constrain Y-intercept k ctrl = k obs of the uninhibited control (Fig. 20G). Inhibitor potency k chem does not have to be corrected for substrate competition because preincubation is conducted in absence of competing substrate. Calculate k inact/KI (in M−1s−1) for two-step irreversible inhibitors at non-saturating inhibitor concentrations ([I] ≤ 0.1KI) with propagation of error with Sample Calculation 9.
\begin{equation} {k_{{\rm{obs}}}} = {k_{{\rm{ctrl}}}} + {k_{{\rm{chem}}}}\left[ {\rm{I}} \right] \end{equation}
Equation XVIII for nonlinear regression of straight line Y = YIntercept + Slope*X with Y = observed reaction rate k obs (in s−1) and X = inhibitor concentration during preincubation (in M) to find YIntercept = rate of nonlinearity in uninhibited control k ctrl (in s−1) and Slope = inactivation rate constant k chem (in M−1s−1).
5.Optional : Validate experimental kinetic parameters with kinetic simulations.
Proceed to Kinetic Simulations 1 to compare the experimental read-out to the product formation simulated with scripts KinVol and KinVolDeg (using experimental rate constant k chem = k 3), to confirm that the calculated kinetic constants are in accordance with the experimental data.
Basic Protocol 20: One-Step Irreversible Covalent Inhibition
Processing of experimental data obtained with Basic Protocol IV that has been processed according to Basic Data Analysis Protocol 4 for one-step irreversible covalent inhibitors and two-step irreversible inhibitors at non-saturating inhibitor concentrations ([I] ≤ 0.1KI).
1.Plot vt′ against preincubation time t′ for each inhibitor concentration.
Plot the mean and standard deviation of vt′ (in AU/s) on the Y-axis against preincubation time t′ (in s) on the X-axis for each inhibitor concentration and the uninhibited control (Fig. 20C). Validate that inhibitor concentrations are not too high: inhibition should be less than 100% at the shortest t′ for at least six inhibitor concentrations.
2.Normalize vt′ to obtain vt′/vctrl.
Normalize vt′ (in AU/s) of each inhibitor concentration and the controls to lowest value = 0 (or full inhibition control) and highest value = uninhibited product formation vt′ctrl (in AU/s) to obtain normalized enzyme activity vt′/vctrl (Fig. 20H). Perform this correction separately for each preincubation time.
3.Plot and fit vt′/vctrl against preincubation time t′ to obtain k obs.
Plot the mean and standard deviation of vt′/vctrl on the Y-axis against preincubation time t′ (in s) on the X-axis (Fig. 20H). Fit to exponential decay Equation XVI to obtain k obs (in s−1) from initial velocity vi/v0ctrl (shared value) to full inactivation (Plateau = 0).
\begin{equation} \left( {\frac{{{{\rm{v}}{{\rm{t^\prime}} }}}}{{{\rm{v}}{{\rm{t^\prime}} }^{{\rm{ctrl}}}}}} \right) = {e^{ - {k_{{\rm{obs}}}}{\rm{t^\prime}} }} \end{equation}
Equation XVI for nonlinear regression of exponential one-phase decay equation Y = (Y0-Plateau)EXP(-kX) + Plateau with Y = normalized preincubation time–dependent product formation velocity vt′/vctrl (unitless), X = preincubation time t′ (in s), Plateau = normalized final velocity vs/vsctrl = 0 (unitless), and Y0 = Y-intercept = normalized initial velocity vi/v0ctrl = 1 (unitless) to find k = observed reaction rate k obs (in s−1).
4.Plot k obs against [I].
Plot the mean and standard deviation of k obs (in s−1) on the Y-axis against inhibitor concentration (in M) during preincubation (before addition of substrate) on the X-axis (Fig. 20I). The plot of k obs against inhibitor concentration [I] is linear for one-step irreversible inhibitors and for two-step irreversible inhibitors at non-saturating inhibitor concentrations ([I] << 0.1KI).
5.Fit k obs against [I] to obtain k chem.
Fit k obs against inhibitor concentration during preincubation to Equation XIX to obtain inhibitor potency k chem (in M−1s−1) from the linear slope (Fig. 20I). Do not correct for enzyme instability (k ctrl > 0), as this correction has already been performed by normalizing vt′ to vt′/vctrl in step 2 of this protocol. Inhibitor potency k chem does not have to be corrected for substrate competition because preincubation is conducted in absence of competing substrate. Calculate k inact/KI (in M−1s−1) for two-step irreversible inhibitors at non-saturating inhibitor concentrations ([I] ≤ 0.1KI) with propagation of error with Sample Calculation 9. Alternatively, inhibitor potency k chem (in M−1s−1) or k inact/KI (in M−1s−1) can be directly calculated from a single k obs (s−1) and [I] (in M) with Sample Calculation 10.
\begin{equation} {k_{{\rm{obs}}}} = {k_{{\rm{chem}}}}\left[ {\rm{I}} \right] \end{equation}
Equation XIX for nonlinear regression of straight line Y = YIntercept + Slope*X with Y = observed reaction rate k obs (in s−1), X = inhibitor concentration during preincubation (in M), and YIntercept = 0 (in s−1) to find Slope = inactivation rate constant k chem (in M−1s−1).
6.Optional : Validate experimental kinetic parameters with kinetic simulations by proceeding to Basic Data Analysis Protocol 4Bi step 5.
SAMPLE CALCULATIONS
The fits as obtained in the basic protocols described above still have to be converted into inhibition parameters. These are fairly straightforward linear calculations and can be performed with more basic software like Microsoft Excel. For each equation, the full right side of the equal sign is known, so it becomes a linear calculation to obtain the parameter on the left side of it.
All calculations used are listed here in order of appearance in the manuscript. We have outlined the key assumptions and a little background on the used variables for improved readability and direct applicability after following the basic protocols.
Materials
Experimental/fitted values found in Data Analysis Protocols 1-4 Software to perform linear calculations (e.g., EXCEL)
Sample Calculation 1. Calculate KI from KIapp
Apparent inactivation constant KIapp (in M) found in Data Analysis Protocols (1A or 1D) for competitive two-step irreversible inhibitors is corrected for substrate competition to obtain inactivation constant KI (in M), with propagation of error. Use substrate concentration [S] (in M) after reaction initiation and KM (in M) as determined for these specific assay conditions (buffer, temperature, enzyme, substrate). Proceed to Sample Calculation 2 to calculate k inact/KI. \begin{eqnarray*} {{\rm{K}}{\rm{I}}} &&= \frac{{{{\rm{K}}{\rm{I}}}^{{\rm{app}}}}}{{\left( {1 + \frac{{\left[ {\rm{S}} \right]}}{{{{\rm{K}}{\rm{M}}}}}} \right)}};with\\ &&{{\rm{\sigma }}{{{\rm{K}}{\rm{I}}}}} = \sqrt {{{\left( {\frac{1}{{1 + \frac{{\left[ {\rm{S}} \right]}}{{{{\rm{K}}{\rm{M}}}}}}}} \right)}^2}{{\rm{\sigma }}{{{\rm{K}}{\rm{I}}}^{{\rm{app}}}}}^2 + {{\left( { - \frac{{{{\rm{K}}{\rm{I}}}^{{\rm{app}}};{{\rm{K}}{\rm{M}}}}}{{{{\left( {{{\rm{K}}{\rm{M}}} + \left[ {\rm{S}} \right]} \right)}^2}}}} \right)}^2}{{\rm{\sigma }}{\left[ {\rm{S}} \right]}}^2 + {{\left( {\frac{{{{\rm{K}}{\rm{I}}}^{{\rm{app}}};\left[ {\rm{S}} \right]}}{{{{\left( {\left[ {\rm{S}} \right] + {{\rm{K}}{\rm{M}}}} \right)}^2}}}} \right)}^2}{{\rm{\sigma }}{{{\rm{K}}{\rm{M}}}}}^2} \end{eqnarray*}
Sample Calculation 2. Calculate kinact/KI from kinact and KI
Irreversible covalent inhibitor potency k inact/KI (in M−1s−1) is calculated from k inact (in s−1) and KI (in M) values found in Data Analysis Protocols (1A, 1D, 2, 3Ai, 3Aii, 4Ai or 4Aii) and Sample Calculation 1 for two-step irreversible inhibitors, with propagation of error. \begin{equation*} \left( {\frac{{{k_{{\rm{inact}}}}}}{{{{\rm{K}}{\rm{I}}}}}} \right); = \frac{{{k{{\rm{inact}}}}}}{{{{\rm{K}}{\rm{I}}}}};;with;;{{\rm{\sigma }}{\frac{{{k_{{\rm{inact}}}}}}{{{{\rm{K}}{\rm{I}}}}}}} = \left( {\frac{{{k{{\rm{inact}}}}}}{{{{\rm{K}}{\rm{I}}}}}} \right)\sqrt {{{\left( {\frac{{{{\rm{\sigma }}{{k_{{\rm{inact}}}}}}}}{{{k_{{\rm{inact}}}}}}} \right)}^2} + {{\left( {\frac{{{{\rm{\sigma }}{{{\rm{K}}{\rm{I}}}}}}}{{{{\rm{K}}_{\rm{I}}}}}} \right)}^2}} \end{equation*}
Sample Calculation 3. Calculate Ki from Kiapp
Apparent inhibition constant Kiapp (in M) found in Data Analysis Protocols (1A, 1C, 3Ai, 3Aii or 3C) for competitive two-step (ir)reversible inhibitors is corrected for substrate competition (Cheng & Prusoff, 1973) to obtain inhibition constant Ki (in M) for the initial noncovalent equilibrium. Use substrate concentration [S] (in M) after reaction initiation and KM (in M) as determined for these specific assay conditions (buffer, temperature, enzyme, substrate). Inhibition constant Ki approximates inactivation constant KI for two-step irreversible inhibitors if covalent bond formation is rate-limiting (rapid equilibrium assumption). \begin{eqnarray*} {{\rm{K}}{\rm{i}}} &&= \frac{{{{\rm{K}}{\rm{i}}}^{{\rm{app}}}}}{{\left( {1 + \frac{{\left[ {\rm{S}} \right]}}{{{{\rm{K}}{\rm{M}}}}}} \right)}};with\\ &&{{\rm{\sigma }}{{{\rm{K}}{\rm{i}}}}} = \sqrt {{{\left( {\frac{1}{{1 + \frac{{\left[ {\rm{S}} \right]}}{{{{\rm{K}}{\rm{M}}}}}}}} \right)}^2}{{\rm{\sigma }}{{{\rm{K}}{\rm{i}}}^{{\rm{app}}}}}^2 + {{\left( { - \frac{{{{\rm{K}}{\rm{i}}}^{{\rm{app}}};{{\rm{K}}{\rm{M}}}}}{{{{\left( {{{\rm{K}}{\rm{M}}} + \left[ {\rm{S}} \right]} \right)}^2}}}} \right)}^2}{{\rm{\sigma }}{\left[ {\rm{S}} \right]}}^2 + {{\left( {\frac{{{{\rm{K}}{\rm{i}}}^{{\rm{app}}};\left[ {\rm{S}} \right]}}{{{{\left( {\left[ {\rm{S}} \right] + {{\rm{K}}{\rm{M}}}} \right)}^2}}}} \right)}^2}{{\rm{\sigma }}{{{\rm{K}}{\rm{M}}}}}^2} \end{eqnarray*}
Sample Calculation 4. Calculate kchem from kchemapp
Apparent inhibitor potency k chemapp (in M−1s−1) found in Data Analysis Protocol 1B for competitive one-step irreversible inhibitors is corrected for substrate competition to obtain inhibition potency k chem (in M−1s−1) with propagation of error. Use substrate concentration [S] (in M) after reaction initiation and KM (in M) as determined for these specific assay conditions (buffer, temperature, enzyme, substrate). \begin{eqnarray*} {k_{{\rm{chem}}}} &&= k_{{\rm{chem}}}^{{\rm{app}}}\left( {1 + \frac{{\left[ {\rm{S}} \right]}}{{{{\rm{K}}{\rm{M}}}}}} \right);;with\\ &&{{\rm{\sigma }}{{k_{{\rm{chem}}}}}} = \sqrt {{{\left( {1 + \frac{{\left[ {\rm{S}} \right]}}{{{{\rm{K}}{\rm{M}}}}}} \right)}^2}{{\rm{\sigma }}{k_{{\rm{chem}}}^{{\rm{app}}}}}^2 + {{\left( {\frac{{k_{{\rm{chem}}}^{{\rm{app}}};}}{{{{\rm{K}}{\rm{M}}}}}} \right)}^2}{{\rm{\sigma }}{\left[ {\rm{S}} \right]}}^2 + {{\left( { - \frac{{k_{{\rm{chem}}}^{{\rm{app}}};\left[ {\rm{S}} \right]}}{{{{\rm{K}}{\rm{M}}}^2}}} \right)}^2}{{\rm{\sigma }}{{{\rm{K}}_{\rm{M}}}}}^2} \end{eqnarray*}
Sample Calculation 5. Calculate kinact/KIapp from kchemapp
The linear slope k chemapp (in M−1s−1) found in Data Analysis Protocol 1B for two-step irreversible inhibitors equals k inact/KIapp when all inhibitor concentrations are non-saturating ([I] ≤ 0.1Kiapp). It is not possible to obtain individual values of k inact and KI from a linear graph, but it is possible to estimate the upper and lower limits: KIapp is much larger than the highest inhibitor concentration if this concentration is non-saturating (KIapp >> [I]max). An unchanged slope upon constraining the Y-intercept k ctrl (step 5) to the experimental value for the uninhibited control validates that all inhibitor concentrations are non-saturating (Fig. 3F) rather than saturating (Fig. 3G). Proceed to Sample Calculation 6 to calculate k inact/KI. \begin{equation*} k_{{\rm{chem}}}^{{\rm{app}}} = \left( {\frac{{{k_{{\rm{inact}}}}}}{{{{\rm{K}}_{\rm{I}}}^{{\rm{app}}}}}} \right) \end{equation*}
Sample Calculation 6. Calculate kinact/KI from kinact/KIapp
Apparent inactivation potency k inact/KIapp (in M−1s−1) found in Data Analysis Protocols (1A or 1D) or calculated in Sample Calculation 5 for competitive two-step irreversible inhibitors is corrected for substrate competition to obtain k inact/KI (in M) with propagation of error. Use substrate concentration [S] (in M) after reaction initiation and KM (in M) as determined for these specific assay conditions (buffer, temperature, enzyme, substrate). \begin{eqnarray*} \frac{{{k_{{\rm{inact}}}}}}{{{{\rm{K}}{\rm{I}}}}} &&= \left( {\frac{{{k{{\rm{inact}}}}}}{{{{\rm{K}}{\rm{I}}}^{{\rm{app}}}}}} \right)\left( {1 + \frac{{\left[ {\rm{S}} \right]}}{{{{\rm{K}}{\rm{M}}}}}} \right);;with\\ &&{{\rm{\sigma }}{\frac{{{k{{\rm{inact}}}}}}{{{{\rm{K}}{\rm{I}}}}}}} = \sqrt {{{\left( {1 + \frac{{\left[ {\rm{S}} \right]}}{{{{\rm{K}}{\rm{M}}}}}} \right)}^2}{{\rm{\sigma }}{\left( {\frac{{{k{{\rm{inact}}}}}}{{{{\rm{K}}{\rm{I}}}^{{\rm{app}}}}}} \right)}}^2 + {{\left( {\frac{{\left( {\frac{{{k{{\rm{inact}}}}}}{{{{\rm{K}}{\rm{I}}}^{{\rm{app}}}}}} \right);}}{{{{\rm{K}}{\rm{M}}}}}} \right)}^2}{{\rm{\sigma }}{\left[ {\rm{S}} \right]}}^2 + {{\left( { - \frac{{\left( {\frac{{{k{{\rm{inact}}}}}}{{{{\rm{K}}{\rm{I}}}^{{\rm{app}}}}}} \right);\left[ {\rm{S}} \right]}}{{{{\rm{K}}{\rm{M}}}^2}}} \right)}^2}{{\rm{\sigma }}{{{\rm{K}}{\rm{M}}}}}^2} \end{eqnarray*}
Sample Calculation 7. Calculate Ki* from Ki*app
Apparent steady-state inhibition constant Kiapp (in M) found in Data Analysis Protocols (1C or 3C) for competitive two-step reversible covalent inhibitors is corrected for substrate competition to obtain steady-state inhibition constant Ki (in M). Use substrate concentration [S] (in M) after reaction initiation and KM (in M) as determined for these specific assay conditions (buffer, temperature, enzyme, substrate). \begin{eqnarray*} {\rm{K}}{\rm{i}}^{\rm{*}} &&= \frac{{{\rm{K}}{\rm{i}}^{{\rm{app}}}}}{{\left( {1 + \frac{{\left[ {\rm{S}} \right]}}{{{{\rm{K}}{\rm{M}}}}}} \right)}};with\\ &&{{\rm{\sigma }}{{\rm{K}}_{\rm{i}}^{\rm{}}}} = \sqrt {{{\left( {\frac{1}{{1 + \frac{{\left[ {\rm{S}} \right]}}{{{{\rm{K}}{\rm{M}}}}}}}} \right)}^2}{{\rm{\sigma }}{{\rm{K}}{\rm{i}}^{{\rm{*app}}}}}^2 + {{\left( { - \frac{{{\rm{K}}{\rm{i}}^{{\rm{*app}}}{\rm{;}}{{\rm{K}}{\rm{M}}}}}{{{{\left( {{{\rm{K}}{\rm{M}}} + \left[ {\rm{S}} \right]} \right)}^2}}}} \right)}^2}{{\rm{\sigma }}{\left[ {\rm{S}} \right]}}^2 + {{\left( {\frac{{{\rm{K}}{\rm{i}}^{{\rm{app}}};\left[ {\rm{S}} \right]}}{{{{\left( {\left[ {\rm{S}} \right] + {{\rm{K}}{\rm{M}}}} \right)}^2}}}} \right)}^2}{{\rm{\sigma }}{{{\rm{K}}_{\rm{M}}}}}^2} \end{eqnarray}
Sample Calculation 8. Calculate Ki* from Ki, k5, and k6
Steady-state inhibition constant Ki* (in M) of two-step reversible inhibitors can be calculated from experimental values of Ki (in M), k 5 (in s−1), and k 6 (in s−1) found with Data Analysis Protocols 1C or 3C , and Sample Calculation 3. Reliable (relatively) small k 6-values can only be obtained with more sensitive methods such as rapid dilution assays (Copeland, 2013e; Copeland et al., 2011). The uninhibited control must be strictly linear (k ctrl = 0) for values found with Data Analysis Protocol 1C. This calculation is not the preferred method to obtain Ki* due to its sensitivity to (experimental) errors in k 6 and contribution of k ctrl: values obtained in Data Analysis Protocol 1C or 3C and Sample Calculation 7 should generally be considered as more reliable. \begin{eqnarray*} {\rm{K}}{\rm{i}}^{\rm{*}} &&= \frac{{{{\rm{K}}{\rm{i}}}}}{{\left( {1 + \frac{{{k_5}}}{{{k_6}}}} \right)}};with\\ &&{{\rm{\sigma }}{{\rm{K}}{\rm{i}}^{\rm{}}}} = \sqrt {{{\left( {\frac{1}{{1 + \frac{{{k_5}}}{{{k_6}}}}}} \right)}^2}{{\rm{\sigma }}{{{\rm{K}}{\rm{i}}}}}^2 + {{\left( { - \frac{{{{\rm{K}}{\rm{i}}};{k_6}}}{{{{\left( {{k_6} + {k_5}} \right)}^2}}}} \right)}^2}{{\rm{\sigma }}{{k_5}}}^2 + {{\left( {\frac{{{{\rm{K}}{\rm{i}}};{k_5}}}{{{{\left( {{k_5} + {k_6}} \right)}^2}}}} \right)}^2}{{\rm{\sigma }}{{k_6}}}^2} \end{eqnarray}
Sample Calculation 9. Calculate kinact/KI from kchem
The linear slope k chem (in M−1s−1) found in Data Analysis Protocols (3Bi, 3Bii, 4Bi or 4Bii) for two-step irreversible inhibitors equals k inact/KI when all inhibitor concentrations are non-saturating ([I] ≤ 0.1Ki). It is not possible to obtain individual values of k inact and KI from a linear graph, but it is possible to estimate the upper and lower limits: KI is much larger than the highest inhibitor concentration if this concentration is non-saturating (KI >> [I]max). An unchanged slope upon constraining the Y-intercept k ctrl to the experimental value for the uninhibited control in step 4 of Basic Data Analysis Protocols (3Bi and 4Bi) validates that all inhibitor concentrations are non-saturating (Fig. 3F) rather than saturating (Fig. 3G). \begin{equation*} {k_{{\rm{chem}}}} = \left( {\frac{{{k_{{\rm{inact}}}}}}{{{{\rm{K}}_{\rm{I}}}}}} \right) \end{equation*}
Sample Calculation 10. Calculate kchem or kinact/KI from kobs and [I]
Divide the k obs-value (in s−1) obtained in Alternative Data Analysis Protocols (3Bii or 4Bii) by its corresponding inhibitor concentration (in M) to calculate irreversible inhibitor potency k chem (in M−1s−1) or k inact/KI (in M−1s−1). This calculation is only accurate for normalized k obs values (unaffected by contribution of k ctrl), in absence of competing substrate, and (only applicable for two-step irreversible inhibitors) at non-saturating inhibitor concentration. \begin{equation*} {k_{{\rm{chem}}}} = \frac{{{k_{{\rm{obs}}}}}}{{\left[ {\rm{I}} \right]}} \end{equation*} \begin{equation*} \left( {\frac{{{k_{{\rm{inact}}}}}}{{{{\rm{K}}{\rm{I}}}}}} \right) = \frac{{{k{{\rm{obs}}}}}}{{\left[ {\rm{I}} \right]}} \end{equation*}
KINETIC SIMULATIONS
The figures illustrating the basic protocols are generated using kinetic simulation scripts. These scripts are available online (https://tinyurl.com/kineticsimulations) and can be used to validate the obtained kinetic parameters or help in optimizing your assay. On a more educational level, these scripts can show what your assay result could look like when using wildly different parameters to obtain more insight into how these affect your assay.
Materials
Kinetic Simulation Script (https://tinyurl.com/kineticsimulations) Software to open csv file (e.g., EXCEL) Data fitting software (e.g., GraphPad Prism) Experimental values found in Data Analysis Protocols 1-4
Kinetic Simulation 1. Validation of experimental values
Perform kinetic simulations to validate that calculated kinetic parameters are in accordance with experimental RAW data. A tutorial on how to perform kinetic simulations can be found on the website of our kinetic simulation scripts. Estimate microscopic rate constants from reported (literature) values, or use association rate constants k 1 = k 3 = 106-109 M−1s−1 (rapid noncovalent association) to calculate the dissociation rate constants from the experimental equilibrium constants: k 4 = Ki× k 3 (Table S2 in Supporting Information) and k 2 = (KM× k 1)-k cat (Table S3 in Supporting Information). Ideally, also simulate the HTS reaction conditions to validate that the calculated kinetic constants give rise to the experimental inhibition/IC50 (Pollard & De La Cruz, 2013).
Kinetic Simulation 2. Rational design of validation assays
Perform kinetic simulations with the calculated kinetic parameters to rationalize assay conditions for subsequent validation assays such as the minimum/maximum (pre)incubation times for reversibility assays or MS-detection of the covalent adduct (equations can be found in the Supporting Information).
COMMENTARY
Background Information
The background of covalent inhibition kinetics and critical parameters for enzyme activity assays can be found in the Strategic Planning section. It is recommended to refer to this section before setting up your kinetic inhibition experiments as well as the core references by Copeland (Copeland, 2000, 2013e) to get a general background on enzyme activity assays. We would like to reiterate that good experimental performance is essential for obtaining reliable parameters for your covalent inhibitor.
Our kinetic simulation scripts can help validate the found values by ‘rerunning’ the experiment without human error or experimental artifacts. Not only will this give insight into the reliability of your assay, but it can also help to improve the assay setup and can show what wildly different values of concentrations would do for the readout. In fact, figures in this manuscript have been created this way, and can as such be reproduced. Keep in mind that these are simulations, and real-life examples will always deviate due to machine artifacts or pipetting errors. Nevertheless, with a working activity assay and these instructions in hand, adequate analysis of covalent inhibitors should be very feasible.
Troubleshooting
Like with any experimental method, our described methods will also require the necessary optimization. Since data analysis depends heavily on the experimental input, it is very important to optimize assay conditions, rather than trying to apply data corrections, to obtain reliable kinetic parameters. As the assay conditions will vary widely, depending on the enzyme used (Bisswanger, 2014), we can only give general pointers on the optimization of the assay conditions (Table 3). Luckily, many model substrates come with a satisfactory user manual or are described in extensive methods papers (e.g., (Dharadhar et al., 2019; Janssen et al., 2019)). These resources generally state reagents required for the reaction (e.g., fresh reducing agent, for cysteine-based catalysis) or additives that stabilize the readout (such as BSA or Tween-20, to prevent aspecific aggregation). The control for full inhibition of (catalytic) cysteines is typically a thiol-alkylating reagent such as iodoacetamide (IAc) or N-methylmaleimide (NEM), or a known inhibitor.
| Problem | Possible cause | Solutions |
|---|---|---|
| Difference positive and negative control is not significant (poor Z′-score) | Enzyme is not active (enough) |
Increase [E] (not always possible with very potent inhibitors) Increase [S] to increase absolute maximum signal Optimize buffer components Switch to a substrate that is processed faster Activate enzyme with fresh reagents (e.g., DTT, ATP) in single-use aliquots Minimize freeze/thaw cycles |
| Signal product is not significant compared to substrate |
Change fluorophore/read-out Optimize buffer components |
|
| Negative control or inhibitor does not inhibit |
Change to reported (specific) inhibitor Use thiol-alkylating reagent (e.g., NEM, IAc) for cysteines Use no-enzyme as negative control Increase concentration of inhibitor Make fresh dilution/aliquots of inhibitor solution |
|
| DMSO in positive control acts as inhibitor |
Validate: compare enzyme activity with/without DMSO Reduce DMSO to max. 1% of final solution |
|
| Machine settings/sensitivity |
Check if [P] is within the sensitivity range of used machine Optimize gain settings for [P] = 0–20% [S]0 Check if correct wavelengths/settings are selected |
|
| Pipetting error |
Frequently replace pipette tips to avoid contamination of positive control with inhibitor (from negative control) Avoid well-to-well contamination by using an automated dispenser |
|
| Nonlinear uninhibited product formation curve Fctrl | Substrate depletion ([P]t > 0.1[S]0) |
Decrease [E] Increase [S] Shorter incubation time |
| Spontaneous inactivation of enzyme (kdeg > 0) |
Optimize buffer conditions for stability Use non-binding surface plates Shorter incubation time |
|
| Drift/evaporation |
Cover/seal plate with optical clear cover Shorter incubation time |
|
| Pre-steady state kinetics (lag phase) |
Increase [S] to reach E + S <-> ES equilibrium faster Preincubate enzyme with reducing agent/ATP |
|
| Solution is not homogeneous | Introduce mixing step before addition of final component | |
| Fluorescence bleaching/quenching |
Optimize excitation conditions (e.g., lower no. of flashes) Longer measurement intervals/less measurements |
|
| Linear inhibited progress curve Ft | Inhibition is not time-dependent (or kobs is too slow) |
Longer (pre)incubation time (t > 0.1t½) Increase [I] Reduce [S] to decrease competition Activate enzyme with fresh reagents (e.g., DTT, ATP) Validate with different enzyme batch/construct |
| F0 is not constant | Delay between enzyme addition and read-out |
Reduce [E] (less substrate conversion during delay) Correcting t = 0 for actual time after addition Use injector in plate reader Validate row effect: change lay-out of plate (first well has higher F0 than last well, but containing same components) and reduce number of samples in one measurement. |
| Fluorescence interference inhibitor |
Validate: check F0 for inhibitor (no substrate and enzyme), substrate (no enzyme) and substrate and inhibitor (no enzyme) Exclude high [I] Background subtraction (subtract values substrate/inhibitor without enzyme from enzyme/substrate/inhibitor signal) |
|
| Pipetting error substrate |
Check for bubbles when pipetting Use low-binding tips |
|
| Full initial inhibition for all [I] (vi = 0) | Noncovalent affinity is too potent ([I] >> Kiapp) |
Reduce [I] Higher [S] to increase competition (higher Kiapp) Use method based on covalency (Method IV or direct detection) |
| kobs is too fast for detection/resolvable range (inhibition is not slow-binding) |
Shorter minimal (pre)incubation time Higher [S] to increase competition (slower kobs) Reduce [I] (slower kobs) |
|
| kobs values are low compared to uninhibited control kctrl | Enzyme is unstable (high kctrl) |
Optimize assay conditions to improve linearity of uninhibited control (lower kctrl) Use preincubation protocol (Method III & IV): higher kobs without competition |
| Enzyme is not reactive (low kobs) |
Optimize buffer conditions to increase enzyme reactivity Add (fresh) reagents (e.g., DTT, ATP) in single-use aliquots Validate with different enzyme batch/construct Too many freeze/thaw cycles |
|
| Low inhibitor concentration ([I] << Kiapp) |
Decrease [S] to reduce competition Increase [I] Use preincubation protocol (Method III & IV): higher kobs without competition |
|
| Slow reaction kobs |
Reduce [S] (less competition) Longer (pre)incubation time (t > 0.1t½) Use preincubation protocol (Method III & IV): higher kobs without competition Optimize buffer conditions to increase enzyme reactivity |
|
| kobs vs [I] is linear | Inhibitor has 1-step binding mode |
Validate: Y-intercept = kctrl in kobs vs [I] plot Validate: vi = v0ctrl in [P]t vs t or vt′ vs t′ plots Increase [I] to exclude 2-step [I] << KIapp Decrease [S] to exclude 2-step [I] << KIapp |
| 2-step IRREV inhibitor is non-saturating ([I] << KIapp) |
Validate: Y-intercept = kctrl in kobs vs [I] plot Validate: vi = v0ctrl in [P]t vs t or vt′ vs t′ plots Fit kobs vs [I] to linear function for combined value kinact/KI Increase [I] Decrease [S] to reduce competition (lower KIapp) Use preincubation protocol (Method III & IV): no competition |
|
| 2-step IRREV inhibitor is saturating ([I] >> KIapp) |
Validate: Y-intercept > kctrl in kobs vs [I] plot Validate: vi < v0ctrl in [P]t vs t or vt′ vs t′ plots Decrease [I] Increase [S] to increase competition (higher KIapp) |
|
| kobs decreases with increasing [I] | Inhibitor concentration beyond resolvable range: noncovalent affinity is too potent ([I] >> Kiapp) |
Optimize [I] range (vi = 0.1-0.9×vctrl) Increase [S] (increase competition to increase Kiapp) Exclude unlikely values from fit |
| Incorrect formula to calculate kobs | Validate if correct equation is used to determine kobs; reversible covalent/irreversible covalent, one-step/two-step etc. | |
As the assay performance is essential to get reliable fits, we recommend focusing on potential experimental problems before looking into issues with fitting. A great guide for general assay optimization can be found at the National Center for Advancing Translational Sciences (Assay Guidance Manual [Internet], 2004-2021; see Internet Resources). Here, we have supplied a comprehensive troubleshooting table with potential solutions that deal with various issues causing a troublesome readout. For the top half of the table, these solutions are generally related to the assay conditions and can generally be executed in the optimization stage.
The latter half of the table is more geared towards after the data analysis of an initial experiment. The problems and accompanying solutions deal more with the experimental setup: how much inhibitor or substrate one needs to add becomes more apparent after these first data points. Some solutions, like changing inhibitor or substrate concentrations, can be simulated with our set of interactive kinetic simulation scripts. For better understanding and help in optimizing, we recommend simulating these conditions with our scripts to see what would happen when changing the concentrations.
Abbreviations and Symbols
Abbreviations
| ATP | Adenosine Triphosphate |
| AU | Arbitrary Units |
| CYP450 | Cytochrome P450 |
| IAc | Iodoacetamide |
| IRREV | Irreversible |
| MS | Mass Spectrometry |
| NBS | Non-binding Surface |
| NMR | Nuclear Magnetic Resonance |
| M | Concentration in mol/L |
| NEM | N-ethylmaleimide |
| REV | Reversible |
| SAR | Structure-Activity Relationship |
| TCI | Targeted Covalent Inhibition |
| TDI | Time-Dependent Inactivation |
| PK-PD | Pharmacokinetics-Pharmacodynamics |
| E | unbound enzyme |
| I | unbound inhibitor |
| EI | noncovalent enzyme-inhibitor complex |
| EI* | covalent enzyme-inhibitor adduct |
| S | unbound substrate |
| ES | noncovalent enzyme-substrate complex |
| P | (detectable) product |
Symbols
| k1 | Second-order association rate constant for E + S <-> ES reaction (in M−1s−1) |
| k2 | First-order dissociation rate constant for E + S <-> ES equilibrium (in s−1) |
| k3 | Second-order association rate constant for E + I <-> EI reaction (in M−1s−1) |
| k4 | First-order dissociation rate constant for E + I <-> EI equilibrium (in s−1) |
| k5 | First-order association rate constant for EI → EI* reaction (in s−1) |
| k6 | First-order dissociation rate constant for EI <-> EI* equilibrium (in s−1) |
| Ft | Detected signal reflecting product formation in presence of inhibitor after incubation t (in AU) |
| Fctrl | Detected signal reflecting product formation in the uninhibited control (in AU) |
| F0 | Background signal at reaction initiation (in AU) |
| rP | Product coefficient for detected signal per formed product (in AU/M) |
| vi | Initial product formation velocity in presence of inhibitor (in AU/s) |
| vs | Steady-state/final product formation velocity in presence of inhibitor (in AU/s) |
| vt′ | Product formation velocity after preincubation t′ (in AU/s) |
| vctrl | Product formation velocity in the uninhibited control (in AU/s) |
| vt′ctrl | Product formation velocity in the uninhibited control after preincubation t′ (in AU/s) |
| v0ctrl | Product formation velocity in the uninhibited control without preincubation: t′=0 (in AU/s) |
| t | Incubation time after onset of product formation (in s) |
| t′ | Preincubation time after onset of enzyme inhibition (in s) |
| t½ | Half-life for reaction progress (in s). |
| t½diss | Half-life for dissociation reaction (in s) |
| τ | Target residence time (in s) |
| kobs | Observed reaction rate constant (in s−1) |
| kmax | Maximum reaction rate constant at saturating inhibitor concentration for 2-step inhibition (in s−1) |
| kinact | Inactivation rate constant for EI → EI* at saturating inhibitor concentration for 2-step irreversible inhibition (in s−1) |
| kctrl | Reaction rate constant for nonlinearity or loss of enzyme activity in uninhibited control (in s−1) |
| kdegE | Enzyme degradation rate constant for E → Edeg (in s−1) |
| kcat | Product formation rate constant for ES → E + P (in s−1) at saturating substrate concentration |
| ksub | Reaction rate constant for E + S → E + P (in M−1s−1) (= kcat/KM if [S] << 0.1KM) |
| kchem | Reaction rate constant for E + I → EI* of 1-step irreversible inhibitors (in M−1s−1) |
| koff | Overall dissociation rate constant from bound to unbound enzyme EI + EI* → E + I (in s−1) |
| Ki | Inhibition/dissociation constant (in M) for noncovalent E + I <-> EI equilibrium of two-step inhibition |
| Kiapp | Apparent noncovalent inhibition constant (in M): with substrate competition |
| Ki* | Steady-state inhibition constant (in M) for E + I <-> EI + EI* equilibrium of two-step reversible inhibition |
| Ki*app | Apparent steady-state inhibition constant (in M): with substrate competition |
| KI | Inactivation constant for E + I → EI* (in M) of two-step irreversible inhibition |
| KIapp | Apparent inactivation constant (in M): with substrate competition |
| KM | Michaelis-Menten constant for E + S → E + P (in M) |
| kinact/KI | Inactivation efficiency: reaction rate constant for E + I → EI* of 2-step irreversible inhibitors (in M−1s−1) |
| IC50 | Inhibitor concentration resulting in half-maximum inhibition (in M) |
| IC50(t) | Inhibitor concentration resulting in half-maximum inhibition after incubation time t (in M) |
| [Etotal] | Combined total concentration of all enzyme species (Etotal = E + EI + EI* + ES + Edeg + EIdeg + EI*deg + ESdeg) |
| [E]0 | Unbound enzyme concentration at reaction initiation (before binding to inhibitor/substrate) |
| [I]0 | Unbound inhibitor concentration at onset of inhibition (before binding to enzyme) |
| [S]0 | Unbound substrate concentration at onset of product formation (before binding to enzyme) |
| [EI]eq | Noncovalent EI concentration at (steady-state) equilibrium |
| [X]0 | Concentration of component X at reaction initiation (before binding to other reaction components) |
| [X]t | Concentration of component X at incubation time t |
| [X]t′ | Concentration of component X at preincubation time t′ |
| Vt | Incubation reaction volume containing enzyme, inhibitor and substrate (Vt = Vt′ + Vsub) |
| Vt′ | Preincubation reaction volume containing enzyme and inhibitor |
| Vsub | Volume containing substrate |
Acknowledgments
This work was supported by the EU/EFPIA/OICR/McGill/KTH/Diamond Innovative Medicines Initiative 2 Joint Undertaking (EUbOPEN grant no. 875510). The authors would like to thank Dr. Anthe Janssen for proof reading. In memory of Prof. Dr. Huib Ovaa, his passion for science will always be an inspiration to us.
Author Contributions
Elma Mons : conceptualization, formal analysis, investigation, visualization, writing original draft, writing review and editing; Sander Roet : conceptualization, resources, software, writing review and editing; Robbert Kim : supervision, validation, writing original draft, writing review and editing; Monique Mulder : project administration, supervision, writing review and editing.
Conflict of Interest
The authors declare no conflict of interest.
Open Research
Data Availability Statement
The authors confirm that the data supporting the findings of this study are available within the article [and/or] its supplementary materials.
Supporting Information
| Filename | Description |
|---|---|
| cpz1419-sup-0001-SuppMat.pdf983.3 KB | Suppinfo |
Please note: The publisher is not responsible for the content or functionality of any supporting information supplied by the authors. Any queries (other than missing content) should be directed to the corresponding author for the article.
Literature Cited
- Abdeldayem, A., Raouf, Y. S., Constantinescu, S. N., Moriggl, R., & Gunning, P. T. (2020). Advances in covalent kinase inhibitors doi: 10.1039/C9CS00720B]. Chemical Society Reviews , 49(9), 2617–2687. doi: 10.1039/C9CS00720B.
- Acker, M. G., & Auld, D. S. (2014). Considerations for the design and reporting of enzyme assays in high-throughput screening applications. Perspectives in Science , 1(1), 56–73. doi: 10.1016/j.pisc.2013.12.001.
- Assay Guidance Manual (2004-2021). Eli Lilly & Company and the National Center for Advancing Translational Sciences. http://www.ncbi.nlm.nih.gov/books/NBK53196/.
- Auld, D. S., Inglese, J., & Dahlin, J. L. (2017). Assay Interference by Aggregation. In Assay Guidance Manual [Internet]. Eli Lilly & Company and the National Center for Advancing Translational Sciences. Available at https://www.ncbi.nlm.nih.gov/books/NBK442297/.
- Barf, T., & Kaptein, A. (2012). Irreversible protein kinase inhibitors: Balancing the benefits and risks. Journal of Medicinal Chemistry , 55(14), 6243–6262. doi: 10.1021/jm3003203.
- Bauer, R. A. (2015). Covalent inhibitors in drug discovery: From accidental discoveries to avoided liabilities and designed therapies. Drug Discovery Today , 20(9), 1061–1073. doi: 10.1016/j.drudis.2015.05.005.
- Bisswanger, H. (2014). Enzyme assays. Perspectives in Science , 1(1), 41–55. doi: 10.1016/j.pisc.2014.02.005.
- Bradshaw, J. M., McFarland, J. M., Paavilainen, V. O., Bisconte, A., Tam, D., Phan, V. T., … Taunton, J. (2015). Prolonged and tunable residence time using reversible covalent kinase inhibitors. Nature Chemical Biology , 11(7), 525–531. doi: 10.1038/nchembio.1817.
- Cheng, Y.-C., & Prusoff, W. H. (1973). Relationship between the inhibition constant (KI) and the concentration of inhibitor which causes 50 per cent inhibition (I50) of an enzymatic reaction. Biochemical Pharmacology , 22(23), 3099–3108. doi: 10.1016/0006-2952(73)90196-2.
- Copeland, R. A. (2000). ENZYMES: A Practical Introduction to Structure, Mechanism, and Data Analysis, Second Edition. John Wiley & Sons, Inc. doi: 10.1002/0471220639.
- Copeland, R. A. (2010). The dynamics of drug-target interactions: Drug-target residence time and its impact on efficacy and safety. Expert Opinion on Drug Discovery , 5(4), 305–310. doi: 10.1517/17460441003677725.
- Copeland, R. A. (2013a). APPENDIX 1 : Kinetics of Biochemical Reactions. In Evaluation of Enzyme Inhibitors in Drug Discovery: A Guide for Medicinal Chemists and Pharmacologists ( Second Edition, pp. 471–482). John Wiley & Sons, Inc. doi: 10.1002/9781118540398.app1.
- Copeland, R. A. (2013b). Chapter 6. Slow Binding Inhibitors. In Evaluation of Enzyme Inhibitors in Drug Discovery: A Guide for Medicinal Chemists and Pharmacologists ( Second Edition, pp. 203–244). John Wiley & Sons, Inc. doi: 10.1002/9781118540398.ch6.
- Copeland, R. A. (2013c). Chapter 7. Tight binding inhibition. In Evaluation of Enzyme Inhibitors in Drug Discovery: A Guide for Medicinal Chemists and Pharmacologists ( Second Edition, pp. 245–285). John Wiley & Sons, Inc. doi: 10.1002/9781118540398.ch7.
- Copeland, R. A. (2013d). Chapter 9. Irreversible Enzyme Inactivators. In Evaluation of Enzyme Inhibitors in Drug Discovery: A Guide for Medicinal Chemists and Pharmacologists ( Second Edition, pp. 345–382). John Wiley & Sons, Inc. doi: 10.1002/9781118540398.
- Copeland, R. A. (2013e). Evaluation of Enzyme Inhibitors in Drug Discovery: A Guide for Medicinal Chemists and Pharmacologists ( Second Edition). John Wiley & Sons, Inc. doi: 10.1002/9781118540398.
- Copeland, R. A., Basavapathruni, A., Moyer, M., & Scott, M. P. (2011). Impact of enzyme concentration and residence time on apparent activity recovery in jump dilution analysis. Analytical Biochemistry , 416(2), 206–210. doi: 10.1016/j.ab.2011.05.029.
- Copeland, R. A., Pompliano, D. L., & Meek, T. D. (2006). Drug–target residence time and its implications for lead optimization. Nature Reviews Drug Discovery , 5(9), 730–739. doi: 10.1038/nrd2082.
- Dalton, S. E., & Campos, S. (2020). Covalent small molecules as enabling platforms for drug discovery. ChemBioChem , 21(8), 1080–1100. doi: 10.1002/cbic.201900674.
- De Cesco, S., Kurian, J., Dufresne, C., Mittermaier, A. K., & Moitessier, N. (2017). Covalent inhibitors design and discovery. European Journal of Medicinal Chemistry , 138, 96–114. doi: 10.1016/j.ejmech.2017.06.019.
- Dharadhar, S., Kim, R. Q., Uckelmann, M., & Sixma, T. K. (2019). Chapter Thirteen - Quantitative analysis of USP activity in vitro. In M. Hochstrasser (Ed.), Methods in Enzymology (Vol. 618, 281–319). Academic Press. doi: 10.1016/bs.mie.2018.12.023.
- Engel, J., Richters, A., Getlik, M., Tomassi, S., Keul, M., Termathe, M., … Rauh, D. (2015). Targeting drug resistance in EGFR with covalent inhibitors: A structure-based design approach. Journal of Medicinal Chemistry , 58(17), 6844–6863. doi: 10.1021/acs.jmedchem.5b01082.
- Fell, J. B., Fischer, J. P., Baer, B. R., Blake, J. F., Bouhana, K., Briere, D. M., … Marx, M. A. (2020). Identification of the clinical development candidate MRTX849, a covalent KRASG12C inhibitor for the treatment of cancer. Journal of Medicinal Chemistry , 63(13), 6679–6693. doi: 10.1021/acs.jmedchem.9b02052.
- Ferrall-Fairbanks, M. C., Kieslich, C. A., & Platt, M. O. (2020). Reassessing enzyme kinetics: Considering protease-as-substrate interactions in proteolytic networks. Proceedings of the National Academy of Sciences , 117(6), 3307. doi: 10.1073/pnas.1912207117.
- Gabizon, R., & London, N. (2020). A fast and clean BTK inhibitor. Journal of Medicinal Chemistry , 63(10), 5100–5101. doi: 10.1021/acs.jmedchem.0c00597.
- Gehringer, M., & Laufer, S. A. (2019). Emerging and Re-Emerging Warheads for Targeted Covalent Inhibitors: Applications in Medicinal Chemistry and Chemical Biology. Journal of Medicinal Chemistry , 62(12), 5673–5724. doi: 10.1021/acs.jmedchem.8b01153.
- Guan, I., Williams, K., Pan, J., & Liu, X. (2021). New cysteine covalent modification strategies enable advancement of proteome-wide selectivity of kinase modulators. Asian Journal of Organic Chemistry , 10(5), 949–963. doi: 10.1002/ajoc.202100036.
- Hansen, R., Peters, U., Babbar, A., Chen, Y., Feng, J., Janes, M. R., … Zarrinkar, P. P. (2018). The reactivity-driven biochemical mechanism of covalent KRASG12C inhibitors. Nature Structural & Molecular Biology, 25(6), 454–462. doi: 10.1038/s41594-018-0061-5.
- Harris, C. M., Foley, S. E., Goedken, E. R., Michalak, M., Murdock, S., & Wilson, N. S. (2018). Merits and pitfalls in the characterization of covalent inhibitors of bruton's tyrosine Kinase. SLAS DISCOVERY: Advancing the Science of Drug Discovery , 23(10), 1040–1050. doi: 10.1177/2472555218787445.
- Holdgate, G. A., Meek, T. D., & Grimley, R. L. (2017). Mechanistic enzymology in drug discovery: A fresh perspective [Review Article]. Nature Reviews Drug Discovery , 17, 115. doi: 10.1038/nrd.2017.219.
- Ito, K., Iwatsubo, T., Kanamitsu, S., Ueda, K., Suzuki, H., & Sugiyama, Y. (1998). Prediction of pharmacokinetic alterations caused by drug-drug interactions: Metabolic interaction in the liver. Pharmacological Reviews , 50(3), 387. Retrieved from http://pharmrev.aspetjournals.org/content/50/3/387.abstract.
- Janssen, A. P. A., van Hengst, J. M. A., Béquignon, O. J. M., Deng, H., van Westen, G. J. P., & van der Stelt, M. (2019). Structure kinetics relationships and molecular dynamics show crucial role for heterocycle leaving group in irreversible diacylglycerol lipase inhibitors. Journal of Medicinal Chemistry , 62(17), 7910–7922. doi: 10.1021/acs.jmedchem.9b00686.
- Johansson, H., Isabella Tsai, Y.-C., Fantom, K., Chung, C.-W., Kümper, S., Martino, L., … Rittinger, K. (2019). Fragment-based covalent ligand screening enables rapid discovery of inhibitors for the RBR E3 ubiquitin ligase HOIP. Journal of the American Chemical Society , 141(6), 2703–2712. doi: 10.1021/jacs.8b13193.
- Johnson, D. S., Weerapana, E., & Cravatt, B. F. (2010). Strategies for discovering and derisking covalent, irreversible enzyme inhibitors. Future Medicinal Chemistry , 2(6), 949–964. doi: 10.4155/fmc.10.21.
- Johnson, I. D. (2010). Introduction to fluorescence techniques. In Molecular Probes Handbook: A Guide to Fluorescent Probes and Labeling Technologies ( 11th edition, pp. 2–9). Life Technologies Corporation. Available at https://www.thermofisher.com/nl/en/home/references/molecular-probes-the-handbook/introduction-to-fluorescence-techniques.html.
- Johnson, K. A. (2009). Fitting enzyme kinetic data with kintek global kinetic explorer. Methods in Enzymology , 467, 601–626. doi: 10.1016/S0076-6879(09)67023-3.
- Kathman, S. G., Xu, Z., & Statsyuk, A. V. (2014). A fragment-based method to discover irreversible covalent inhibitors of cysteine proteases. Journal of Medicinal Chemistry , 57(11), 4969–4974. doi: 10.1021/jm500345q.
- Kathman, S. G., & Statsyuk, A. V. (2019). Methodology for identification of cysteine-reactive covalent inhibitors. In P. Hogg (Ed.), Functional Disulphide Bonds: Methods and Protocols (pp. 245–262). New York: Springer. doi: 10.1007/978-1-4939-9187-7_15.
- Kim, H., Hwang, Y. S., Kim, M., & Park, S. B. (2021). Recent advances in the development of covalent inhibitors. RSC Medicinal Chemistry , 12(7), 1037–1045. doi: 10.1039/D1MD00068C.
- Kitz, R., & Wilson, I. B. (1962). Esters of methanesulfonic acid as irreversible inhibitors of acetylcholinesterase. Journal of Biological Chemistry , 237(10), 3245–3249. doi: 10.1016/S0021-9258(18)50153-8.
- Krippendorff, B.-F., Neuhaus, R., Lienau, P., Reichel, A., & Huisinga, W. (2009). Mechanism-based inhibition: Deriving KI and k inact directly from time-dependent IC50 values. Journal of Biomolecular Screening , 14(8), 913–923. doi: 10.1177/1087057109336751.
- Kuzmič, P. (2009). Chapter 10 - DynaFit—a software package for enzymology. In M. L. Johnson & L. Brand (Eds.), Methods in Enzymology (Vol. 467, 247–280). Academic Press. doi: 10.1016/S0076-6879(09)67010-5.
- Kuzmič, P. (2015). Determination of kinact and Ki for covalent inhibition using the Omnia® assay [BioKin Technical Note TN-2015-02]. Watertown MA: BioKin Ltd., [Online]. Available at www.biokin.com/TN/2015/02.
- Kuzmič, P. (2020a). A steady-state algebraic model for the time course of covalent enzyme inhibition. bioRxiv. doi: 10.1101/2020.06.10.144220.
- Kuzmič, P. (2020b). A two-point IC50 method for evaluating the biochemical potency of irreversible enzyme inhibitors. bioRxiv. doi: 10.1101/2020.06.25.171207.
- Kuzmič, P., Solowiej, J., & Murray, B. W. (2015). An algebraic model for the kinetics of covalent enzyme inhibition at low substrate concentrations. Analytical Biochemistry , 484, 82–90. doi: 10.1016/j.ab.2014.11.014.
- Lagoutte, R., Patouret, R., & Winssinger, N. (2017). Covalent inhibitors: An opportunity for rational target selectivity. Current Opinion in Chemical Biology , 39, 54–63. doi: 10.1016/j.cbpa.2017.05.008.
- Lanman, B. A., Allen, J. R., Allen, J. G., Amegadzie, A. K., Ashton, K. S., Booker, S. K., … Cee, V. J. (2020). Discovery of a covalent inhibitor of KRASG12C (AMG 510) for the treatment of solid tumors. Journal of Medicinal Chemistry , 63(1), 52–65. doi: 10.1021/acs.jmedchem.9b01180.
- Lee, C.-U., & Grossmann, T. N. (2012). Reversible covalent inhibition of a protein target. Angewandte Chemie International Edition , 51(35), 8699–8700. doi: 10.1002/anie.201203341.
- Liclican, A., Serafini, L., Xing, W., Czerwieniec, G., Steiner, B., Wang, T., … Feng, J. Y. (2020). Biochemical characterization of tirabrutinib and other irreversible inhibitors of Bruton's tyrosine kinase reveals differences in on - and off - target inhibition. Biochimica et Biophysica Acta (BBA) - General Subjects , 1864(4), 129531. doi: 10.1016/j.bbagen.2020.129531.
- Lonsdale, R., Burgess, J., Colclough, N., Davies, N. L., Lenz, E. M., Orton, A. L., & Ward, R. A. (2017). Expanding the armory: Predicting and tuning covalent warhead reactivity. Journal of Chemical Information and Modeling , 57(12), 3124–3137. doi: 10.1021/acs.jcim.7b00553.
- Lu, S., & Zhang, J. (2017). Designed covalent allosteric modulators: An emerging paradigm in drug discovery. Drug Discovery Today , 22(2), 447–453. doi: 10.1016/j.drudis.2016.11.013.
- Mah, R., Thomas, J. R., & Shafer, C. M. (2014). Drug discovery considerations in the development of covalent inhibitors. Bioorganic & Medicinal Chemistry Letters, 24(1), 33–39. doi: 10.1016/j.bmcl.2013.10.003.
- Martin, J. S., MacKenzie, C. J., Fletcher, D., & Gilbert, I. H. (2019). Characterising covalent warhead reactivity. Bioorganic & Medicinal Chemistry, 27(10), 2066–2074. doi: 10.1016/j.bmc.2019.04.002.
- Mayer, J., Khairy, K., & Howard, J. (2010). Drawing an elephant with four complex parameters. American Journal of Physics , 78(6), 648–649. doi: 10.1119/1.3254017.
- McWhirter, C. (2021). Chapter One - Kinetic mechanisms of covalent inhibition. In R. A. Ward & N. P. Grimster (Eds.), Annual Reports in Medicinal Chemistry (Vol. 56, pp. 1–31). Academic Press. doi: 10.1016/bs.armc.2020.11.001.
- Meara, J. P., & Rich, D. H. (1995). Measurement of individual rate constants of irreversible inhibition of a cysteine proteinase by an epoxysuccinyl inhibitor. Bioorganic & Medicinal Chemistry Letters, 5(19), 2277–2282. doi: 10.1016/0960-894X(95)00396-B.
- Miyawaki, O., Kanazawa, T., Maruyama, C., & Dozen, M. (2017). Static and dynamic half-life and lifetime molecular turnover of enzymes. Journal of Bioscience and Bioengineering , 123(1), 28–32. doi: 10.1016/j.jbiosc.2016.07.016.
- Mons, E., Jansen, I. D. C., Loboda, J., van Doodewaerd, B. R., Hermans, J., Verdoes, M., … Ovaa, H. (2019). The alkyne moiety as a latent electrophile in irreversible covalent small molecule inhibitors of cathepsin K. Journal of the American Chemical Society , 141(8), 3507–3514. doi: 10.1021/jacs.8b11027.
- Mons, E., Kim, R. Q., van Doodewaerd, B. R., van Veelen, P. A., Mulder, M. P. C., & Ovaa, H. (2021). Exploring the versatility of the covalent thiol–alkyne reaction with substituted propargyl warheads: A deciding role for the cysteine protease. Journal of the American Chemical Society , 143(17), 6423–6433. doi: 10.1021/jacs.0c10513.
- Motulsky, H. J. (1995-2021). Graphpad Curve Fitting Guide. GraphPad Software, LLC. https://www.graphpad.com/guides/prism/latest/curve-fitting/reg_writing_models.htm.
- Motulsky, H. J., & Christopoulos, A. (2003). Fitting Models to Biological Data Using Linear and Nonlinear Regression: A Practical Guide to Curve Fitting. ISBN-13: 978-0195171808; ISBN-10: 1425919448. GraphPad Software Inc. Available at https://www.amazon.com/Fitting-Models-Biological-Nonlinear-Regression/dp/0195171802.
- Murphy, D. J. (2004). Determination of accurate KI values for tight-binding enzyme inhibitors: An in silico study of experimental error and assay design. Analytical Biochemistry , 327(1), 61–67. doi: 10.1016/j.ab.2003.12.018.
- Obach, R. S., Walsky, R. L., & Venkatakrishnan, K. (2007). Mechanism-based inactivation of human cytochrome p450 enzymes and the prediction of drug-drug interactions. Drug Metabolism and Disposition , 35(2), 246. doi: 10.1124/dmd.106.012633.
- Owen Dafydd, R., Allerton Charlotte, M. N., Anderson Annaliesa, S., Aschenbrenner, L., Avery, M., Berritt, S., … Zhu, Y. (2021). An oral SARS-CoV-2 Mpro inhibitor clinical candidate for the treatment of COVID-19. Science , eabl4784. doi: 10.1126/science.abl4784.
- Perrin, C. L. (2017). Linear or nonlinear least-squares analysis of kinetic data? Journal of Chemical Education , 94(6), 669–672. doi: 10.1021/acs.jchemed.6b00629.
- Pollard, T. D., & De La Cruz, E. M. (2013). Take advantage of time in your experiments: A guide to simple, informative kinetics assays. Molecular Biology of the Cell , 24(8), 1103–1110. doi: 10.1091/mbc.e13-01-0030.
- Potratz, J. P. (2018). Making enzyme kinetics dynamic via simulation software. Journal of Chemical Education , 95(3), 482–486. doi: 10.1021/acs.jchemed.7b00350.
- Ray, S., & Murkin, A. S. (2019). New electrophiles and strategies for mechanism-based and targeted covalent inhibitor design. Biochemistry , 58(52), 5234–5244. doi: 10.1021/acs.biochem.9b00293.
- Resnick, E., Bradley, A., Gan, J., Douangamath, A., Krojer, T., Sethi, R., … London, N. (2019). Rapid covalent-probe discovery by electrophile-fragment screening. Journal of the American Chemical Society , 141(22), 8951–8968. doi: 10.1021/jacs.9b02822.
- Rocha-Pereira, J., Nascimento, M. S. J., Ma, Q., Hilgenfeld, R., Neyts, J., & Jochmans, D. (2014). The enterovirus protease inhibitor rupintrivir exerts cross-genotypic anti-norovirus activity and clears cells from the norovirus replicon. Antimicrobial Agents and Chemotherapy , 58(8), 4675–4681. doi: 10.1128/AAC.02546-13.
- Rufer, A. C. (2021). Drug discovery for enzymes. Drug Discovery Today , 26(4), 875–886. doi: 10.1016/j.drudis.2021.01.006.
- Schwartz, P. A., Kuzmic, P., Solowiej, J., Bergqvist, S., Bolanos, B., Almaden, C., … Murray, B. W. (2014). Covalent EGFR inhibitor analysis reveals importance of reversible interactions to potency and mechanisms of drug resistance. Proceedings of the National Academy of Sciences , 111(1), 173. doi: 10.1073/pnas.1313733111.
- Selwyn, M. J. (1965). A simple test for inactivation of an enzyme during assay. Biochimica et Biophysica Acta (BBA) - Enzymology and Biological Oxidation , 105(1), 193–195. doi: 10.1016/S0926-6593(65)80190-4.
- Serafimova, I. M., Pufall, M. A., Krishnan, S., Duda, K., Cohen, M. S., Maglathlin, R. L., … Taunton, J. (2012). Reversible targeting of noncatalytic cysteines with chemically tuned electrophiles. Nature Chemical Biology , 8(5), 471–476. doi: 10.1038/nchembio.925.
- Shindo, N., & Ojida, A. (2021). Recent progress in covalent warheads for in vivo targeting of endogenous proteins. Bioorganic & Medicinal Chemistry, 47, 116386. doi: 10.1016/j.bmc.2021.116386.
- Singh, J., Petter, R. C., Baillie, T. A., & Whitty, A. (2011). The resurgence of covalent drugs. Nature Reviews Drug Discovery , 10(4), 307–317. doi: 10.1038/nrd3410.
- Smith, S., Keul, M., Engel, J., Basu, D., Eppmann, S., & Rauh, D. (2017). Characterization of covalent-reversible EGFR inhibitors. ACS Omega , 2(4), 1563–1575. doi: 10.1021/acsomega.7b00157.
- Strelow, J. M. (2017). A perspective on the kinetics of covalent and irreversible inhibition. SLAS DISCOVERY: Advancing Life Sciences R &D, 22(1), 3–20. doi: 10.1177/1087057116671509.
- Stresser, D. M., Mao, J., Kenny, J. R., Jones, B. C., & Grime, K. (2014). Exploring concepts of in vitro time-dependent CYP inhibition assays. Expert Opinion on Drug Metabolism & Toxicology, 10(2), 157–174. doi: 10.1517/17425255.2014.856882.
- Telliez, J.-B., Dowty, M. E., Wang, L., Jussif, J., Lin, T., Li, L., … Thorarensen, A. (2016). Discovery of a JAK3-selective inhibitor: Functional differentiation of JAK3-selective inhibition over pan-JAK or JAK1-selective inhibition. ACS Chemical Biology , 11(12), 3442–3451. doi: 10.1021/acschembio.6b00677.
- Tuley, A., & Fast, W. (2018). The taxonomy of covalent inhibitors. Biochemistry , 57(24), 3326–3337. doi: 10.1021/acs.biochem.8b00315.
- Walkup, G. K., You, Z., Ross, P. L., Allen, E. K. H., Daryaee, F., Hale, M. R., … Fisher, S. L. (2015). Translating slow-binding inhibition kinetics into cellular and in vivo effects. Nature Chemical Biology , 11(6), 416–423. doi: 10.1038/nchembio.1796.
- Ward, R. A., & Grimster, N. P. (2021). The design of covalent-based inhibitors. Annual Reports in Medicinal Chemistry , 56, 2–284. Available at https://www.sciencedirect.com/bookseries/annual-reports-in-medicinal-chemistry/vol/56/suppl/C.
- Wu, G., Yuan, Y., & Hodge, C. N. (2003). Determining appropriate substrate conversion for enzymatic assays in high-throughput screening. Journal of Biomolecular Screening , 8(6), 694–700. doi: 10.1177/1087057103260050.
- Yang, J., Jamei, M., Yeo, K. R., Tucker, G. T., & Rostami-Hodjegan, A. (2005). Kinetic values for mechanism-based enzyme inhibition: Assessing the bias introduced by the conventional experimental protocol. European Journal of Pharmaceutical Sciences , 26(3), 334–340. doi: 10.1016/j.ejps.2005.07.005.
- Zhai, X., Ward, R. A., Doig, P., & Argyrou, A. (2020). Insight into the therapeutic selectivity of the irreversible EGFR tyrosine kinase inhibitor osimertinib through enzyme kinetic studies. Biochemistry , 59(14), 1428–1441. doi: 10.1021/acs.biochem.0c00104.
- Zhang, J.-H., Chung, T. D. Y., & Oldenburg, K. R. (1999). A simple statistical parameter for use in evaluation and validation of high throughput screening assays. Journal of Biomolecular Screening , 4(2), 67–73. doi: 10.1177/108705719900400206.
- Zhang, T., Hatcher, J. M., Teng, M., Gray, N. S., & Kostic, M. (2019). Recent advances in selective and irreversible covalent ligand development and validation. Cell Chemical Biology , 26(11), 1486–1500. doi: 10.1016/j.chembiol.2019.09.012.
Internet Resources
Interactive kinetic simulation scripts used to generate figures in this work, including a tutorial on how to use them. Note: loading this page for the first time can take up to 5 min, and involves an automatic redirection (reloading) to the Landing Page. Full URL: https://mybinder.org/v2/gh/sroet/Elma/main?labpath=Landing%20Page.ipynb
Online assay guidance manual for general assay optimization managed by the National Center for Advancing Translational Sciences (NCATS)
Online guide on implementing user-defined equations for nonlinear regression in GraphPad Prism
Citing Literature
Number of times cited according to CrossRef: 12
- Elma Mons, Robbert Q. Kim, Monique P. C. Mulder, Technologies for Direct Detection of Covalent Protein–Drug Adducts, Pharmaceuticals, 10.3390/ph16040547, 16 , 4, (547), (2023).
- Jay Yang, Yudai Tabuchi, Riku Katsuki, Masumi Taki, bioTCIs: Middle-to-Macro Biomolecular Targeted Covalent Inhibitors Possessing Both Semi-Permanent Drug Action and Stringent Target Specificity as Potential Antibody Replacements, International Journal of Molecular Sciences, 10.3390/ijms24043525, 24 , 4, (3525), (2023).
- Ricardo A.M. Serafim, Lisa Haarer, Júlia G.B. Pedreira, Matthias Gehringer, Covalent chemical probes for protein kinases, Current Research in Chemical Biology, 10.1016/j.crchbi.2022.100040, 3 , (100040), (2023).
- Yongfeng Tao, Jan G. Felber, Zhongyu Zou, Evert Njomen, Jarrett R. Remsberg, Daisuke Ogasawara, Chang Ye, Bruno Melillo, Stuart L. Schreiber, Chuan He, David Remillard, Benjamin F. Cravatt, Chemical Proteomic Discovery of Isotype‐Selective Covalent Inhibitors of the RNA Methyltransferase NSUN2, Angewandte Chemie International Edition, 10.1002/anie.202311924, 62 , 51, (2023).
- Alejandro Mahía, Anders E. Kiib, Marija Nisavic, Esben B. Svenningsen, Johan Palmfeldt, Thomas B. Poulsen, α‐Lactam Electrophiles for Covalent Chemical Biology** , Angewandte Chemie International Edition, 10.1002/anie.202304142, 62 , 26, (2023).
- Yongfeng Tao, Jan G. Felber, Zhongyu Zou, Evert Njomen, Jarrett R. Remsberg, Daisuke Ogasawara, Chang Ye, Bruno Melillo, Stuart L. Schreiber, Chuan He, David Remillard, Benjamin F. Cravatt, Chemical Proteomic Discovery of Isotype‐Selective Covalent Inhibitors of the RNA Methyltransferase NSUN2, Angewandte Chemie, 10.1002/ange.202311924, 135 , 51, (2023).
- Alejandro Mahía, Anders E. Kiib, Marija Nisavic, Esben B. Svenningsen, Johan Palmfeldt, Thomas B. Poulsen, α‐Lactam Electrophiles for Covalent Chemical Biology** , Angewandte Chemie, 10.1002/ange.202304142, 135 , 26, (2023).
- David E. Heppner, Florian Wittlinger, Tyler S. Beyett, Tatiana Shaurova, Daniel A. Urul, Brian Buckley, Calvin D. Pham, Ilse K. Schaeffner, Bo Yang, Blessing C. Ogboo, Earl W. May, Erik M. Schaefer, Michael J. Eck, Stefan A. Laufer, Pamela A. Hershberger, Structural Basis for Inhibition of Mutant EGFR with Lazertinib (YH25448), ACS Medicinal Chemistry Letters, 10.1021/acsmedchemlett.2c00213, 13 , 12, (1856-1863), (2022).
- Yuqing Jia, Robbert Q. Kim, Raymond Kooij, Huib Ovaa, Aysegul Sapmaz, Paul P. Geurink, Chemical Toolkit for PARK7: Potent, Selective, and High-Throughput, Journal of Medicinal Chemistry, 10.1021/acs.jmedchem.2c01113, 65 , 19, (13288-13304), (2022).
- Marija S. Genčić, Nikola M. Stojanović, Marko Z. Mladenović, Niko S. Radulović, An HPLC-based assay for improved measurement of glutamate decarboxylase inhibition/activation, Neurochemistry International, 10.1016/j.neuint.2022.105433, 161 , (105433), (2022).
- Marco Daniele Parenti, Marina Naldi, Elisabetta Manoni, Edoardo Fabini, Daniela Cederfelt, Vladimir O. Talibov, Valeria Gressani, Ummu Guven, Valentina Grossi, Candida Fasano, Paola Sanese, Katia De Marco, Alexander A. Shtil, Alexander V. Kurkin, Andrea Altieri, U. Helena Danielson, Giuseppina Caretti, Cristiano Simone, Greta Varchi, Manuela Bartolini, Alberto Del Rio, Discovery of the 4-aminopiperidine-based compound EM127 for the site-specific covalent inhibition of SMYD3, European Journal of Medicinal Chemistry, 10.1016/j.ejmech.2022.114683, 243 , (114683), (2022).
- Ling Wang, Shibo Sun, Haowen Liu, Qiuyu Zhang, Yao Meng, Fan Sun, Jianjun Zhang, Haiyan Liu, Weiping Xu, Zhiwei Ye, Jie Zhang, Bingbing Sun, Jianqiang Xu, Thioredoxin reductase inhibition and glutathione depletion mediated by glaucocalyxin A promote intracellular disulfide stress in gastric cancer cells, The FEBS Journal, 10.1111/febs.17301.