Causal diagrams such as directed acyclic graphs (DAGs) are used in several scientific fields to help design and analyze studies that aim to infer causal effects from observational data; for example, DAGs can help identify suitable strategies to reduce confounding bias. However, DAGs can be difficult to design, and the validity of any DAG-derived strategy hinges on the validity of the postulated DAG itself. Researchers should therefore check whether the assumptions encoded in the DAG are consistent with the data before proceeding with the analysis. Here, we explain how the R package ‘dagitty’, based on the web tool dagitty.net, can be used to test the statistical implications of the assumptions encoded in a given DAG. We hope that this will help researchers discover model specification errors, avoid erroneous conclusions, and build better models. © 2021 The Authors.

This article was corrected on 19 July 2022. See the end of the full text for details.

Basic Protocol 1 : Constructing and importing DAG models from the dagitty web interface

Support Protocol 1 : Installing R, RStudio, and the dagitty package

Basic Protocol 2 : Testing DAGs against categorical data

Basic Protocol 3 : Testing DAGs against continuous data

Support Protocol 2 : Testing DAGs against continuous data with non-linearities

Basic Protocol 4 : Testing DAGs against a combination of categorical and continuous data

In causal inference, directed acyclic graphs (DAGs) are intuitive diagrams of cause-effect relationships. Such diagrams provide a firm methodological basis for answering causal queries from observational data. The web-based tool dagitty.net (Textor, Hardt, & Knüppel, 2011) allows users to build and analyze the structure of DAGs and is currently accessed by several hundred unique visitors per day.

However, the emphasis of dagitty.net lies on the graphical structure of DAGs. Yet a major strength of DAGs is that these structures can be tested against datasets containing some or all of the variables from which the DAG is built. The R package ‘dagitty’, therefore, complements dagitty.net with methods to facilitate such testing (Textor, Zander, Gilthorpe, Liśkiewicz, & Ellison, 2016). The protocols presented here are aimed at users who are already familiar with DAGs and wish to test the implications of a given DAG model statistically. We assume that users are reasonably familiar with the R platform for statistical computing, although we do not require much knowledge in R and have prepared Support Protocol 1 which explains how to install R, RStudio, and the R package ‘dagitty’ for first-time users.

The testable implications of DAGs take the form of conditional independence statements (Thoemmes, Rosseel, & Textor, 2018). Statistical testing of such independencies always involves showing that the variables in question are uncorrelated (possibly after conditioning on some other variables), but the exact tests used depend on the nature of the data at hand: testing whether the (continuous) expression levels of two genes are (un)correlated involves a different test than checking whether having a certain cancer (a binary yes/no variable) is associated with gender (another categorical variable). The protocols in this article are organized accordingly. Basic Protocol 1 starts off by explaining how to construct a DAG on dagitty.net and import it into R for further processing. Support Protocol 1 gives details for installing the tools required for the protocols. Basic Protocol 2 then explains how to test a DAG with a dataset that contains mostly discrete variables. By contrast, Basic Protocol 3 focuses on continuous, linearly dependent variables; Support Protocol 2 extends these methods to scenarios where the linearity assumption does not hold. Finally, Basic Protocol 4 deals with datasets where some variables are categorical and others are continuous. For a more detailed explanation of the role of DAGs in causal inference and the importance of model testing, we refer the reader to the Commentary at the end of this article.

Testing a DAG in dagitty requires two inputs: (1) the hypothesized, graphical DAG model to test, and (2) the corresponding data. This protocol describes how to obtain the former. Although it is possible to enter a DAG in the R package directly, the easiest way to construct a DAG is to use the web interface at dagitty.net—where the model can be exported for easy loading into R.

Necessary Resources

Hardware

Any computer that can run R and a web browser

Software

• Web browser: any major standards-compliant browser
• Operating system: any operating system that can run R and a web browser
• R: version 3.6 or higher
• R package ‘dagitty’ version 0.3.0 or higher

Files

None

1.Go to dagitty.net. You will see a caption Launch , where you can click on Launch dagitty online in your browser. This will open up the GUI with an example DAG already drawn (Fig. 1). The GUI has a left, upper, and right menu, as well as the canvas where the DAG is drawn—see Figure 1.Note that the upper menu has a “How to” that can be used in addition to this tutorial.

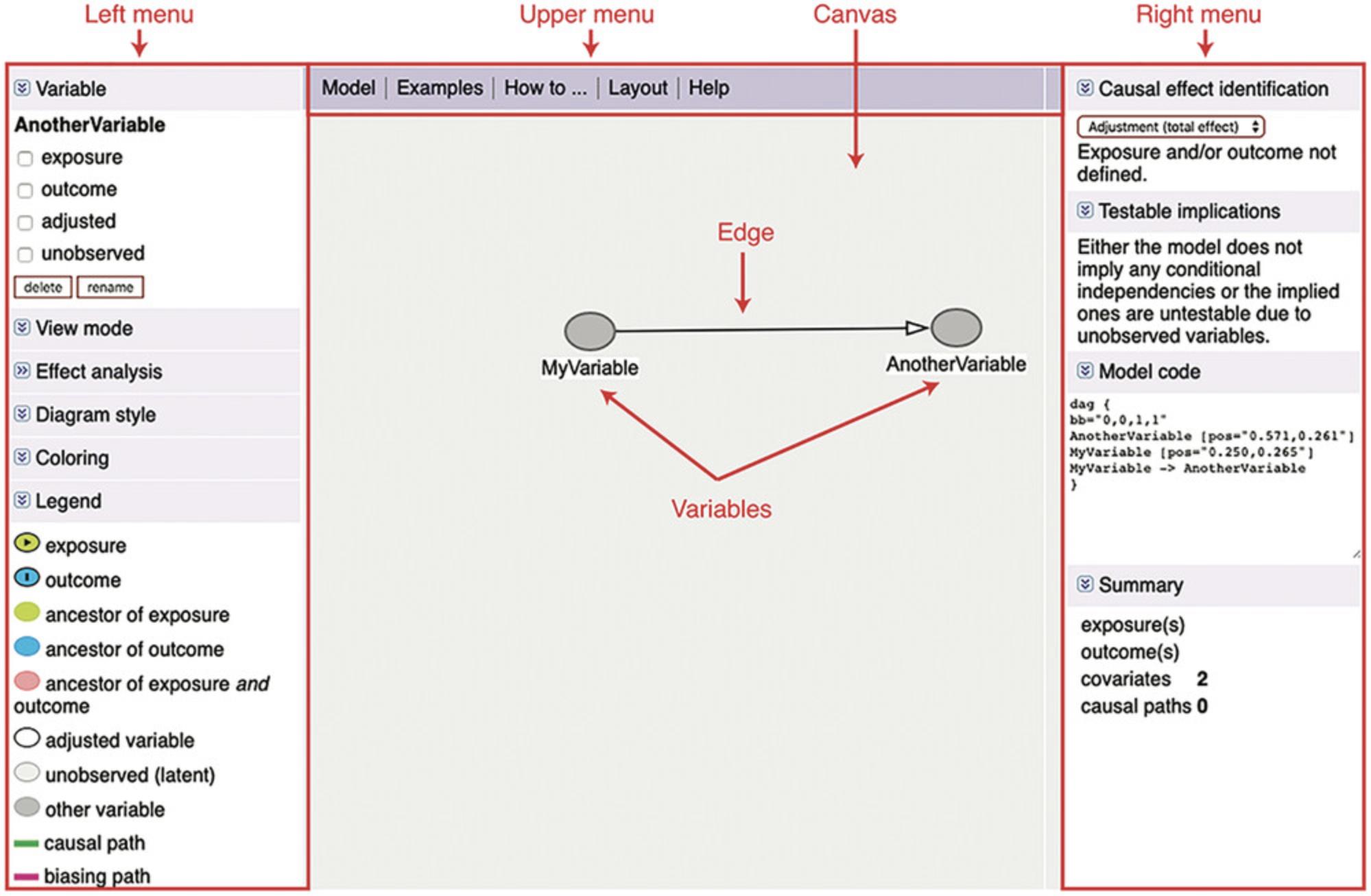
2.In the upper menu, click Model > New model. This will clear the canvas to draw a new DAG from scratch. Instead of drawing a DAG from scratch, users can also load and continue with a previous DAG by copying and pasting code in the Model code tab in the right menu. See step 8 for details.

3.Click anywhere on the empty canvas to add a new variable to the DAG. Give it a name and click “OK.” Repeat to include all variables of the DAG.

4.Optional : Rearrange variables on the canvas if necessary. To select a variable, click it. You can delete or rename it in the Variable panel on the upper left of the page. To move it, just drag it to its new place.

5.Add edges. For example, to add a directed edge from a variable A to a variable B , first click once on A and then once on B. Users can remove an existing edge by clicking once more first on A , then on B. To make a bidirected edge, first add the edge A → B as described, and then add the reverse edge B → A by clicking B , then A. Note that a bidirected edge A ↔ B in a DAG is shorthand for a structure A ← U → B , where A and B are correlated because they have some (unobserved) common cause U.

6.Optional : Clean up the DAG layout. For DAGs with many variables and edges, it can be difficult to find a clear and “readable” layout that properly shows the model. In the upper menu, try clicking Layout > Generate layout automatically to auto-generate a layout. Users can try this step multiple times until they find a satisfactory option.

7.Optional : Save an image of your DAG. Click the Model tab in the upper menu, and select your export option of choice. Users can save their DAG in PDF, PNG, JPEG, or SVG format. Alternatively, LateX users can export LateX code for drawing the DAG using the tikz package (Tantau, 2007).

8.Optional : Save the DAG for later use. Copy-paste the text in the Model code tab in the right menu into any text editor, and save it for later use. This code can be used for importing the DAG into R or in the dagitty web interface, see step 2.

9.Open R and load the dagitty package:

• library( dagitty )

First-time users first need to install the dagitty package—please refer to Support Protocol 1.

10.Import your DAG into R and save it into a variable myDAG using the following command:

• myDAG <- dagitty( "[code here]" )

In the place of [code here], copy-paste the code from the Model code tab in the right menu of the dagitty web GUI. The entire code becomes something like this:

• myDAG <- dagitty( 'dag {
  • bb="0,0,1,1"
  • AnotherVariable [pos="0.571,0.261"]
  • MyVariable [pos="0.250,0.265"]
  • MyVariable -> AnotherVariable
  • }' )

Do not forget the quotation marks around the code as copy-pasted from the web GUI. Your DAG is now ready for use in the R package; see the other basic protocols in this article.

11.Optional : Plot the DAG to verify that it has been successfully imported:

• plot( myDAG )

For users unfamiliar with R, this protocol describes how to get started with R and install the dagitty and lavaan packages.

Necessary Resources

Hardware

Any computer that can run R and a web browser

Software

• Web browser: any major standards-compliant browser
• Operating system: any operating system that can run R and a web browser
• R: version 3.6 or higher
• R package ‘dagitty’ version 0.3.0 or higher

Files

None

1.Download and install R on your computer. Visit https://cloud.r-project.org/ and follow the instructions.

2.Download and install RStudio from https://rstudio.com/products/rstudio/download/. Open RStudio; you will see a GUI as in Figure 2.

The RStudio window has several areas, including the console and plotting area (Fig. 2). When the bottom line in the console reads >, this means R is ready for users to type their commands.

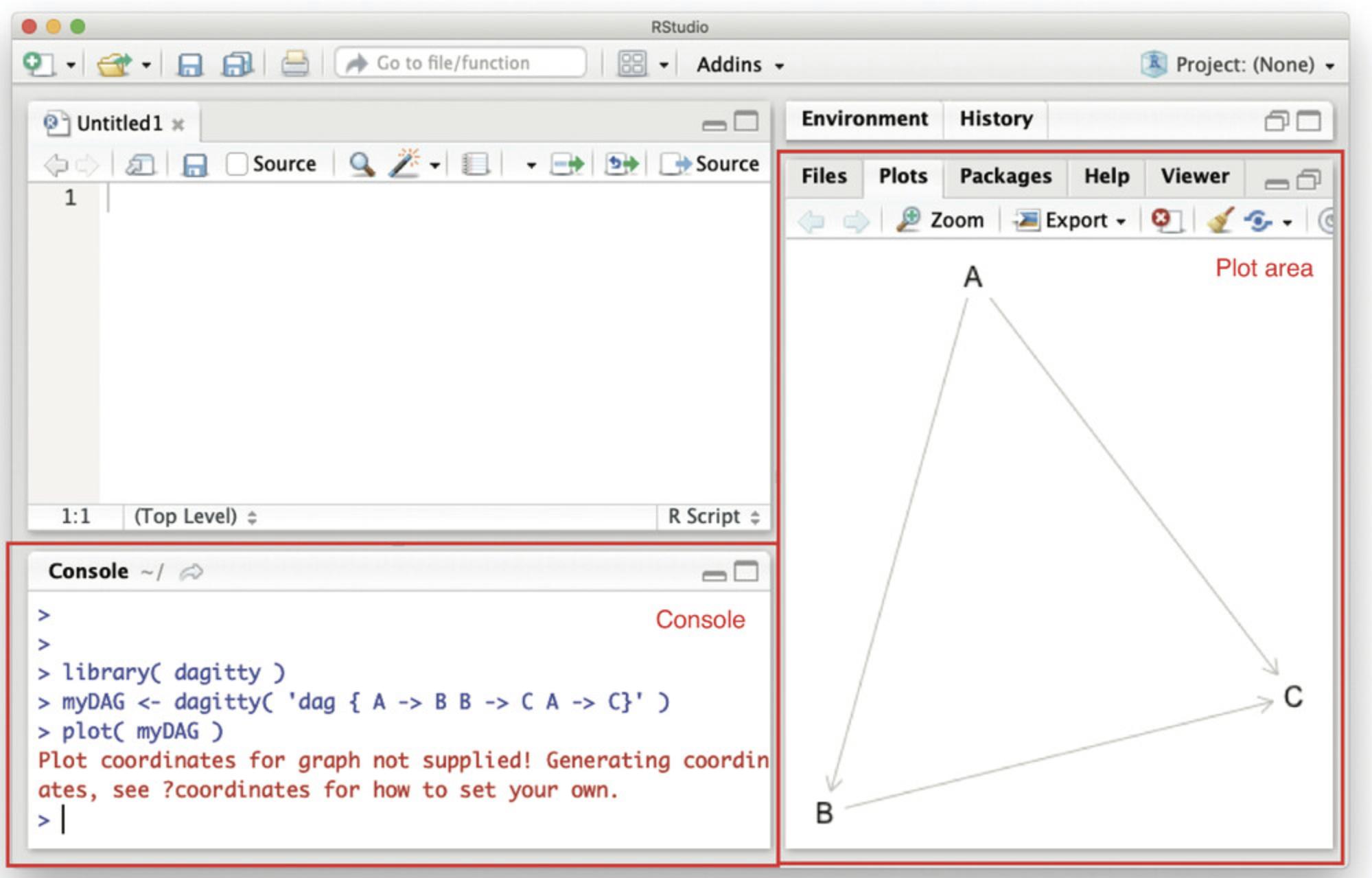
3.Install the dagitty package. In the console (Fig. 2), type:

• install.packages( "dagitty" )

and hit Enter. This will install the dagitty package in R.

Note that a working internet connection is required to download and install R packages. The install.packages() command may ask users to choose a “CRAN mirror” from where to download the package. If this occurs, type 1 and hit enter. This will install the package from the cloud, which is always a safe option. You will see text appearing in the console while the package is installing—this is normal. Wait until you see > again, which means the installation is finished.

4.Load the dagitty package by typing into the console (Fig. 2):

• library( dagitty )

dagitty should now be ready for use. By default, R does not load all functions it comes with because this would be inefficient. Users therefore have to load a package first if they wish to use it.

5.If all went well, you should now be able to plot a first DAG. Try:

• myDAG <- dagitty( "dag {A -> B -> C A -> C}" )
• plot( myDAG )

A DAG with three variables (A , B , and C) should now appear in the plot area (Fig. 2). Beware of typos when entering commands in R. Like any programming language, R is not very smart and does not understand you when you type something slightly different from what you intended. For example, if you have called your dag myDAG, R will not understand you if you try to plot(MyDAG): it is case sensitive.

6.You can open a help page by typing ? immediately followed by the function name. For example, try ?dagitty to find out what the dagitty() function does.

7.Install the lavaan package. Similar to step 3, in the console (Fig. 2), type:

• install.packages( "lavaan" )

and hit Enter. The installation can be verified by loading the package using:

• library( lavaan )

After successful installation, this command should not give any error messages.

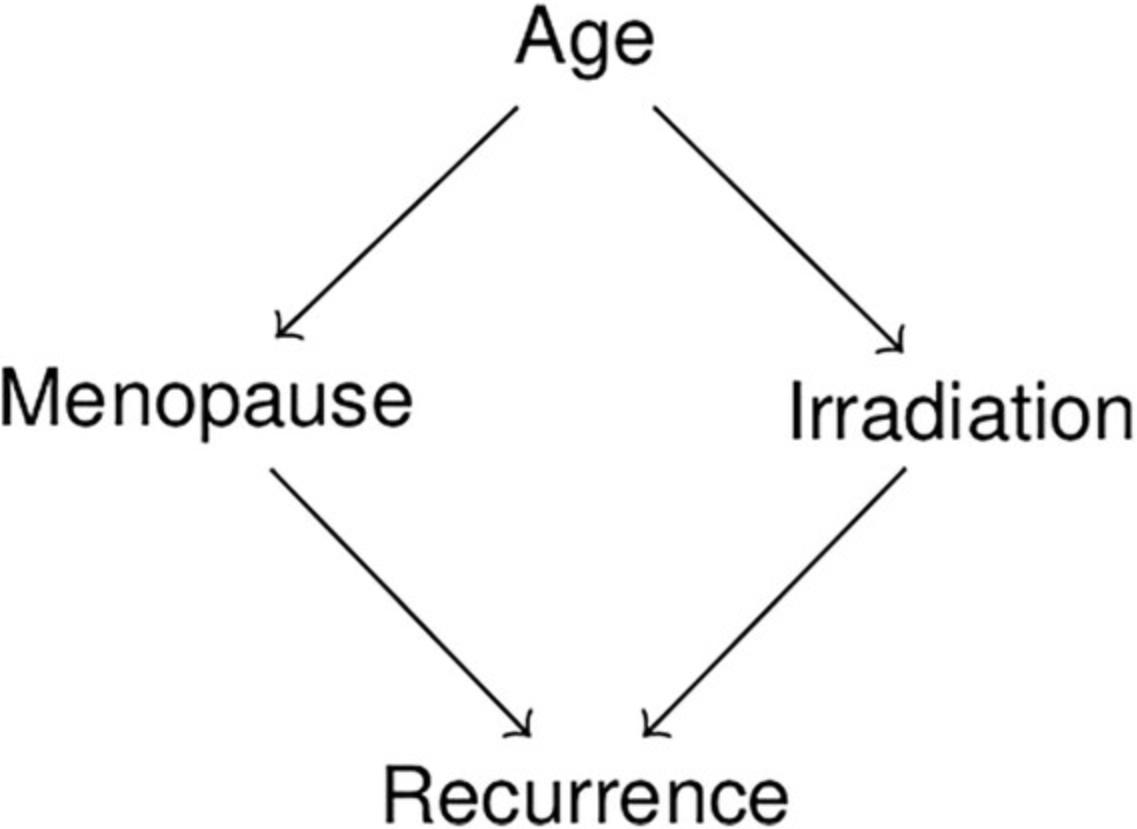
This protocol describes how to test the implied conditional independencies of a DAG against a dataset with only categorical variables. We use the DAG shown in Figure 3 along with simulated data to show an example of testing. We also provide a supplementary tutorial in Supporting Information, which contains a specific, worked-out example to illustrate how statistical testing and domain knowledge can be combined to test a DAG.

Necessary Resources

Hardware

Any computer that can run R and a web browser

Software

• Web browser: any major standards-compliant browser
• Operating system: any operating system that can run R and a web browser
• R: version 3.6 or higher
• R package ‘dagitty’ version 0.3.0 or higher

Files

brca.txt (download at: https://github.com/ankurankan/2020-dagitty-manual/)

1.Open R and load the dagitty package using:

• library( dagitty )

2.Import the DAG to be tested into R as described in Basic Protocol 1 (Fig. 3).

• myDAG <- dagitty( 'dag {
  • Age -> Irradiation
  • Age -> Menopause
  • Irradiation -> Recurrence
  • Menopause -> Recurrence
  • }' )

We recommend plotting the DAG at this point, to check that it has been correctly imported:

• plot( myDAG )

3.Import the data. In this case, since our data is a text file, we can use the read.table function:

• data <- read.table( "brca.txt", header=TRUE )

The exact commands required to import data in R depend on how the data are stored. Since dagitty is an R package, we assume here that readers are familiar with the methods for importing data into R. If not, readers can refer to ?read.table to see the options for reading in data—or to the free book Grolemund & Wickham (2020), which is an excellent resource for learning how to handle data in R. We also provide a simulated example dataset as a text file with a format that can be imported using the line of code mentioned above, so readers unfamiliar with R can use this example to get their data in the correct format before loading into R.

4.Test if implied independencies are contradicted by the data (Fig. 4). To do this, we will first generate a list of the independencies that are implied by the DAG.

• impliedConditionalIndependencies( myDAG )

This will show that there are two conditional independencies that are implied: “Age ⊥ Recurrence | Irradiation, Menopause” and “Irradiation ⊥ Menopause | Age.” To test these, we use the command ciTest as follows:

• ciTest( "Age", "Recurrence", c( "Irradiation", "Menopause" ),
  • data, type= "cis.chisq" )
• ciTest( "Irradiation", "Menopause", "Age", data, type="cis.chisq" )

Since the variables are categorical, a chi-square test is used to test for correlations between them. If one of the independencies is contradicted, this is reflected by a low p -value and high RMSEA and χ². See Guidelines for Understanding Results for more information.

There is an alternative method available that automatically lists relevant independencies implied by the input DAG, tests them, and returns all results in a single table (shown in Fig. 4):

• localTests( myDAG, data, type="cis.chisq" )

In this case, the results do not support the first independence, “Age ⊥ Recurrence | Irradiation, Menopause.” This could mean, for example, that a direct effect exists from Age to Recurrence that is not mediated by either Irradiation or Menopause. It could also mean that one or both of the variables “Irradiation” or “Menopause” have not been measured sufficiently precisely to capture the corresponding indirect effects in full, which can create the illusion of a residual direct effect. See Guidelines for Understanding Results for more information.

5.Optional : Correct the DAG if necessary. If the model is falsified by significant associations between variables that should be independent of each other, users may opt to adapt their DAG model by adding an extra arrow, such that the problematic independency is no longer implied by the model. For an example, see the tutorial in Supporting Information. However, changing models is a process that should be handled with care and always supported by domain knowledge. Significant p -values are not necessarily proof that the model is incorrect; they can also indicate problems with the data (pre)processing or the dataset itself. See Guidelines for Understanding Results for more information.

In the case of continuous datasets, dagitty tests for conditional independence using linear regression. Given a conditional independence condition X ⊥ Y |Z , first the residuals for the regressions X ∼ Z and Y ∼ Z are computed for each data point. Then, a statistical test determines whether a significant correlation exists between the residuals. If the independence condition holds, the residuals from these regressions should be statistically independent, and therefore uncorrelated.

Since this test relies on linear regression, it makes the following assumptions about the dataset: (1) linearity (relationships between variables are linear); (2) multivariate normality (data are distributed as a multivariate Gaussian distribution); and (3) homescedasticity (residuals of all regressions have zero mean and constant variance). If these assumptions do not hold, users may consider using transformations of the input data or use non-linear instead of linear regression (see Support Protocol 2).

This protocol gives instructions on loading the dataset, defining the model structure, and testing the conditional independencies implied by a DAG with linearly related continuous variables. We use a flow cytometry dataset from a cellular signaling study (Sachs, Perez, Pe'er, Lauffenburger, & Nolan, 2005) as an example. While the goal of this study was to use a structure learning algorithm to automatically learn the causal influences in cellular signaling networks, the authors also presented a “consensus network” representing the current biological knowledge about the signaling pathways. This protocol will show how this consensus network can be tested for its consistency with the data gathered by the authors.

Note that the data used in this protocol are a logicle-transformed (Parks, Roederer, & Moore, 2006) version of the original dataset, since data originating from flow cytometers are not normally distributed. For more details on this transformation, please refer to Support Protocol 2.

Necessary Resources

Hardware

Any computer that can run R and a web browser

Software

• Web browser: any major standards-compliant browser
• Operating system: any operating system that can run R and a web browser
• R: version 3.6 or higher
• R package ‘dagitty’ version 0.3.0 or higher

Files

protein-signal.csv (download dataset at: https://github.com/ankurankan/2020-dagitty-manual/)

1.Open R and load the dagitty package.

• library( dagitty )

2.Import the dataset into R.

• data <- read.csv( file="protein_signal.csv", header=TRUE )

Since the example data file is in csv format, we are using the read.csv function. The file argument specifies the name of the data file; header = TRUE specifies that the first row of the file contains the column names. If you are working with a non-csv format file, please refer to the R documentation for instructions to load it into R.

3.Import the DAG to be tested into R as described in Basic Protocol 1

• model <- dagitty( 'dag {
  • bb="-0.5,-0.5,0.5,0.5"
  • P38 [pos="-0.155,-0.141"]
  • PIP2 [pos="-0.337,0.063"]
  • PIP3 [pos="-0.278,-0.068"]
  • PKA [pos="-0.127,-0.200"]
  • PKC [pos="-0.111,-0.287"]
  • Erk [pos="-0.061,-0.001"]
  • Akt [pos="-0.115,0.052"]
  • Jnk [pos="-0.208,-0.149"]
  • Plcg [pos="-0.337,-0.177"]
  • Mek [pos="-0.063,-0.096"]
  • Raf [pos="-0.066,-0.204"]
  • PIP2 -> PKC [pos="-0.485,-0.379"]
  • PIP3 -> PIP2
  • PIP3 -> Akt
  • PIP3 -> Plcg
  • PKA -> P38
  • PKA -> Erk
  • PKA -> Akt
  • PKA -> Jnk
  • PKA -> Mek
  • PKA -> Raf
  • PKC -> P38 [pos="-0.166,-0.227"]
  • PKC -> Jnk [pos="-0.188,-0.258"]
  • PKC -> Mek [pos="-0.021,-0.245"]
  • PKC -> Raf
  • Plcg -> PIP2
  • Plcg -> PKC [pos="-0.248,-0.271"]
  • Mek -> Erk
  • Raf -> Mek
  • }' )

The imported model can be plotted in R using plot(model) to verify the structure. The plot for the model defined above is shown in Figure 5.

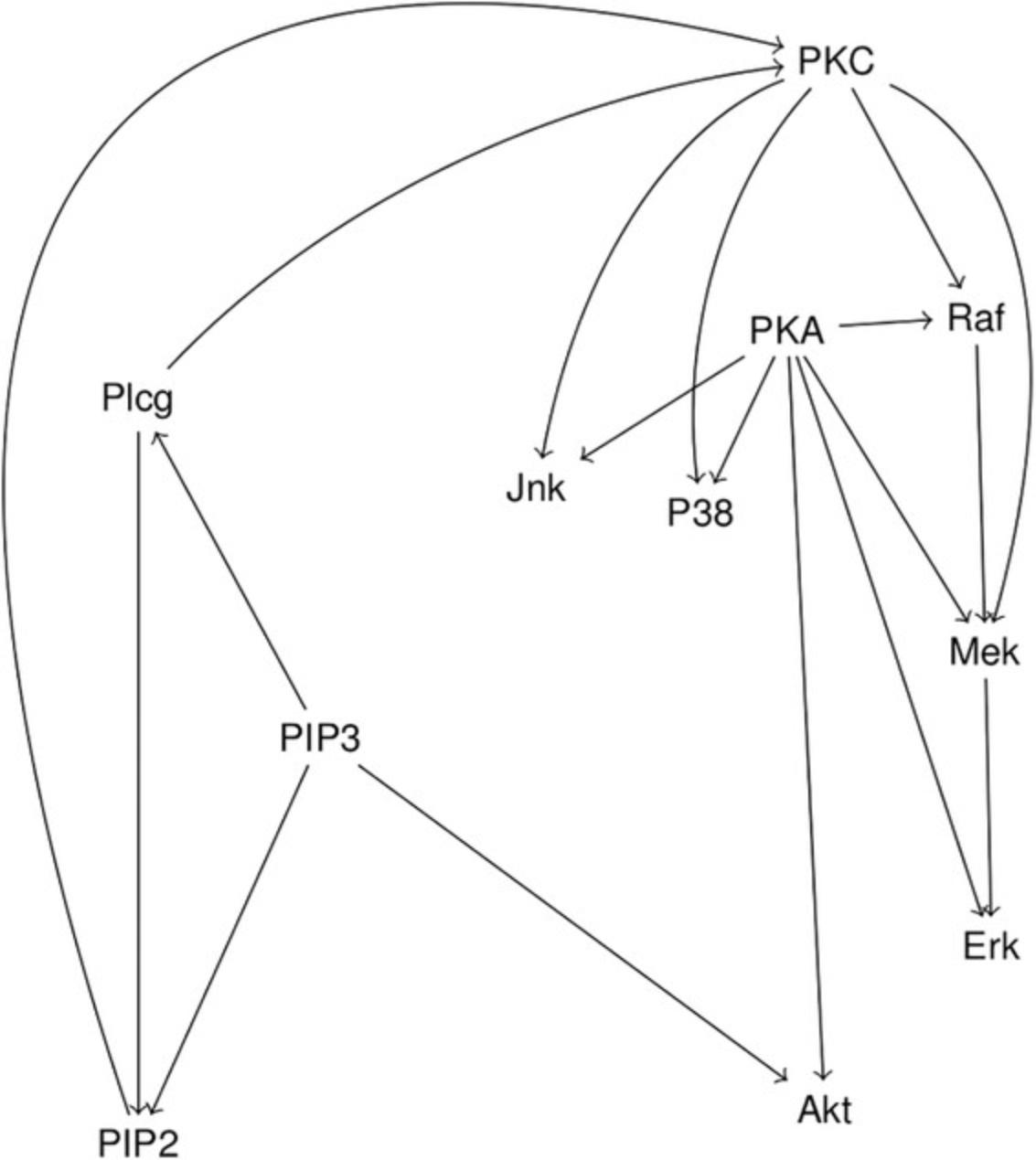
4.After defining the model and importing the data, use the localTests function to test whether all the implied conditional independencies of the model hold in the data.

• res <- localTests( x=model, data=data, type="cis" )
• print( res )

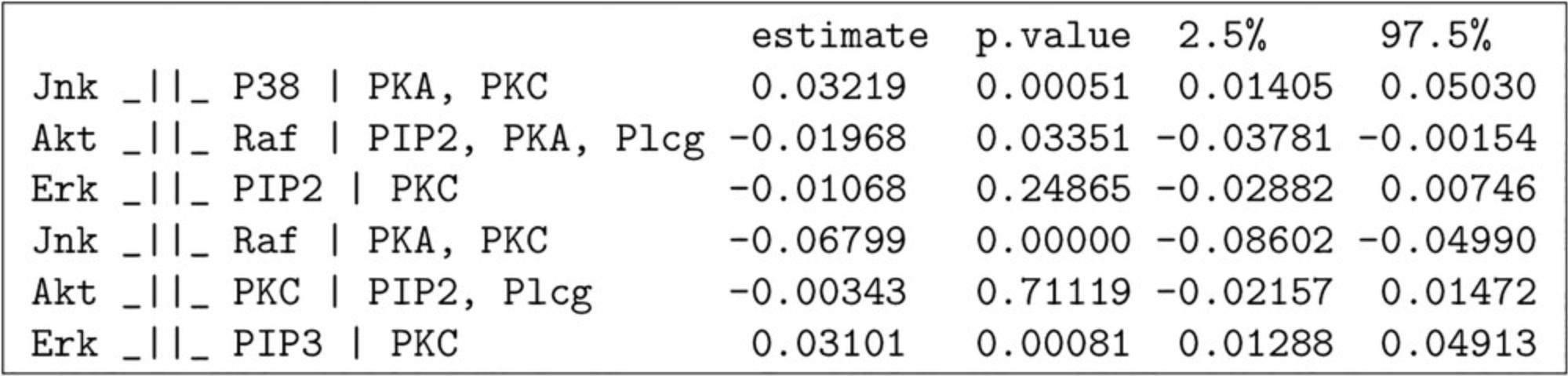
The output of localTests is shown in Figure 6.The localTests function requires the model and data to be specified. Additionally, users can specify the test type. In the case of continuous data, to use the linear-regression based test, the type argument should be specified as cis.

The localTests function outputs the Pearson correlation coefficient, p -value, and confidence interval of the correlation coefficient for each of the conditional independencies implied by the model structure. The Pearson's correlation coefficient varies between −1 and 1, with 0 implying no correlation and −1 or 1 implying a perfect linear correlation. The p -value for the test indicates the probability of observing the given dataset under the hypothesis that the independence condition is true. Hence, a correlation coefficient of around 0 with a high p -value (>0.05) is typically observed if the conditional independence holds in the data. By contrast, a high value of the correlation coefficient with a low p -value suggests that the conditional independence does not hold in the dataset. The 2.5% and 97.5% columns indicate the 95% confidence interval for the correlation coefficient; the more narrow the confidence interval and the further it is away from zero, the stronger the evidence that conditional independence does not hold.

5.Optional : Test only some of the implied conditional independencies.

• res <- localTests( x=model, data=data,
  • max.conditioning.variables=2 )
• print( res )

In the case that we do not wish to test all the implied conditional independencies of the model, the max.conditioning.variables argument of localTests allows users to specify a subset of independencies to test. In the example above, only independence conditions with less than 3 conditional variables are tested.

6.Optional : Plot test results using the plotLocalTestResults method to visually inspect the correlation coefficient and its confidence interval. This can be useful if there are many test results to consider. Here, we will generate a plot that will focus on the 20 most problematic test results (i.e., the ones for which the effect sizes are the furthest way from 0).

To do this, we first sort the test results by their effect size:

• res <- res[order( abs( res$estimate ) ),]

Next, we plot the 20 results with the largest effect size:

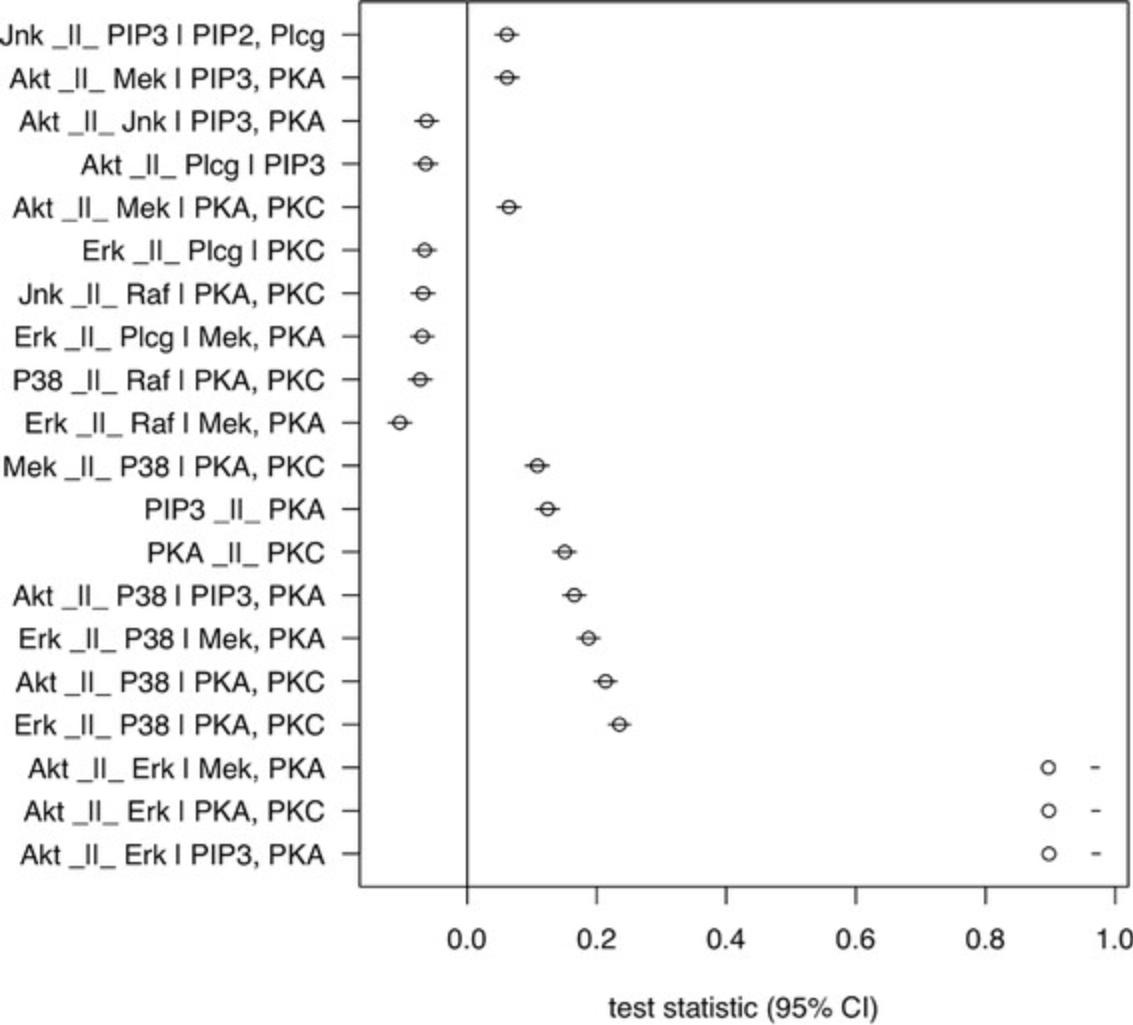
• plotLocalTestResults( tail( res, 20) )

The resulting plot shows the point estimate of the correlation coefficient along with its confidence interval for each conditional independence tested (Fig. 7). From the result, it is very clear that the independence between the Akt and Erk protein, which is implied by the consensus network, is very strongly contradicted by the data with effect sizes of more than 0.9. Although there are other violations of independence implications, those are far more modest in comparison. For more details on interpreting these results, refer to Guidelines for Understanding Results.

In the previous protocol for testing the model against continuous data, we used a linear regression-based test that is only valid when the relationship between the variables is approximately linear. In this protocol, we describe methods for testing conditional independencies against continuous data when the relationship between variables is not linear. There are, broadly, two approaches to such situations: (1) transform variables to a different scale, on which relationships become linear; (2) employ non-linear regression techniques. Since the choice of data transformation is highly dependent on the distribution of the dataset, we suggest that readers refer to the relevant literature for commonly used transformations for a specific type of dataset. Here, we show examples of using: (1) the log transformation, a very common general-purpose transformation applied to data that is approximately log-normally distributed; and (2) the logicle transformation (Parks et al., 2006), a biexponential transformation that is frequently applied to flow cytometry data of the type used in Basic Protocol 2.For the non-linear regression, we describe the method using LOESS (Locally Estimated Scatterplot Smoothing; Cleveland, 1979).

Necessary Resources

• This protocol has the same prerequisites as Basic Protocol 3 and assumes that users have already performed steps 1-3 of that protocol to load their data and model into R. In addition, step 2 of this protocol requires the R package ‘premessa’ and the Bioconductor package ‘flowCore’. Please see https://github.com/ankurankan/2020-dagitty-manual/ for installation instructions.

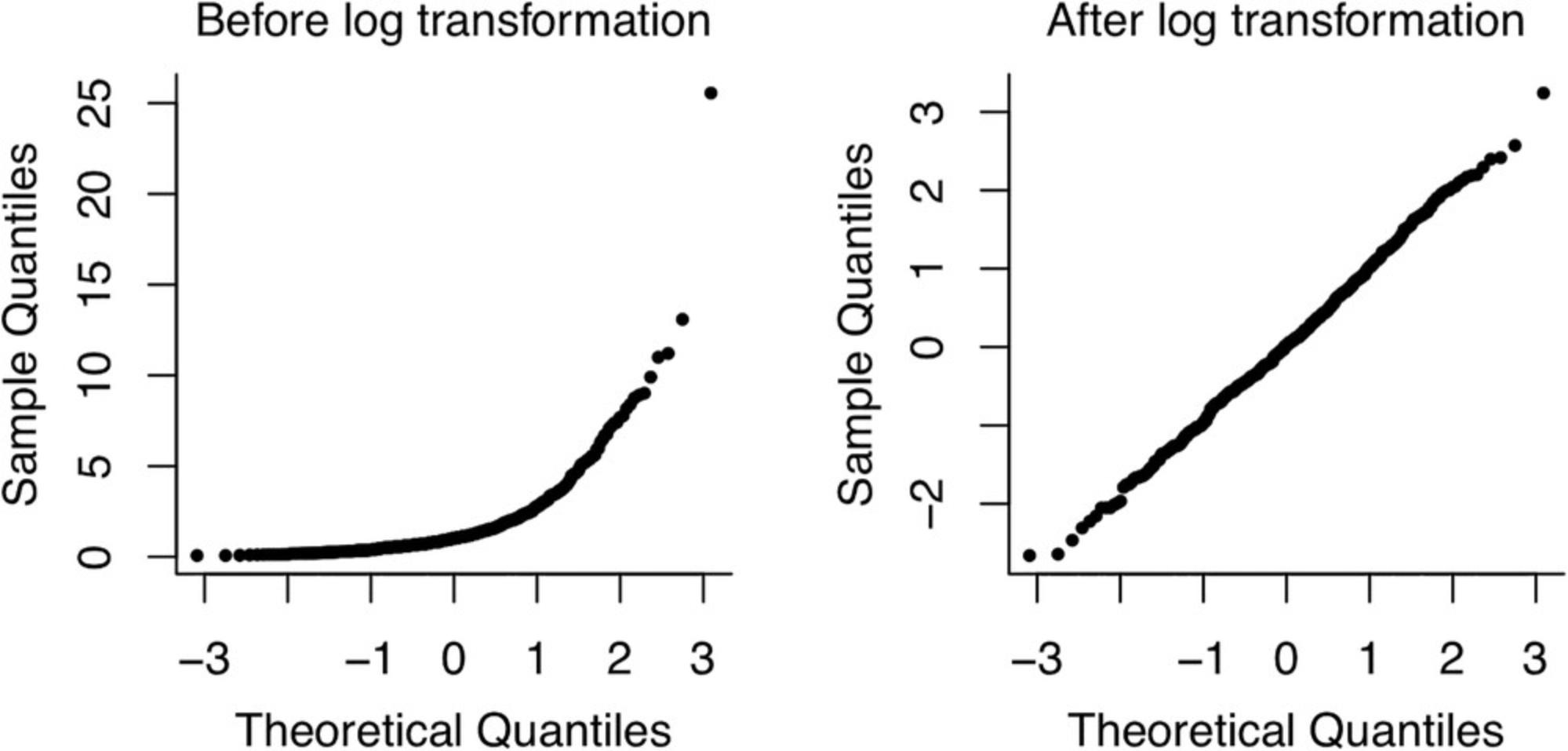
1.Optional : Log-transform one or more of the variables such that non-linear variable relations become approximately linear after transformation. Variables can be transformed if they have log-normal distributions (such that the transformed variable is normally distributed and fulfills the normality condition of linear regression). The quantile-quantile plot (QQ plot) is a useful tool to assess normality of a variable and its log-transformed version. Normally distributed data roughly follow a straight line on a QQ plot. When the data instead have a log-normal distribution, the QQ plot looks more similar to a parabola. When log transformation succeeds in making the distribution of a variable approximately normal, the QQ plot of the transformed variable should be approximately linear (Fig. 8).

As an example, we show the effect of log-transformation on a simulated log-normally distributed variable.

• X <- rlnorm( 500 )
• par( font.main=1, cex.main=1, bty='l',
  • mfrow=c( 1, 2 ), pch=19, mar=c( 4, 4, 2, 1 ) )
• qqnorm( X, main="Before log transformation", cex=.5 )
• qqnorm( log( X ), main="After log transformation", cex=.5 )

The code snippet above first generates 500 random samples from a log-normal distribution with mean 0 and standard deviation 1 on the log scale. The par function sets the parameters for our plot, and then we plot the qqplots for the variable “X” and its log-transformed version.

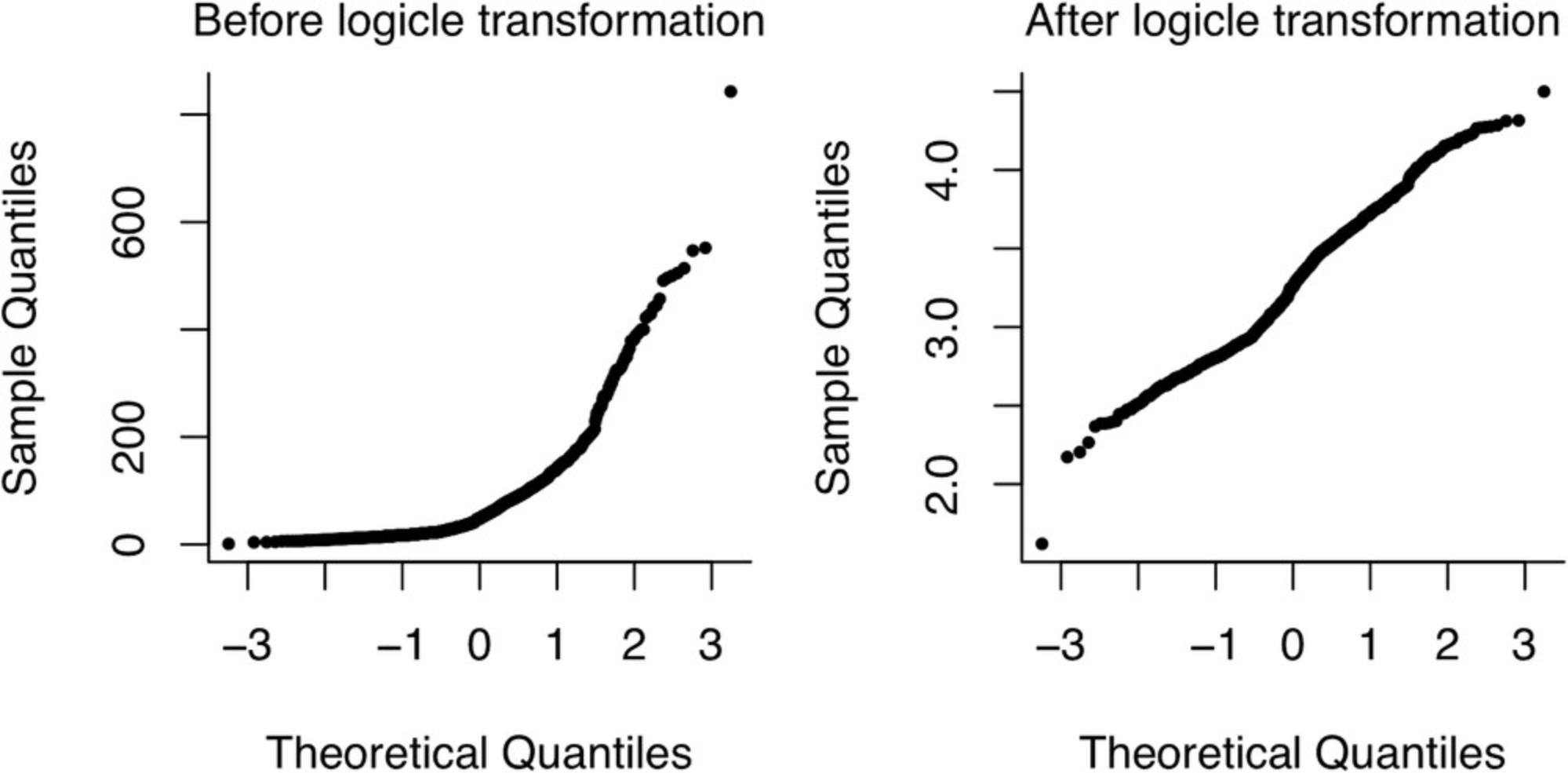
2.Optional : The logicle transformation (Parks et al., 2006) is commonly applied to flow cytometry datasets. Data from flow cytometry are often roughly log-normally distributed, making log-transformation a possible alternative. However, the signal from flow cytometers actually follows a more normal distribution for small values and only becomes log-normal for large enough values. Furthermore, spillover compensation can make some of the values negative, such that log transformation can no longer be applied. Logicle transformation solves these problems by doing asymptotic linear transformation near 0 values and asymptotic log transformation at higher (positive or negative) values. The transformation is actually parametric, but its two parameters are typically estimated from the data at hand.

In the example below, we use the implementation of logicle transform from the Bioconductor R package flowCore (Ellis et al., 2019).

• library( readxl )
• library( flowCore )
• library( premessa )
• dataset <- as.matrix( read_excel( "cd3cd28.xls" ) )
• d_flow <- as_flowFrame( dataset )
• lgcl <- estimateLogicle( d_flow,
  • channels=colnames( d_flow))
• d_trans <- exprs( transform( d_flow, lgcl ) )
• par( font.main=1, cex.main=1, bty="l",
  • mfrow=c( 1, 2 ), pch=19, mar=c( 4, 4, 2, 1 ) )
• qqnorm( dataset[, 4], main="Before logicle transformation", cex=.5 )
• qqnorm( d_trans[, 4], main="After logicle transformation", cex=.5 )

In the code snippet above, we start with the loaded dataset d_flow, and then first convert it to a flowFrame object using the as_flowFrame function from the package premessa. We then estimate the parameters for the logicle transformation using the estimateLogicle function. The estimateLogicle function accepts the channels argument to specify the variables to transform. The transform function then applies the transformation with the estimated parameters on the data. In Figure 9, we show the effect of the transformation on one of the variables of the flow cytometry dataset from Sachs et al. (2005).

3.Optional : Use LOESS. In some cases, the non-linear relationship is more complex and a data transformation does not suffice to make it linear. In these cases, users can compute regression residuals with LOESS rather than linear regression. LOESS fits simple models to localized subsets of data to build a (non-linear) fitting function that describes the deterministic part of variation in the data.

To use LOESS for testing, the type parameter needs to be specified as cis.loess:

• localTests( myDAG, data, type="cis.loess",
  • R=100, max.conditioning.variables=4 )

In this case, the confidence interval of the estimate is computed using bootstrapping, which is controlled by an additional parameter R giving the number of bootstrap replicates. Additional parameters for LOESS can also be specified in localTests by passing them to the loess.pars argument. A restriction of using this method is that the implementation works only for conditional independencies with less than 5 conditional variables. Hence, the implied conditional independencies will need to be filtered using the parameter max.conditioning.variables before testing them.

The previous protocols described DAG testing in cases where the dataset contained either only categorical or only continuous variables. In this protocol, we show how to test models against datasets containing both categorical and continuous variables. This method involves computing the so-called polychoric correlation (Pearson, 1900) matrix of the dataset, which is used to test whether the implied conditional independencies of the model hold in the data. When we compute the polychoric correlation, we assume that each of the categorical variables in the dataset has been derived by “binning” some underlying “latent” variable, which we assume is continuous and normally distributed. For example, assume we have in our dataset a categorical variable education level with the categories Non-HS-Grad , HS-grad , College-Associate , Academic-Degree. We can then assume that each person's education level has an underlying continuous distribution, where people with similar education levels have the same graduation or degree. This underlying education level is then a “latent” continuous variable (that is, we do not observe it directly), which we can use for our polychoric correlation.

This approach works for so-called ordinal categorical variables, where the categories have a natural ordering (e.g., from low to high). Yet the dataset may also contain variables that are non-ordinal (e.g., “color,” where there is no natural ordering of “red,” “blue,” and “yellow”). Polychoric correlation works with continuous and ordinal variables, and can also be used with binary variables because binary variables can be given an arbitrary ordering. The approach cannot directly incorporate categorical variables with more than two levels. If there are few such variables, users could decide to forego testing conditional independencies that involve them, or consider merging some of the categories to allow them being tested to some extent.

To illustrate the polychoric correlation technique, we chose a dataset that is easy to interpret for readers from different backgrounds rather than a specific bioinformatics dataset as in the previous protocol. This choice will allow us to focus on the actual technique rather than the specific nature and meaning of the data. For this purpose, we use the “adult income” dataset (Kohavi, 1996) available at the UCI machine learning repository (Dua & Graff, 2019). We will show the required preprocessing steps for both ordinal and non-ordinal variables, computing the polychoric correlation matrix, and then testing it with our model structure. For simplicity, we have pre-processed the dataset by merging and cleaning some variables, and provide the cleaned version as a supplementary csv file, adult.csv.

Necessary Resources

Hardware

Any computer that can run R and a web browser

Software

• Web browser: any major standards-compliant browser
• Operating system: any operating system that can run R and a web browser
• R: version 3.6 or higher
• R package ‘dagitty’ version 0.3.0 or higher
• R package ‘lavaan’ version 0.6 or higher

Files

adult.csv (download dataset at: https://github.com/ankurankan/2020-dagitty-manual/)

1.Open R and load the dataset.

• data <- read.csv( "adult.csv" )

2.Define the ordinal categorical variables. The categories of Age , Education , HoursPerWeek , and Income in our dataset have a natural ordering, hence they are defined as ordinal variables.

• dataAge,
  • levels=c( "<20", "20-34", "35-49", "50-65", ">65" ) )
• dataEducation,
  • levels=c( "Non-HS-Grad", "HS-grad",
  • "College-Associate", "Academic-Degree" ) )
• dataHoursPerWeek,
  • levels=c( "<20", "20-39", "40", ">40" ) )
• dataIncome,
  • levels=c( "<=50K", ">50K" ) )

3.Define binary variables. The rest of the variables in the dataset are binary and we will convert them to integers. This will assign an arbitrary order to each variable: the lexicographically smaller value will be assigned a 1, and the larger value a 2.For example, the variable “Immigrant” has the values “no” and “yes,” so “no” will be translated to 1 and “yes” to 2.

• dataRace )
• dataSex )
• dataImmigrant )

4.Optional : Deal with non-ordinal categorical variables with more than 2 categories. In the last step, we defined the non-ordinal variables with two categories as binary but this does not work for variables with more than 2 categories, and they need to be dummy encoded. In our dataset, we have the variable Marital Status with the categories: Is-Married , Never-Married , Was-Married. We decide to merge the two categories Never-Married and Was-Married into a single category and rename the resulting two categories, which can be accomplished as follows:

• levels(data$MaritalStatus) <- list(
  • Married="Is-Married",
  • NotMarried=c( "Was-Married", "Never-married" ) )

Then we convert this variable to a binary number like previously:

• dataMaritalStatus )

Here, 1 will now mean “Married” and 2 will mean “Not Married.”

5.Compute the correlation matrix. We can use the lavCor function implemented in the lavaan package to compute the polychoric correlation matrix from the dataset as:

• library( lavaan )
• corr <- lavCor( data )

In the current version of lavaan (0.6), the function lavCor gives a warning message: “estimation of the baseline model failed.” This warning can be safely ignored.

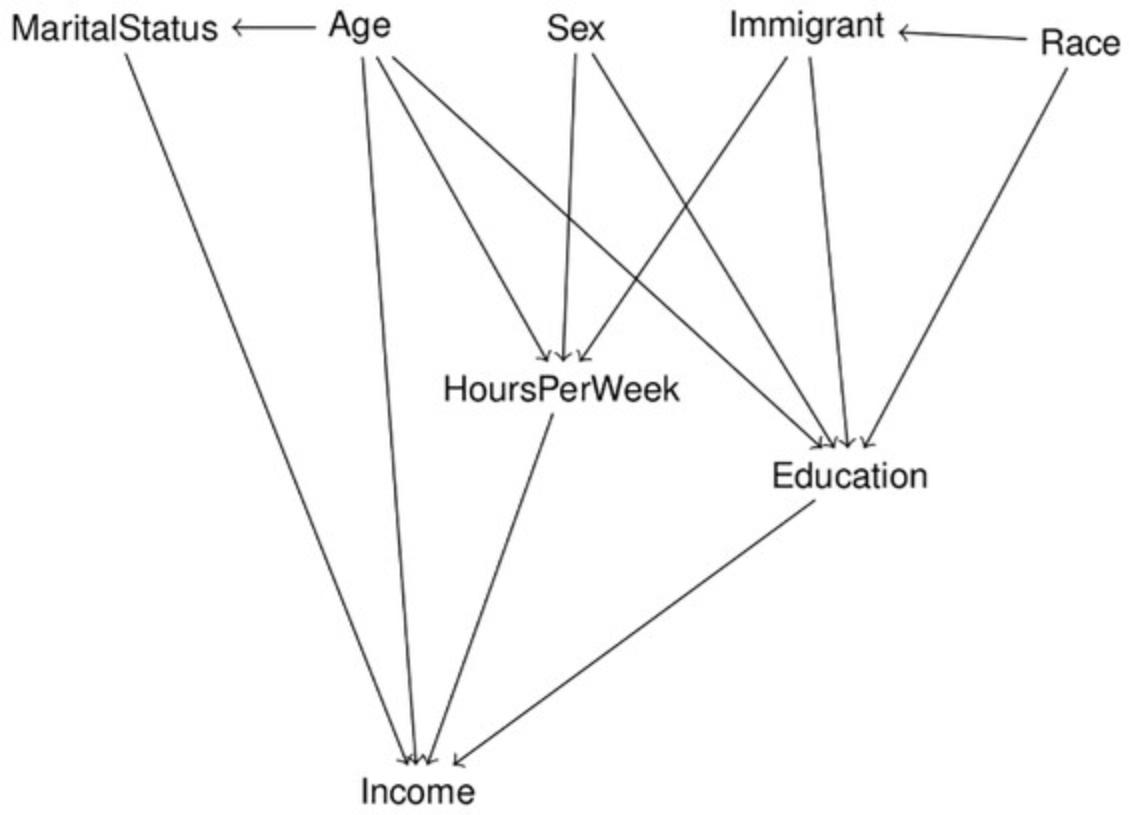
6.Create the model structure. We can use the dagitty web interface to create the model structure and import it to R as shown in Basic Protocol 1.Below, we directly give an abbreviated DAG code for reference.

• library( dagitty )
• model <- dagitty( 'dag {
  • bb="-4.6,-3.8,3.7,3.7"
  • Age [pos="-2,-2.6"]
  • Education [pos="1.4,0.5"]
  • HoursPerWeek [pos="-0.6,-0.1"]
  • Immigrant [pos="1.1,-2.6"]
  • Income [pos="-1.6,2.7"]
  • MaritalStatus [pos="-3.7,-2.6"]
  • Race [pos="3.0,-2.5"]
  • Sex [pos="-0.5,-2.6"]
  • Age -> { Education HoursPerWeek Income MaritalStatus }
  • Education -> Income
  • HoursPerWeek -> Income
  • Immigrant -> { Education HoursPerWeek }
  • Immigrant <-> Race
  • MaritalStatus -> Income
  • Race -> Education
  • Sex -> { Education HoursPerWeek }
• }' )

The imported model can be plotted in R using plot( model ) to verify the structure. The plot for the model defined above is shown in Figure 10.

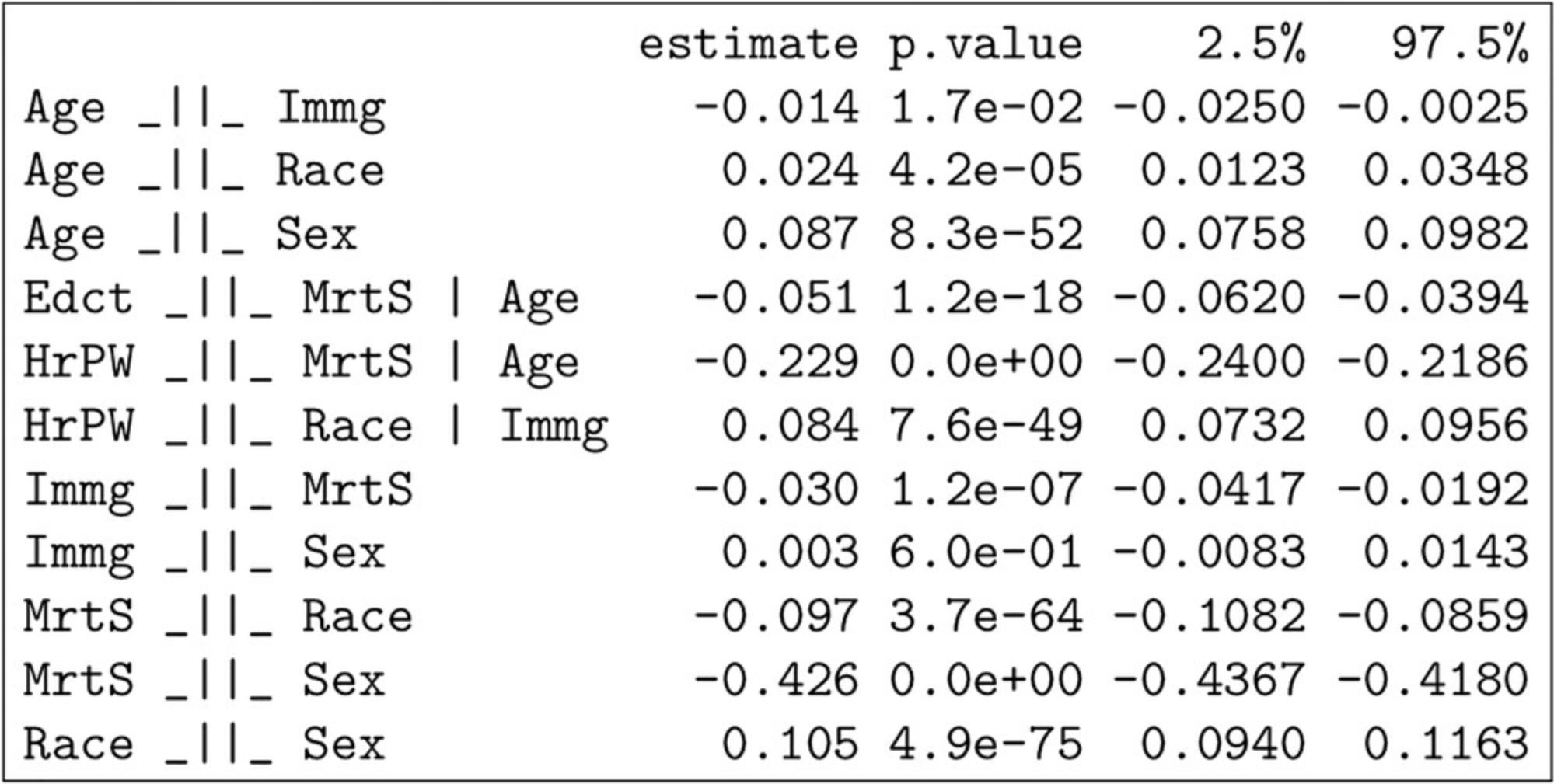
7.Test the implied conditional independencies of the model structure against the correlation matrix.

• localTests( model, sample.cov=corr, sample.nobs=nrow( data ) )

The output of localTests is shown in Figure 11. When testing using the sample covariance matrix, localTests returns an estimate, the p -value of the test, and the confidence interval for the estimate. An estimate of around 0 with a p -value higher than 0.05 would mean that the data do not provide evidence against the implied conditional independence being tested. Note that there is a strong negative relationship between being female and being married, indicating a major bias in the collection of this dataset.

8.Optional : Test only some of the implied conditional independencies.

• localTests( x=model, sample.cov=corr,
  • sample.nobs=nrow( data ),
  • max.conditioning.variables=2 )

In the case that we only want to test some of the implied conditional independencies of the model, the tests argument of localTests allows users to specify a subset of the independencies to test. In the example above, only independence conditions with less than 3 conditional variables are tested.

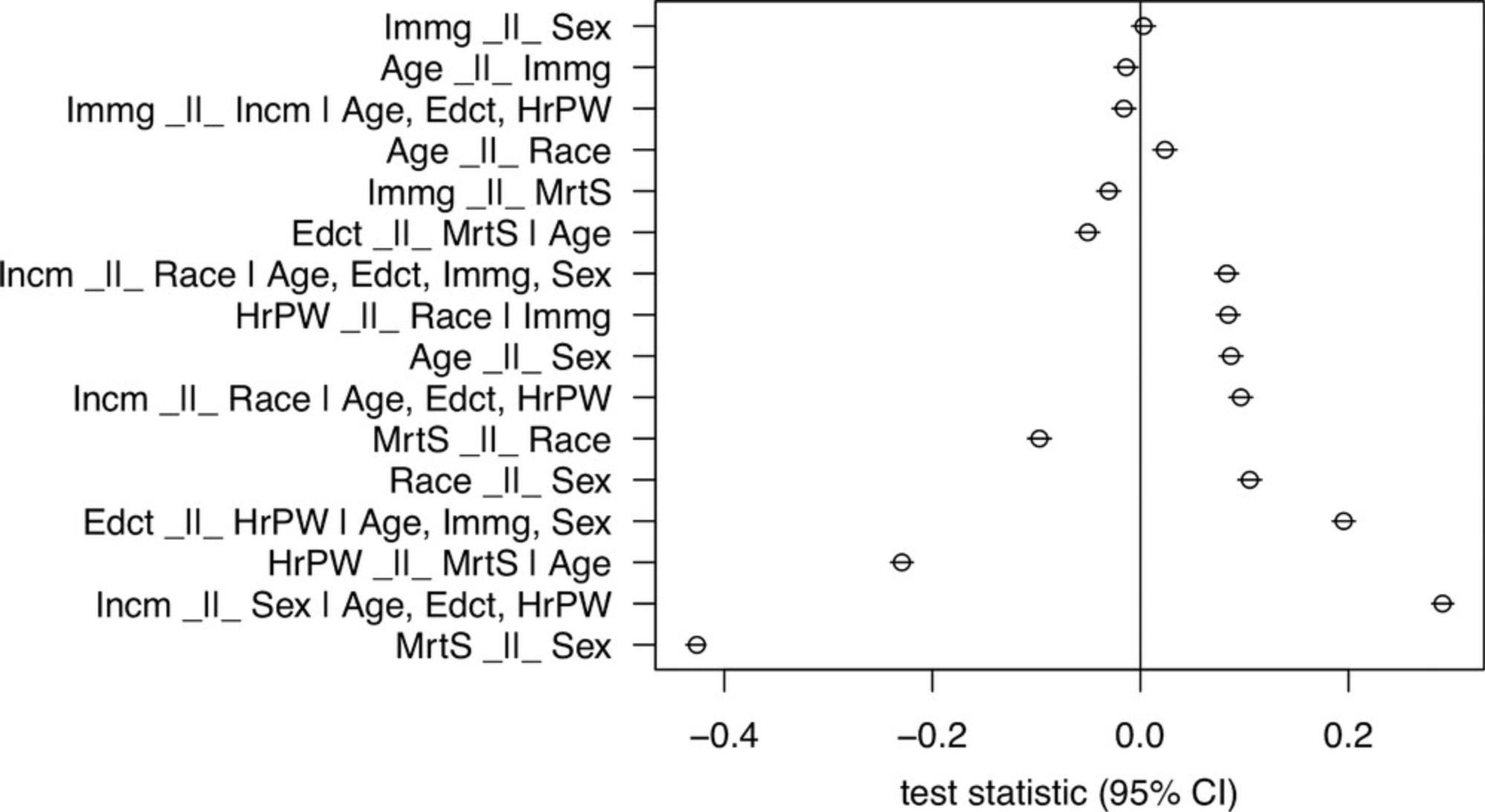
9.Optional : Plot the test results.

• plotLocalTestResults( localTests( model,
  • sample.cov=corr, sample.nobs=nrow( data ) ) )

Similar to the previous protocols, all the test results can be plotted to inspect the results visually. An example output is shown in Figure 12.

The statistical basis of testing DAG models is given by the conditional independences implied by the model. Dagitty computes these automatically based on so-called d-separation statements from this DAG. For background information on the logic of d-separation and conditional independence testing, we recommend studying the corresponding chapters in the textbook “Causal Inference in Statistics: A Primer” (Pearl, Jewell, & Glymour, 2016). We have also explained these concepts in the context of linear-Gaussian models (Thoemmes et al., 2018).

Our protocols differ in the type of data used and the conditional independence test applied, but ultimately each protocol uses the function ‘localTests’ to perform the actual testing. This function always returns a table with the following pieces of information:

• An effect size. For linear tests (Basic Protocols 3 and 4), this is a (partial) correlation coefficient. For the chi-square test (Basic Protocol 2), we use the root mean square error of approximation (RMSEA).
• A confidence interval for the effect size. This confidence interval is by default computed through analytical approximations, but the parameter ‘R’ can be used to instead bootstrap the confidence interval (which involves computing the effect size on different subsamples of the data, and then seeing how this estimate varies as a measure of uncertainty).
• A p -value for the hypothesis that the effect size is 0 (i.e., (conditional) independence of variables).

More details can be added depending on the exact test used, such as the degrees of freedom for a chi-square test.

Users should not rely on p -value alone to conclude whether a tested independency holds in the data or not. In large datasets, the association between two variables is rarely exactly 0, which may yield small p -values even for negligible “associations.” Users should therefore take into account some measure of the effect size to decide if a detected association requires a change in the model (similar to how we may choose to ignore a correlation of 0.0001, even if it comes with a “significant” p -value of 0.01).

Unfortunately, the effect size in a chi-square test is difficult to quantify. Note that when two categorical variables X and Y fall into categories or levels x ₁, …, x_n and y ₁, …, y_m , their distribution can be written in the form of a n × m contingency table where each entry [i ,j] counts how many datapoints have values X = x_i and Y = x_j. The chi-square test then compares these observed counts with the expected counts that we would get if the two variables were independent of each other (in that case, we would expect the relative frequencies to be the same between all rows and between all columns). The χ² test statistic measures how much the “observed” table deviates from the “expected” one. However, χ² is a poor measure of effect size because it varies strongly with sample size. The localTests() function, therefore, also returns the RMSEA (Root Mean Square Error of Approximation), which is a normalized version of χ². Larger RMSEA values indicate a larger effect size. Unfortunately, unlike the correlation coefficient, the RMSEA has no upper bound and its value still depends on the size n × m of the contingency table [also reflected by the degrees of freedom, df = (n − 1) × (m − 1)]. RMSEA values below 0.05 are often considered acceptable—but this strongly depends on the context and on the degrees of freedom of the test. We can, therefore, impossibly come up with a single threshold below which users can safely regard the RMSEA as negligible. Instead, we recommend users to start improving the model for the tests with the highest RMSEA values, and to use their domain knowledge to decide at what point the model has been sufficiently improved to capture the data.

It is important to point out here that this type of testing does exactly the opposite of a classical null hypothesis significance test (NHST), which readers may be more familiar with. In an NHST, we aim to reject the null hypothesis. For instance, when comparing a group of drug-treated patients to another group given a placebo, the null hypothesis is that the drug has no effect. Thus, an effect size of 0 would be considered a negative outcome.

Testing DAGs is different because all conditional independencies implied by a DAG require the associated effect size—the conditional dependence—to be 0. Thus, every effect that is numerically close to 0 corroborates the assumptions encoded in the DAG, and is therefore the desired outcome. By contrast, large and statistically significant effects may signify that something is wrong with the model or data. In teaching, we have frequently observed that students struggle with this and mistakenly interpret a zero effect size as a sign that something is wrong with the DAG, while in fact it implies the exact opposite.

The function plotLocalTestResults is designed to help interpret the test results correctly. Ideally, all effect sizes (points) should fall onto the 0 line. The further the effect size is from that line, the stronger the evidence against the corresponding implication of the DAG. As always in statistical analysis, it is important to also consider the uncertainty associated with the effect size estimate, so the confidence intervals are also displayed. An effect size that is far from 0 with a narrow confidence interval is difficult to reconcile with the corresponding conditional independence implication. In such a case, changes to the DAG model should be considered.

As with any statistical model, performing too many post-hoc changes to a DAG runs the risk of “overfitting” the DAG to the specific dataset the tests are being performed on. General techniques to prevent overfitting include splitting the dataset in two random parts and performing p -value multiple testing adjustments (see below) to gauge how many failed tests would be consistent with chance alone. We would strongly recommend that users not base any changes made to a DAG model only on the data, but also keep in mind that there should be a firm theoretical basis for the revised DAG structure.

In the case of a failed conditional independence test X ⊥ Y |Z , the DAG can always be “repaired” by adding an edge between X and Y , and indeed this is the most common modification performed in practice. However, there are many more reasons why a test could fail, including but not limited to the following:

• There could be an important difference between a variable in the DAG and the actual measurement of that variable. For example, when building DAGs, researchers often think in terms of longitudinal processes, but the variables measured in a cross-sectional dataset might not reflect those processes well.
• One or several of the variables in Z could be affected by measurement error.
• There could be an unobserved common cause between X and Y.
• Some of the arrows leading from X to Y via Z could go into the wrong direction.

We strongly encourage readers to consider these and other possible explanations when making modifications to their models. In general, users should not expect model testing to quickly yield a revised, better model. Developing good models is a slow, iterative process that involves cycles of theorizing, challenging the theory against data, finding discrepancies in the theory, improving the theory, and challenging it again using new data. From that perspective, the current practice to construct “one-off” causal diagrams specifically for the analysis of one given dataset (Tennant et al., 2020) appears unlikely to yield good DAG models.

In many cases, discrepancy between a DAG and a dataset could also point to an error in the dataset rather than the DAG itself. An example is shown in Basic Protocol 4. There is good reason to believe that marital status and sex should be independent in this dataset: it was collected in the United States during a time when every marriage included one man and one woman. Therefore, in a random sample of the population, the percentage of married men and women should be roughly equal. In this dataset, the percentage of married men is, however, much higher than the percentage of married women. It, therefore, appears likely that this dataset is heavily skewed, possibly by including an extra batch of high-earning people, which were overwhelmingly married men at the time when the data were collected.

Background Information

Carefully controlled experiments are considered the gold standard when it comes to establishing cause-effect relationships in nature. Yet, experimentation is not always feasible or even desirable. For example, it is commonly accepted that exposure to asbestos can be a cause of cancer, but this cannot be established in an experimental setting—because this would require people to be exposed to asbestos on purpose. In many fields, such as econometrics or epidemiology, causal inference relies primarily on the analysis of observed data “from the real world” instead of controlled experiments. Also, molecular biologists frequently attempt to draw causal conclusions from observational data, for example, when analyzing blood or tissue samples from cohorts of cancer patients in an attempt to find mechanistic clues for the development of the disease or lack of response to a therapy.

The field of causal inference is concerned with the development of formal methodology that aims to establish causal insight from non-experimental data (or a mix of experimental and observational data). The interest in causal inference has increased substantially in the past two decades, and especially in the past few years due to the publication of Judea Pearl's “Book of Why” (Pearl & Mackenzie, 2018), which explains the subject in a widely accessible manner.

A key insight in causal inference is that establishing cause-effect relationships from observational data always requires making assumptions that are not statistical, but mechanistic in nature. Without such extra assumptions, we cannot really distinguish between correlation and causation: the fundamentally asymmetric characteristics of “cause” and “effect” in any process generating observed data are lost when we look only at associations between variables, which are symmetric (the correlation of variable A with B is the same as of B with A). Sometimes this fundamental problem of causal inference can be solved by clever experimental design, such as in a randomized controlled trial, where we can guarantee by design that improvements observed in the patient outcome must be due to the treatment and not due to confounding factors. When such experimental designs are not feasible, we instead need to make other assumptions on the data-generating process.

One approach to encode such assumptions is by using directed acyclic graphs (DAGs), which graphically depict the hypothesized causal relationships. DAGs are essentially networks of variables which we assume have an important influence on the data we see, and which may or may not be measured. But aside from a graphical depiction of causal relationships, a DAG is also a mathematical model that can be analyzed. Importantly, a DAG can inform us whether, and how, we would be able to identify a causal effect in observational data if the assumptions encoded in the DAG would hold. Since the correctness of the conclusions of a DAG-based analysis obviously depends on the correctness of the underlying DAG, it would appear desirable to subject DAGs to extensive scrutiny before using them to analyze data. Surprisingly, a recent review of the practical use of DAGs in health research did not find a single case where the authors tested the DAG they built—among more than two hundred articles (Tennant et al., 2020).

With these protocols, we therefore aimed to provide clear step-by-step instructions to help researchers test their models. We based this procedure on the simplest possible ways we could think of to test against linear and categorical data, which are based on statistical techniques (linear regression and the chi-square test, respectively) that we expect many readers to be familiar with. We have also included a slightly more advanced protocol to illustrate how a more advanced statistical technique (polychoric correlation; Basic Protocol 4) can be harnessed for DAG testing. In general, we emphasize that these protocols should not be seen as the exclusive or only way to test DAG models. In fact, conditional independence testing is still a highly active research topic, with new tests being constantly developed. The R package ‘CondIndTests’ (Heinze-Deml, Peters, & Meinshausen, 2018) implements more advanced methodology for conditional independence testing, based on kernel methods and other approaches. We would recommend readers to thoroughly familiarize themselves with the theory underlying these more advanced approaches before using them.

Critical Parameters and Troubleshooting

Two important parameters that need to be considered in testing DAG implications are the number of the implications that are tested and the complexity of each implication. The two parameters are interrelated. First, while small DAGs might only have a few, a single, or even no testable implications, more complex DAGs such as the one in Basic Protocol 3 can have dozens or even hundreds of implications. With such large numbers of statistical tests, the multiple testing problem needs to be kept in mind. That is, even if all implications of the DAG were correct, we would still expect a certain fraction of the tests to fail (produce low p -values) just by chance. To get a better idea of how many failed tests are expected, the procedure explained in our protocols can be combined with p -value adjustments such as the Bonferroni-Holm or Benjamini-Hochberger procedures, as implemented in the R command p.adjust.

The complexity of a conditional independence test depends on the number of variables that need to be conditioned on. When this number is high, conditional independence tests can become statistically unreliable. This is especially an issue with categorical data and the chi-square test. This test essentially subdivides the dataset into as many pieces as there are unique combinations of the values of the variables that we condition on. For example, when conditioning on 10 binary variables, then we would have 2¹⁰ = 1024 possible combinations. In a dataset with 1000 rows, for instance, this might mean that we have just a single observation for the vast majority of the possible combinations of the conditioning variables. It is of course impossible to conduct a chi-square test on a single observation, and the results for small numbers of observations are unreliable. Therefore, great caution should be taken when interpreting such results, and depending on the size of the dataset, it might be best to altogether avoid tests of a certain complexity.

One way to detect potentially unreliable tests is to use the bootstrapping functionality of the localTests function (parameter R). If the bootstrapped confidence intervals deviate greatly from the analytical approximations, or if these confidence intervals are much wider than the analytical ones, this is an indication that the statistical assumptions underlying the tests are not met. Results from such unreliable tests should not be the basis for any subsequent modifications of the DAG.

When encountering unreliable test results, we suggest to focus on the results of more reliable tests, if these are available. Typically, those will be tests where we condition on fewer variables (for example, at most 1 or 2). Basic Protocol 2 contains instructions for how to limit the number of conditioning variables that are considered. This also helps to reduce the number of tests that are performed.

Author Contributions

Ankur Ankan : Conceptualization; Methodology, writing-original draft, writing-review & editing. Inge M. N. Wortel : Conceptualization; Methodology, writing-original draft, writing-review & editing. Johannes Textor : Conceptualization; Methodology, writing-original draft, writing-review & editing.

Funding Information

Inge M. N. Wortel was supported by a Radboudumc Ph.D. grant. Johannes Textor and Ankur Ankan were supported by a Young Investigator Grant (10620) from KWF.

Conflict of Interest

The authors declare no conflict of interest.

Data Availability Statement

Data sharing not applicable–no new data generated.

• Cleveland, W. S. (1979). Robust locally weighted regression and smoothing scatterplots. Journal of the American Statistical Association , 74(368), 829–836.
• Dua, D., & Graff, C. (2019). UCI machine learning repository. Available at http://archive.ics.uci.edu/ml.
• Ellis, B., Haaland, P., Hahne, F., Meur, N. Le, Gopalakrishnan, N., Spidlen, J., … Finak, G. (2019). flowCore: Basic structures for flow cytometry data , R package version 1.52.0.
• Grolemund, G., & Wickham, H. (2020). R for data science. Online e-book. Available at http://r4ds.had.co.nz/#.
• Heinze-Deml, C., Peters, J., & Meinshausen, N. (2018). Invariant causal prediction for nonlinear models. Journal of Causal Inference , 6(2), doi: 10.1515/jci-2017-0016.
• Kohavi, R. (1996). Scaling up the accuracy of naive-bayes classifiers: A decision-tree hybrid. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining , KDD’96, (pp. 202–207). Pao Alto, CA: AAAI Press.
• Parks, D. R., Roederer, M., & Moore, W. A. (2006). A new “logicle” display method avoids deceptive effects of logarithmic scaling for low signals and compensated data. Cytometry Part A , 69(6), 541–551. doi: 10.1002/cyto.a.20258.
• Pearl, J., & Mackenzie, D. (2018). The book of why. New York: Basic Books. ISBN 978-0-465-09760-9.
• Pearl, J., Jewell, N. P., & Glymour, M. (2016). Causal Inference in Statistics: A Primer. Hoboken, NJ: John Wiley & Sons.
• Pearson, K. (1900). I. mathematical contributions to the theory of evolution.—vii. on the correlation of characters not quantitatively measurable. Philosophical Transactions of the Royal Society of London. Series A , 195(262-273), 1–47. doi: 10.1098/rsta.1900.0022.
• Sachs, K., Perez, O., Pe'er, D., Lauffenburger, D. A., & Nolan, G. P. (2005). Causal protein-signaling networks derived from multiparameter single-cell data. Science , 308(5721), 523–529. doi: 10.1126/science.1105809.
• Tantau, T. (2007). Tikz and pgf: Manual for version 1.18. Available at: https://static.yanyin.tech/literature/current_protocol/10.1002/cpz1.45/attachments/tikzpgfmanual.pdf.
• Tennant, P. W., Murray, E. J., Arnold, K. F., Berrie, L., Fox, M. P., Gadd, S. C., … Ellison, G. T. (2020). Use of directed acyclic graphs (DAGs) in applied health research: Review and recommendations. International Journal of Epidemiology , dyaa213. doi: 10.1093/ije/dyaa213[Online ahead of print].
• Textor, J., Hardt, J., & Knüppel, S. (2011). DAGitty: A graphical tool for analyzing causal diagrams. Epidemiology , 5(22), 745. doi: 10.1097/EDE.0b013e318225c2be.
• Textor, J., Zander, B. v. d., Gilthorpe, M. S., Liśkiewicz, M., & Ellison, G. T. H. (2016). Robust causal inference using directed acyclic graphs: The R package ‘dagitty’. International Journal of Epidemiology , 45(6), 1887–1894. doi: 10.1093/ije/dyw341.
• Thoemmes, F., Rosseel, Y., & Textor, J. (2018). Local fit evaluation of structural equation models using graphical criteria. Psychological Methods , 23(1), 27–41. doi: 10.1037/met0000147.

In this publication, author's conflict of interest and data availability statement have been added.

The current version online now includes this information and may be considered the authoritative version of record.

Number of times cited according to CrossRef: 40

• Leire Luque-García, Gonzalo García-Baquero, Aitana Lertxundi, Wael K. Al-Delaimy, Jordi Julvez, Marisa Estarlich, Montserrat De Castro, Mònica Guxens, Manuel Lozano, Mikel Subiza-Pérez, Jesús Ibarluzea, Exploring the pathways linking prenatal and early childhood greenness exposure to attention-deficit/hyperactivity disorder symptoms during childhood: An approach based on robust causal inference, International Journal of Hygiene and Environmental Health, 10.1016/j.ijheh.2024.114475, 263 , (114475), (2025).
• Igoche Bernard Igoche, Gabriel Terna Ayem, The Role of Big Data in Sustainable Solutions, Designing Sustainable Internet of Things Solutions for Smart Industries, 10.4018/979-8-3693-5498-8.ch007, (169-208), (2024).
• Ratna Juwita, Patronella Mateha, Moving toward a Healthy Eating Pattern: Exploring the Interrelationship of Knowledge, Attitudes, and Behavior in Young Adults, Indonesian Journal of Education Research (IJoER), 10.37251/ijoer.v5i2.936, 5 , 2, (69-75), (2024).
• Christian B. H. Thorjussen, Kristian Hovde Liland, Ingrid Måge, Lars Erik Solberg, Computational Test for Conditional Independence, Algorithms, 10.3390/a17080323, 17 , 8, (323), (2024).
• Javier Mancilla-Galindo, Jesus Elias Ortiz-Gomez, Orlando Rubén Pérez-Nieto, Audrey De Jong, Diego Escarramán-Martínez, Ashuin Kammar-García, Luis Carlos Ramírez Mata, Adriana Mendez Díaz, Manuel Alberto Guerrero-Gutiérrez, Preoperative Atelectasis in Patients with Obesity Undergoing Bariatric Surgery: A Cross-Sectional Study, Anesthesia & Analgesia, 10.1213/ANE.0000000000007166, (2024).
• Mikel Subiza-Pérez, Gonzalo García-Baquero, Ainhoa Bereziartua, Jesús Ibarluzea, Objective and subjective accounts of urban exposures for epidemiological research on mental health. Measurement and analysis, Journal of Epidemiology and Community Health, 10.1136/jech-2023-220669, 78 , 11, (700-704), (2024).
• Ainhoa Bereziartua, Andrés Cabrera-León, Mikel Subiza-Pérez, Gonzalo García-Baquero, Salvador Delís Gomez, Ferran Ballester, Marisa Estarlich, Antonio Merelles, Ana Esplugues, Maria Angeles Irles, Carmen Barona, Rosa Mas, Laia Font-Ribera, X Bartoll, Katherine Pérez, Laura Oliveras, Anne-Claire Binter, Antonio Daponte, Leticia García Mochon, Helena García Cortés, María del Carmen Sánchez-Cantalejo Garrido, Marina Lacasaña, Rocío Cáceres, María Rueda, Marc Saez, Aitana Lertxundi, Urban environment and health: a cross-sectional multiregional project based on population health surveys in Spain (DAS-EP project) – study protocol, BMJ Open, 10.1136/bmjopen-2023-074252, 14 , 3, (e074252), (2024).
• Bern Igoche Igoche, Olumuyiwa Matthew, Peter Bednar, Alexander Gegov, Leveraging Structural Causal Models for Bias Detection and Feature Adjustment in Machine Learning Predictions, 2024 IEEE 12th International Conference on Intelligent Systems (IS), 10.1109/IS61756.2024.10705239, (1-7), (2024).
• Shuli Chen, Scott C. Stark, Antonio Donato Nobre, Luz Adriana Cuartas, Diogo de Jesus Amore, Natalia Restrepo-Coupe, Marielle N. Smith, Rutuja Chitra-Tarak, Hongseok Ko, Bruce W. Nelson, Scott R. Saleska, Amazon forest biogeography predicts resilience and vulnerability to drought, Nature, 10.1038/s41586-024-07568-w, 631 , 8019, (111-117), (2024).
• Mikel Subiza-Pérez, Kimon Krenz, Aidan Watmuff, Tiffany Yang, Simon Gilbody, Laura Vaughan, John Wright, Rosemary R.C. McEachan, Social inequalities, residential greenness and common mental disorders in women: evidence from the Born in Bradford family cohort study, Urban Forestry & Urban Greening, 10.1016/j.ufug.2024.128241, 94 , (128241), (2024).
• Guillem Vich, Mikel Subiza-Pérez, Asier Anabitarte, Gonzalo García-Baquero, Carolina Rueda, Antoni Colom, Carme Miralles-Guasch, Aitana Lertxundi, Jesús Ibarluzea, Xavier Delclòs-Alió, Visiting natural open spaces in urban areas during pregnancy and its association with daily physical activity, Health & Place, 10.1016/j.healthplace.2024.103297, 89 , (103297), (2024).
• Anna K. Porter, Sarah E. Kleinschmidt, Kara L. Andres, Courtney N. Reusch, Ryan M. Krisko, Oyebode A. Taiwo, Geary W. Olsen, Matthew P. Longnecker, Occurrence of COVID-19 and serum per- and polyfluoroalkyl substances: A case-control study among workers with a wide range of exposures, Global Epidemiology, 10.1016/j.gloepi.2024.100137, 7 , (100137), (2024).
• Eva Maire, James P.W. Robinson, Matthew McLean, Suchinta Arif, Jessica Zamborain-Mason, Joshua E. Cinner, Sebastian C.A. Ferse, Nicholas A.J. Graham, Andrew S. Hoey, M. Aaron MacNeil, David Mouillot, Christina C. Hicks, Managing nutrition-biodiversity trade-offs on coral reefs, Current Biology, 10.1016/j.cub.2024.08.031, (2024).
• Paolo Fusco, Paola Nasta, Eugenia Quiros-Roldan, Alice Tondinelli, Cecilia Costa, Chiara Fornabaio, Nicola Mazzini, Mattia Prosperi, Carlo Torti, Giampiero Carosi, Efficacy, Convenience, Safety and Durability of DTG-Based Antiretroviral Therapies: Evidence from a Prospective Study by the Italian MaSTER Cohort, Viruses, 10.3390/v15040924, 15 , 4, (924), (2023).
• Brian En Chyi Lee, Mathew Ling, Leanne Boyd, Craig A. Olsson, Jade Sheen, Key predictors of psychological distress and wellbeing in Australian frontline healthcare workers during COVID-19 (Omicron wave), Frontiers in Psychology, 10.3389/fpsyg.2023.1200839, 14 , (2023).
• A Chambers, EH Emmott, S Myers, AE Page, Emotional and informational social support from health visitors and breastfeeding outcomes in the UK, International Breastfeeding Journal, 10.1186/s13006-023-00551-7, 18 , 1, (2023).
• Jana Fehr, Marco Piccininni, Tobias Kurth, Stefan Konigorski, Assessing the transportability of clinical prediction models for cognitive impairment using causal models, BMC Medical Research Methodology, 10.1186/s12874-023-02003-6, 23 , 1, (2023).
• Eugen Schwabauer, Marco Piccininni, Erik Freitag, Martin Ebinger, Frederik Geisler, Peter Harmel, Annegret Hille, Irina Lorenz-Meyer, Ira Rohrpasser-Napierkowski, Tobias Kurth, Jessica L Rohmann, Matthias Endres, Frieder Schlunk, Joachim Weber, Matthias Wendt, Heinrich J Audebert, Effects of Mobile Stroke Unit dispatch on blood pressure management and outcomes in patients with intracerebral haematoma: Results from the Berlin_Prehospital Or Usual Care Delivery in acute Stroke (B_PROUD) controlled intervention study, European Stroke Journal, 10.1177/23969873231213156, 9 , 2, (366-375), (2023).
• James A. Smith, Nicholas DeVito, Hopin Lee, Catherine Tiplady, Roxanna E. Abhari, Christiana Kartsonaki, Estimating the effect of COVID-19 on trial design characteristics: a registered report, Royal Society Open Science, 10.1098/rsos.201543, 10 , 1, (2023).
• Abigail E Page, Milagros Ruiz, Mark Dyble, Daniel Major-Smith, Andrea B Migliano, Sarah Myers, Wealth, health and inequality in Agta foragers, Evolution, Medicine, and Public Health, 10.1093/emph/eoad015, 11 , 1, (149-162), (2023).
• Mhairi A. Gibson, Eshetu Gurmu, Regina Chua, Hannelore Van Bavel, Sarah Myers, Abandoning female genital mutilation/cutting (FGMC) is an emerging but costly parental investment strategy in rural Ethiopia, Social Science & Medicine, 10.1016/j.socscimed.2023.116170, 335 , (116170), (2023).
• Rafael Quintana, From single attitudes to belief systems: Examining the centrality of STEM attitudes using belief network analysis, International Journal of Educational Research, 10.1016/j.ijer.2023.102179, 119 , (102179), (2023).
• Mikel Subiza-Pérez, Gonzalo García-Baquero, Ana Fernández-Somoano, Mónica Guxens, Llucia González, Adonina Tardón, Payam Dadvand, Marisa Estarlich, Montserrat de Castro, Rosemary R.C. McEachan, Jesús Ibarluzea, Nerea Lertxundi, Residential green and blue spaces and working memory in children aged 6–12 years old. Results from the INMA cohort, Health & Place, 10.1016/j.healthplace.2023.103136, 84 , (103136), (2023).
• Mikel Subiza-Pérez, Gonzalo García-Baquero, Ana Fernández-Somoano, Isolina Riaño, Llucia González, Juana Maria Delgado-Saborit, Mónica Guxens, Serena Fossati, Martine Vrijheid, Amanda Fernandes, Jesús Ibarluzea, Nerea Lertxundi, Social inequalities, green and blue spaces and mental health in 6–12 years old children participating in the INMA cohort, Health & Place, 10.1016/j.healthplace.2023.103104, 83 , (103104), (2023).
• Liu Yang, Yue-Ting Deng, Yue Leng, Ya-Nan Ou, Yu-Zhu Li, Shi-Dong Chen, Xiao-Yu He, Bang-Sheng Wu, Shu-Yi Huang, Ya-Ru Zhang, Kevin Kuo, Wei Feng, Qiang Dong, Jian-Feng Feng, John Suckling, A. David Smith, Fei Li, Wei Cheng, Jin-Tai Yu, Depression, Depression Treatments, and Risk of Incident Dementia: A Prospective Cohort Study of 354,313 Participants, Biological Psychiatry, 10.1016/j.biopsych.2022.08.026, 93 , 9, (802-809), (2023).
• Gabriel Terna Ayem, Abel Ajibesin, Aamo Iorliam, Augustine Shey Nsang, A mixed framework for causal impact analysis under confounding and selection biases: a focus on Egra dataset, International Journal of Information Technology, 10.1007/s41870-023-01490-6, (2023).
• Gabriel Terna Ayem, Salu George Thandekkattu, Augustine Shey Nsang, Mathias Fonkam, Structural Causal Model Design and Causal Impact Analysis: A Case of SENSE-EGRA Dataset, Proceedings of International Conference on Communication and Computational Technologies, 10.1007/978-981-99-3485-0_4, (39-52), (2023).
• Louis Anthony Cox, Louis Anthony Cox, Toward More Practical Causal Epidemiology and Health Risk Assessment Using Causal Artificial Intelligence, AI-ML for Decision and Risk Analysis, 10.1007/978-3-031-32013-2_11, (351-379), (2023).
• George T. H. Ellison, Using Directed Acyclic Graphs (DAGs) to Represent the Data Generating Mechanisms of Disease and Healthcare Pathways: A Guide for Educators, Students, Practitioners and Researchers, Teaching Biostatistics in Medicine and Allied Health Sciences, 10.1007/978-3-031-26010-0_6, (61-101), (2023).
• Robert J. Reynolds, Ryan T. Scott, Russell T. Turner, Urszula T. Iwaniec, Mary L. Bouxsein, Lauren M. Sanders, Erik L. Antonsen, Validating Causal Diagrams of Human Health Risks for Spaceflight: An Example Using Bone Data from Rodents, Biomedicines, 10.3390/biomedicines10092187, 10 , 9, (2187), (2022).
• Michael H. Schwartz, Katherine M. Steele, Andrew J. Ries, Andrew G. Georgiadis, Bruce A. MacWilliams, A model for understanding the causes and consequences of walking impairments, PLOS ONE, 10.1371/journal.pone.0270731, 17 , 12, (e0270731), (2022).
• S.B. Schaffnit, A. E. Page, R. Lynch, L. Spake, R. Sear, R. Sosis, J. Shaver, N. Alam, M.C. Towner, M. K. Shenk, The impact of market integration on arranged marriages in Matlab, Bangladesh, Evolutionary Human Sciences, 10.1017/ehs.2022.54, 5 , (2022).
• Anna K. Porter, Sarah E. Kleinschmidt, Kara L. Andres, Courtney N. Reusch, Ryan M. Krisko, Oyebode A. Taiwo, Geary W. Olsen, Matthew P. Longnecker, Antibody response to COVID-19 vaccines among workers with a wide range of exposure to per- and polyfluoroalkyl substances, Environment International, 10.1016/j.envint.2022.107537, 169 , (107537), (2022).
• John M. Humphreys, Robert B. Srygley, Douglas Lawton, Amy R. Hudson, David H. Branson, Grasshoppers exhibit asynchrony and spatial non-stationarity in response to the El Niño/Southern and Pacific Decadal Oscillations, Ecological Modelling, 10.1016/j.ecolmodel.2022.110043, 471 , (110043), (2022).
• Maximilian Julius Lautenbach, Victor Yman, Carolina Sousa Silva, Nadir Kadri, Ioanna Broumou, Sherwin Chan, Sina Angenendt, Klara Sondén, David Fernando Plaza, Anna Färnert, Christopher Sundling, Systems analysis shows a role of cytophilic antibodies in shaping innate tolerance to malaria, Cell Reports, 10.1016/j.celrep.2022.110709, 39 , 3, (110709), (2022).
• Thibaut Pressat Laffouilhère, Julien Grosjean, Jean Pinson, Stéfan J. Darmoni, Emilie Leveque, Emilie Lanoy, Jacques Bénichou, Lina F. Soualmia, Ontological Representation of Causal Relations for a Deep Understanding of Associations Between Variables in Epidemiology, Artificial Intelligence in Medicine, 10.1007/978-3-031-09342-5_5, (47-56), (2022).
• Jenny Betsabé Vázquez-Aguirre, Nicandro Cruz-Ramírez, Marcela Quiroz-Castellanos, A Model for Learning Cause-Effect Relationships in Bayesian Networks, New Perspectives on Hybrid Intelligent System Design based on Fuzzy Logic, Neural Networks and Metaheuristics, 10.1007/978-3-031-08266-5_25, (395-417), (2022).
• Stephen M. Downs, Clinical Decision-Making, Clinical Informatics Study Guide, 10.1007/978-3-030-93765-2_6, (69-88), (2022).
• Suchinta Arif, M. Aaron MacNeil, Applying the structural causal model framework for observational causal inference in ecology, Ecological Monographs, 10.1002/ecm.1554, 93 , 1, (2022).
• Jessica L. Rohmann, Marco Piccininni, Martin Ebinger, Matthias Wendt, Joachim E. Weber, Eugen Schwabauer, Frederik Geisler, Erik Freitag, Peter Harmel, Irina Lorenz‐Meyer, Ira Rohrpasser‐Napierkowski, Christian H. Nolte, Darius G. Nabavi, Ingo Schmehl, Axel Ekkernkamp, Matthias Endres, Heinrich J. Audebert, Effect of Mobile Stroke Unit Dispatch in all Patients with Acute Stroke or TIA, Annals of Neurology, 10.1002/ana.26541, 93 , 1, (50-63), (2022).