Combining Unique Planar Biaxial Testing with Full-Field Thickness and Displacement Measurement for Spatial Characterization of Soft Tissues
Daniel Pearce, Daniel Pearce, Mark Nemcek, Mark Nemcek, Colleen Witzenburg, Colleen Witzenburg
Abstract
Soft tissues rely on the incredible complexity of their microstructure for proper function. Local variations in material properties arise as tissues develop and adapt, often in response to changes in loading. A barrier to investigating the heterogeneous nature of soft tissues is the difficulty of developing experimental protocols and analysis tools that can accurately capture spatial variations in mechanical behavior. In this article, we detail protocols enabling mechanical characterizations of anisotropic, heterogeneous soft tissues or tissue analogs. We present a series of mechanical tests designed to maximize inhomogeneous strain fields and in-plane shear forces. A customized, 3D-printable gripping system reduces tissue handling and enhances shear. High-resolution imaging and laser micrometry capture full-field displacement and thickness, respectively. As the equipment necessary to conduct these protocols is commercially available, the experimental methods presented offer an accessible route toward addressing heterogeneity. © 2022 The Authors. Current Protocols published by Wiley Periodicals LLC.
Basic Protocol 1 : Unique biaxial testing of soft tissues and tissue analogs
Basic Protocol 2 : Full-field thickness measurement of soft tissues and tissue analogs
Support Protocol 1 : Creating and speckling cruciform-shaped samples for mechanical testing
Support Protocol 2 : Creating custom gripping system to minimize sample handling
INTRODUCTION
Quantifying the mechanical behavior of soft biological tissues produces valuable information that can be linked to the structural constituents of the tissue, creating a more holistic picture of how they behave and adapt to mechanical loading. Early polymer scientists demonstrated the utility of biaxial tests for mechanically characterizing thin, highly deformable materials (Rivlin, 1948; Rivlin & Saunders, 1951; Treloar, 1948). The theory and methods in these fundamental studies were further developed by biomechanists for soft tissues, which often function as highly deformable membranes in the human body (Lanir & Fung, 1974a, 1974b). Since it was popularized in the mid-20th century, implementation of biaxial testing has often relied on the assumption of homogeneous strain fields and negligible in-plane shear forces (Sacks, 2000). These assumptions are appropriate for isotropic, homogeneous materials; however, soft biological tissues typically exhibit pronounced anisotropy and heterogeneity. Additionally, shear is often a physiologically relevant loading mechanism for soft tissues due to the structure of their complex fibrous extracellular matrix (Claeson & Barocas, 2017; Gardiner & Weiss, 2001; Sacks, 1999). Thus, the inclusion of shear in mechanical tests may result in more reliable and physiologically relevant material constant approximations.
In this article, we present protocols for unique biaxial testing and full-field thickness measurement for the mechanical characterization of soft biological tissues and tissue analogs. These samples commonly undergo large, complex deformations involving both normal and shear forces and exhibit unknown regional variation in stiffness, fiber alignment, and fiber orientation. Because the objective of the novel protocols presented here is at direct odds with the goals of most traditional biaxial tests aiming to characterize isotropic, homogeneous materials (Aydin et al., 2017; Lee, Fung, Shabetai, & LeWinter, 1987; Nemavhola, 2017; Rivlin, 1948; Rivlin & Saunders, 1951; Sacks, 2000), there are key differences from traditional methods. First, our biaxial testing protocol (Basic Protocol 1) was specifically designed to include multiple asymmetric mechanical tests in order to generate inhomogeneous strain fields and high levels of in-plane shear. Next, we rely on clamps, rather than the more standard use of sutures, to secure samples to load cells and to transfer motion from the actuators to the borders of the sample itself (Billiar & Sacks, 2000b; Debes & Fung, 1995; Humphrey, Strumpf, & Yin, 1990; Lee et al., 1987; Nemavhola, 2017, 2021). Unlike sutures, clamps do not allow the sample to rotate at the boundaries, facilitating the generation of shear boundary forces. Thirdly, we do not assume a constant sample thickness, but instead obtain full-field thickness measurements via laser micrometry (Basic Protocol 2). These three sets of data—full-field displacement, enhanced boundary force information, and full-field thickness—can be combined to yield detailed spatial descriptions of mechanics. Spatially varying material properties could then be fitted to a constitutive model via a number of successful inverse techniques (Davis, Luo, Avril, Duprey, & Lu, 2015; Katia Genovese, Casaletto, Humphrey, & Lu, 2014; Kroon & Holzapfel, 2008; Seshaiyer & Humphrey, 2003; Shih et al., 2021; Witzenburg, Raghupathy, Kren, Taylor, & Barocas, 2012; Zhao, Chen, & Lu, 2009, 2011).
Technological advancement drives our ability to obtain information about the non-negligible shear forces and strains arising during the biaxial testing of anisotropic, heterogeneous materials (Billiar & Sacks, 2000; Humphrey et al., 1990; Sacks, 2000). Developments in the field of digital image correlation (DIC) now allow for quick and affordable determinations of full-field displacements (Dong & Pan, 2017; Sutton, Wolters, Peters, Ranson, & McNeill, 1983), enabling measurement of the complex strain fields imposed. Six-degrees-of-freedom (6DOF) load cells capable of measuring both normal and shear forces throughout testing are now commercially available. Imaging methods, like laser micrometry, can capture full-field thickness contours of organic samples. Furthermore, the coupling of 2D mechanical characterizations with 3D thickness contours allows for a more accurate depiction of stress distributions in the tissue, supporting the identification of possible mechanical or structural heterogeneity. In short, our protocols, which utilize commercially available and accessible equipment, work to develop a detailed description of regional mechanics in soft tissue samples exhibiting nonlinear, anisotropic, and heterogeneous mechanical behavior through the use of novel clamping, loading, and boundary force acquisition strategies.
In Basic Protocol 1, we describe how to conduct a series of biaxial tests that produce full-field displacements and normal and shear boundary forces for soft tissues or soft tissue analogs that enable mechanical characterization of the sample. Basic Protocol 2, as well as Support Protocols 1 and 2, provides useful preparatory steps that maximize the utility and quality of biaxial testing results. In particular, Basic Protocol 2 details how to measure full-field sample thickness, Support Protocol 1 describes sample cutting and speckle pattern generation for DIC, and Support Protocol 2 provides steps for attaching the sample to the tester using a custom gripping system designed to minimize sample handling.
NOTE : When handling soft tissues or biologically derived soft tissue analogs, nitrile gloves should be worn.
Basic Protocol 1: UNIQUE BIAXIAL TESTING OF SOFT TISSUES AND TISSUE ANALOGS
Basic Protocol 1 describes how to biaxially test anisotropic, heterogeneous soft tissues and soft tissue analogs. The testing sequence is intended to induce multiple heterogeneous strain states. If conducted properly, this protocol will result in arm normal and shear forces as well as full-field displacement data. If desired, the data can be fitted using an inverse method to parameterize the sample's mechanical behavior according to a constitutive model or strain-energy function selected to accurately reflect the sample's behavior under the prescribed loading conditions. Parameterizations have been achieved using neo-Hookean, Mooney-Rivlin, Fung exponential, and Holzapfel-Gasser-Ogden strain-energy functions (Davis et al., 2015; Katia Genovese et al., 2014; Kroon & Holzapfel, 2008; Raghupathy & Barocas, 2010; Raghupathy, Witzenburg, Lake, Sander, & Barocas, 2011; Seshaiyer & Humphrey, 2003; Shih et al., 2021; Witzenburg et al., 2012; Zhao et al., 2009, 2011).
Materials
-
Speckled and clamped cruciform-shaped soft tissue sample (see Support Protocols 1 and 2)
-
0.01 M phosphate-buffered saline (PBS; ∼6 L)
-
Desktop computer (referenced biaxial system requires Intel i5-8500 processor and 16 GB RAM or better)
-
Biaxial testing system, containing:
- Actuators [e.g., TestResources, E216SP Electro Dynamic Actuator; four (4)]
- Load cells: one-degree-of-freedom (1DOF) load cells [e.g., TestResources, WF12S Miniature Fatigue Resistant Submersible IP65 Load Cells; two (2)] and 6DOF load cells [e.g., ATI, Nano 17 IP68 F/T Transducers; two (2)]
- 1DOF software (e.g., TestResources, B8-16 TestBuilder and MTL32-2020)
- 6DOF software (e.g., National Instruments LabVIEW 2019)
- Control software (e.g., TestResources, B8-16 TestBuilder)
-
Camera (e.g., Imperx, PoE-C2400, 2464 × 2056 pixels, 5 megapixels, 36 fps), with lens (e.g., Computar, M3Z1228C-MP) and image capture software (e.g., Imperx, IpxPlayer)
-
Isolation table (e.g., Thorlabs PFA51504 and B4860U)
-
Watertight acrylic bath
-
Connectors [3D printed or machined; four (4); STL Files 1 to 4 are provided in Supporting Information]
-
Gripping system (see Support Protocol 2)
Prior to biaxial testing
1.At least 30 min before the desired testing time, turn on desktop computer, biaxial testing system, and camera. Confirm that isolation table, upon which the biaxial testing system is secured, is functional and ready for use.
2.Ensure that there is enough space on hard drive for data files generated during testing.
3.Place empty watertight acrylic bath in the center of the actuators (see Fig. 1A).

4.Attach load cells to their appropriate actuators (see Fig. 1B and 1C).
5.Zero the load cells.
6.While carefully monitoring the applied forces in the 1DOF and 6DOF control softwares, attach a connector to each load cell (see Fig. 1D).
7.Place speckled and clamped cruciform-shaped soft tissue sample in the gripping system and secure it to the biaxial testing system (see Support Protocol 2).
8.Slowly add 0.01 M PBS to bath.
9.Focus camera on the surface of the sample and adjust exposure so that the speckle pattern is sharp and well defined and has sufficient contrast between light and dark regions.
10.Add preload to tissue by incrementally moving the actuators outward in the control software.
11.Set position of each actuator to zero.
Conducting biaxial testing
12.Begin imaging sample surface and recording forces.
13.Apply 10 equibiaxial stretch tests to sample at a rate of 1%/s for preconditioning such that the sample achieves a state of pseudoelasticity (Table 1).
- a
Displacement ratios are given as right arm:top arm:left arm:bottom arm. A displacement ratio of 1 indicates the maximum prescribed displacement, 0 indicates no displacement, and values between 0 and 1 are a percentage of the maximum displacement (e.g., 0.67 is 67% of the maximum displacement).
14.To maximize both shear and normal strains, conduct 15 different biaxial tests in which stretch is applied to different sample arms (Table 1).
15.Conduct one final equibiaxial stretch test (Table 1).
16.Repeat steps 13 through 15 for additional imposed arm displacement levels if desired.
Following biaxial testing
17.Drain PBS from the bath.
18.Remove sample and gripping system from the tester while carefully monitoring the forces applied to the load cells in the 1DOF and 6DOF softwares.
19.Remove connectors from each load cell.
20.Remove and clean load cells.
21.Dispose of sample appropriately.
22.Sanitize laboratory surfaces and system components.
Data analysis
23.Perform data analysis as desired.
Basic Protocol 2: FULL-FIELD THICKNESS MEASUREMENT OF SOFT TISSUES AND TISSUE ANALOGS
Basic Protocol 2 describes a technique for measuring the full-field thickness of a soft tissue or soft tissue analog. It is especially useful for samples with varying thicknesses or pronounced heterogeneity. The biaxial testing protocol discussed earlier (see Basic Protocol 1) produces 2D forces and full-field displacement data. In combination with these data, the full-field thicknesses obtained from this protocol enable quantification of sample stress.
Materials
-
Cruciform-shaped soft tissue sample (see Support Protocol 1)
-
Desktop computer (referenced biaxial system requires Intel i5-8500, 16 GB RAM or better)
-
Laser micrometer (e.g., Keyence, LJ-V7080), with software for laser micrometer visualization (e.g., LJ-Navigator 2 and LJ-Observer)
-
Motorized stage (e.g., motor: Applied Motion, NEMA 23 STM23Q-2AN; ball screw and nut: McMaster-Carr, 6641K1 and 6641K21), with motor control software (e.g., Applied Motion, ST Configurator; Applied Motion, Q Programmer)
Full-thickness measurement
1.Turn on desktop computer, laser micrometer, and motorized stage 30 min prior to use.
2.Zero out laser head by scanning the empty translating stage. Adjust for tilt of the laser or stage, if necessary.
3.Set desired laser scanning frequency (e.g., 20 Hz).
4.Place cruciform-shaped soft tissue sample onto the scanning stage in the desired orientation (see Fig. 6).

5.Use motorized stage to slowly translate the sample beneath the laser micrometer's head and then scan sample.
6.Remove tissue from the stage. Mechanically test, store, or dispose of sample appropriately.
7.Power down laser and sanitize scanning stage.
Data analysis
8.Perform data analysis as desired.
Support Protocol 1: CREATING AND SPECKLING CRUCIFORM-SHAPED SAMPLES FOR MECHANICAL TESTING
Support Protocol 1 details how to prepare soft tissue and soft tissue analog samples for biaxial testing (Basic Protocol 1). By definition, planar biaxial testing relies on the application of in-plane forces only, such that a state of plane stress can be assumed. For this assumption to be valid, samples must be thin. Because soft tissues are often naturally thin slabs, sheets, or membranes (Humphrey, 2002), planar biaxial testing is a common testing modality for soft tissues and tissue analogs. In general, it is recommended that samples undergoing biaxial testing have a thickness at least one order of magnitude less than their overall length and width (Ventsel & Krauthammer, 2001). Additionally, the ex vivo and planar nature of biaxial testing generally limits its application to quantification of passive tissue properties. Cruciform-shaped samples are commonly utilized in biaxial tests and lend themselves well to clamping (Support Protocol 2). To quantify full-field deformations using DIC, texture is applied to the sample. Here, an approach utilizing an airbrush and India ink is detailed. It produces a fine, random texture that adheres to the sample surface without altering mechanics. After achieving a satisfactory sample shape and sufficient speckle pattern, the sample is ready for gripping and biaxial testing (Basic Protocol 1).
Materials
-
Soft tissue or soft tissue analog sample
-
0.01 M PBS (e.g., Sigma-Aldrich, P3813-10PAK; pH 7.4, ∼50 ml)
-
Forceps (e.g., Fine Science Tools, 11053-10)
-
Cutting board
-
Biopsy punches (e.g., Robbins Instruments, Disposable, 10 mm Diameter, RBP-100)
-
Razor blades
-
100 × 15–mm petri dishes (e.g., VWR, 25384-302)
-
Airbrush (e.g., Master Airbrush G233) filled with India ink (e.g., Speedball Super Black India Ink 3378)
-
Air supply (∼45 psi)
1.Remove soft tissue or soft tissue analog sample from storage and place in 0.01 M PBS.

2.Use forceps to move sample from PBS to the cutting board.
3.Use a biopsy punch and razor blade to trim sample into a cruciform shape.
4.Return cruciform-shaped sample to PBS to prevent dehydration prior to testing.
5.Dispose of any trimmed remnants appropriately.
6.Place sample in an empty 100 × 15–mm petri dish and speckle sample using an airbrush filled with India ink with an appropriate air supply.
7.Sanitize instruments and laboratory surfaces.
Support Protocol 2: CUSTOM GRIPPING SYSTEM TO MINIMIZE SAMPLE HANDLING
This protocol describes how a custom gripping system is used to attach a small soft tissue or soft tissue analog sample to a biaxial testing machine (Basic Protocol 1). The specialized gripping system was designed such that a sample could be secured using a stereoscope, away from the testing machine. This gripping system utilizes clamps to secure the sample, rather than sutures, rakes, or hooks, to induce in-plane shear during biaxial testing.
Materials
-
All-purpose Krazy Glue (∼2 g)
-
Cruciform-shaped soft tissue sample (see Support Protocol 1)
-
Water-resistant sandpaper (e.g., McMaster-Carr, 4660A14)
-
Custom gripping system (3D printed or machined; STL Files 1 to 4 are provided in Supporting Information), containing:
- Bottom clamps (4)
- Base (1)
- Large thumb screws (e.g., McMaster-Carr, 99607A142)
- Top clamps (4)
- Small socket head screws (e.g., McMaster-Carr, 92196A108)
- Connectors (4)
- Small thumb screws (e.g., McMaster-Carr, 91185A257)
-
Hex-key Allen wrench set
1.Prior to testing, cut small rectangular pieces of water-resistant sandpaper and glue them to bottom clamps between the threaded holes in the custom gripping system using all-purpose Krazy Glue.
2.Attach bottom clamps to the base with large thumb screws using a hex-key Allen wrench set (see Fig. 9A).

3.Place cruciform-shaped soft tissue sample on the bottom clamps and base. Take note of sample orientation.
4.Secure top clamps on the sample using small socket head screws (see Fig. 9C).
5.Place “T”-shaped ends of the bottom clamps into the connectors (see Fig. 9D).
6.Secure each bottom clamp to a connector using a small thumb screw and then slowly remove base (see Fig. 9E).
COMMENTARY
Background Information
Biaxial testing of soft, highly deformable samples was popularized in the 1940s and 1950s, coinciding with the development of polymers. Treloar described methods for generating simple, homogeneous strain fields in thin sheets of rubber (Treloar, 1948), and Rivlin & Saunders (Rivlin, 1948; Rivlin & Saunders, 1951) proposed and demonstrated energy theories for large, homogeneous deformations of incompressible materials like rubber. The overarching themes of this early biaxial testing—specifically, homogeneous deformations of highly elastic and incompressible materials—were quickly adapted for soft biological tissues. Early biaxial tests (Lanir & Fung, 1974a, 1974b) revealed hallmark characteristics of soft tissues that differentiate them from other materials, including nonlinear force-displacement relationships, pronounced hysteresis, and mechanical anisotropy. Throughout the next two decades, biaxial testing was conducted on many different soft tissues, including skin (Alexander & Cook, 1977; Meijer, Douven, & Oomens, 1999; Schneider, Davidson, & Nahum, 1984), bladders (Gloeckner, Sacks, Chancellor, & deGroat, 1999; Gloeckner et al., 2002; Nagatomi, Chancellor, & Sacks, 2003), arteries (Chuong & Fung, 1986; Chuong & Fung, 1983; Dobrin & Canfield, 1984; Fung et al., 1979), heart valves (Billiar & Sacks, 2000; Lo & Vesely, 1995; Stella & Sacks, 2007), pericardium (Chew, Yin, & Zeger, 1986; Lee, Lewinter, Freeman, Shabetai, & Fung, 1985; Lee et al., 1987), endocardium and epicardium (Humphrey et al., 1990; Kang, Humphrey, & Yin, 1996), and myocardium (Demer & Yin, 1983; Sacks & Chuong, 1993; Yin, Strumpf, Chew, & Zeger, 1987). From these studies, foundational principles integral to the biaxial testing of soft tissues arose, including preconditioning and pseudoelasticity (Fung et al., 1979; Tong & Fung, 1976), residual stresses (Chuong & Fung, 1986), and exponential strain energy functions and strain-stiffening behavior (Choi & Vito, 1990; Guccione, McCulloch, & Waldman, 1991; Tong & Fung, 1976). In addition to these more general concepts, tissue-specific practices also developed. For example, skin typically exhibits pseudoelasticity following three preconditioning cycles (Zeng et al., 2004), whereas cardiovascular samples often require 8 to 10 cycles of preconditioning (Demer & Yin, 1983; Fung et al., 1979; Weizsäcker, Lambert, & Pascale, 1983). In contrast, tendons exhibit more prominent viscoelastic behavior and are typically preconditioned using cyclic stress-relaxation tests (McGough, Debski, Taskiran, Fu, & Woo, 2013; Sverdlik & Lanir, 2002).
During biaxial testing, in-plane shear forces can arise naturally from the inherent anisotropy and heterogeneous composition of a tissue's intricate and dynamic extracellular matrix (Humphrey, Dufresne, & Schwartz, 2014). To manage this issue, biomechanists developed strategies to limit the presence of these forces, some of which include aligning a specimen's primary fiber direction along testing axes and using sutures, rather than clamps, to connect the sample to the testing machine (Jacobs, Cortes, Vresilovic, & Elliott, 2013; Jiang, Sridhar, Robbins, Freed, & Moreno, 2021; Sacks, 2000; Sun, Sacks, & Scott, 2005). Sutures allow rotation at the sample boundaries, ensuring force application perpendicular to the sample's boundary. Unfortunately, they also introduce damage to the sample and create stress concentrations around the puncture sites (Cilla, Corral, Peña, & Peña, 2020; Eilaghi, Flanagan, Brodland, & Ethier, 2009; Sun et al., 2005). A few biomechanists have created custom systems with larger numbers of actuators and load cells to actually measure in-plane shear forces (Khalsa, Hoffman, & Grigg, 1996; Malcolm, Nielsen, Hunter, & Charette, 2002). However, the increased cost and complexity of these systems have limited their broader use (Sacks, 2000). The combination of commercially available 6DOF load cells and biaxial testing machines reduces these concerns while enabling measurement of in-plane shear forces.
Much like in-plane shear forces, inhomogeneous displacement fields occur commonly in soft tissues due to existing heterogeneity and anisotropy. Because the fundamental theories presented by Rivlin, Saunders, Treloar, and other rubber experts relied on homogeneous deformation and strain fields (Jones & Treloar, 1975; Rivlin & Saunders, 1951; Treloar, 1948), a common approach for soft tissues is to consider only a small central region of the soft tissue specimen when computing deformation and strain and to assume homogeneity within that region (Deplano et al., 2016; Eilaghi et al., 2009). Strategic placement of markers on the sample surface facilitates this approach (Hoffman & Grigg, 1984; Humphrey, Vawter, & Vito, 1987; Thomopoulos, Fomovsky, & Holmes, 2005). Full-field displacement measurements can be made to evaluate and validate the location, size, and presence of a supposed homogeneous strain region (Haddadi & Belhabib, 2008; Palanca, Tozzi, & Cristofolini, 2016). The most commonly applied technique used to assess full-field strains and displacements of a material is DIC (Quino et al., 2020). DIC utilizes cross-correlation algorithms to determine matching subsets of two consecutive images obtained during mechanical testing (Chu, Peters, Ranson, & Sutton, 1982; Chu, Ranson, & Sutton, 1985; Dong & Pan, 2017; Sutton et al., 1983). This approach has undergone immense advancements driven by the development of digital cameras, affordable and accessible computing power, and efficient, automated cross-correlation algorithms. Along with these innovations, the contactless, non-destructive nature of DIC makes it particularly attractive for soft biological tissues.
The accuracy and resolution of DIC depend largely on the quality of the speckle pattern produced on a sample's surface. In general, high-quality speckle patterns are random and isotropic (Yang, Tao, & Franck, 2021), exhibit stark contrast from the sample's base coloring (Reu, 2015), are finely distributed [Reu (2014) suggests speckles that are approximately 3 to 5 pixels in size], and adhere well to the sample's surface without altering its mechanical behavior (Quino et al., 2020). Generating a robust speckle pattern on hydrated, highly deformable soft tissues is challenging, and there is no consensus on the best method. Aerosolization is one common technique used for speckling soft biological tissues (Berfield et al., 2007; Crammond, Boyd, & Dulieu-Barton, 2011; Lionello & Cristofolini, 2014; Lionello, Sirieix, & Baleani, 2014; Zhou et al., 2016). For airbrush systems, the size and distribution of speckles depend on nozzle diameter, distance between the sample and the nozzle, air pressure, and viscosity of the dye (Dong & Pan, 2017). Given the lighter color of soft tissues, dark dyes, such as India ink, Verhoeff's stain, methylene blue, or Cancer Diagnostics tissue staining dye, are common (Katia Genovese, Montes, Martínez, & Evans, 2015; Lake & Barocas, 2012; Luyckx et al., 2014; Myers, Coudrillier, Boyce, & Nguyen, 2010; Walsh et al., 2020; Witzenburg et al., 2012; Zhou et al., 2016). Conversely, if the tissue is darker in color, a lighter-colored dye may be appropriate (Barranger, Doumalin, Dupré, & Germaneau, 2010; Palanca et al., 2016). Temporary tattoo ink and water-slide paper are less common dye application methods that enable reproducible patterns (Quino et al., 2020). Dyes are suitable for large deformations because they adhere to the sample surface, but it can be challenging to produce fine patterns, and the stiffness and volume of the dye should be minimized to avoid altering mechanics (Crammond et al., 2011). Powders such as graphite powder are also commonly used to speckle biological samples (Myers et al., 2010; Wang, Xie, Li, & Zhu, 2012). When applied, they create fine patterns with little impact on mechanics but often adhere poorly to tissue surfaces. Thus, powders can be challenging to utilize when deformations are large or when samples are immersed in fluid (Palanca et al., 2016). Other novel techniques for creating high-quality speckle patterns utilize lithography (Tanaka, Yang, Liu, & Kagawa, 2007), focused ion beams (Zhu, Xie, Xue, Wang, & Li, 2015), and surface abrasion (Dong, Kakisawa, & Kagawa, 2015). For more information on recent developments in DIC and speckle pattern fabrication, reviews by Dong & Pan and Palanca et al. are recommended (Dong & Pan, 2017; Palanca et al., 2016).
Following the successful completion of the protocols described here, spatial material properties could be fitted to the full-field displacement data, boundary forces, and full-field thicknesses produced utilizing an inverse approach. A variety of inverse techniques have been implemented in direct, iterative, and pointwise manners to model soft tissue mechanics (Davis et al., 2015; Katia Genovese et al., 2014; Kroon & Holzapfel, 2008; Seshaiyer & Humphrey, 2003; Zhao et al., 2009, 2011). In the past, we have developed and applied a generalized anisotropic inverse mechanics method to estimate regional differences in stiffness and mechanical anisotropy (Raghupathy & Barocas, 2010; Raghupathy et al., 2011; Shih et al., 2021; Witzenburg et al., 2012), but the resultant data from this novel technique are of independent value, and their analysis need not be limited to our inverse method.
Load-bearing tissues rely on the incredible complexity of their microstructure for proper function. Thus, there has been a broad effort to characterize their mechanical behavior. Importantly, adaptation to local changes in loading involves regional remodeling, such that even healthy tissues often display spatial variation in mechanical behavior and properties. A barrier to investigating the heterogeneous nature of soft tissues is the lack of experimental protocols and analysis tools that can accurately capture these spatial variations in whole-tissue specimens. Fortunately, new testing techniques and technology are enabling more detailed, full-field measurements of tissue behavior, such as digital volume correlation (Luetkemeyer, Cai, Neu, & Arruda, 2018; Midgett et al., 2016) and omnidirectional DIC (Genovese, 2019). Here, we present a unique biaxial testing protocol (Basic Protocol 1) designed to generate in-plane shear forces and inhomogeneous strain fields. Our protocol leverages commercially available mechanical testing equipment—namely, electrodynamic actuators, axial and 6DOF load cells, and high-resolution imaging systems—to capture 3D, undeformed sample geometry as well as full-field deformation and axial and shear forces during a series of unique biaxial extensions.
Critical Parameters
A critical aspect of this set of protocols is sample handling, which depends largely on the type of tissue or tissue analog. TissueMend, for example, is a more robust analog than collagen gels, which require more delicate handling. Rough or notched sample edges often lead to tearing during biaxial extension (Basic Protocol 1). We suggest using biopsy punches to generate smooth curved sample edges in one motion. Custom gripping systems (Support Protocol 2), like the one presented here, can also reduce handling-related damage.
A high-quality speckle pattern is necessary for accurate quantification of displacements and strains throughout the biaxial testing protocol (Basic Protocol 1). Applying speckle patterns to soft tissues (Support Protocol 1) can be challenging, especially if the tissue must be hydrated throughout preparation and testing. Removing a speckle pattern from a soft tissue or tissue analog is often not possible, and small adjustments to air pressure, the distance from the sample, and the amount of dye or powder released can greatly affect the final speckle pattern. It is wise to fine-tune these parameters on affordable materials prior to speckling valuable or limited specimens. Estrada & Franck have developed a fast, user-friendly, open-source MATLAB code to analyze the quality of speckle patterns for several different deformation types that may be useful for quantitatively assessing pattern quality (Estrada & Franck, 2015).
We suggest careful consideration of overall tissue stiffness and physiologic loading when selecting the range and resolution of both 1DOF and 6DOF load cells. If the maximum capacity of the cell is exceeded, it may break, requiring costly replacement. However, as the maximum force capacity increases, the signal-to-noise ratio is reduced. Load cells should also be properly maintained to ensure accurate measurement of normal and in-plane shear forces. Regular calibration according to manufacturer standards is recommended. PBS is highly corrosive, and even immersible stainless steel load cells will rust if not properly cleaned between testing sessions.
Troubleshooting
Table 2 includes potential problems that may arise during the implementation of the protocols presented. This collection of problems is not comprehensive but does include issues that we have faced and overcome with moderate success.
| Problem | Possible cause | Solution |
|---|---|---|
| Damaged sample | Improper handling | Exercise more caution next time; explore alternative tissue analogs (if applicable) |
| Sample slipping during biaxial testing | Clamps not secured | Ensure clamps are fully tightened down prior to testing |
| Floating speckle during biaxial testing | Speckle pattern was not allowed to dry long enough; poor speckling material | Allow ≥10 min for speckle pattern to dry; use pipets to remove as much excess speckle as possible; experiment with other materials and techniques |
| Unrealistic thickness measurements | Laser micrometer not zeroed out properly | Calibrate laser micrometer prior to measurements; adjust in post-processing |
| Unrealistic displacement fields | Low-quality speckle pattern; floating speckle | Allow ≥10 min for speckle pattern to dry; use pipets to remove as much excess speckle as possible; computationally deform sample and confirm strain with DIC code |
| Unrealistic force signals | Improperly calibrated load cells; broken load cells | If possible, calibrate load cells in-house; otherwise, send load cells to manufacturer for evaluation, calibration, and repair |
Understanding Results
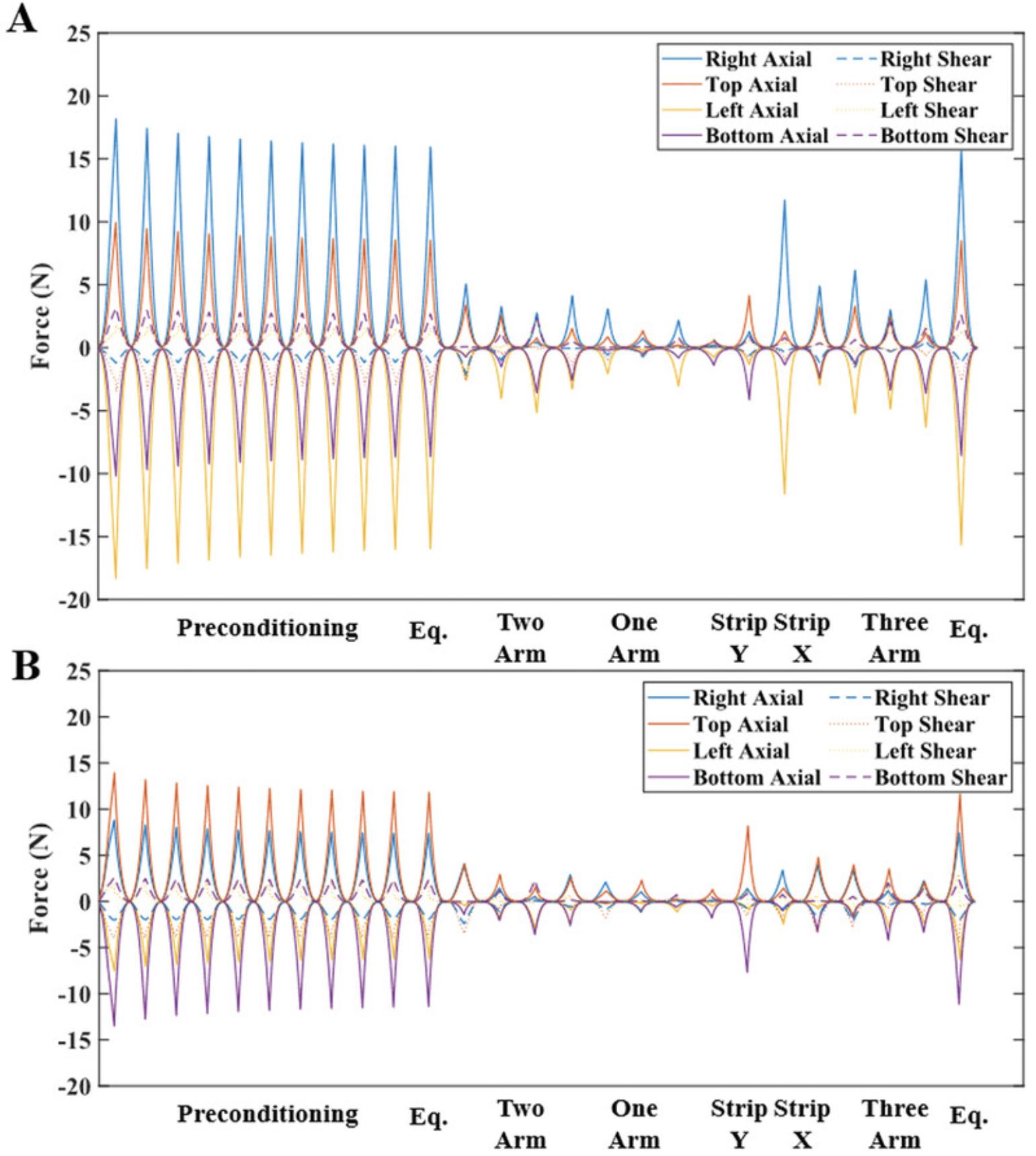
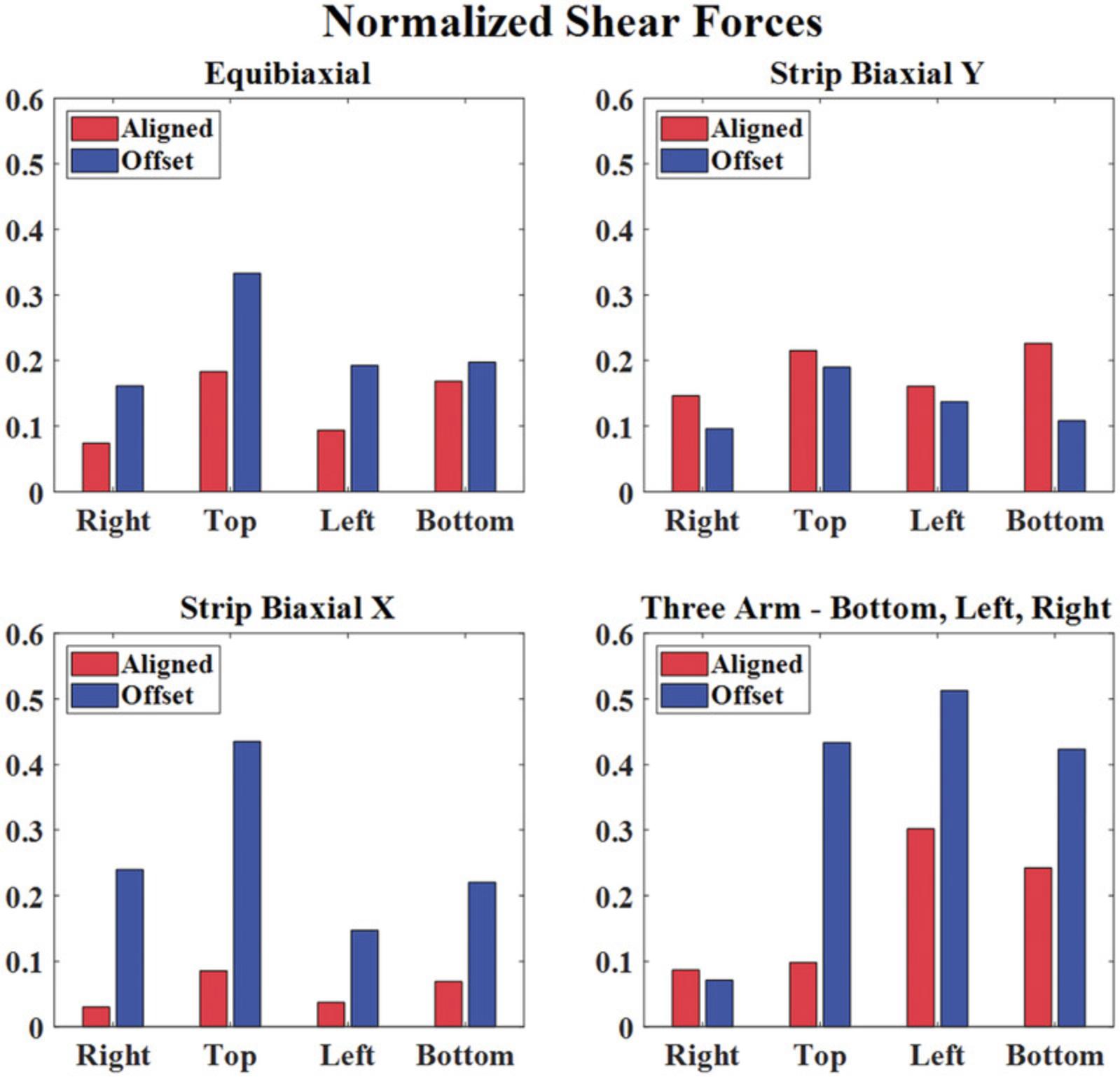
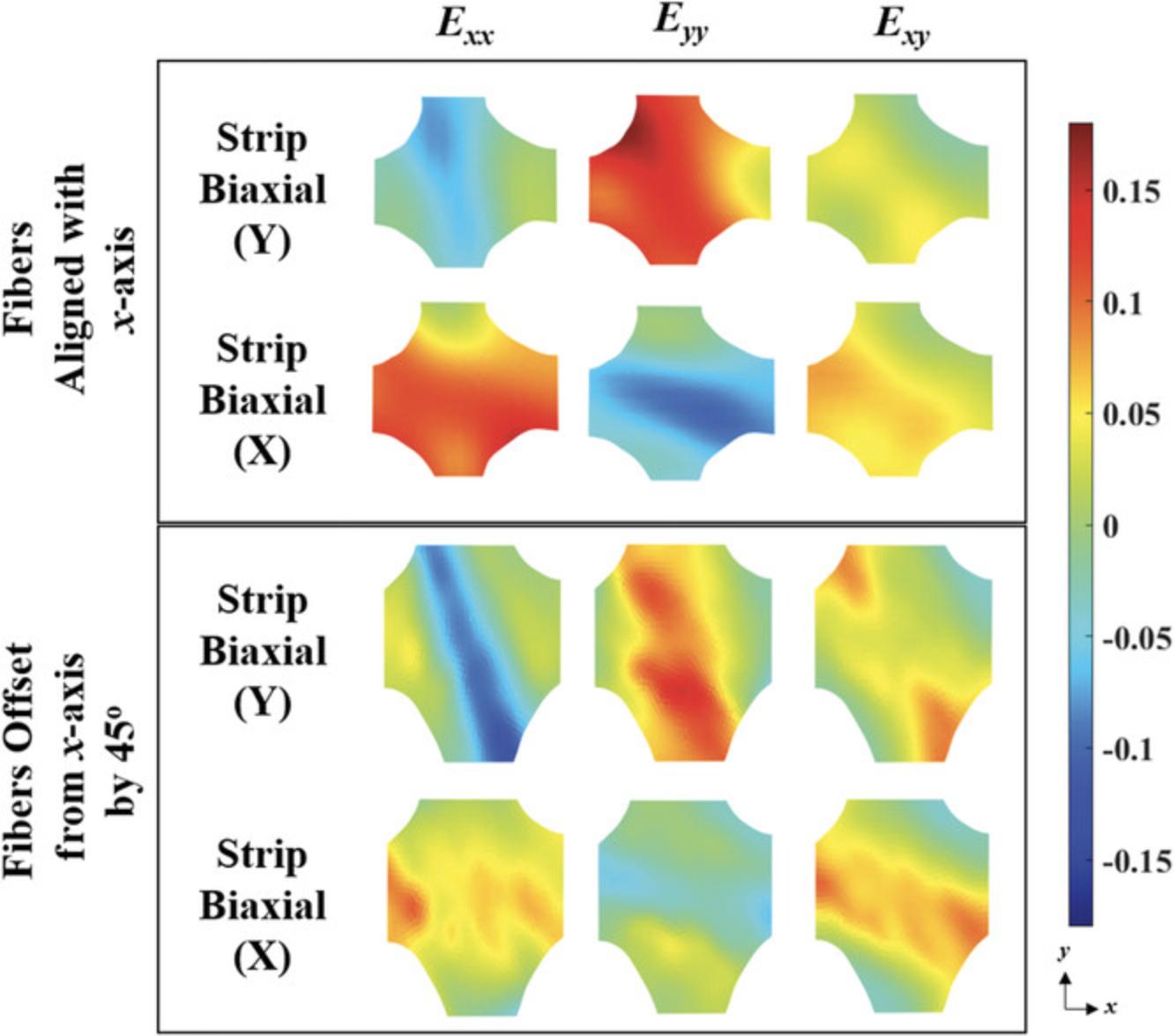
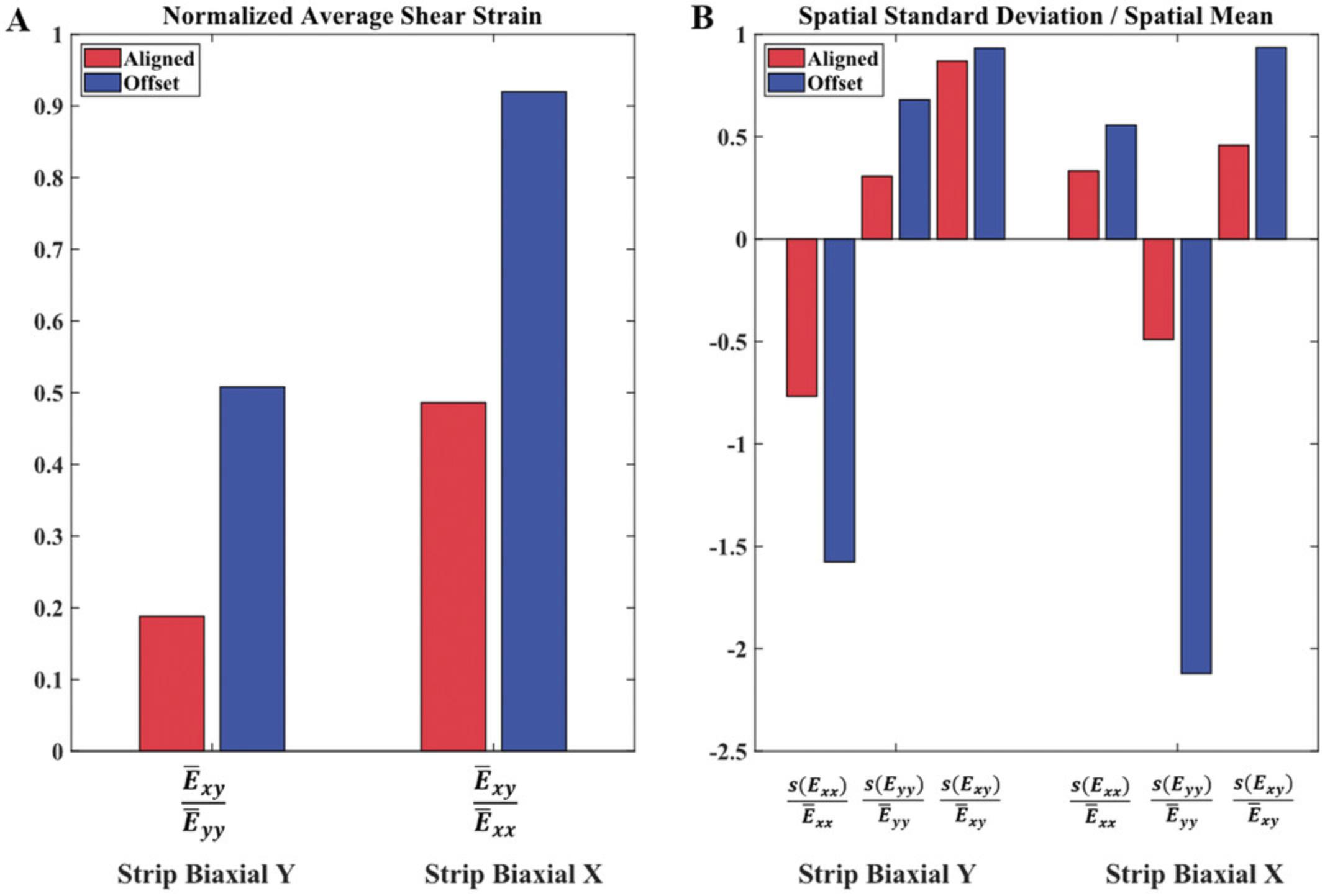
The planar biaxial testing protocol described in Basic Protocol 1 generates images of the sample surface throughout testing and normal and shear arm forces for a thin cruciform-shaped tissue or tissue analog. Figure 2 shows the measured normal and shear boundary forces for two different representative TissueMend samples: one aligned such that its stiffest axis was along the x -axis of the testing system and one such that its stiffest axis was offset by 45° from the x -axis of the testing system. To compare these samples, we plotted the shear forces along the right, top, left, and bottom arms normalized to the largest force measured during each extension (Fig. 3). For the symmetric extensions (equibiaxial and strip biaxial extensions), the aligned sample exhibited small shear forces that were <23% of the maximum normal force. Shear forces were generally larger for the offset sample for these extensions, approaching 44% of the maximum normal force in some cases. Notably, shear forces were very large for the offset sample during asymmetric extensions (>50% of the maximum normal force) and approached 30% of the maximum normal force even for the aligned sample. These results demonstrate that the use of 6DOF load cells results in robust measurement of both normal and shear forces, potentially enabling biaxial testing of samples with unknown or heterogeneous fiber alignments or anisotropy.
Using DIC software, full-field displacements and strains were computed from the images of the sample surface obtained during Basic Protocol 1. Figure 4 shows Green strain contours for the strip biaxial extensions for the two representative TissueMend samples tested and discussed in Figures 2 and 3. We computed the spatial averages and standard deviations of strain to compare the strain contours measured in the TissueMend samples quantitatively. Shear strain increased about 2-fold for the offset sample, and heterogeneity was increased in every strain component (Fig. 5). There are a number of DIC codes available for use (e.g., Blaber, Adair, & Antoniou, 2015; Solav, Moerman, Jaeger, Genovese, & Herr, 2018; Yang & Bhattacharya, 2019a, 2019b). For the strain contours shown in Figure 4, we used a code developed especially for soft tissues (Raghupathy & Barocas, 2013). It is available at https://license.umn.edu/product/robust-image-correlation-based-strain-calculator-for-tissue-systems. Prior to testing soft biological tissues, the direction of fiber alignment, stiffness, and composition of the sample are rarely known. Our biaxial testing protocol generates heterogeneous strain fields as well as elevated shear strains so that samples can be mechanically characterized regardless of their orientation or constituents.
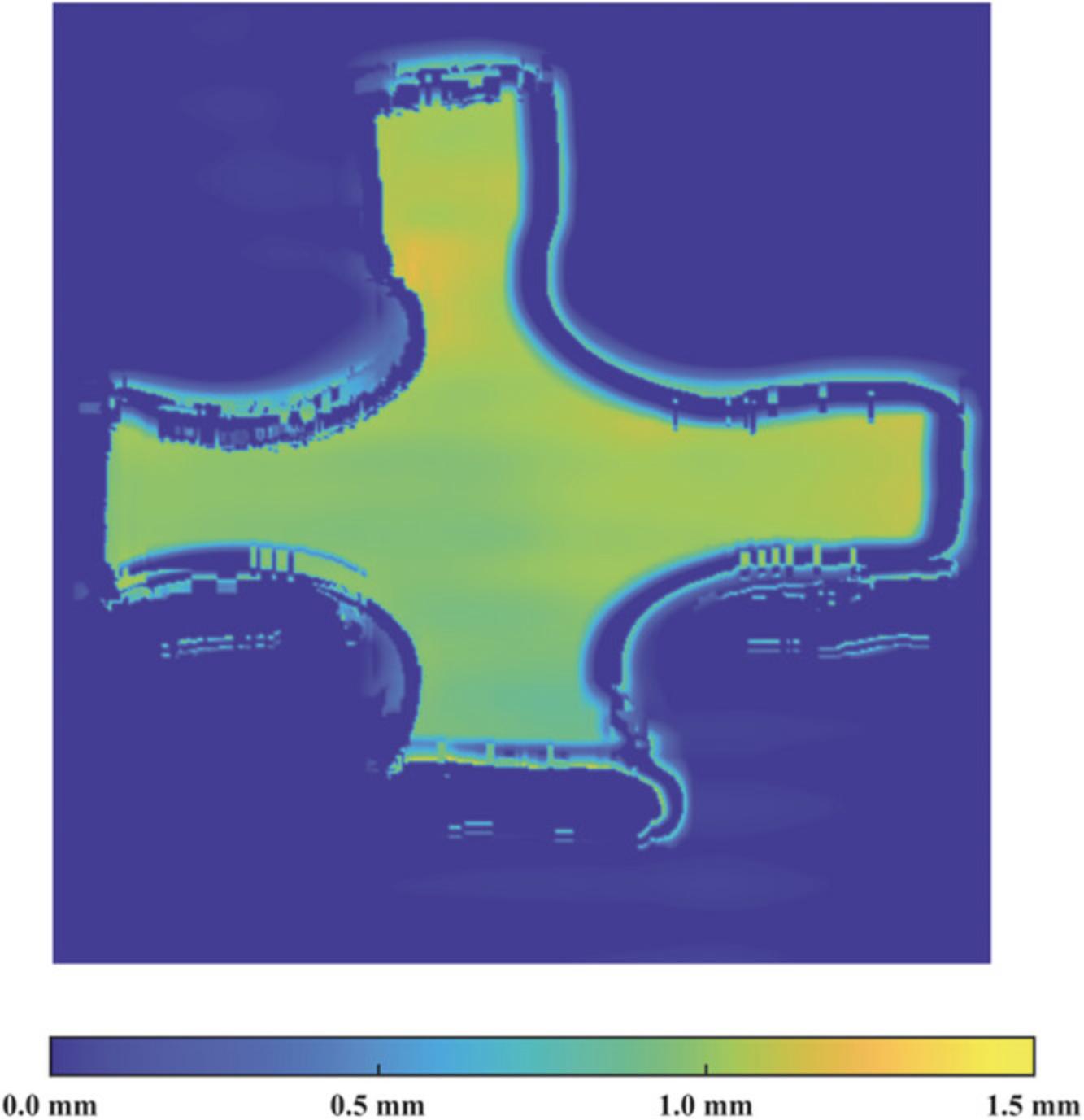
A series of thickness profiles was stored and saved by the laser during scanning, as described in Basic Protocol 2. Utilizing the motor speed, the set of profiles was converted from a function of time to a function of distance, smoothed using a Gaussian filter, and merged together to create full-field thickness contours of the scanned sample via a custom MATLAB code (Supporting Information, File 6). Figure 7 shows the full-field thickness of the TissueMend sample aligned such that its stiffest axis was along the x -axis of the testing system. Given that TissueMend is a commercially available product intended to replicate the behavior and appearance of tendons, it is likely that the homogeneous thickness is favorable.
Time Considerations
In total, these protocols require approximately 4 to 5 hr. Biaxial testing (Basic Protocol 1) requires ∼2 hr to complete, but timing will vary based on the number of testing rounds, the prescribed strain, and the strain rate. For example, one round of testing to 10% prescribed strain at 1%/s can be conducted faster than multiple rounds of testing at higher strains and lower strain rates. Rapid completion (about 2 to 3 min) of thickness measurements (Basic Protocol 2) is recommended to avoid dehydration effects. Preparing, speckling, gripping, and securing the sample into the testing machine (Support Protocols 1 and 2) can be slow, taking up to 2 hr, but are critical to the success of biaxial testing. For frozen tissue, additional time will be needed for thawing.
Acknowledgments
This work was funded by a grant from the National Science Foundation Division of Civil, Mechanical and Manufacturing Innovation (ID, 2030173) to C.M.W. The authors would also like to thank Michael Chiariello, Elizabeth Gunderson, Jiujiu Pan, Riley Pieper, and Shreya Sreedhar for their assistance on various projects that have made these protocols possible.
Author Contributions
Daniel Pearce : Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Visualization, Writing—original draft, Writing—review and editing; Mark Nemcek : Methodology, Writing—original draft, Writing—review and editing; Colleen Witzenburg : Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Visualization, Writing—original draft, Writing—review and editing.
Conflict of Interest
The authors declare no conflict of interest.
Open Research
Data Availability Statement
The data, 3D part files, and materials (product numbers and vendors) that support the protocol are available in the Supporting Information or from the corresponding author upon request.
Supporting Information
| Filename | Description |
|---|---|
| cpz1493-sup-0001-DataFile.zip34.4 MB | Supporting Information |
Please note: The publisher is not responsible for the content or functionality of any supporting information supplied by the authors. Any queries (other than missing content) should be directed to the corresponding author for the article.
Literature Cited
- Alexander, H., & Cook, T. H. (1977). Accounting for natural tension in the mechanical testing of human skin. Journal of Investigative Dermatology , 69(3), 310–314. doi: 10.1111/1523-1747.ep12507731
- Aydin, R. C., Brandstaeter, S., Braeu, F. A., Steigenberger, M., Marcus, R. P., Nikolaou, K., … Cyron, C. J. (2017). Experimental characterization of the biaxial mechanical properties of porcine gastric tissue. Journal of the Mechanical Behavior of Biomedical Materials , 74, 499–506. doi: 10.1016/j.jmbbm.2017.07.028
- Barranger, Y., Doumalin, P., Dupré, J. C., & Germaneau, A. (2010). Digital image correlation accuracy: Influence of kind of speckle and recording setup. EPJ Web of Conferences , 6, 31002. doi: 10.1051/EPJCONF/20100631002
- Berfield, T. A., Patel, J. K., Shimmin, R. G., Braun, P. V., Lambros, J., & Sottos, N. R. (2007). Micro-and nanoscale deformation measurement of surface and internal planes via digital image correlation. Experimental Mechanics , 47(1), 51–62. doi: 10.1007/S11340-006-0531-2
- Billiar, K. L., & Sacks, M. S. (2000). Biaxial mechanical properties of the natural and glutaraldehyde treated aortic valve cusp—Part I: Experimental results. Journal of Biomechanical Engineering , 122(1), 23–30. doi: 10.1115/1.429624
- Blaber, J., Adair, B., & Antoniou, A. (2015). Ncorr: Open-source 2D digital image correlation Matlab software. Experimental Mechanics , 55(6), 1105–1122. doi: 10.1007/S11340-015-0009-1/FIGURES/14
- Chew, P. H., Yin, F. C. P., & Zeger, S. L. (1986). Biaxial stress-strain properties of canine pericardium. Journal of Molecular and Cellular Cardiology , 18(6), 567–578. doi: 10.1016/S0022-2828(86)80965-8
- Choi, H. S., & Vito, R. P. (1990). Two-dimensional stress-strain relationship for canine pericardium. Journal of Biomechanical Engineering , 112(2), 153–159. doi: 10.1115/1.2891166
- Chu, T., Peters, W. H., Ranson, W. F., & Sutton, M. A. (1982). Application of digital correlation methods to rigid body mechanics. Proceedings of the Society for Experimental Stress Analysis , 73–76. doi: 10.1117/12.7973231
- Chu, T. C., Ranson, W. F., & Sutton, M. A. (1985). Applications of digital-image-correlation techniques to experimental mechanics. Experimental Mechanics , 25(3), 232–244. doi: 10.1007/BF02325092
- Chuong, C., & Fung, Y. (1986). On residual stresses in arteries. Journal of Biomechanical Engineering , 108(2), 189–192. doi: 10.1115/1.3138600
- Chuong, C. J., & Fung, Y. C. (1983). Three–dimensional stress distribution in arteries. Journal of Biomechanical Engineering , 105(3), 268–274. doi: 10.1115/1.3138417
- Cilla, M., Corral, A. V., Peña, J. A., & Peña, E. (2020). Analysis of the accuracy on computing nominal stress in a biaxial test for arteries. Strain , 56(1), e12331. doi: 10.1111/STR.12331
- Claeson, A. A., & Barocas, V. H. (2017). Planar biaxial extension of the lumbar facet capsular ligament reveals significant in-plane shear forces. Journal of the Mechanical Behavior of Biomedical Materials , 65, 127–136. doi: 10.1016/J.JMBBM.2016.08.019
- Crammond, G., Boyd, S. W., & Dulieu-Barton, J. M. (2011). Speckle pattern characterisation for high resolution digital image correlation. Applied Mechanics and Materials , 70, 261–266. doi: 10.4028/WWW.SCIENTIFIC.NET/AMM.70.261
- Davis, F., Luo, Y., Avril, S., Duprey, A., & Lu, J. (2015). Pointwise characterization of the elastic properties of planar soft tissues: Application to ascending thoracic aneurysms. Biomechanics and Modeling in Mechanobiology , 14, 967–978. doi: 10.1007/s10237-014-0646-9
- Debes, J., & Fung, Y. (1995). Biaxial mechanics of excised canine pulmonary arteries. The American Journal of Physiology , 269, H433–42. doi: 10.1152/AJPHEART.1995.269.2.H433
- Demer, L. L., & Yin, F. C. (1983). Passive biaxial mechanical properties of isolated canine myocardium. The Journal of Physiology , 339(1), 615–630. doi: 10.1113/jphysiol.1983.sp014738
- Deplano, V., Boufi, M., Boiron, O., Guivier-Curien, C., Alimi, Y., & Bertrand, E. (2016). Biaxial tensile tests of the porcine ascending aorta. Journal of Biomechanics , 49(10), 2031–2037. doi: 10.1016/J.JBIOMECH.2016.05.005
- Dobrin, P. B., & Canfield, T. R. (1984). Elastase, collagenase, and the biaxial elastic properties of dog carotid artery. The American Journal of Physiology , 247, H124–31. doi: 10.1152/Ajpheart.1984.247.1.H124
- Dong, Y., Kakisawa, H., & Kagawa, Y. (2015). Development of microscale pattern for digital image correlation up to 1400°C. Optics and Lasers in Engineering , 68, 7–15. doi: 10.1016/J.OPTLASENG.2014.12.003
- Dong, Y. L., & Pan, B. (2017). A review of speckle pattern fabrication and assessment for digital image correlation. Experimental Mechanics , 57(8), 1161–1181. doi: 10.1007/s11340-017-0283-1
- Eilaghi, A., Flanagan, J. G., Brodland, G. W., & Ethier, C. R. (2009). Strain uniformity in biaxial specimens is highly sensitive to attachment details. Journal of Biomechanical Engineering , 131(9), 091003. doi: 10.1115/1.3148467/459881
- Estrada, J. B., & Franck, C. (2015). Intuitive interface for the quantitative evaluation of speckle patterns for use in digital image and volume correlation techniques. Journal of Applied Mechanics , 82(9), 095001. doi: 10.1115/1.4030821
- Fung, Y., Fronek, K., & Patitucci, P. (1979). Pseudoelasticity of arteries and the choice of its mathematical expression. Heart and Circulatory Physiology , 6(5), H620–31. doi: 10.1152/AJPHEART.1979.237.5.H620
- Gardiner, J. C., & Weiss, J. A. (2001). Simple shear testing of parallel-fibered planar soft tissues. Journal of Biomechanical Engineering , 123(2), 170–175. doi: 10.1115/1.1351891
- Genovese, K. (2019). An omnidirectional DIC system for dynamic strain measurement on soft biological tissues and organs. Optics and Lasers in Engineering , 116, 6–18. doi: 10.1016/J.OPTLASENG.2018.12.006
- Genovese, K., Casaletto, L., Humphrey, J. D., & Lu, J. (2014). Digital image correlation-based point-wise inverse characterization of heterogeneous material properties of gallbladder in vitro. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences , 470(2167), 20140152. doi: 10.1098/rspa.2014.0152
- Genovese, K., Montes, A., Martínez, A., & Evans, S. L. (2015). Full-surface deformation measurement of anisotropic tissues under indentation. Medical Engineering and Physics , 37(5), 484–493. doi: 10.1016/j.medengphy.2015.03.005
- Gloeckner, D., Sacks, M., Chancellor, M., & De Groat, W. (1999). Active and passive biaxial mechanical properties of urinary bladder wall. Annual International Conference of the IEEE Engineering in Medicine and Biology - Proceedings , 1, 17. doi: 10.1109/IEMBS.1999.802036
- Gloeckner, D. C., Sacks, M. S., Fraser, M. O., Somogyi, G. T., De Groat, W. C., & Chancellor, M. B. (2002). Passive biaxial mechanical properties of the rat bladder wall after spinal cord injury. Journal of Urology , 167(5), 2247–2252. doi: 10.1016/S0022-5347(05)65137-3
- Guccione, J. M., McCulloch, A. D., & Waldman, L. K. (1991). Passive material properties of intact ventricular myocardium determined from a cylindrical model. Journal of Biomechanical Engineering , 113(1), 42–55. doi: 10.1115/1.2894084
- Haddadi, H., & Belhabib, S. (2008). Use of rigid-body motion for the investigation and estimation of the measurement errors related to digital image correlation technique. Optics and Lasers in Engineering , 46(2), 185–196. doi: 10.1016/J.OPTLASENG.2007.05.008
- Hoffman, A. H., & Grigg, P. (1984). A method for measuring strains in soft tissue. Journal of Biomechanics , 17(10), 795–800. doi: 10.1016/0021-9290(84)90110-6
- Humphrey, J. D., Strumpf, R. K., & Yin, F. C. P. (1990). Biaxial mechanical behavior of excised ventricular epicardium. American Journal of Physiology - Heart and Circulatory Physiology , 259, H101–8. doi: 10.1152/AJPHEART.1990.259.1.H101
- Humphrey, J. D., Vawter, D. L., & Vito, R. P. (1987). Quantification of strains in biaxially tested soft tissues. Journal of Biomechanics , 20(1), 59–65. doi: 10.1016/0021-9290(87)90267-3
- Humphrey, J. D. (2002). Cardiovascular solid mechanics. New York: Springer. doi: 10.1007/978-0-387-21576-1
- Humphrey, J. D., Dufresne, E. R., & Schwartz, M. A. (2014). Mechanotransduction and extracellular matrix homeostasis. Nature Reviews Molecular Cell Biology , 15(12), 802–812. doi: 10.1038/nrm3896
- Jacobs, N. T., Cortes, D. H., Vresilovic, E. J., & Elliott, D. M. (2013). Biaxial tension of fibrous tissue: Using finite element methods to address experimental challenges arising from boundary conditions and anisotropy. Journal of Biomechanical Engineering , 135(2), 1–10. doi: 10.1115/1.4023503
- Jiang, M., Sridhar, R. L., Robbins, A. B., Freed, A. D., & Moreno, M. R. (2021). A versatile biaxial testing platform for soft tissues. Journal of the Mechanical Behavior of Biomedical Materials , 114, 104144. doi: 10.1016/J.JMBBM.2020.104144
- Jones, D. F., & Treloar, L. R. G. (1975). The properties of rubber in pure homogeneous strain. Journal of Physics D: Applied Physics , 8(11), 1285. doi: 10.1088/0022-3727/8/11/007
- Kang, T., Humphrey, J. D., & Yin, F. C. P. (1996). Comparison of biaxial mechanical properties of excised endocardium and epicardium. American Journal of Physiology - Heart , 270, H2169–76. doi: 10.1152/ajpheart.1996.270.6.H2169
- Khalsa, P. S., Hoffman, A. H., & Grigg, P. (1996). Mechanical states encoded by stretch-sensitive neurons in feline joint capsule. Journal of Neurophysiology , 76(1), 175–187. doi: 10.1152/Jn.1996.76.1.175
- Kroon, M., & Holzapfel, G. A. (2008). Estimation of the distributions of anisotropic, elastic properties and wall stresses of saccular cerebral aneurysms by inverse analysis. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences , 464(2092), 807–825. doi: 10.1098/rspa.2007.0332
- Lake, S. P., & Barocas, V. H. (2012). Mechanics and kinematics of soft tissue under indentation are determined by the degree of initial collagen fiber alignment. Journal of the Mechanical Behavior of Biomedical Materials , 13, 25–35. doi: 10.1016/j.jmbbm.2012.03.017
- Lanir, Y., & Fung, Y. C. (1974a). Two-dimensional mechanical properties of rabbit skin—I. Experimental system. Journal of Biomechanics , 7(1), 29–34. doi: 10.1016/0021-9290(74)90067-0
- Lanir, Y., & Fung, Y. C. (1974b). Two-dimensional mechanical properties of rabbit skin—II. Experimental results. Journal of Biomechanics , 7(2), 171–182. doi: 10.1016/0021-9290(74)90058-X
- Lee, M., Lewinter, M. M., Freeman, G., Shabetai, R., & Fung, Y. C. (1985). Biaxial mechanical properties of the pericardium in normal and volume overload dogs. Heart and Circulatory Physiology , 18(2), H222–H230. doi: 10.1152/ajpheart.1985.249.2.H222
- Lee, M. C., Fung, Y. C., Shabetai, R., & Le Winter, M. M. (1987). Biaxial mechanical properties of human pericardium and canine comparisons. The American Journal of Physiology , 253, H75–82. doi: 10.1152/Ajpheart.1987.253.1.H75
- Lionello, G., & Cristofolini, L. (2014). A practical approach to optimizing the preparation of speckle patterns for digital-image correlation. Measurement Science and Technology , 25(10), 107001. doi: 10.1088/0957-0233/25/10/107001
- Lionello, G., Sirieix, C., & Baleani, M. (2014). An effective procedure to create a speckle pattern on biological soft tissue for digital image correlation measurements. Journal of the Mechanical Behavior of Biomedical Materials , 39, 1–8. doi: 10.1016/J.JMBBM.2014.07.007
- Lo, D., & Vesely, I. (1995). Biaxial strain analysis of the porcine aortic valve. The Annals of Thoracic Surgery , 60(SUPPL. 2), S374–S378. doi: 10.1016/0003-4975(95)00249-K
- Luetkemeyer, C. M., Cai, L., Neu, C. P., & Arruda, E. M. (2018). Full-volume displacement mapping of anterior cruciate ligament bundles with dualMRI. Extreme Mechanics Letters , 19, 7–14. doi: 10.1016/J.EML.2017.12.004
- Luyckx, T., Verstraete, M., De Roo, K., De Waele, W., Bellemans, J., & Victor, J. (2014). Digital image correlation as a tool for three-dimensional strain analysis in human tendon tissue. Journal of Experimental Orthopaedics , 1(1), 1–9. doi: 10.1186/s40634-014-0007-8
- Malcolm, D. T. K., Nielsen, P. M. F., Hunter, P. J., & Charette, P. G. (2002). Strain measurement in biaxially loaded inhomogeneous, anisotropic elastic membranes. Biomechanics and Modeling in Mechanobiology , 1(3), 197–210. doi: 10.1007/S10237-002-0018-8
- McGough, R. L., Debski, R. E., Taskiran, E., Fu, F. H., & Woo, S. L. Y. (2013). Mechanical properties of the long head of the biceps tendon. Knee Surgery, Sports Traumatology, Arthroscopy , 3(4), 226–229. doi: 10.1007/BF01466622
- Meijer, R., Douven, L. F. A., & Oomens, C. W. J. (1999). Characterisation of anisotropic and non-linear behaviour of human skin in vivo. Computer Methods in Biomechanics and Biomedical Engineering , 2(1), 13–27. doi: 10.1080/10255849908907975
- Midgett, D. E., Quigley, H. A., Pease, M. E., Franck, C., Toyjanova, J., Nguyen, T. D., … Toyjanova, J. (2016). Inflation test of the human optic nerve head using digital volume correlation. Conference Proceedings of the Society for Experimental Mechanics Series , 6, 7–15. doi: 10.1007/978-3-319-21455-9_2
- Myers, K. M., Coudrillier, B., Boyce, B. L., & Nguyen, T. D. (2010). The inflation response of the posterior bovine sclera. Acta Biomaterialia , 6(11), 4327–4335. doi: 10.1016/J.ACTBIO.2010.06.007
- Nagatomi, J., Chancellor, M. B., & Sacks, M. S. (2003). Active biaxial mechanical properties of bladder wall tissue. American Society of Mechanical Engineers, Bioengineering Division (Publication) BED , 55, 341–342. doi: 10.1115/IMECE2003-43146
- Nemavhola, F. (2017). Biaxial quantification of passive porcine myocardium elastic properties by region. Engineering Solid Mechanics , 5, 155–166. doi: 10.5267/j.esm.2017.6.003
- Nemavhola, F. (2021). Study of biaxial mechanical properties of the passive pig heart: Material characterisation and categorisation of regional differences. International Journal of Mechanical and Materials Engineering , 16, 1–14. doi: 10.1186/s40712-021-00128-4
- Palanca, M., Tozzi, G., & Cristofolini, L. (2016). The use of digital image correlation in the biomechanical area: A review. International Biomechanics , 3(1), 1–21. doi: 10.1080/23335432.2015.1117395
- Quino, G., Chen, Y., Ramakrishnan, K. R., Martínez-Hergueta, F., Zumpano, G., Pellegrino, A., & Petrinic, N. (2020). Speckle patterns for DIC in challenging scenarios: Rapid application and impact endurance. Measurement Science and Technology , 32(1), 015203. doi: 10.1088/1361-6501/ABAAE8
- Raghupathy, R., & Barocas, V. H. (2010). Generalized anisotropic inverse mechanics for soft tissues. Journal of Biomechanical Engineering , 132(8), 081006. doi: 10.1115/1.4001257
- Raghupathy, R., & Barocas, V. H. (2013). Robust Image Correlation Based Strain Calculator for Tissue Systems (20130022, Dr. Victor Barocas). Retrieved from https://license.umn.edu/product/robust-image-correlation-based-strain-calculator-for-tissue-systems
- Raghupathy, R., Witzenburg, C., Lake, S. P., Sander, E. A., & Barocas, V. H. (2011). Identification of regional mechanical anisotropy in soft tissue analogs. Journal of Biomechanical Engineering , 133(9), 091011. doi: 10.1115/1.4005170
- Reu, P. (2014). All about speckles: Speckle size measurement. Experimental Techniques , 38(6), 1–2. doi: 10.1111/ext.12110
- Reu, P. (2015). All about speckles: Contrast. Experimental Techniques , 39(1), 1–2. doi: 10.1111/EXT.12126
- Rivlin, R. S. (1948). Large elastic deformations of isotropic materials IV. further developments of the general theory. Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences , 241(835), 379–397. doi: 10.1098/RSTA.1948.0024
- Rivlin, R. S., & Saunders, D. W. (1951). Large elastic deformations of isotropic materials VII. Experiments on the deformation of rubber. Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences , 243(865), 251–288. doi: 10.1098/rsta.1951.0004
- Sacks, M. S. (1999). A method for planar biaxial mechanical testing that includes in-plane shear. Journal of Biomechanical Engineering , 121(5), 551–555. doi: 10.1115/1.2835086
- Sacks, M. S., & Chuong, C. J. (1993). Biaxial mechanical properties of passive right ventricular free wall myocardium. Journal of Biomechanical Engineering , 115(2), 202–205. doi: 10.1115/1.2894122
- Sacks, M. S. (2000). Biaxial mechanical evaluation of planar biological materials. Journal of Elasticity and the Physical Science of Solids , 61(1), 199–246. doi: 10.1023/A:1010917028671
- Schneider, D. C., Davidson, T. M., & Nahum, A. M. (1984). In vitro biaxial stress-strain response of human skin. Archives of Otolaryngology , 110(5), 329–333. doi: 10.1001/archotol.1984.00800310053012
- Seshaiyer, P., & Humphrey, J. D. (2003). A sub-domain inverse finite element characterization of hyperelastic membranes including soft tissues. Journal of Biomechanical Engineering , 125(3), 363–371. doi: 10.1115/1.1574333
- Shih, E. D., Provenzano, P. P., Witzenburg, C. M., Barocas, V. H., Grande, A. W., & Alford, P. W. (2021). Characterizing tissue remodeling and mechanical heterogeneity in cerebral aneursysms. Journal of Vascular Research , 59, 34–42. doi: 10.1159/000519694
- Solav, D., Moerman, K. M., Jaeger, A. M., Genovese, K., & Herr, H. M. (2018). MultiDIC: An open-source toolbox for multi-view 3D digital image correlation. IEEE Access , 6, 30520–30535. doi: 10.1109/ACCESS.2018.2843725
- Stella, J. A., & Sacks, M. S. (2007). On the biaxial mechanical properties of the layers of the aortic valve leaflet. Journal of Biomechanical Engineering , 129(5), 757–766. doi: 10.1115/1.2768111
- Sun, W., Sacks, M. S., & Scott, M. J. (2005). Effects of boundary conditions on the estimation of the planar biaxial mechanical properties of soft tissues. Journal of Biomechanical Engineering , 127(4), 709–715. doi: 10.1115/1.1933931
- Sutton, M., Wolters, W., Peters, W., Ranson, W., & McNeill, S. (1983). Determination of displacements using an improved digital correlation method. Image and Vision Computing , 1(3), 133–139. doi: 10.1016/0262-8856(83)90064-1
- Sverdlik, A., & Lanir, Y. (2002). Time-dependent mechanical behavior of sheep digital tendons, including the effects of preconditioning. Journal of Biomechanical Engineering , 124(1), 78–84. doi: 10.1115/1.1427699
- Tanaka, Y., Yang, J. M., Liu, Y. F., & Kagawa, Y. (2007). Characterization of nanoscale deformation in a discontinuously reinforced titanium composite using AFM and nanolithography. Scripta Materialia , 56(3), 209–212. doi: 10.1016/J.SCRIPTAMAT.2006.10.015
- Thomopoulos, S., Fomovsky, G. M., & Holmes, J. W. (2005). The development of structural and mechanical anisotropy in fibroblast populated collagen gels. Journal of Biomechanical Engineering , 127(5), 742–750. doi: 10.1115/1.1992525
- Tong, P., & Fung, Y. C. (1976). The stress-strain relationship for the skin. Journal of Biomechanics , 9(10), 649–657. doi: 10.1016/0021-9290(76)90107-X
- Treloar, L. R. G. (1948). Stresses and Birefringence in Rubber subjected to General Homogeneous Strain. Proceedings of the Physical Society (1926-1948) , 60(2), 135. doi: 10.1088/0959-5309/60/2/303
- Ventsel, E., & Krauthammer, T. (2001). Thin plates and shells. In Thin plates and shells. CRC Press. doi: 10.1201/9780203908723
- Walsh, D. R., Lynch, J. J., Connor, O’. D. T., Newport, D. T., & Mulvihill, J. J. E. (2020). Mechanical and structural characterisation of the dural venous sinuses. Scientific Reports , 10(1), 21763. doi: 10.1038/s41598-020-78694-4
- Wang, H., Xie, H., Li, Y., & Zhu, J. (2012). Fabrication of micro-scale speckle pattern and its applications for deformation measurement. Measurement Science and Technology , 23(3), 035402. doi: 10.1088/0957-0233/23/3/035402
- Weizsäcker, H. W., Lambert, H., & Pascale, K. (1983). Analysis of the passive mechanical properties of rat carotid arteries. Journal of Biomechanics , 16(9), 703–715. doi: 10.1016/0021-9290(83)90080-5
- Witzenburg, C., Raghupathy, R., Kren, S. M., Taylor, D. A., & Barocas, V. H. (2012). Mechanical changes in the rat right ventricle with decellularization. Journal of Biomechanics , 45(5), 842–849. doi: 10.1016/j.jbiomech.2011.11.025
- Yang, J., & Bhattacharya, K. (2019a). Augmented Lagrangian digital image correlation. Experimental Mechanics , 59(2), 187–205. doi: 10.1007/s11340-018-00457-0
- Yang, J., & Bhattacharya, K. (2019b). Fast adaptive global digital image correlation. Conference Proceedings of the Society for Experimental Mechanics Series , 12, 69–73. doi: 10.1007/978-3-319-97481-1_7
- Yang, J., Tao, J. L., & Franck, C. (2021). Smart digital image correlation patterns via 3D printing. Experimental Mechanics , 61(7), 1181–1191. doi: 10.1007/S11340-021-00720-X/TABLES/3
- Yin, F., Strumpf, R., Chew, P., & Zeger, S. (1987). Quantification of the mechanical properties of noncontracting canine myocardium under simultaneous biaxial loading. Journal of Biomechanics , 20(6), 577–589. doi: 10.1016/0021-9290(87)90279-X
- Zeng, Y. J., Liu, Y. H., Xu, C. Q., Xu, X. H., Xu, H., & Sun, G. C. (2004). Biomechanical properties of skin in vitro for different expansion methods. Clinical Biomechanics , 19(8), 853–857. doi: 10.1016/J.CLINBIOMECH.2004.05.009
- Zhao, X., Chen, X., & Lu, J. (2009). Pointwise identification of elastic properties in nonlinear hyperelastic membranes-part II: Experimental validation. Journal of Applied Mechanics, Transactions ASME , 76(6), 1–8. doi: 10.1115/1.3130810/469751
- Zhao, X., Raghavan, M. L., & Lu, J. (2011). Identifying heterogeneous anisotropic properties in cerebral aneurysms: A pointwise approach. Biomechanics and Modeling in Mechanobiology , 10(2), 177. doi: 10.1007/S10237-010-0225-7
- Zhou, B., Ravindran, S., Ferdous, J., Kidane, A., Sutton, M. A., & Shazly, T. (2016). Using digital image correlation to characterize local strains on vascular tissue specimens. Journal of Visualized Experiments , 2016(107), 53625. doi: 10.3791/53625
- Zhu, R., Xie, H., Xue, Y., Wang, L., & Li, Y. (2015). Fabrication of speckle patterns by focused ion beam deposition and its application to micro-scale residual stress measurement. Measurement Science and Technology , 26(9), 095601. doi: 10.1088/0957-0233/26/9/095601
Citing Literature
Number of times cited according to CrossRef: 8
- Alexey Liogky, Victoria Salamatova, Data-Driven Anisotropic Biomembrane Simulation Based on the Laplace Stretch, Computation, 10.3390/computation12030039, 12 , 3, (39), (2024).
- Talyah M. Nelson, Crystal A. Mariano, Gustavo O. Ramirez, Arif Badrou, Kathrine A. M. Quiros, Matthew Shankel, Mona Eskandari, Lung Mechanics: Material Characterization of Pulmonary Constituents for an Experimentally Informed Computational Pipeline, Current Protocols, 10.1002/cpz1.70001, 4 , 9, (2024).
- Antonio Boccaccio, Luciano Lamberti, Lorenzo Santoro, Bartolomeo Trentadue, Mechanical Characterization of Soft Membranes with One-Shot Projection Moiré and Metaheuristic Optimization, Applied Sciences, 10.3390/app13137758, 13 , 13, (7758), (2023).
- Vishnuvardhana Wuppaladhodi, Songlin Yang, Hossein Pouri, Jin Zhang, Enhanced mechanical properties of silicone hydrogels coated with metallic nanoparticles by using the laser-assisted process, Journal of Applied Physics, 10.1063/5.0139752, 133 , 16, (2023).
- Ali Esmaeili, Deepak George, Ian Masters, Mokarram Hossain, Biaxial experimental characterizations of soft polymers: A review, Polymer Testing, 10.1016/j.polymertesting.2023.108246, 128 , (108246), (2023).
- Klaas Vander Linden, Heleen Fehervary, Julie Vastmans, Nele Famaey, The influence of out-of-plane motion on the deformation measurement of planar biaxial tests on biological soft tissue, Mechanics Research Communications, 10.1016/j.mechrescom.2023.104099, 129 , (104099), (2023).
- Daniel P. Pearce, Mark T. Nemcek, Colleen M. Witzenburg, Don’t go breakin’ my heart: cardioprotective alterations to the mechanical and structural properties of reperfused myocardium during post-infarction inflammation, Biophysical Reviews, 10.1007/s12551-023-01068-3, 15 , 3, (329-353), (2023).
- Chien-Yu Lin, Mrudang Mathur, Marcin Malinowski, Tomasz A. Timek, Manuel K. Rausch, The impact of thickness heterogeneity on soft tissue biomechanics: a novel measurement technique and a demonstration on heart valve tissue, Biomechanics and Modeling in Mechanobiology, 10.1007/s10237-022-01640-y, 22 , 5, (1487-1498), (2022).