Analytical Ultracentrifugation (AUC): An Overview of the Application of Fluorescence and Absorbance AUC to the Study of Biological Macromolecules
Garrett B. Edwards, Garrett B. Edwards, Uma M. Muthurajan, Uma M. Muthurajan, Samuel Bowerman, Samuel Bowerman, Karolin Luger, Karolin Luger
Abstract
The biochemical and biophysical investigation of proteins, nucleic acids, and the assemblies that they form yields essential information to understand complex systems. Analytical ultracentrifugation (AUC) represents a broadly applicable and information-rich method for investigating macromolecular characteristics such as size, shape, stoichiometry, and binding properties, all in the true solution-state environment that is lacking in most orthogonal methods. Despite this, AUC remains underutilized relative to its capabilities and potential in the fields of biochemistry and molecular biology. Although there has been a rapid development of computing power and AUC analysis tools in this millennium, fewer advancements have occurred in development of new applications of the technique, leaving these powerful instruments underappreciated and underused in many research institutes. With AUC previously limited to absorbance and Rayleigh interference optics, the addition of fluorescence detection systems has greatly enhanced the applicability of AUC to macromolecular systems that are traditionally difficult to characterize. This overview provides a resource for novices, highlighting the potential of AUC and encouraging its use in their research, as well as for current users, who may benefit from our experience. We discuss the strengths of fluorescence-detected AUC and demonstrate the power of even simple AUC experiments to answer practical and fundamental questions about biophysical properties of macromolecular assemblies. We address the development and utility of AUC, explore experimental design considerations, present case studies investigating properties of biological macromolecules that are of common interest to researchers, and review popular analysis approaches. © 2020 The Authors.
INTRODUCTION
Significant advances have been made in the capabilities of analytical ultracentrifugation (AUC) in the last two decades through the development of new optical systems and analysis methods. Nevertheless, this technique, which has historically been the “gold standard” for the characterization of biological macromolecules and complexes in solution, is generally not very well understood or commonly utilized in the fields of biochemistry and molecular biology. As a result, many recent applications of AUC fall short of taking full advantage of its potential. This may be in part because literature resources on the abilities and practical use of AUC in true biological contexts are scarce. Although very good resources are available concerning the theory of AUC and approaches to data analysis, practical examples of experimental design and troubleshooting, as well as which biological questions AUC can reasonably and optimally be used to answer and how to go about answering them, remain obscure (Demeler, Brookes, Wang, Schirf, & Kim, 2010; Schuck, 2013). Resources for the latest methods focus mainly on theory and simulated data, with few direct connections to general experimental approaches (see Current Protocols article; Demeler, 2010; Demeler & Gorbet, 2016; Schuck, 2010; Zhao, Casillas, Shroff, Patterson, & Schuck, 2013). As such, the “activation energy” for utilizing this instrument is relatively high. This overview seeks to clarify the capabilities of AUC relative to other common biophysical techniques, provide a resource to serve as a starting point for researchers to apply AUC to study macromolecular interactions, and emphasize the importance of fluorescence detection systems (FDSs) for maximization and continued expansion of AUC capabilities in studying biological systems.
AUC is well suited for analysis of biological macromolecules and their interactions because a single experiment provides information on a wider range of sample properties with equal or better resolution relative to other common approaches (see comparison of approaches in Table 1) (Cole, Lary, Moody, & Laue, 2008). Unlike many other techniques used to study biological molecules in vitro, AUC is a true solution-state method, allowing the solution behavior of isolated or interacting systems to be measured in as close to a native environment as possible. In contrast to many other biophysical techniques, macromolecular properties can be probed without the need for standards, assumptions, or physical matrices that interfere with the solution behavior of particles. The range of molecular sizes to which sedimentation velocity (SV)-AUC can be applied extends from single kilodaltons to gigadalton structures (Table 1) (Maeshima et al., 2016). The lower size limit is constrained only by the maximum rotor speeds attainable by current instruments, meaning that rather small particles are theoretically within the reach of SV-AUC. Through combination of the three optical systems currently available (UV absorbance, fluorescence detection, and interference), the dynamic range of SV-AUC is also significantly greater than that of other modern solution-state biophysical techniques, such as SAXS or SANS, extending from picomolar to millimolar concentrations of biological molecules (Harding & Rowe, 2010; Rowe, 2011; Zhao, Mayer, & Schuck, 2014). In an AUC experiment, information on many samples can be collected in parallel. Using commercially available centerpieces, as many as 14 samples can be analyzed concurrently, with room for increasing that number. Sample volume requirements are relatively low, ranging from 80 to 400 µl using standard 3- or 12-mm centerpieces, without any loss of sedimentation column length. Further, the method is non-destructive, and samples can, in most cases, be resuspended after centrifugation, with no negative impact on solution contents, enabling further utilization and analysis of the samples. Analysis of AUC data can be performed with or without the application of modeling-based approaches in order to extract particle properties. Perhaps most importantly, SV-AUC experiments directly yield information on the size, diffusion, and gross shape of particles in a sample; allow quantitation of intermolecular interactions; and provide a measure of the heterogeneity and relative concentrations of particles within a sample, all from a single, properly designed experiment. This is in contrast with other approaches (Table 1) that achieve only one or a few of these properties from direct measurement.
| Methoda | Applicable size range | Solution-state? | Properties directly measured | Analysis approach | Sample reusability |
|---|---|---|---|---|---|
| SV-AUC | Kilodalton-gigadalton | Yes | Sedimentation, diffusion, intermolecular interactions, relative concentrations of sample components | Model-based and model-independent analysis of size and shape distributions | Yes |
| EMSA | Dalton-megadalton | No | Gel matrix migration as a function of charge, intermolecular interactions, relative concentrations of components that enter gel | Measurement of migration | No |
| SEC-MALS | Kilodalton-megadalton | No | Gel matrix migration as a function of size, intermolecular interactions, hydrodynamic radius, relative concentrations of sample components that flow through column | Application of standards, assumption of globularity | Yes (diluted fractions) |
| NMR | Dalton-kilodalton | Yes | Nuclear magnetic resonance, intermolecular interactions | Chemical shift comparison | Yes |
| SAXS, SANS | ∼1-1000 nanometers | Yes | Weight-averaged scattering of X-rays or neutrons | Weight-averaged model-independent analysis, single- and ensemble-structure fitting | Yes |
| DLS | Nanometer-micrometer | Yes | Weight-averaged scattering of light | Weight-averaged model-independent analysis | Yes |
| X-ray diffraction | ∼1-200 angstroms | No | Diffraction of X-rays | Electron density mapping | No |
| Electron microscopy | Angstrom-millimeter | No | Interaction with electrons | Electron density mapping | No |
- a EMSA, electrophoretic mobility shift assay; DLS, dynamic light scattering.
Ole Lamm's 1929 description of sedimentation and diffusion of particles in a sector-shaped cell, or the Lamm equation, forms the basis for SV analysis: 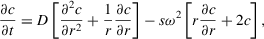
in which D is the diffusion coefficient, s is the sedimentation coefficient, r is the radial position, and c is the particle concentration along the radius of the cell at any given time t (Lamm, 1929). The relationship between solvent and physical properties of sedimenting particles is defined by the Svedberg equation: 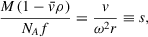
in which s is the sedimentation coefficient, v is the solute velocity, r is the radial distance from the axis of rotation, ω is the angular (rotor) velocity, M is the molecular weight, NA is Avogadro's number, f is the frictional coefficient,
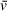
is the partial specific volume of the solute, and ρ is the density of the solvent.
From the equations above, one can conclude that SV-AUC experiments face some of the same limiting factors as other techniques that rely on separation of particles as a function of size: very similar molecules are difficult or impossible to distinguish. SV-AUC, however, is particularly well suited to examine systems containing heterogeneity of any type through fluorescence detection. The development of an FDS for Beckman XL-A/XL-I AUCs in the 2000s dramatically increased the applicability of AUC to biological macromolecular systems (MacGregor, Anderson, & Laue, 2004). To date, no other technique enables users to isolate the signal from a single species in heterogeneous solution and acquire information on the size, gross shape, and binding behavior of particles of interest in a single experiment. In addition, the higher sensitivity of fluorescence optics compared to absorbance extends the lower detection limit for data collection from protein samples from the low micromolar (µM; absorbance or interference) to the high picomolar (pM; fluorescence) or, in some cases, potentially even beyond (MacGregor et al., 2004; Zhao et al., 2014). Following the release of the FDS, significant work was done by the developers of analysis software to understand fluorescence signal artifacts and implement corrections into analysis approaches. Programs such as UltraScan and SEDFIT (Table 2) allow for processing of fluorescence data as efficiently as absorbance and interference data (Zhao et al., 2013). The increased usage and ease of fluorescent tagging of proteins and DNA in recent years and the development of ultrabright fluorophores further enable the general use of FDSs. Despite these advances, AUC-FDS has not gained widespread use. Our lab has successfully utilized this approach in the context of histone chaperones and chromatin-interacting proteins (Chassé et al., 2017; Gaullier et al., 2019; Wang et al., 2018).
| Software | Primary approach | Lamm equation solutions | Other features |
|---|---|---|---|
| DCDT+ | Time derivative (dc/dt) | Model-independent | No false-positive peaks, error estimates for all fitted parameters |
| SVEDBERG | User-selected non-interacting species models | Approximate | Fast fit convergence, error estimates for all fitted parameters, streamlined user interface |
| SEDANAL | User-selected discrete and interacting species models | Numerical | DCDT (time derivative) analysis, wide distribution analysis, BIOSPIN SE analysis |
| SEDFIT | Continuous c(s) (discrete and reacting species) | Numerical | Monte Carlo optimization, SE and ITC analysis, SEDPHAT extension for global analysis, partial specific volume calculator |
| UltraScan III | 2DSA (discrete and reacting species) | Numerical | Time derivative analysis, vHW analysis, Monte Carlo and genetic algorithm optimization, supercomputing resources, global analysis, solution density calculators |
Because Aviv Biomedical, Inc., has ceased production of the FDS for Beckman XL-A/XL-I systems, there is, as of now, no fluorescence option for SV-AUC on the market. Although the current Beckman offering, the Optima AUC, boasts advancements in data collection and resolution relative to the XL-A/XL-I systems, the fluorescence optics are still under development. Our hope is that emphasizing the strength of fluorescence-detected SV-AUC will help push the continued advancement of optical systems for the new generation of instruments. In the short term, collaborative efforts with labs or institutions that have XL-A or XL-I systems equipped with an Aviv FDS may be able to bridge the instrumentation gap.
Perhaps more significant than the advances in instrumentation, SV-AUC analysis methods rapidly evolved throughout the 20th century, allowing for simultaneous fitting of both sedimentation and diffusion information from experimental data (Claverie, Dreux, & Cohen, 1975; Demeler & Saber, 1998; Faxen, 1929; Holde & Weischet, 1978; Schuck, 1998; Stafford, 1992). Table 2 provides a reference for some widely used SV analysis software packages, their primary approach, and other useful features (Brown & Schuck, 2008; Philo, 1997, 2006; Scott, Harding, & Rowe, 2005; Stafford & Sherwood, 2004). However, software packages that implement numerical solutions of the Lamm equation, such as SEDFIT, UltraScan, and SEDANAL, have dominated SV analysis in recent years. The theoretical basis for SV analysis, regardless of method, has been thoroughly described elsewhere and will thus not be discussed here (Brown & Schuck, 2008; Philo, 1997, 2006; Scott et al., 2005; Stafford & Sherwood, 2004). Our discussion focuses instead on the practical application of UltraScan III and SEDFIT to experimental data. SEDFIT and UltraScan are both free to download, crucial functions can be accomplished easily by standard desktop computers, and both are backed up by many peer-reviewed publications and thorough tutorials and analysis aids, with authors and worldwide user bases that will actively respond to questions concerning their use (for SEDFIT: www.analyticalultracentrifugation.com and https://SEDFITsedphat.nibib.nih.gov; for UltraScan: https://www.UltraScan3.aucsolutions.com). We find that analysis using analogous UltraScan or SEDFIT approaches results in nearly identical descriptions of sedimenting systems.
GENERAL AND EXPERIMENTAL DESIGN CONSIDERATIONS
Although less “picky” than most other methods in many respects, some crucial factors outside of concentration ranges and experimental parameters need to be considered when planning AUC experiments. For basic analyses, solutions should be dilute enough that hydrodynamic non-ideality effects are negligible (e.g., macromolecules interact predominately with water and do not contain overlapping solvation layers relative to other solutes). For biological molecules, this generally means concentrations of ∼10 mg/ml or lower, inclusion of at least some (>10 mM) amount of salt for charge screening, and aqueous conditions. As outlined below, other important factors include temperature equilibration prior to acceleration, alignment of sample cells, removal of optically interfering species, knowledge of buffer properties, and, in some cases, inclusion of stabilizing agents, especially for systems with very low sample concentration. Calibration of the optical systems and radial positioning should be performed as described in the instrument manuals. Other resources for radial calibration and instrument maintenance are also available (LeBrun et al., 2018; Zhao et al., 2015) (https://uslims.aucsolutions.com/xlaresources.php).
Instrumentation
Currently, the only commercially available analytical ultracentrifuge is the Beckman Coulter Optima AUC, with a price range of
For this article, AUC access and knowledge of general usage (or access to help from an experienced user) is expected of the reader. Detailed references are available for new users (Balbo, Zhao, Brown, & Schuck, 2009; Rogge et al., 2013). A guide to Advanced Operating System (AOS) software navigation for the control and calibration of Aviv FDS instruments is available at https://www.youtube.com/watch?v=fIVLWmZ0nw4 (“Using the Fluorescence Detector in Sedimentation Velocity Analytical Ultracentrifugation”). In brief, this National Institute of Biomedical Imaging and Bioengineering video addresses the use of the FDS calibration cell filled with 100 nM fluorescein (or another dye, such as Alexa488) to radially calibrate the FDS, as well as focal depth scanning and use of programmable gain amplifiers (PGAs) and photomultiplier tube (PMT) voltage settings to maximize signal quality. Further information on FDS setup can be found in a related protocol (Chaturvedi, Ma, Zhao, & Schuck, 2017). This overview article will assume that instruments have been calibrated and that users have gained the basic AOS control software proficiency described by these resources.
In general, we use FDS focus depths of ∼4000 µm for standard 12-mm centerpieces and ∼6000 µm for 3-mm centerpieces (the optimal position puts the focus just below the upper cell window). The focus scan function in the AOS will select optimal focal depth, but sharp peaks should be avoided. To optimize sample signals (“Set gains;” set to ∼3500 intensity counts, as the detector maxes out at 4000), signal should first be maximized with PGAs (1 to 8) and then fine-tuned with the PMT voltage setting; this allows selection of the lowest PMT voltage available for any given sample, minimizing strain on the laser system. Although maximal signal provides the best signal-to-noise ratio, consistent results can be obtained with much lower fluorescence intensity if a sedimenting boundary can be observed. After temperature equilibration, acceleration to experimental speed (using either the AOS or the XL-A/XL-I control panel), verification of optimal focal depth, and signal optimization of gain settings, an experimental method setup using the AOS wizard can be started.
SV centerpieces vary in material, vertical thickness, and speed ratings. Although epon centerpieces will generally deform under less force than aluminum centerpieces, the compatibility of epon centerpieces with biological materials is much higher. A general chemical compatibility guide can be found at https://uslims.aucsolutions.com/compatibility.php. Development of new centerpiece materials and design is ongoing, already enabling manufacturing of centerpieces by AUC users with access to a suitable 3D printer (Desai, Krynitsky, Pohida, Zhao, & Schuck, 2016; Juul-Madsen, Zhao, Vorup-Jensen, & Schuck, 2019).
Temperature
Sedimentation coefficients (s , often expressed in the Svedberg unit S, equal to 10-13 seconds) are conventionally reported with correction to 20°C in water (S20,W); thus, if samples are stable at 20°C, most experiments are conducted at that temperature. However, modern AUCs can maintain 4° to 40°C (XL-A/XL-I) or 0° to 40°C (Optima), and the use of a range of temperatures can expand the type of questions that SV-AUC can address, as recently reported (Namitz, Tan, & Cosgrove, 2019). Regardless of temperature selection, AUC rotors should be given ample time to equilibrate to ensure uniform and consistent rotor stretching, as discussed elsewhere (see Current Protocols article; Zhao, Brautigam, Ghirlando, & Schuck, 2013). One-hour rotor equilibration is common at 20°C, and more time should be given for experiments conducted at lower temperatures.
Rotor Speed
Appropriate rotor speed and the number of scans to be collected are a function not only of the mass of the particle of interest but also of its diffusion characteristics, the time between scans for each sample, and sample heterogeneity (i.e., the partial concentration of unbound components). No simple relationship exists between particle mass and ideal rotor speed. Both UltraScan and SEDFIT have tools for simulating sedimentation data for particles of varying mass and shape, which can help identify a starting point. Experimentally, best practice involves a pilot experiment (see below), which is non-destructive to the sample (except in cases of concentration-dependent aggregation) and so can be run again at a different speed if experimental parameters must be changed. The fastest rotor speed available (dependent on rotor and centerpiece rating) will give the best resolution in the sedimentation coefficient dimension, whereas diffusion properties will be better resolved from slower sedimentation profiles. When possible, sedimentation data for samples to be thoroughly characterized should be collected in multiple experiments at different rotor speeds. Because the scan time and length of interval between scans collected will change with the number of samples, experimental settings, and optics used, there is no specific number of scans that users should attempt to collect. Rather, rotor speed should be selected with the goal of achieving the fastest sedimentation rate possible while still allowing for enough boundary spreading to capture diffusion information. We find that SV datasets with full sedimentation occurring within 40 to 80 scans are generally sufficient for obtaining high resolution in both sedimentation and diffusion properties. For macromolecules in the range of 50 kDa to 3 MDa, this roughly translates to rotor speeds ranging between 20,000 and 60,000 rpm. Particles below 50 kDa will require maximum rotor speeds and larger numbers of scans to observe full sedimentation. For the protein/protein and protein/DNA complexes described in the examples given here (see below, about 150 to 200 kDa in size, with frictional ratios from 1.5 to 2), rotor speeds of 30,000 to 45,000 rpm were used.
Optical System
Ideal choice of AUC optical systems varies with solution contents and concentration of the particle of interest. Absorbance optics have a lower limit of ∼0.1 optical density (OD) due to the low signal-to-noise ratio and generally should not be used above 1 OD at any wavelength due to the nonlinearity of absorbance signal. Interference optics measure refractive index changes and so have a similar lower sample concentration limit (∼0.1 mg/ml) but allow the use of much more highly concentrated samples than absorbance optics. For absorbance AUC, absorbing (usually UV-range) buffer components should be removed or included only at low concentrations. For biological samples, this generally means the exclusion of strong UV-absorbing species such as the common reducing agent dithiothreitol (DTT). Interference optics will observe signal for all buffer components, including salts, and therefore require the subtraction of buffer components from sedimentation profiles using reference samples. Interference optics scan faster and therefore provide improved radial resolution, but the use of absorbance optics in intensity mode enables the inclusion of more samples in an experiment (see https://www.uslims.aucsolutions.com/intensity.php). Neither requires specific tagging of the biological molecules under investigation. It should be noted that absorbance AUC of DNA and DNA-protein complexes with absorbance optics scanning at 260-nm wavelength enables much lower sample concentrations than when analyzing protein alone due to the higher UV extinction coefficients of DNA. In other cases of unique absorbance spectra, wavelengths other than 260 and 280 nm can be used to optimize signal.
Fluorescence optics greatly enhance the dynamic range of AUC by extending the low end of sample concentration into the low nanomolar in most cases, depending on labeling efficiency and fluorophore quantum yield, although minimal FDS power settings still enable the use of at least low-micromolar sample concentrations. As low as single-digit picomolar concentrations of fluorescent species have been reported to yield usable sedimentation data (Zhao et al., 2014).
UltraScan and SEDFIT analysis packages treat data from absorbance, interference, and fluorescence optics as essentially the same, although absorbance data collected in intensity mode must be converted to pseudo-absorbance data in both types of software (this conversion function is prompted during data import in UltraScan and is under “Options” → “Loading Options” and is in the Tools menu in SEDFIT). Due to the difference in signal units between optical systems, root-mean-square deviation (RMSD) values for model fits are on different scales, such that optimized fits for absorbance data are about 0.002 to 0.004, whereas similar RMSDs for fluorescence data are about 20 to 40.
Partial Specific Volume (
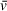
)
In an AUC experiment, accurately determining the partial specific volume, that is, the volume of solvent displaced by a particle, is a crucial component for extracting molecular weight, as seen in the Svedberg equation. It should be emphasized that SV analysis seeks to describe experimentally observed sedimentation and diffusion behavior by fitting s and f/f0 (related to the diffusion coefficient, f/f0 is the ratio of the frictional coefficient f to the frictional coefficient of a theoretical sphere of the same mass and
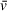
, f0). An initial estimate of
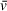
and particle mass is required to define f0 , necessitating that users guess the likely composition of the system. Although some error is tolerable here, it is important to at least define whether the solutes are predominately protein, DNA, or a mixture, and if this estimate is subsequently found to be inaccurate, the analysis should be redone with a more appropriate
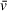
estimate. The Svedberg equation is then used with values either known or input by the user (N , ω, r, ρ,
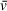
) to solve for particle mass M. The accuracy of molecular weights derived from an SV analysis is therefore dependent on the user-supplied value of
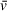
, which is applied to all sedimenting species in a sample in basic analysis approaches. As a result, the
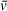
that accurately describes one component of a solution may be significantly different from the
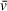
of other solution components, especially in the case of protein-DNA mixtures (i.e., a protein-DNA complex
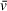
will differ greatly from that of the free DNA or protein). This results in apparent molecular weights for components of heterogeneous solutions that are inaccurate for all or some components, depending on whether the user inputs the theoretical
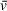
of one component of interest or uses an average of the solution contents weighted by molar ratio. When analyzing SV-AUC data for determination of molecular weight, readers should recognize the potential for errors in user-defined values, such as partial specific volume, to skew results (Demeler et al., 2014). Small errors in
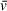
can translate to relatively large differences in calculated molecular weights that do not accurately describe the macromolecules of interest; we highly recommend taking the time to understand the role of partial specific volume in SV analysis calculations.
In experiments using complex solvents (>1 M salt, chaotropic agents, or other components inducing hydrodynamic non-ideality), peak accuracy for apparent molecular weight will be achieved by experimentally determining
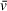
, due to altered contributions from hydration and counterion interactions in these conditions. Densitometers are commercially available for this purpose, but they are not particularly common and require large amounts of sample. Density contrast sedimentation provides a method of experimentally determining
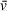
in any solution using AUC, with the inherent benefit (in most cases) of non-destructive experiments (Brown, Balbo, Zhao, Ebel, & Schuck, 2011). This method does, however, require time and expenditure of resources that are likely not reasonable for general AUC use. As a solution to this issue, programs like SEDFIT and UltraScan provide resources to algorithmically determine
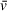
for a given particle with a high degree of accuracy when the solution in question is reasonably close to true aqueous conditions (solvent density <1.002 g/cm3) (Lebowitz, Lewis, & Schuck, 2003). The values predicted by these calculators have proven close to those experimentally determined and, in our hands, have provided satisfactory
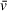
estimates that lead to orthogonally supported molecular weight measurements. SEDFIT and UltraScan also provide methods for fitting
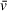
of species in experimental datasets. This is accomplished either by holding f/f0 constant and floating
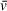
with otherwise the same analysis approach or by assigning multiple
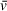
to mixed systems, the latter approach requiring careful user guidance of the modeling process.
Gradient-Forming Species
Given their common use in buffers as a protective agent for proteins and DNA, it is pivotal to account for the solution density contribution of additives such as glycerol or crowding agents. Density gradients will significantly change the interaction of a sedimenting particle with surrounding solution, reducing the apparent sedimentation coefficient (Fig. 1). Small changes in sample viscosity/density can translate to significant sedimentation differences. Co-sedimenting buffer components should be dialyzed out of samples prior to AUC runs wherever possible. In practice, analysis programs such as UltraScan and SEDNTERP can account for the solution density effect of buffer components such as glycerol in solutions, with a recommended upper limit of 5% of these species by weight. In other cases, the inclusion of glycerol may not be a concern, such as when seeking to observe a binding event through shifts in sedimentation coefficient distributions, without concern for quantitative accuracy in sedimentation coefficient (S), diffusion coefficient (D), and apparent molecular weight (M). Values resulting from analysis of such an experiment will not be accurate, but if buffer contents are otherwise identical, a mixture of A and B components that results in sedimentation coefficients larger than A or B alone will still, in general, indicate a binding event.
Detergents and Carrier Proteins
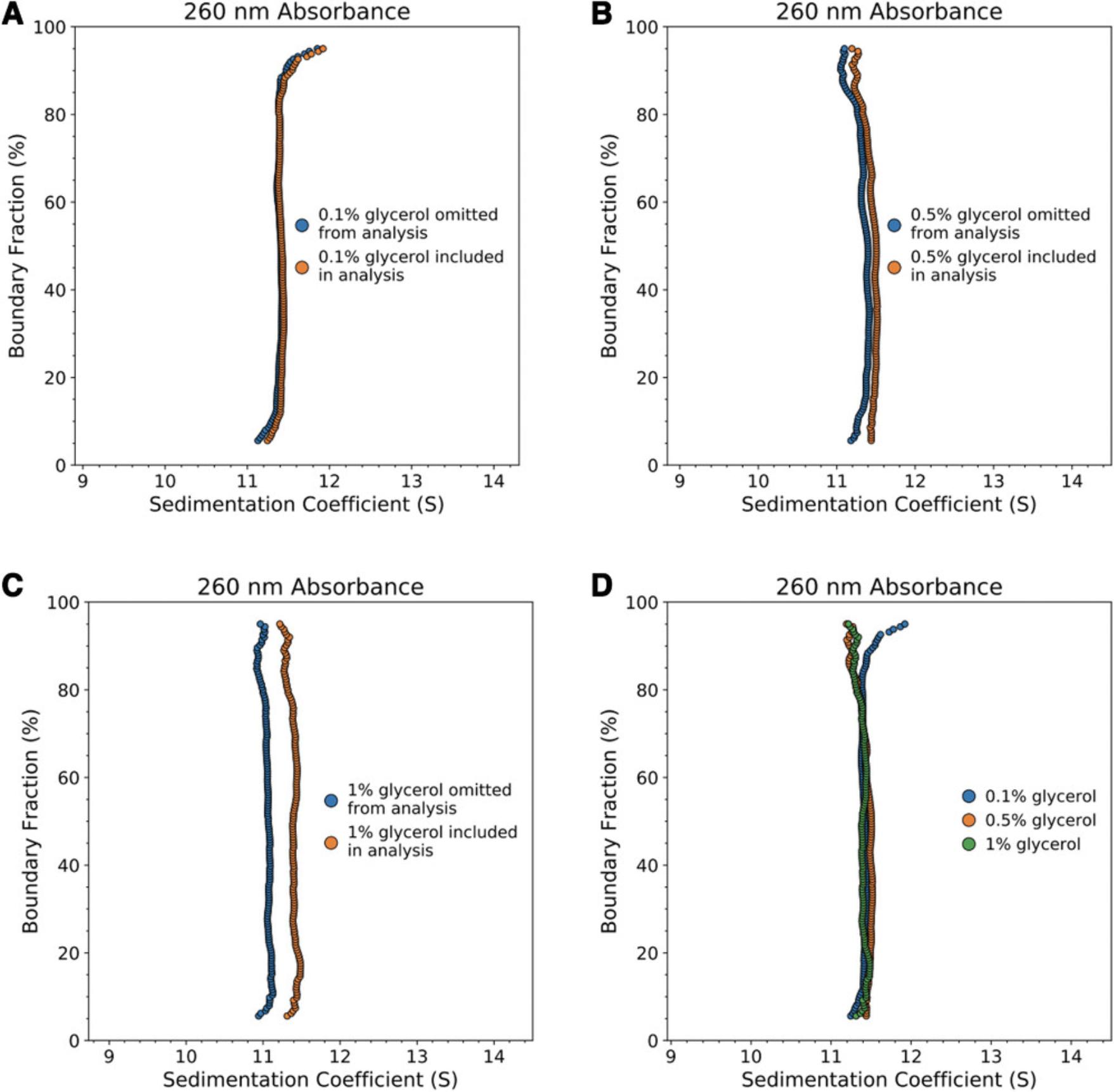
“Sticky” proteins and other macromolecules that adhere to surfaces are problematic for in vitro biological methods. AUC cells, most often composed of a charcoal-epon centerpiece with quartz or sapphire windows, exhibit several solution interface chemistries that might attract particles of interest. An approach that we have found particularly useful to prevent protein adherence to the cell is the inclusion of low concentrations of a detergent such as 3-((3-cholamidopropyl) dimethylammonio)-1-propanesulfonate (CHAPS) or β-D-Octylglucopyranoside [about 0.01% to 0.1% (w/v)] and/or “blocking” agents (carrier proteins) such as bovine serum albumin (BSA), lysozyme, or casein (about 0.01 to 0.1 mg/ml), especially in cases of low sample concentration common to AUC-FDS experiments. Solution density calculators generally do not have data for the density effect of detergents or a means to include the contribution of carrier proteins to solvent density, necessitating control experiments to ensure that the sedimentation and diffusion behavior of macromolecules is not affected. In general, except for a small intrinsic fluorescence signal from BSA, we have observed no effect on sedimentation profiles from inclusion of blocking proteins that do not bind particles of interest, whereas particle solubility and signal intensity are drastically improved. Similarly, the inclusion of detergents at low concentrations (below the critical micelle concentration) has a negligible impact on observed sedimentation and diffusion behavior (Fig. 2A, Table 3) and enables the collection of sedimentation data for samples with solubility problems (Fig. 2B and 2C).
| Spn1 | Spn1 (0.1% CHAPS) | |
|---|---|---|
| S20,W | 2.57 (0.34)a | 2.56 (0.36) |
| f/f0 | 1.99 (0.56) | 2.00 (1.14) |
| M (Da) | 53,107 (31,332) | 52,501 (31,574) |
- a Standard deviations are in parentheses. Peaks were integrated to include all S values observed by vHW.
Fluorescent Labeling of Macromolecules
Fluorophores with 488-nm excitation maxima provide the best signal with current Aviv FDS instruments because this wavelength matches the FDS excitation laser. Dyes with excitation ranges deviating from 488 nm can be used, but they will require higher final concentrations for producing a signal equivalent to that of dyes with maximum excitation at 488 nm. Extrinsic fluorescent labeling of proteins can be accomplished via conjugation of side chains of native amino acids (e.g., carboxylic acids, cysteines) with functionalized fluorophores; however, we find that this often leads to issues with protein folding, functionality, or macromolecular interactions. We have obtained most consistent results from engineered single-site cysteine mutants and labeling with Alexa488-maleimide ester, but this may not be a possibility for many biological systems. When using labeling of native functional groups, or mutation for site-specific labeling, the labeled protein must be rigorously analyzed in biochemical assays to confirm that its behavior is equivalent to that of the native unlabeled protein. Additionally, single-fluorophore labeling on DNA molecules is easily obtained by ordering a conjugated oligo from commercial sources such as IDT or Sigma. Other options include conjugation with fluorescent proteins such as GFP or application of a variety of commercially available reaction chemistries that can be used for single-fluorophore labeling of DNA or proteins. A general discussion of fluorescent labeling of proteins for AUC-FDS was published in 2011 by Jonathan Kingsbury and Thomas Laue (Kingsbury & Laue, 2011).
Pilot Experiments
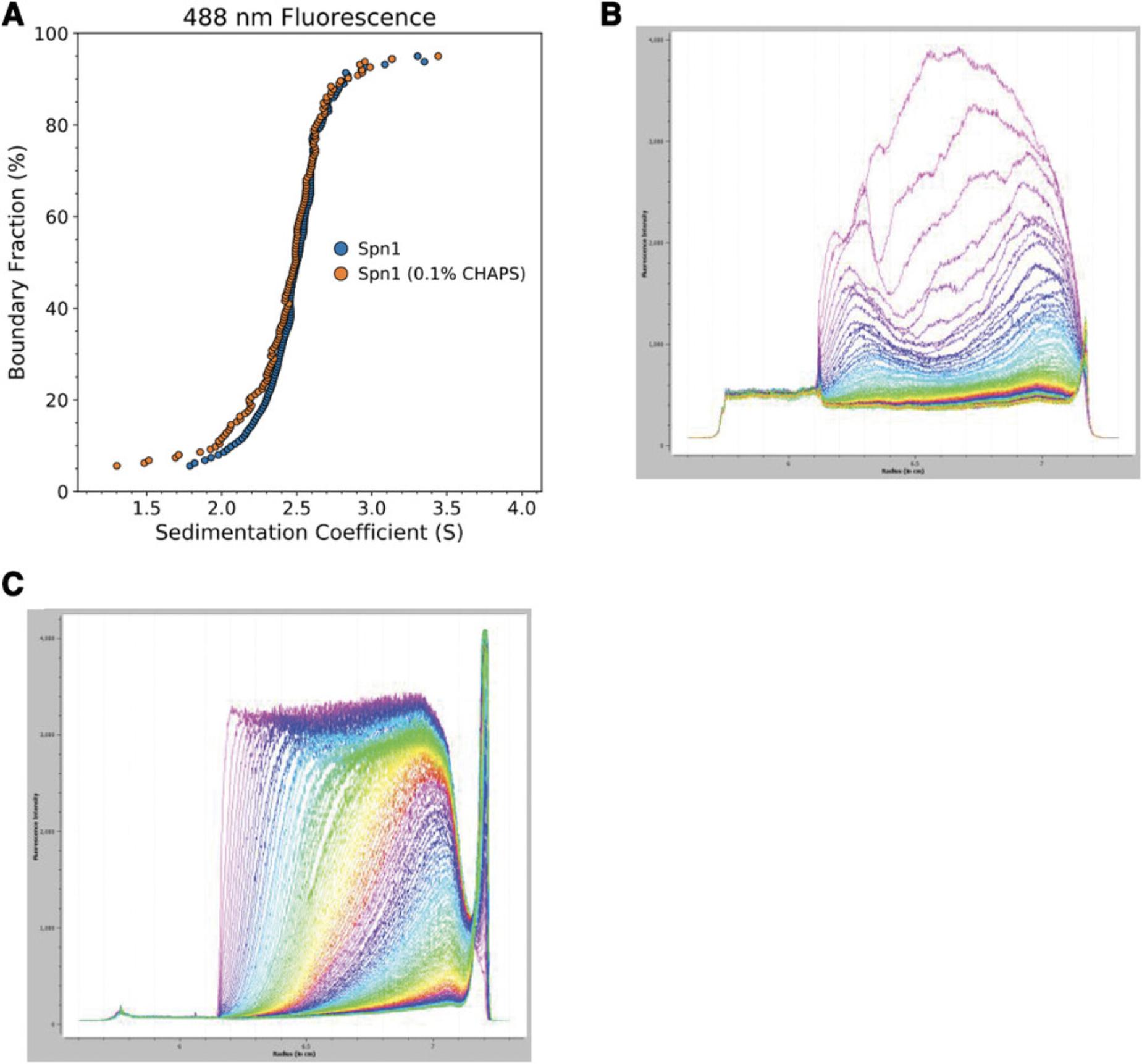
To begin exploring a system of interest by SV-AUC, it is a good idea to start with a pilot experiment. To investigate the properties of single macromolecules, testing for any concentration dependence of sedimentation coefficients (e.g., protein multimerization) in the range of concentrations relevant to the system of interest is an informative control. In mixed systems, an experiment at intermediate speed (roughly the midpoint of ideal speeds for the smallest and largest species’ expected particle sizes) will provide an initial idea of the size and partial concentrations of species in solution. It will also help determine whether speed should be increased or decreased to achieve sufficient resolution of the component of interest. For binding events, a pilot experiment could involve a single sample combining components at the molar ratio of the assumed stoichiometry or may involve several samples with varying concentrations of one or both components to identify the binding event's relevant concentration range and potential stoichiometries. Prior knowledge about the binding interaction from other methods can often inform design and reduce sample requirements for pilot experiments. Figure 3 shows how results from a 280-nm absorbance SV-AUC experiment can be used to design an FDS titration experiment that provides information on complex size, shape, stoichiometry, and rough binding affinity simultaneously, described in more detail below (see “Case Studies”). If very little complex formation is observed with the protein concentrations used in the absorbance experiment in Figure 3, a follow-up experiment might be performed with the same molar ratios but higher total protein concentration or with multiple samples across a range of component concentrations in order to observe complex formation.
Analysis Options
The programs SEDFIT and UltraScan are currently the most widely used for SV analysis. However, we are unaware of any examples in which experimental data were analyzed independently with both methods and the results compared to demonstrate agreement. This can leave users uncertain about the best choice of analysis software. We recommend that users try these and other software packages to identify which best satisfies their needs. To provide a general starting point, we will compare analyses of the same datasets using the primary approaches of each software (see “Basics of SV-AUC Data Analysis in UltraScan and SEDFIT”) to provide some guidance on the strengths of each option relative to the other.
User interface is the most significant difference between the programs. Whereas SEDFIT analyses are conducted fully independently on each sample, UltraScan's default setting requires the importation and categorization of samples according to a collective experiment, rather than an individual sedimentation trace. Additionally, UltraScan requires user input of solution characteristics for each sample (protein/DNA molar ratios and buffer contents of samples, solvent density and viscosity, and individual sample names) prior to any analysis. Although this requires more user time, it also aids in organization and ensures that all analysis results incorporate the UltraScan-predicted (or user-specified)
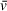
, solvent density, and solvent viscosity values, as well as the most recent stretch calibration of a rotor. In contrast, SEDFIT assumes defaults for all values unless entered after calculation using SEDFIT's Calculator utility and/or an outside resource such as SEDNTERP. Each of these designs has its advantages and drawbacks, and users should decide for themselves what best suits their application.
Another difference between UltraScan and SEDFIT is the focus on model-based versus model-independent approaches. Although the primary modeling approaches implemented by each software utilize the same basic grid search design and are robust, analysis relying on model building is inherently prone to bias and overfitting issues. We have found model-independent analysis to be a valuable tool both for validating model fits and for conducting low-resolution analysis without the need for any modeling. Both programs have utilities built in for model-independent analysis of data by van Holde-Weischet (vHW) transformation; however, this is a more central focus in UltraScan, as reflected in the implementation. UltraScan's “Enhanced van Holde-Weischet” module allows the analysis of full datasets through corrections discussed in its development by Demeler & van Holde (2004). The UltraScan module also provides separate interfaces for a number of functions, including comparison of vHW extrapolations from experimental data to those from models from two-dimensional spectrum analysis (2DSA), removal of scans with optical artifacts (e.g., meniscus not cleared, obstruction of optical path, PMT fluctuation), calculation of weight-averaged sedimentation coefficients for full or partial boundaries, and modulation of back-diffusion tolerance. Conversion of resulting G(s) distributions to more familiar histogram [g(s) or g(s*)] forms is also available in this module. Implementation of vHW analysis in SEDFIT is more limited, as a smaller number of scans that satisfy strict requirements with low optical noise is necessary for generating distributions not dominated by experimental noise. As a result, fewer boundary divisions and only a small subset of scans can be used to produce vHW extrapolations of experimental data in SEDFIT that are not dominated by noise. UltraScan thus provides better functionality for application of model-independent analysis of datasets, which can be crucial for the identification of errors encountered in iterative modeling approaches.
Whereas UltraScan provides an arguably more complete array of model-independent analysis tools, SEDFIT contains increased options for various specific model types and weight-averaged integration of resulting values, as well as a less complicated user experience. Whereas UltraScan's 2DSA always fits peaks in both sedimentation and frictional ratio dimensions, SEDFIT's model selection by the user allows for calculation of sedimentation coefficients or apparent molecular weight distributions with a single f/f0 for all species [continuous c(s) or c(M)], two f/f0 [continuous c(s) with bimodal f/f0], or multiple f/f0 [continuous c(s,f/f0)], the last being analogous to 2DSA and requiring similar computational time on standard desktops. For many applications, such as in an already well-defined two-component system, the less complex modeling approaches will be faster to run and conceptually easier to understand. SEDFIT models can also easily be constrained using prior knowledge about the sample, such as molecular weight, and models are included to test thermodynamic non-ideality, non-interacting discrete species, and other options. Similar constraints are available in UltraScan but require using the more complicated approaches of 2DSA with user-customized fitting grids (2DSA-CG) or discrete model genetic algorithm (DMGA) analysis. Because fitting both sedimentation coefficient and frictional ratio for all peaks is considerably more computationally expensive than fitting one dimension to a common value, SEDFIT may be preferable for analyses that are concerned only with sedimentation or molecular weight distributions and can ignore diffusion/shape information. For such cases, the setup of SEDFIT will be faster and simpler to use.
In both programs, broader applications such as global modeling of multiple datasets, fitting of multi-component reaction parameters, placing a variety of constraints on values such as association constants and stoichiometries, and other options are included; to accomplish these functions, UltraScan requires use of LIMS supercomputing resources, and SEDFIT requires export of results into the extension program SEDPHAT (Demeler, Brookes, & Nagel-Steger, 2009; Zhao, Piszczek, & Schuck, 2015). SV-AUC applications to general biological samples can be rigorously accomplished without these functions, and the advanced analyses are the focus of many publications by the software developers (Brautigam, Padrick, & Schuck, 2013; Brookes & Demeler, 2007; Demeler & Gorbet, 2016; Demeler & van Holde, 2004; Demeler et al., 2009). Functionality is also included in both software packages to generate simulated SV data for ideal particles, which can be parameterized by bead modeling of X-ray crystallography/electron microscopy structures or by using other biophysical data. This can provide a good method to compare both predictions of other techniques and experimental AUC results to idealized, noiseless systems. Another important note is that both software packages are equipped to handle reacting systems with both fast and slow kinetics. Although discrete species or stable/saturated complexes generally result in easier analysis and more precise values, we have found that both UltraScan and SEDFIT handle the situation of mixed systems with complicated reaction boundaries very well (Demeler et al., 2010; Schuck, 2010).
INTERPRETING RESULTS
For researchers unfamiliar with SV-AUC, interpreting results from both model-dependent and model-independent analysis methods may not be intuitive. Conceptually, the most useful terms are those that can be directly measured (s) or modeled (s and f/f0). The frictional ratio is a measure of particle elongation, such that most globular proteins fall between f/f0 values of 1 and 2, whereas most nucleic acids are more rod like and range to values of 4 or above, depending on length and in-solution conformation. Although this ratio cannot distinguish between structures with similar axial ratios, for example, a dumbbell and an ellipsoid of similar dimensions, valuable information on conformational changes induced by folding or binding events can be inferred from the frictional ratio. It is important to understand the relationship of terms in the Svedberg equation in order to interpret SV results, specifically that the sedimentation coefficient of a particle is directly proportional to its mass and inversely proportional to its frictional coefficient (a measure of viscous drag). This relationship means that a particle of a given mass will sediment more slowly (lower sedimentation coefficient) due to viscous drag if its frictional ratio increases, as is seen, for example, in the unfolding of a nucleosome prior to any histone dissociation (see Case Study 3). In rare cases, a large increase in frictional ratio resulting from a binding event can offset the mass increase, such that the sedimentation coefficient is unchanged or even decreases. This is in stark contrast to the general expectation that binding events will result in larger sedimentation coefficients seen in integral or differential sedimentation coefficient distributions. The possibility of counterintuitive results, such as an s decrease with a binding event, emphasizes the value of fitting diffusion/frictional coefficients and of using SV experiments to capture this information. Combining modeling and model-independent analysis methods is a valuable means to validate results, especially when monitoring very small sedimentation shifts. In such cases, and especially in those with small f/f0 changes derived from modeling alone, users should maximize confidence in resulting values by repeating experiments at higher and lower rotor speeds whenever possible.
CASE STUDIES
Due to our greater familiarity with and preference for integral sedimentation coefficient distribution plots [G(s), produced by the vHW analysis method] for display of heterogeneous, multi-sample results, data analysis in the case studies presented below was performed in UltraScan III (v4.0). A comparison of UltraScan results with SEDFIT results is provided in the “Basics of SV-AUC Data Analysis in UltraScan and SEDFIT.” All other modeled values presented were extracted using iterative 2DSA (2DSA-IT) in UltraScan III, with Monte Carlo or genetic algorithm optimization where indicated. vHW analysis was performed in UltraScan III using the “Enhanced van Holde-Weischet” module. Resulting G(s) distributions were overlaid using “Combine Distribution Plots (vHW)” in UltraScan III, and the figures were created using the Matplotlib Python package. Interactive python scripts that readers may utilize to generate plots with a similar aesthetic in their own research are available on the Luger Lab GitHub page: (https://github.com/Luger-Lab/AUC-analysis).
Case Study 1: Determining Size, Shape, and Stoichiometry
Approach
Determination of the mass, general shape, and component makeup of biological macromolecular complexes is key to understanding their function in cells. Absorbance AUC (SV or SE) can be effectively applied for these purposes, but they usually require multiple experiments with several samples at varying rotor speeds due to the signal contribution of unbound components. Characterization of protein complexes by absorbance is also limited in usable concentration range, which is within about 0.1 to 1 OD at a given wavelength. Fluorescence optics allow the use of much lower concentrations and deconvolution of the signal acquired in mixed systems. For example, in the reaction A + B ↔ AB, A can be fluorescently labeled (A*) and saturated with excess B. This results in a sedimentation profile showing only AB and any free A, despite most of the protein in solution being excess free B.
To demonstrate, we have chosen a system of two histone chaperones, Saccharomyces cerevisiae Spn1 and Nap1, that interact with each other, as previously shown by our lab (Li et al., 2018). In the context of a physical interaction influencing regulation at gene promoters, the stoichiometry (and therefore available histone-binding sites) of the Spn1-Nap1 complex is of interest. Nap1 is known to exist in solution in a dimer-tetramer equilibrium, although removal of amino acids 288 to 305 (β-hairpin) eliminates tetramerization without impairing dimerization or in vivo function (Park, McBryant, & Luger, 2008). This Nap1 β-hairpin mutant was studied here to identify a minimal Spn1-Nap1 complex. Spn1 (T185C, mutated for specific attachment of the fluorophore) and Nap1Δ β-hairpin (Nap1Δ βH) constructs were expressed in Escherichia coli , and purified by affinity and size-exclusion chromatography, as described previously (Park et al., 2008; Pujari et al., 2010). Spn1 was labeled with Alexa488 fluorophore (Spn1*). Results from “Enhanced van Holde-Weischet” analysis for each individual protein (Spn1* by fluorescence detection, Nap1Δ βH by absorbance) are shown in Figure 3, indicating homogenous Spn1* monomers and Nap1Δ βH dimers. Of note is the “tail” extending to lower S values observed at the bottom of the boundary fraction of the Nap1Δ βH absorbance AUC sample (Fig. 3A). This is indicative of heterogeneity, often observed in protein samples as a result of either co-purified contaminant proteins or products of degradation of the protein of interest. The effect of contaminants on AUC results is observed by comparing Spn1 + Nap1Δ βH results from absorbance (Fig. 3A) and fluorescence (Fig. 3B) experiments at the same sample concentration. The absorbance experiment (Fig. 3A) indicates a three-state system of Spn1-Nap1 complex (about 5.5 to 6 S), Nap1Δ βH dimer (∼4.8 S), and ∼30% of the boundary in a heterogeneous distribution of free Spn1 and free Nap1Δ βH contaminants. Due to the low (∼0.1 OD 280 nm) signal of the sample as measured by absorbance, the resulting distribution is noisy. In contrast, the sample measured using labeled Spn1 and SV-AUC-FDS at the same protein concentrations as the 280-nm absorbance experiment has a much greater signal-to-noise ratio and appears as a two-state system, as only Spn1* sedimentation is visible (Fig. 3B). This simplifies modeling and increases confidence in resulting values (Table 4). The presence of contaminants in the Nap1Δ βH sample also means that the effective concentration of Nap1Δ βH in solution is lower than estimated by standard methods, impacting quantitative investigation of properties such as binding affinity. The straightforward visualization of contaminant contributions to signal is a general strength of AUC that is lacking in most size-dependent techniques.
| Spn1 (49.13 kDa) | +250 nM Nap1Δ βH | +500 nM Nap1Δ βH | +1 μM Nap1Δ βH | +2 μM Nap1Δ βH | |
|---|---|---|---|---|---|
| S20,W | 2.58 (0.0108)a |
Solute 1 (70%) = 2.62 (0.55) Solute 2 (18.5%) = 5.89 (n/a) |
Solute 1 (43.8%) = 2.63 (0.542) Solute 2 (39.5%) = 5.59 (0.364) |
Solute 1 (32.3%) = 2.605 (0.418) Solute 2 (60.6%) = 5.47 (0.434) |
Solute 1 (12.9%) = 2.42 (0.586) Solute 2 (78.4%) = 5.63 (0.093) |
| f/f0 | 2.01 (0.0523) |
Solute 1 (70%) = 2.14 (0.71) Solute 2 (18.5%) = 2.58 (n/a) |
Solute 1 (43.8%) = 2.38 (1.21) Solute 2 (39.5%) = 2.07 (0.5) |
Solute 1 (32.3%) = 2.1 (1.9) Solute 2 (60.6%) = 2.18 (0.46) |
Solute 1 (12.9%) = 2.17 (0.975) Solute 2 (78.4%) = 1.77 (0.463) |
| M (Da) | 52,640 (2,216) |
Solute 1 (70%) = 61,460 (28,731) Solute 2 (18.5%) = 262,188 (n/a) |
Solute 1 (43.8%) = 67,772 (31,064) Solute 2 (39.5%) = 180,270 (76,092) |
Solute 1 (32.3%) = 58,973 (67,599) Solute 2 (60.6%) = 188,070 (73,371) |
Solute 1 (12.9%) = 61,076 (47,392) Solute 2 (78.4%) = 141,480 (51,794) |
- a Measured solute percentages and fitted-parameter standard deviations are in parentheses. Peaks were integrated to include all S values observed by vHW.
To describe Spn1-Nap1Δ βH complex stoichiometry via molecular weight, samples containing 0.5 µM Spn1* were combined with Nap1Δ βH in a range of concentrations, from 0.25 to 2 µM, and run at 42,000 rpm (Fig. 3B). The [+ 2 µM Nap1Δ βH] sample produced a nearly homogenous complex, which is preferred over more mixed samples (samples containing less Nap1Δ βH) for molecular weight extraction due to the greater resolution provided by more data points for model fitting. Analysis of the data in Figure 3B in UltraScan III yielded the values presented in Table 4, indicating a stoichiometry of 1 Spn1 per 2 Nap1 molecules. This complex has a theoretical molecular weight of 148.18 kDa, compared to the experimentally determined molecular weight of 141.48 kDa (Table 4). f/f0 values for Spn1 and Spn1 + Nap1Δ βH indicate that the complex is more spherical than the elongated Spn1. The observed f/f0 of Spn1, on the high end of the expected range for proteins, reflects what was previously known about Spn1: a central, highly conserved, structured domain is flanked by N- and C-terminal tails that are unstructured and make up about half the total protein mass (Li et al., 2018; Pujari et al., 2010). Analysis of all samples used a common
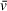
generated by UltraScan for a molar ratio of 1:2 Spn1/Nap1Δ βH. Orthogonal investigation of this system using size-exclusion chromatography with multi-angle light scattering (SEC-MALS) is in close agreement with the complex mass measured here (data not shown).
Given prior knowledge of the mass and sedimentation of complex components and a rough idea of binding affinity, an SV-AUC-FDS experiment at a single sample ratio under saturating binding conditions can yield the same information. However, it is always advisable to perform a titration with both components in excess of binding affinity in order to ensure that the expected A + B ↔ AB scheme is the only binding event occurring under the experimental conditions. Other controls, such as reversing the labeled species and titrant, will further increase confidence in results. Although monomers of A and B proteins are roughly the same size in this example, making the apparent complex weight consistent with several possible stoichiometries, the obligate dimerization behavior of B clearly implies a 1A:2B stoichiometry. In more ambiguous situations, other methods, such as spectral decomposition absorbance AUC, can be employed, especially with the multi-wavelength capabilities of the new Optima AUC (Balbo et al., 2005). For self-associating proteins, UltraScan and SEDFIT include modeling schemes for single-component oligomerization stoichiometry (Gorbet et al., 2014; Zhao et al., 2015).
Alternative approaches
Figure 4 displays the results of absorbance SV-AUC for a multimeric binding interaction (A + B ↔ AB + B ↔ AB2) in which the A component is an 18-bp DNA fragment (11 kDa) and B is the DNA-binding protein PARP1 (115 kDa). Due to the large difference in absorbance of DNA compared to protein at 260 nm, a similar experimental design as described above can be employed, without the need for fluorescence detection. Even with DNA fragments of a much lower mass than that of the binding partner protein, excess protein can generally be used to generate a saturated complex while contributing very little to the total absorbance signal, effectively isolating the sedimentation and diffusion behavior of the complex. 2DSA analysis of the 18-bp DNA + PARP1 sample (1.5 µM DNA, 3.75 µM PARP1) resulted in a modeled molecular weight of 205.52 kDa for the complex (Table 5), reasonably close to the theoretical molecular weight of a DNA-PARP1 complex at a 1:2 stoichiometry (241 kDa). This demonstrates the viability of partial-specific-volume algorithmic predictions using SEDNTERP/SEDFIT/UltraScan, even with mixed systems of complexes of DNA and protein, despite the large differences in
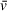
, which is ∼0.55 cm3/g for DNA and ∼0.73 cm3/g for protein in water (Durchschlag, 1989). The modeled values for this system were extracted using a combined
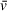
generated from a 1:2 DNA-to-PARP1 complex. Modeled values for the ∼5-S species observable in the vHW plot (presumably free PARP1 and/or 1:1 DNA/PARP1, Fig. 4A) are also reasonably close (i.e., solute 2: 164 kDa modeled, 126 kDa theoretical), but with much larger standard deviations (Table 5). This lack of resolution is related to both the low percentage of the sedimenting boundary occupied by this species and the common
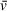
assigned to the sample and used for molecular weight calculation, which does not accurately represent a 1:1 DNA/PARP1 species. For more accurate modeling of the molecular weight of the ∼5-S species, an approach fitting multiple
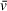
and/or isolating the signal from that complex would be necessary.
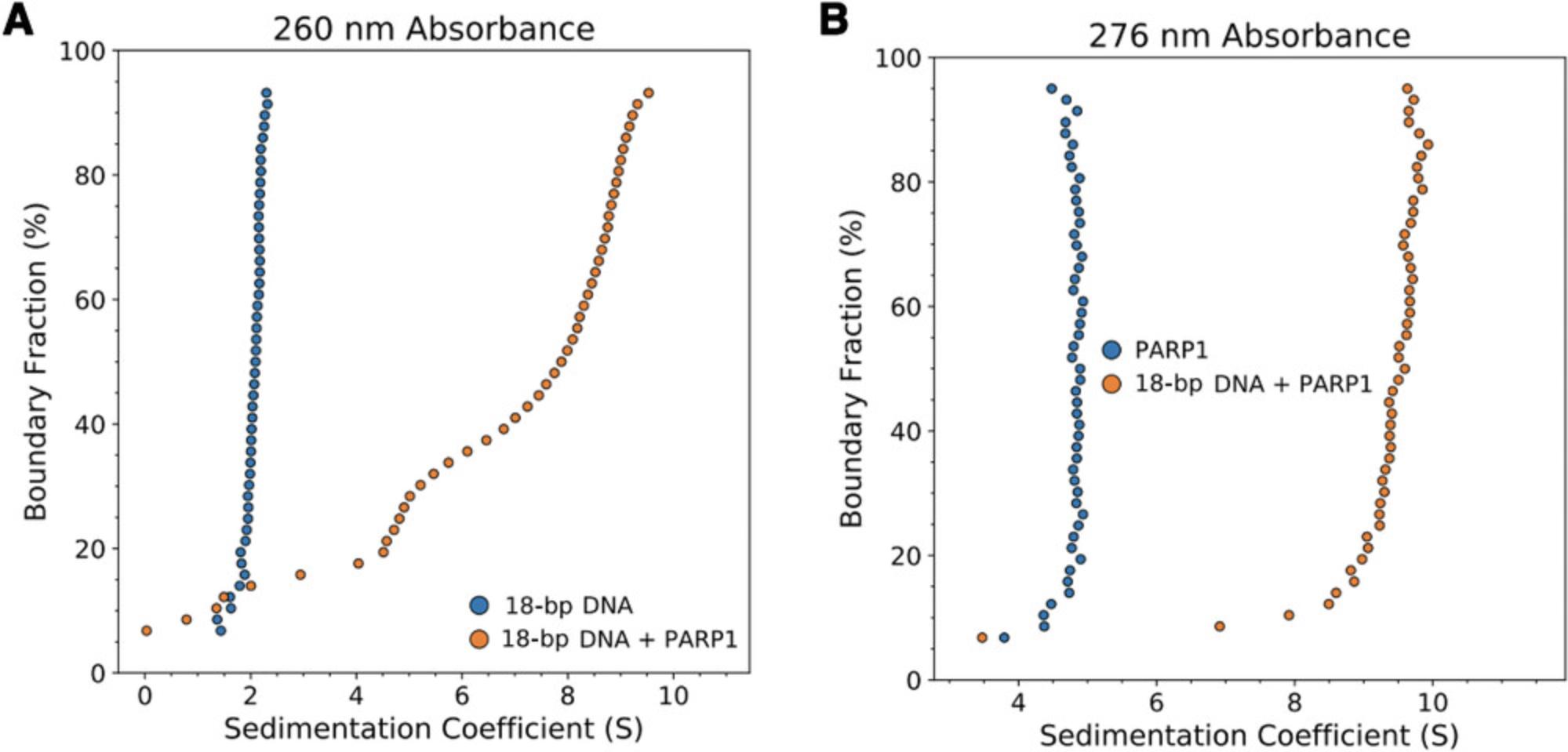
| 260-nm absorbance, 18-bp DNA, theoretical M: 11,003 | 260-nm absorbance, 18-bp DNA + PARP1, Theoretical M of DNA/PARP1: 1:1 = 126,222 Da 1:2 = 241,441 Da | 276-nm absorbance, PARP1, theoretical M: 115,219 | 276-nm absorbance, 18-bp DNA+ PARP1, theoretical M of DNA/PARP1: 1:1 = 126,222 1:2 = 241,441 | |
|---|---|---|---|---|
| S20,W | 2.16 (0.13)a |
Solute 2 (24.22%) 5.02 S (0.965) Solute 3 (58.23%) 9.15 S (0.928) |
4.70 (0.109) | 9.38 (0.84) |
| f/f0 | 1.52 (0.169) |
Solute 2 (24.22%) 2.1 (1.35) Solute 3 (58.23%) 1.36 (0.156) |
1.73 (0.222) | 1.43 (0.63) |
| M (Da) | 11,214 (2,583.4) |
Solute 2 (24.22%) 164,020 (158,080) Solute 3 (58.23%) 205,520 (50,687) |
114,250 (25,781) | 223,210 (19,159) |
- a Measured solute percentages and fitted-parameter standard deviations are in parentheses. The results are from 2DSA-IT analysis with application of Monte Carlo optimization for the 260-nm complex sample. Peaks were integrated to include all S values observed by vHW.
This system was also examined in a 276-nm absorbance experiment. By moving from the 260-nm absorbance peak of DNA, a 276-nm measurement allowed for both a lower concentration to obtain usable signal for PARP1 alone and a higher total concentration of DNA + PARP1 complex (2.5 µM DNA, 2.5 µM PARP1), which increased binding saturation while absorbance measurements remained in the linear range (Fig. 4B). Analysis by 2DSA predicts a molecular weight of 223 kDa for the complex (Table 5), consistent with the idea that the ∼9-S species observed in both experiments is PARP1 bound to 18-bp DNA with a stoichiometry of 1 DNA to 2 PARP1 (241 kDa).
If the initial “guessed” stoichiometry of 1:2 DNA to PARP1 had not been accurate for initial estimation of
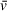
, the resulting mass would likely not have been close to 241 kDa. An apparent molecular weight that does not correspond well to a theoretically possible stoichiometry may indicate an incorrect
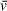
and/or f/f0 estimation, assuming that sedimentation is well resolved. If sedimentation and/or frictional ratio are poorly fit (i.e., not resolved as discrete solute peaks), then apparent molecular weights should only be taken as low-confidence indications, regardless of the accuracy of
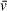
estimation. To help illustrate a first-order approximation of the role of accurate estimations in determining molecular weight, we have developed an open-source and interactive Python script that will recalculate
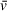
or M estimates using the Svedberg equation and user-provided sedimentation quantities such as buffer density and model-derived values for sedimentation and diffusion coefficients (https://github.com/Luger-Lab/AUC-analysis). With this script, users can explore how even small changes in
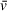
values can have a notable effect on molecular weight estimates; however, this script is intended to provide a simplified example of sedimentation behavior and is entirely dependent on the quality of analysis results and therefore is not a replacement for improved experimental design or orthogonal measurements of
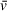
values.
When fitted values are poorly resolved after all available analysis approaches are applied, further experiments are needed to better characterize the system. Higher rotor speed will increase sedimentation resolution, whereas lower rotor speed will improve resolution of diffusion behavior and the frictional ratio. Adjustment of binding component molar ratios and sample buffer conditions can also improve resolution of the fitted parameters, for example, by favoring the formation of a complex of interest. Reducing the complexity of the sedimenting boundary increases both the signal-to-noise ratio and the number of data points available for the complex of interest, improving the ability of analysis methods to identify discrete solutions of the Lamm equation that explain observed sedimentation behavior.
Case Study 2: Measuring Binding Affinities
Approach
The relevance of in vitro quantitation of binding events is dependent on the solution contents in relation to physiological conditions. For this reason, measurements of binding affinity are ideally conducted under conditions that approximate in vivo situations to the highest degree possible. The true solution-state nature of AUC stands out here in that a wide range of buffer conditions can be used, and with an FDS, other components can be included without contribution to optical signal. The ability to directly identify/quantify undesirable events such as aggregation via signal loss is another advantage of AUC over most other methods used to quantitate binding affinity. Although commonly used fluorescence-based binding affinity assays conducted in plate readers [i.e., Förster resonance energy transfer (FRET), fluorescence quenching, fluorescence polarization] will generally require less total protein or DNA sample than SV-AUC-FDS experiments, each suffers from restrictions that do not apply to AUC; for instance, FRET pair proximity, measurable fluorophore quenching/dequenching events, or significant change in anisotropy are required for signal change upon binding in these methods (Pollard, 2010). Fluorescence-based methods also often fail to clearly distinguish aggregation from binding events. Careful experimental design of absorbance/interference AUC experiments can yield association/dissociation constants but requires global fitting of multiple samples and/or experiments, and system applicability is limited because variable binding must be observable within the dynamic range of the detector. Fluorescence-detected SV-AUC provides a conceptually simple and broadly applicable method to study binding events ranging from picomolar to micromolar affinities while requiring only solubility, a sedimentation shift upon binding, and a means to fluorescently tag one component (Zhao et al., 2014). FDS experiments also allow for up to 14 samples to be run simultaneously at the same signal intensity using standard eight-hole rotors and two-channel centerpieces, and sample volume can be reduced to as low as 80 µl without reducing signal or sedimentation column length using 3-mm centerpieces. Three-channel SV centerpieces have been described, indicating the potential for further expanding the number of samples that can be included in an SV-AUC-FDS experiment with the next generation of FDSs (Desai et al., 2016).
To demonstrate the strength of SV-AUC-FDS for binding affinity measurement, we again use the Spn1-Nap1Δ βH system introduced in Case Study 1. Efforts to quantify the binding affinity of this interaction using FRET, fluorescence quenching, and fluorescence polarization all failed due to low observable signal change upon binding. Other indirect methods such as isothermal titration calorimetry (ITC) or surface plasmon resonance could theoretically be used, but SV-AUC-FDS requires less sample, and the components remain free in solution. As a general rule, data points for fitting the dissociation constant (KD) should span from at least 10% to 90% saturation of binding, but wider ranges are preferred where possible. If there is no prior knowledge regarding binding affinity, a pilot SV experiment can be performed with a broad titration to narrow down the concentration range of interest.
Prior knowledge and the experiments performed in Case Study 1 above suggested to us a KD in the low hundreds of nanomolar for this system. The experiments also indicated significant contamination of the Nap1Δ βH protein preparation used and therefore an overestimation of Nap1Δ βH concentration (Fig. 3A). To ensure accurate measurement of binding affinity, a separate Nap1Δ βH preparation without visible contaminants observed by absorbance AUC was used for this assay. A total of 14 samples were prepared containing 10 nM Spn1*, adding Nap1Δ βH to the second through fourteenth samples at concentrations ranging from 5 nM to 10 µM. The experiment was performed at 42,000 rpm. Analysis was performed in UltraScan III with the “Enhanced van Holde-Weischet” module to produce the sedimentation distributions in Figure 5A. In SEDFIT, c(s) analysis of these samples can be used for the same purpose, as described in a related guide (Chaturvedi et al., 2017). Distributions were integrated across the entire boundary to generate weight-averaged sedimentation coefficients, and these values were plotted as a function of Nap1Δ βH concentration and fit with the quadratic solution of the ligand binding equation (Fig. 5B), yielding a KD of 92.1 ± 6.9 nM for this experiment and 100.4 ± 4.5 nM (standard error of the mean) across three experimental replicates.
Alternative approaches for measuring binding affinity and other reaction constants by AUC
Absorbance/interference SV and sedimentation equilibrium (SE) experiments have been used in the past to identify association/dissociation constants, but the applicability of those detection modes to biological binding events is more limited (see Current Protocols article; Demeler, 2010; Laue, 1995; Teller, 1973; Uchiyama et al., 2016). These methods will also require a more detailed global analysis of multiple samples in UltraScan or the SEDFIT extension SEDPHAT (Zhao et al., 2015). The ability to utilize comparably simpler analysis, experimental approaches, and binding-curve fitting methods common to biochemistry research highlights the power of fluorescence-detected SV-AUC experiments for investigating binding interactions.
Case Study 3: Investigation of Macromolecular Assemblies
Approach
The utility of fluorescence-detected AUC is most apparent in its ability to characterize macromolecular complexes with more than two components, which are frequently in a complicated equilibrium between various states. Commonly used biophysical characterization methods that utilize various types of light scattering, as well as absorbance and interference AUC, suffer from reduced resolution when applied to highly heterogeneous samples. With fluorescent tagging, the signal in SV-AUC-FDS is isolated to the sedimentation behavior of a single component in a complex mixture (and the subcomplexes formed by said component), enabling the detailed study of heterogeneous systems.
The eukaryotic nucleosome, composed of four histone heterodimers (two dimers of H2A-H2B flanking an H3-H4 “dimer of dimers”) that are wrapped by a DNA molecule of 147 bp, provides an ideal example test system for this method (Luger, Mäder, Richmond, Sargent, & Richmond, 1997). Solution-state methods such as absorbance AUC, FRET, and small-angle scattering (SAS) have been previously utilized to probe the sensitivity of histone-DNA interactions to ionic strength as a proxy for understanding the folding and unfolding pathways of nucleosomes and chromatin arrays (Abbott, Ivanova, Wang, Bonner, & Ausió, 2001; Böhm et al., 2011; Chen et al., 2017; Gansen et al., 2018; Gautier et al., 2004; Maeshima et al., 2016; Park, Dyer, Tremethick, & Luger, 2004). The approaches used in each of these studies have certain drawbacks. Intra-nucleosomal FRET signal (histone-histone or histone-DNA) is lost at ∼1 M NaCl, and UV absorbance AUC is dominated by the DNA signal and therefore lacks information on the histone content of unfolding nucleosomes. Standard SAS measurements are inherently low resolution and result in a convolution of DNA and protein signals, making it difficult to extract the behavior of individual components without carefully designed contrast variation measurements, which may not be feasible for all systems (Chen et al., 2014). In these cases, the inability to directly monitor histone dissociation leads to different conclusions concerning the precise ionic strength dependence of histone-DNA association (Chen et al., 2017; Gansen et al., 2018).
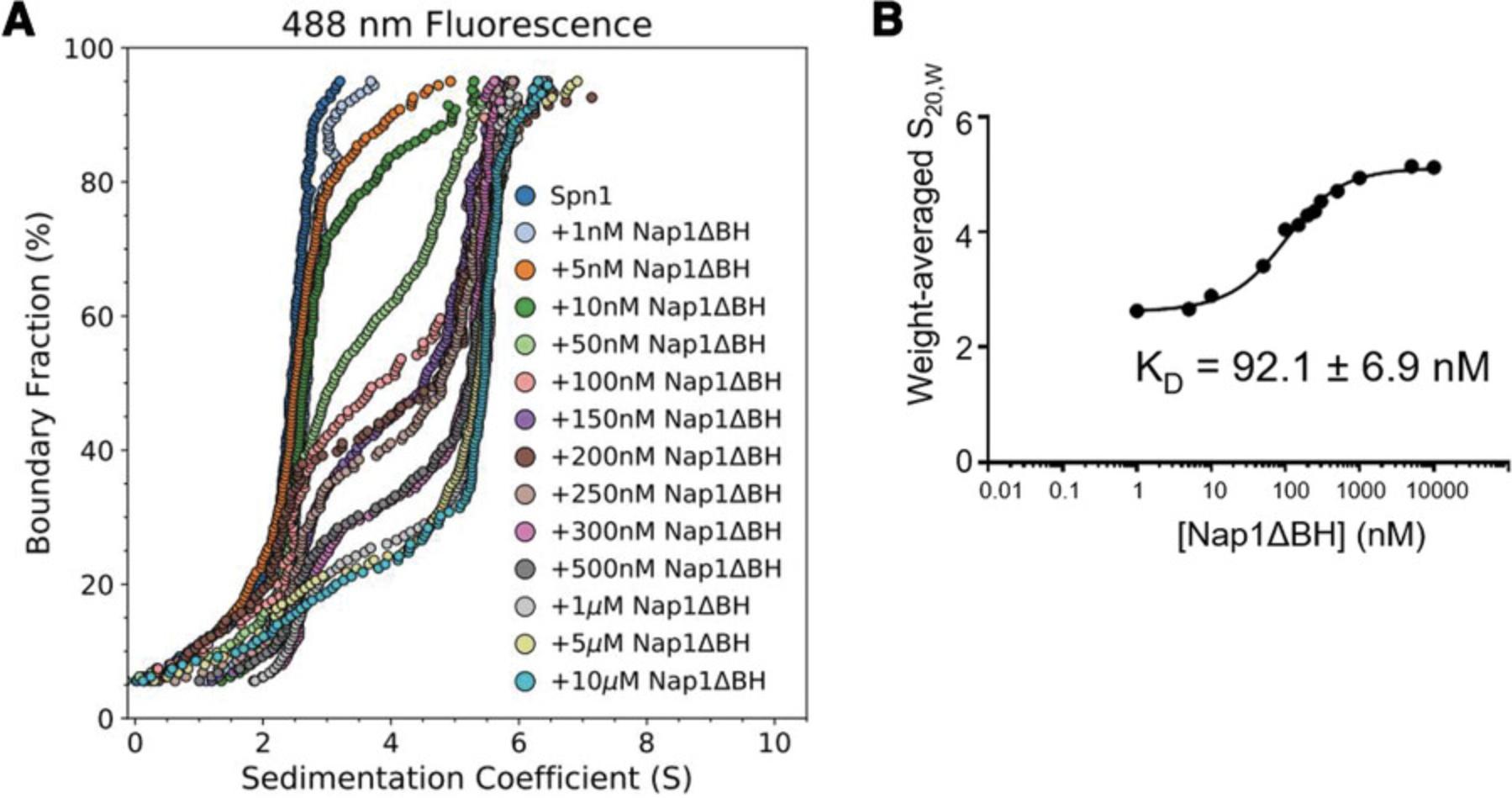
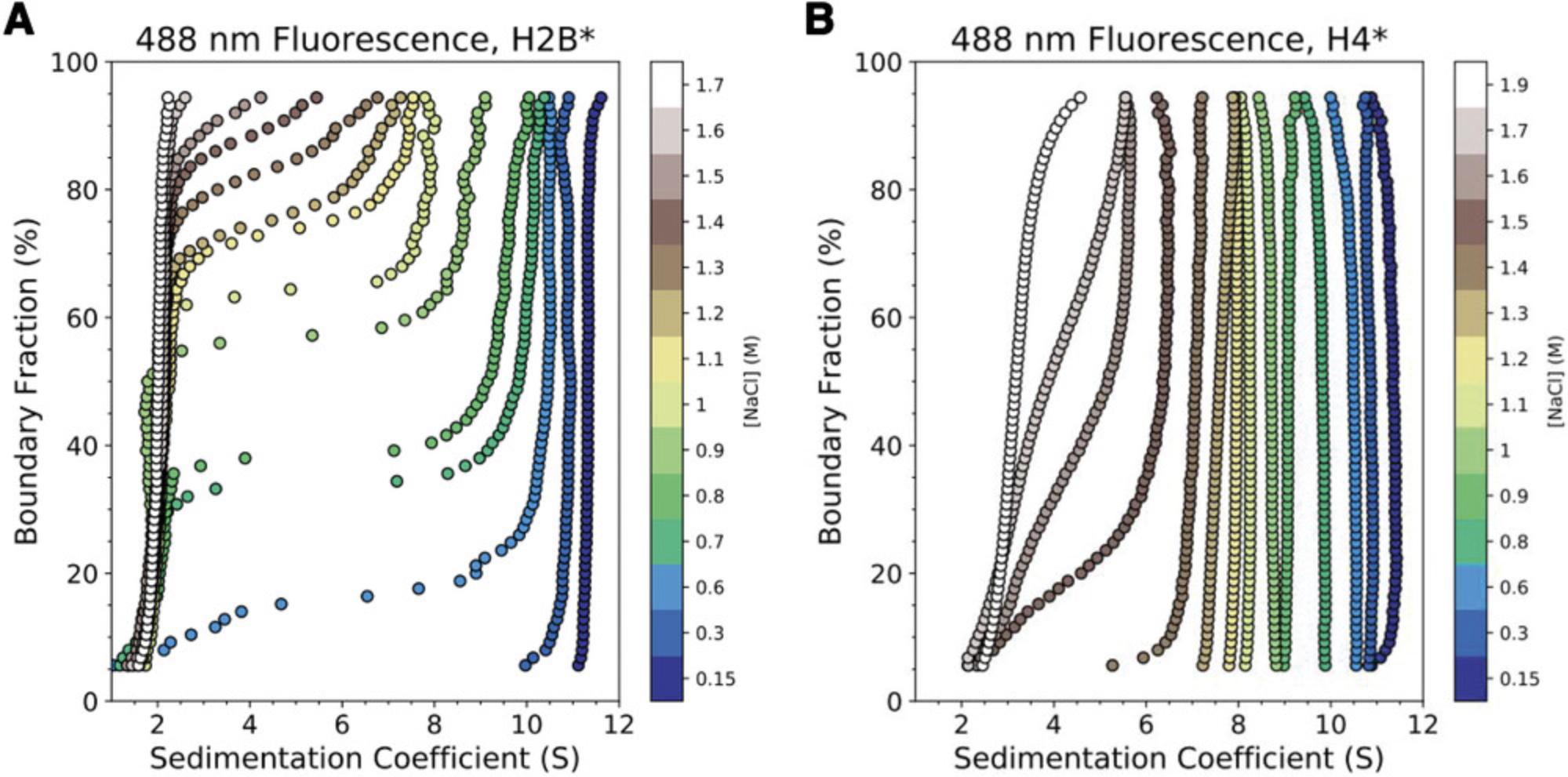
Using single-cysteine mutations of Xenopus laevis histone H2B (T112C) or H4 (E63C), we monitored ionic strength–induced unfolding and histone dissociation of salt-reconstituted X. laevis nucleosomes containing the 147-bp 601-Widom DNA (Dyer et al., 2004). Results are displayed in Figure 6. By including histone cores where either H2B or H4 is fluorescently labeled (H2B*, H4*), the salt-dependent dissociation of H2A-H2B* or H3-H4* heterodimers from the nucleosome can be monitored directly, providing higher resolution of the stepwise nucleosome unfolding process than accomplished by previous approaches (Abbott et al., 2001; Böhm et al., 2011; Chen et al., 2017; Gansen et al., 2018; Gautier et al., 2004; Park et al., 2004). “Enhanced van Holde-Weischet” analysis (Fig. 6) shows that canonical X. laevis nucleosomes “lose” H2A-H2B* dimers between 0.6 and 1.2 M NaCl, with weak associations remaining at >1.2 M NaCl, and that H3-H4* dissociates between 1.4 and 1.9 M NaCl. Figure 7 provides a cartoon schematic depicting this unfolding process and the resulting species in solution. These results agree with observations made by Chen et al. using contrast-variation SAXS (Chen et al., 2017; Chen et al., 2014). 2DSA modeling with genetic algorithm–Monte Carlo (GA-MC) optimization of these results reveals a transition in f/f0 from ∼1.5 to ∼2 between 0.15 and 1.2 M NaCl (Table 6), indicating a significant elongation (or opening) of nucleosome/sub-nucleosome particles. These data may explain the discrepancy between our values and those observed by the Langowski group, as the increase in FRET-pair distance due to nucleosome opening could yield a loss in FRET signal without histones necessarily dissociating from the DNA (Gansen et al., 2018).
| 0.15 M NaCl | 0.3 M NaCl | 0.6 M NaCl | 0.7 M NaCl | 0.8 M NaCl | 0.9 M NaCl | 1 M NaCl | |
|---|---|---|---|---|---|---|---|
| f/f0 | 1.47 (0.004)a | 1.56 (0.005) | 1.64 (0.006) | 1.67 (0.008) | 1.74 (0.005) | 1.79 (0.061) | 1.84 (0.06) |
- a Standard deviations are in parentheses. Values were extracted from 2DSA-IT analysis followed by genetic algorithm–Monte Carlo optimization. Peaks were integrated to include all S values observed by vHW. The observed trend is consistent across three replicates.
Alternate approaches for investigating macromolecular assemblies
Using stepwise dialysis with descending ionic strength (0.1- to 0.3-M salt steps with ≥4 hr of dialysis), an otherwise equivalent experimental design proceeding down an ionic strength gradient (2 M → 0.15 M NaCl) led to the results depicted in Figure 8, confirming the reversibility of the nucleosome folding/unfolding pathway depicted in Figure 7 and observed by other methods (Chen et al., 2017; Gansen et al., 2018). Figure 9 shows the results of a salt-induced nucleosome unfolding experiment conducted without labeled histones and using absorbance (260 nm) SV-AUC, highlighting the dramatic increase in histone dissociation information provided by FDS experiments.
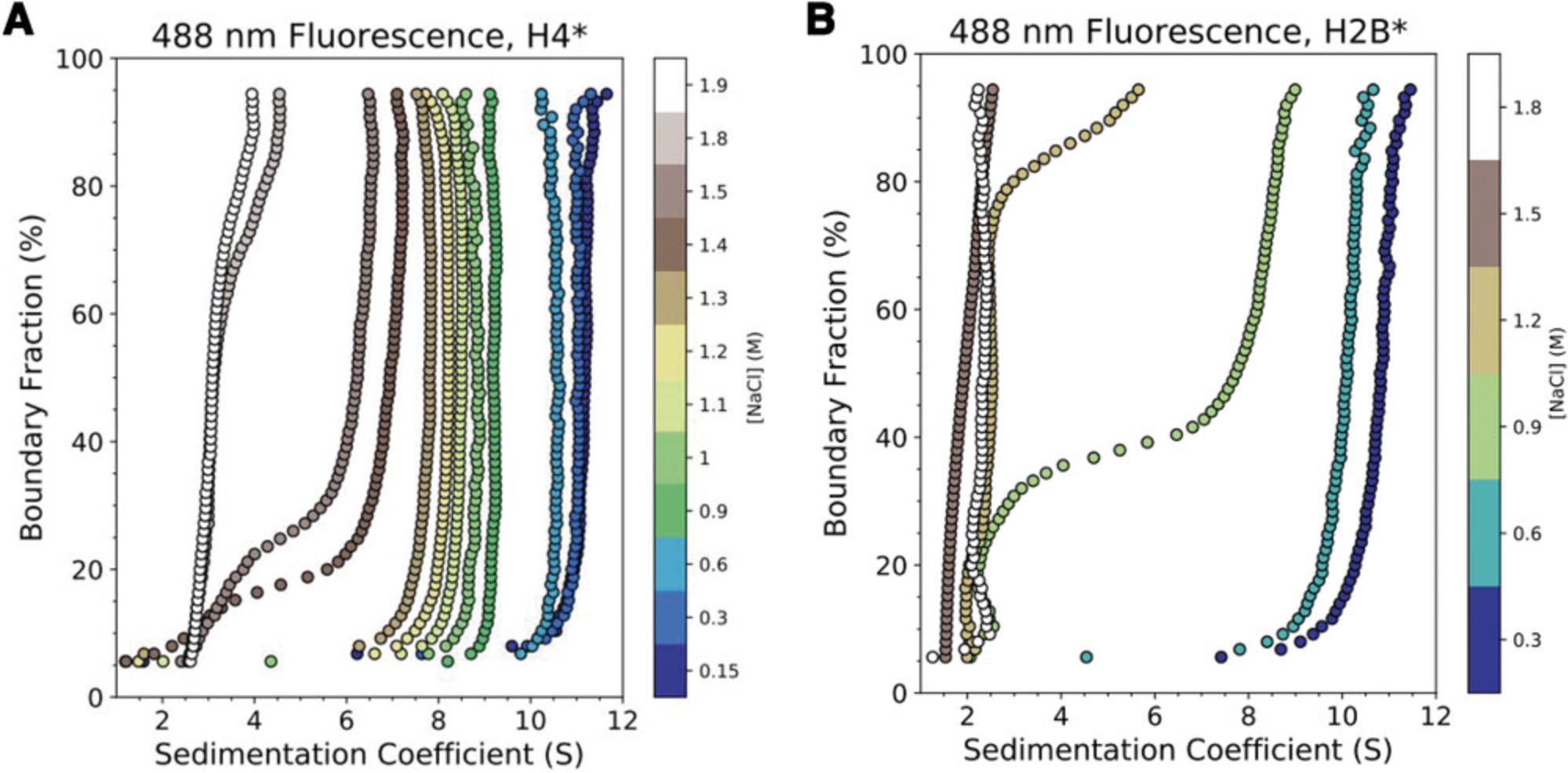
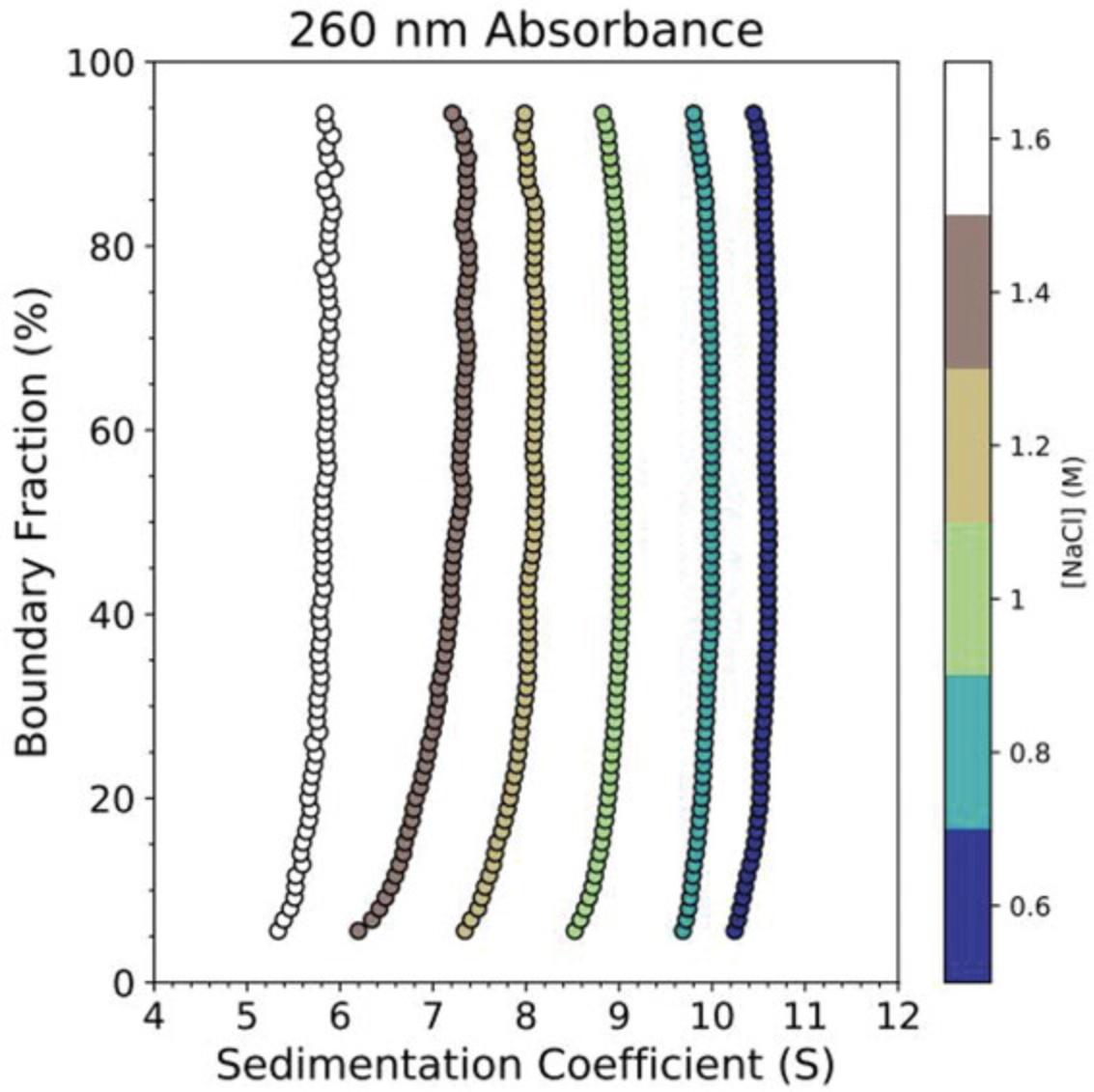
Ionic strength dependence is only one of various approaches that can be used to study multi-component complexes with AUC-FDS. Thermal denaturation is another commonly used assembly/disassembly approach that may be applicable within the temperature range of AUC instruments (Taguchi, Horikoshi, Arimura, & Kurumizaka, 2014). A variety of other experimental designs, such as varying the concentrations of buffer or complex components and interactors, can be used to explore a wide range of macromolecular complexes in solution.
BASICS OF SV-AUC DATA ANALYSIS IN UltraScan AND SEDFIT
To avoid pitfalls inherent to model-based analysis, it is crucial to have at least a basic understanding of the fitting process. Users should apply as little bias to their analyses as possible, especially when lacking experience. As such, we will address relatively basic, core analysis approaches for the popular analysis programs UltraScan and SEDFIT, where potential user bias is limited to data selection, setting of fitting limits, and evaluation of resulting model fits. To demonstrate, we have analyzed absorbance SV data from the system introduced in Case Study 1 (Spn1, Nap1, and Spn1-Nap1 complex) with both UltraScan III v4.0 (revision 5699) and SEDFIT v16.1c. Both are the latest versions that were available during the preparation of this article.
UltraScan and SEDFIT both utilize numerical solutions of the Lamm equation to analyze the entire sedimenting boundary (formed between depleted and concentrated zones) of SV data. Each program also deconvolutes the data from experimental noise. The details of the mathematical approaches used differ somewhat, but the overall result is the same: sequential SV scans are used to fit common solutions of the Lamm equation using a grid search method, with an approach based on a moving frame of reference that accounts for sedimentation of particles toward the bottom of the cell over time. Users select initial positions for the meniscus and cell-bottom positions, define the range of radial positions and scans to analyze, and select fit limits for values such as the sedimentation coefficient (S). Then, an iterative modeling process (with user evaluation and adjustments between steps) is applied to accurately fit meniscus and cell-bottom positions and time-invariant and radially invariant noise contributions in the raw data, resulting in an idealized sedimentation profile for further analysis. Of note, menisci are more difficult to visually identify in fluorescence data than absorbance data, but both analysis programs can reliably fit meniscus position based on the sedimentation profile from a nearby initial guess; methods for direct visualization of the meniscus in FDS sedimentation profiles have also been described (Bailey, Angley, & Perugini, 2009; Zhao et al., 2013). Nonlinear regression for solutions of the Lamm equation that best describe the noise-deconvoluted data is used to generate probability distributions for sedimentation coefficient (S), frictional ratio (f/f0), diffusion coefficient (D), apparent molecular weight (M), and partial concentrations. The rigorous theoretical basis of these approaches is discussed at length elsewhere (Demeler & Saber, 1998; Schuck, 1998).
Basic analysis guides for each software are available, and video walkthrough tutorials can be found for some specific cases (https://SEDFITsedphat.nibib.nih.gov/tools/Tutorials/Forms/AllItems.aspx; https://www.UltraScan3.aucsolutions.com/sed-veloc-flowchart.php). The most direct comparisons can be made between results from SEDFIT using continuous c(s,f/f0) and UltraScan's 2DSA-IT. Table 7 presents a comparison of the two analysis methods with three 280-nm absorbance samples (Spn1, Nap1Δ βH, and Spn1 + Nap1Δ βH) from an SV-AUC experiment, following the general strategy described in the guides above, with a value of 100 for the resolution parameter on final fitting steps. Notably, S, f/f0 , and molecular weight values, as well as standard deviations, were in close agreement between the two programs. Although the standard deviations from this basic level of analysis performed by either software are large relative to the weight-averaged values, this is generally due to false-positive noise peaks and peak splitting in the f/f0 dimension, a characteristic of grid search methods. Further application of global analysis of multiple samples/experiments and/or stochastic search methods can often resolve discrete species with greatly improved confidence statistics that are consistent with the weight-averaged values from integration of multimodal peaks in 2DSA or c(s,f/f0) analysis. Both software packages are equipped with Monte Carlo–based stochastic fitting approaches to improve model resolution.
| S20,W | f/f0 | M (Da) | Theoretical M | |
|---|---|---|---|---|
| Spn1 (2DSA-IT) | 2.67 (0.042)a | 1.91 | 51,494 (8,616.5) | 49,130 (monomer) |
| Spn1 (c(s,f/f0)) | 2.58 (0.254) | 1.87 | 48,068 (12,125) | 49,130 (monomer) |
| Nap1Δ βH (2DSA-IT) | 4.95 (0.082) | 1.67 | 104,590 (14,664) | 99,052 (dimer) |
| Nap1Δ βH (c(s,f/f0)) | 4.84 (0.168) | 1.63 | 100,721 (37,839) | 99,052 (dimer) |
| Spn1 + Nap1Δ βH (2DSA-IT) | 5.93 (0.435) | 1.80 | 150,640 (68,090) | 148,182 (1:2) |
| Spn1 + Nap1Δ βH (c(s,f/f0)) | 5.59 (0.453) | 1.77 | 142,179 (68,900) | 148,182 (1:2) |
- a Standard deviations are in parentheses. Peaks were integrated to include all S values observed by vHW.
To conduct similar analyses, especially on mixed systems, users of either software should take care to avoid setting fit limits too close to peaks being modeled. Divergence to fit limits can, in some cases, result in good models according to the RMSD between the model and experimental radial scans, but these models are, in reality, based on non-physical values. Identification of abnormalities in modeling, as well as in experimental data, is a crucial requirement of the user in order to conduct rigorous model-based SV-AUC analysis. The raw experimental datasets shown in Figure 2, which demonstrate that varying the buffer conditions of a pure protein can result in good (Fig. 2C) and bad (Fig. 2B) data, highlight the need for user curation of what data are to be analyzed (i.e., display a standard sedimentation profile, not one obscured by lack of particle solubility). Any SV analysis software will readily import and attempt to analyze the data in Figure 2C, often coming to a fairly low-RMSD model. However, the computed solutes of such a model will have no relation to the actual sample contents, and visually, the model will not be a good fit to the experimental data. Both UltraScan and SEDFIT validate model fits based on RMSD but also offer visual representations of the fits by overlaying modeled data on experimental data and by graphing the corresponding residuals. Systematic deviation in residuals and divergence of peaks in resulting distributions to the upper and lower fit limits of S and f/f0 are both indicative of poor fits and should be points of emphasis for assessing model quality, rather than relying on RMSD values alone. Without a complete understanding of how model quality should be assessed, low-RMSD results may prompt users to draw conclusions from the distributions, which are not at all representative of the contents of a sample solution.
FINAL CONSIDERATIONS
Case studies and analysis recommendations in this work are presented in a way that is intended to be as generally applicable as possible. Users will need to exercise their own judgment in adjusting these approaches to more closely fit their needs. Our examples of analysis are limited to the basic needs of most users, but for advanced statistical analyses, readers should familiarize themselves with the body of work from the labs developing SEDFIT and UltraScan.
The primary limitations of AUC-FDS are the requirement for fluorescent tags, the limitation of the Aviv FDS to 488-nm laser excitation, and the availability of instrumentation. In special cases, the intrinsic fluorescence of proteins (i.e., BSA) may negate the need for fluorescent tagging, but most will require it. Fortunately, the options for protein and nucleic acid conjugation with fluorophores continue to expand. Fluorescence artifacts such as quenching may occur upon binding of a labeled species, but this can be worked around through experimental design.
Aviv has ceased production of FDSs. Future development of fluorescence systems will be necessary for wider use and further advancement of method capabilities. In particular, the potential for simultaneous multichannel fluorescence excitation opens the door to a variety of exciting applications of this technology for the study of mixed systems of biologically relevant macromolecules.
AUTHOR CONTRIBUTIONS
Garrett B. Edwards : Conceptualization; data curation; formal analysis; investigation; methodology; validation; writing-original draft; writing-review & editing. Uma M. Muthurajan : Data curation; formal analysis; methodology; writing-original draft; writing-review & editing. Samuel Bowerman : Formal analysis; software; validation; writing-review & editing. Karolin Luger : Conceptualization; funding acquisition; project administration; resources; supervision; writing-review & editing.
LITERATURE CITED
- Abbott, D. W., Ivanova, V. S., Wang, X., Bonner, W. M., & Ausió, J. (2001). Characterization of the stability and folding of H2A.Z chromatin particles implications for transcriptional activation. Journal of Biological Chemistry , 276(45), 41945–41949. doi: 10.1074/jbc.M108217200.
- Bailey, M. F., Angley, L. M., & Perugini, M. A. (2009). Methods for sample labeling and meniscus determination in the fluorescence-detected analytical ultracentrifuge. Analytical Biochemistry , 390(2), 218–220. doi: 10.1016/j.ab.2009.03.045.
- Balbo, A., Minor, K. H., Velikovsky, C. A., Mariuzza, R. A., Peterson, C. B., & Schuck, P. (2005). Studying multiprotein complexes by multisignal sedimentation velocity analytical ultracentrifugation. Proceedings of the National Academy of Sciences of the United States of America , 102(1), 81–86. doi: 10.1073/pnas.0408399102.
- Balbo, A., Zhao, H., Brown, P. H., & Schuck, P. (2009). Assembly, loading, and alignment of an analytical ultracentrifuge sample cell. JoVE (Journal of Visualized Experiments) , 33, e1530. doi: 10.3791/1530.
- Böhm, V., Hieb, A. R., Andrews, A. J., Gansen, A., Rocker, A., Tóth, K., … Langowski, J. (2011). Nucleosome accessibility governed by the dimer/tetramer interface. Nucleic Acids Research , 39(8), 3093–3102. doi: 10.1093/nar/gkq1279.
- Brautigam, C. A., Padrick, S. B., & Schuck, P. (2013). Multi-signal sedimentation velocity analysis with mass conservation for determining the stoichiometry of protein complexes. PLOS One , 8(5), e62694. doi: 10.1371/journal.pone.0062694.
- Brookes, E. H., & Demeler, B. (2007). Parsimonious regularization using genetic algorithms applied to the analysis of analytical ultracentrifugation experiments, pp. 361–368. In Proceedings of the 9th Annual Conference on Genetic and Evolutionary Computation. New York: Association for Computing Machinery. doi: 10.1145/1276958.1277035.
- Brown, P. H., Balbo, A., Zhao, H., Ebel, C., & Schuck, P. (2011). Density contrast sedimentation velocity for the determination of protein partial-specific volumes. PLOS One , 6(10), e26221. doi: 10.1371/journal.pone.0026221.
- Brown, P. H., & Schuck, P. (2008). A new adaptive grid-size algorithm for the simulation of sedimentation velocity profiles in analytical ultracentrifugation. Computer Physics Communications , 178(2), 105–120. doi: 10.1016/j.cpc.2007.08.012.
- Chassé, M. H., Muthurajan, U. M., Clark, N. J., Kramer, M. A., Chakravarthy, S., Irving, T., & Luger, K. (2017). Biochemical and biophysical methods for analysis of Poly (ADP-Ribose) Polymerase 1 and its interactions with chromatin. Methods in Molecular Biology , 1608, 231–253. doi: 10.1007/978-1-4939-6993-7_16.
- Chaturvedi, S. K., Ma, J., Zhao, H., & Schuck, P. (2017). Use of fluorescence-detected sedimentation velocity to study high-affinity protein interactions. Nature Protocols , 12(9), 1777–1791. doi: 10.1038/nprot.2017.064.
- Chen, Y., Tokuda, J. M., Topping, T., Meisburger, S. P., Pabit, S. A., Gloss, L. M., & Pollack, L. (2017). Asymmetric unwrapping of nucleosomal DNA propagates asymmetric opening and dissociation of the histone core. Proceedings of the National Academy of Sciences , 114(2), 334–339. doi: 10.1073/pnas.1611118114.
- Chen, Y., Tokuda, J. M., Topping, T., Sutton, J. L., Meisburger, S. P., Pabit, S. A., … Pollack, L. (2014). Revealing transient structures of nucleosomes as DNA unwinds. Nucleic Acids Research , 42(13), 8767–8776. doi: 10.1093/nar/gku562.
- Claverie, J. M., Dreux, H., & Cohen, R. (1975). Sedimentation of generalized systems of interacting particles. I. Solution of systems of complete Lamm equations. Biopolymers: Original Research on Biomolecules , 14(8), 1685–1700. doi: 10.1002/bip.1975.360140811.
- Cole, J. L., Lary, J. W., Moody, T., & Laue, T. M. (2008). Analytical ultracentrifugation: Sedimentation velocity and sedimentation equilibrium. Methods in Cell Biology , 84, 143–179. doi: 10.1016/S0091-679X(07)84006-4.
- Demeler, B. (2010). Methods for the design and analysis of sedimentation velocity and sedimentation equilibrium experiments with proteins. Current Protocols in Protein Science , 60, 7.13.1–7.13.24. doi: 10.1002/0471140864.ps0713s60.
- Demeler, B., Brookes, E., & Nagel-Steger, L. (2009). Analysis of heterogeneity in molecular weight and shape by analytical ultracentrifugation using parallel distributed computing. In M. L. Johnson & L. Brand (Eds.), Methods in enzymology (Vol. 454, pp. 87–113). Cambridge, MA: Academic Press. doi: 10.1016/S0076-6879(08)03804-4.
- Demeler, B., Brookes, E., Wang, R., Schirf, V., & Kim, C. A. (2010). Characterization of reversible associations by sedimentation velocity with UltraScan. Macromolecular Bioscience , 10(7), 775–782. doi: 10.1002/mabi.200900481.
- Demeler, B., & Gorbet, G. E. (2016). Analytical ultracentrifugation data analysis with UltraScan-III. In S. Uchiyama, F. Arisaka, W. F. Stafford, & T. Laue (Eds.), Analytical ultracentrifugation: Instrumentation, software, and applications (pp. 119–143). New York: Springer. doi: 10.1007/978-4-431-55985-6_8.
- Demeler, B., Nguyen, T.-L., Gorbet, G. E., Schirf, V., Brookes, E. H., Mulvaney, P., … Whetten, R. L. (2014). Characterization of size, anisotropy, and density heterogeneity of nanoparticles by sedimentation velocity. Analytical Chemistry , 86(15), 7688–7695. doi: 10.1021/ac501722r.
- Demeler, B., & Saber, H. (1998). Determination of molecular parameters by fitting sedimentation data to finite-element solutions of the Lamm equation. Biophysical Journal , 74(1), 444–454. doi: 10.1016/S0006-3495(98)77802-6.
- Demeler, B., & van Holde, K. E. (2004). Sedimentation velocity analysis of highly heterogeneous systems. Analytical Biochemistry , 335(2), 279–288. doi: 10.1016/j.ab.2004.08.039.
- Desai, A., Krynitsky, J., Pohida, T. J., Zhao, H., & Schuck, P. (2016). 3D-printing for analytical ultracentrifugation. PLOS One , 11(8), e0155201. doi: 10.1371/journal.pone.0155201.
- Durchschlag, H. (1989). Determination of the partial specific volume of conjugated proteins. Colloid and Polymer Science , 267(12), 1139–1150. doi: 10.1007/BF01496937.
- Dyer, P. N., Edayathumangalam, R. S., White, C. L., Bao, Y., Chakravarthy, S., Muthurajan, U. M., & Luger, K. (2004). Reconstitution of nucleosome core particles from recombinant histones and DNA. In C. D. Allis & C. Wu (Eds.), Methods in enzymology (Vol. 375, pp. 23–44). Cambridge, MA: Academic Press. doi: 10.1016/s0076-6879(03)75002-2.
- Faxen, H. (1929). Arkiv. Math. Atron. Fysik 21B, No. 2.
- Gansen, A., Felekyan, S., Kühnemuth, R., Lehmann, K., Tóth, K., Seidel, C. A. M., & Langowski, J. (2018). High precision FRET studies reveal reversible transitions in nucleosomes between microseconds and minutes. Nature Communications , 9(1), 1–13. doi: 10.1038/s41467-018-06758-1.
- Gaullier, G., Roberts, G., Muthurajan, U. M., Bowerman, S., Rudolph, J., Mahadevan, J., … Luger, K. (2019). Bridging of nucleosome-proximal DNA double-strand breaks by PARP2 enhances its interaction with HPF1. bioRxiv , 846618. doi: 10.1101/846618.
- Gautier, T., Abbott, D. W., Molla, A., Verdel, A., Ausio, J., & Dimitrov, S. (2004). Histone variant H2ABbd confers lower stability to the nucleosome. EMBO Reports , 5(7), 715–720. doi: 10.1038/sj.embor.7400182.
- Gorbet, G., Devlin, T., Hernandez Uribe, B. I., Demeler, A. K., Lindsey, Z. L., Ganji, S., … Demeler, B. (2014). A parametrically constrained optimization method for fitting sedimentation velocity experiments. Biophysical Journal , 106(8), 1741–1750. doi: 10.1016/j.bpj.2014.02.022.
- Harding, S. E., & Rowe, A. J. (2010). Insight into protein-protein interactions from analytical ultracentrifugation. Biochemical Society Transactions , 38(4), 901–907. doi: 10.1042/BST0380901.
- Holde, K. E. V., & Weischet, W. O. (1978). Boundary analysis of sedimentation-velocity experiments with monodisperse and paucidisperse solutes. Biopolymers , 17(6), 1387–1403. doi: 10.1002/bip.1978.360170602.
- Hunter, J. D. (2007). Matplotlib: A 2D graphics environment. Computing in Science Engineering , 9(3), 90–95. doi: 10.1109/MCSE.2007.55.
- Juul-Madsen, K., Zhao, H., Vorup-Jensen, T., & Schuck, P. (2019). Efficient data acquisition with three-channel centerpieces in sedimentation velocity. Analytical Biochemistry , 586, 113414. doi: 10.1016/j.ab.2019.113414.
- Kingsbury, J. S., & Laue, T. M. (2011). Fluorescence-detected sedimentation in dilute and highly concentrated solutions. In M. L. Johnson, J. M. Holt, & G. K. Ackers (Eds.), Methods in enzymology (Vol. 492, pp. 283–304). Cambridge, MA: Academic Press. doi: 10.1016/B978-0-12-381268-1.00021-5.
- Lamm, O. (1929). Die differentialgleichung der ultrazentrifugierung. Almqvist & Wiksell.
- Laue, T. M. (1995). Sedimentation equilibrium as thermodynamic tool. In M. L. Johnson & G. K. Ackers (Eds.), Methods in enzymology (Vol. 259, pp. 427–452). Cambridge, MA: Academic Press. doi: 10.1016/0076-6879(95)59055-2.
- Lebowitz, J., Lewis, M. S., & Schuck, P. (2003). Back to the future: A rebuttal to Henryk Eisenberg. Protein Science : A Publication of the Protein Society , 12(11), 2649–2650.
- LeBrun, T., Schuck, P., Wei, R., Yoon, J. S., Dong, X., Morgan, N. Y., … Zhao, H. (2018). A radial calibration window for analytical ultracentrifugation. PLOS One , 13(7), e0201529. doi: 10.1371/journal.pone.0201529.
- Li, S., Almeida, A. R., Radebaugh, C. A., Zhang, L., Chen, X., Huang, L., … Stargell, L. A. (2018). The elongation factor Spn1 is a multi-functional chromatin binding protein. Nucleic Acids Research , 46(5), 2321–2334. doi: 10.1093/nar/gkx1305.
- Luger, K., Mäder, A. W., Richmond, R. K., Sargent, D. F., & Richmond, T. J. (1997). Crystal structure of the nucleosome core particle at 2.8 Å resolution. Nature , 389(6648), 251–260. doi: 10.1038/38444.
- MacGregor, I. K., Anderson, A. L., & Laue, T. M. (2004). Fluorescence detection for the XLI analytical ultracentrifuge. Biophysical Chemistry , 108(1), 165–185. doi: 10.1016/j.bpc.2003.10.018.
- Maeshima, K., Rogge, R., Tamura, S., Joti, Y., Hikima, T., Szerlong, H., … Hansen, J. C. (2016). Nucleosomal arrays self-assemble into supramolecular globular structures lacking 30-nm fibers. The EMBO Journal , 35(10), 1115–1132. doi: 10.15252/embj.201592660.
- Namitz, K. E. W., Tan, S., & Cosgrove, M. S. (2019). Hierarchical assembly of the MLL1 core complex within a biomolecular condensate regulates H3K4 methylation. bioRxiv , 870667. doi: 10.1101/870667.
- Park, Y.-J., Dyer, P. N., Tremethick, D. J., & Luger, K. (2004). A new fluorescence resonance energy transfer approach demonstrates that the histone variant H2AZ stabilizes the histone octamer within the nucleosome. Journal of Biological Chemistry , 279(23), 24274–24282. doi: 10.1074/jbc.M313152200.
- Park, Y.-J., McBryant, S. J., & Luger, K. (2008). A beta-hairpin comprising the nuclear localization sequence sustains the self-associated states of nucleosome assembly protein 1. Journal of Molecular Biology , 375(4), 1076–1085. doi: 10.1016/j.jmb.2007.11.031.
- Philo, J. S. (1997). An improved function for fitting sedimentation velocity data for low-molecular-weight solutes. Biophysical Journal , 72, 435–444. doi: 10.1016/S0006-3495(97)78684-3.
- Philo, J. S. (2006). Improved methods for fitting sedimentation coefficient distributions derived by time-derivative techniques. Analytical Biochemistry , 354, 238–246. doi: 10.1016/j.ab.2006.04.053.
- Pollard, T. D. (2010). A guide to simple and informative binding assays. Molecular Biology of the Cell , 21(23), 4061–4067. doi: 10.1091/mbc.e10-08-0683.
- Pujari, V., Radebaugh, C. A., Chodaparambil, J. V., Muthurajan, U. M., Almeida, A. R., Fischbeck, J. A., … Stargell, L. A. (2010). The transcription factor Spn1 regulates gene expression via a highly conserved novel structural motif. Journal of Molecular Biology , 404(1), 1–15. doi: 10.1016/j.jmb.2010.09.040.
- Rogge, R. A., Kalashnikova, A. A., Muthurajan, U. M., Porter-Goff, M. E., Luger, K., & Hansen, J. C. (2013). Assembly of nucleosomal arrays from recombinant core histones and nucleosome positioning DNA. JoVE (Journal of Visualized Experiments) , 79, 50354. doi: 10.3791/50354.
- Rowe, A. J. (2011). Ultra-weak reversible protein-protein interactions. Methods , 54(1), 157–166. doi: 10.1016/j.ymeth.2011.02.006.
- Schuck, P. (1998). Sedimentation analysis of noninteracting and self-associating solutes using numerical solutions to the Lamm equation. Biophysical Journal , 75(3), 1503–1512. doi: 10.1016/S0006-3495(98)74069-X.
- Schuck, P. (2010). Sedimentation patterns of rapidly reversible protein interactions. Biophysical Journal , 98(9), 2005–2013. doi: 10.1016/j.bpj.2009.12.4336.
- Schuck, P. (2013). Analytical ultracentrifugation as a tool for studying protein interactions. Biophysical Reviews , 5(2), 159–171. doi: 10.1007/s12551-013-0106-2.
- Scott, D. J., Harding, S. E., & Rowe, A. J. (2005). UltraScan—a comprehensive data analysis software package for analytical ultracentrifugation experiments. In Analytical ultracentrifugation: Techniques and methods (pp. 210–230). London: Royal Society of Chemistry. doi: 10.1039/9781847552617-00210.
- Stafford, W. F., III (1992). Boundary analysis in sedimentation transport experiments: A procedure for obtaining sedimentation coefficient distributions using the time derivative of the concentration profile. Analytical Biochemistry , 203, 295–301. doi: 10.1016/0003-2697(92)90316-Y.
- Stafford, W. F., & Sherwood, P. J. (2004). Analysis of heterologous interacting systems by sedimentation velocity: Curve fitting algorithms for estimation of sedimentation coefficients, equilibrium and kinetic constants. Biophysical Chemistry , 108, 231–243. doi: 10.1016/j.bpc.2003.10.028.
- Taguchi, H., Horikoshi, N., Arimura, Y., & Kurumizaka, H. (2014). A method for evaluating nucleosome stability with a protein-binding fluorescent dye. Methods , 70(2–3), 119–126. doi: 10.1016/j.ymeth.2014.08.019.
- Teller, D. C. (1973). Characterization of proteins by sedimentation equilibrium in the analytical ultracentrifuge. In C. H. W. Hirs & S. N. Timasheff (Eds.), Methods in enzymology (Vol. 27, pp. 346–441). Cambridge, MA: Academic Press. doi: 10.1016/S0076-6879(73)27017-9.
- S. Uchiyama, F. Arisaka, W. F. Stafford, & T. M. Laue (Eds.) (2016). Analytical ultracentrifugation: Instrumentation, software, and applications. New York: Springer.
- Wang, T., Liu, Y., Edwards, G., Krzizike, D., Scherman, H., & Luger, K. (2018). The histone chaperone FACT modulates nucleosome structure by tethering its components. Life Science Alliance , 1(4), e201800107. doi: 10.26508/lsa.201800107.
- Zhao, H., Brautigam, C. A., Ghirlando, R., & Schuck, P. (2013). Overview of current methods in sedimentation velocity and sedimentation equilibrium analytical ultracentrifugation. Current Protocols in Protein Science , 71, 20.12.1–20.12.49. doi: 10.1002/0471140864.ps2012s71.
- Zhao, H., Casillas, E., Shroff, H., Patterson, G. H., & Schuck, P. (2013). Tools for the quantitative analysis of sedimentation boundaries detected by fluorescence optical analytical ultracentrifugation. PLOS One , 8(10), e77245. doi: 10.1371/journal.pone.0077245.
- Zhao, H., Ghirlando, R., Alfonso, C., Arisaka, F., Attali, I., Bain, D. L., … Schuck, P. (2015). A multilaboratory comparison of calibration accuracy and the performance of external references in analytical ultracentrifugation. PLOS One , 10(5), e0126420. doi: 10.1371/journal.pone.0126420.
- Zhao, H., Mayer, M. L., & Schuck, P. (2014). Analysis of protein interactions with picomolar binding affinity by fluorescence-detected sedimentation velocity. Analytical Chemistry , 86(6), 3181–3187. doi: 10.1021/ac500093m.
- Zhao, H., Piszczek, G., & Schuck, P. (2015). SEDPHAT – a platform for global ITC analysis and global multi-method analysis of molecular interactions. Methods , 76, 137–148. doi: 10.1016/j.ymeth.2014.11.012.
INTERNET RESOURCES
Luger Lab GitHub page.
SEDFIT download and guide to general use.
UltraScan download and guide to general use.
John Philo's software downloads.
SEDANAL information and download.
Guide to Aviv FDS operation (courtesy of Peter Schuck). Alternatively, search YouTube for “Using the Fluorescence Detector in Sedimentation Velocity Analytical Ultracentrifugation.”
SEDFIT video analysis guide.
UltraScan SV analysis flowchart.
Explanation of why absorbance AUC experiments should be run in intensity mode.
AUC cell centerpiece chemical compatibility guide.
Citing Literature
Number of times cited according to CrossRef: 9
- Vincent Rossi, Sarah E. Nielson, Ariana Ortolano, Isabella Lonardo, Emeline Haroldsen, Drake Comer, Owen M Price, Nathan Wallace, Joan M. Hevel, Oligomerization of protein arginine methyltransferase 1 and its effect on methyltransferase activity and substrate specificity, Protein Science, 10.1002/pro.5118, 33 , 8, (2024).
- Zhen He, Zunhui Ke, Wei Wang, Yahui Liu, Haoran Zhang, Yan Li, Biophysical and Biochemical Characterization of the Binding of the MarR-like Transcriptional Regulator Saro_0803 to the nov1 Promotor and Its Inhibition by Resveratrol, Biomolecules, 10.3390/biom13030541, 13 , 3, (541), (2023).
- Camila Ramos Santos, Clelton Aparecido dos Santos, Evandro Ares de Araujo, Mariana Abrahão Bueno Morais, Maxuel de Oliveira Andrade, Tatiani Brenelli de Lima, Wesley Cardoso Generoso, Mario Tyago Murakami, State-of-the-art experimental and computational approaches to investigate structure, substrate recognition, and catalytic mechanism of enzymes, Polysaccharide-Degrading Biocatalysts, 10.1016/B978-0-323-99986-1.00023-5, (75-107), (2023).
- Jakub Sławski, Joanna Grzyb, Fluorescence-based techniques to assess biomolecular structure and dynamics, Advanced Spectroscopic Methods to Study Biomolecular Structure and Dynamics, 10.1016/B978-0-323-99127-8.00007-6, (37-76), (2023).
- Maria Mathieu‐Gaedke, Alexander Böker, Ulrich Glebe, How to Characterize the Protein Structure and Polymer Conformation in Protein‐Polymer Conjugates – a Perspective, Macromolecular Chemistry and Physics, 10.1002/macp.202200353, 224 , 3, (2023).
- Mengxuan Jia, Jianzhong Wen, Olivier Mozziconacci, Elizabeth Pierson, Native Mass Spectrometry in Drug Discovery and Development, High‐Throughput Mass Spectrometry in Drug Discovery, 10.1002/9781119678496.ch10, (317-346), (2023).
- Kayla A Jara, Nikolaus M Loening, Patrick N Reardon, Zhen Yu, Prajna Woonnimani, Coban Brooks, Cat H Vesely, Elisar J Barbar, Multivalency, autoinhibition, and protein disorder in the regulation of interactions of dynein intermediate chain with dynactin and the nuclear distribution protein, eLife, 10.7554/eLife.80217, 11 , (2022).
- Anja Thalhammer, Nina K. Bröker, Biophysical Approaches for the Characterization of Protein-Metabolite Interactions, Cell-Wide Identification of Metabolite-Protein Interactions, 10.1007/978-1-0716-2624-5_13, (199-229), (2022).
- Yang Liu, Hugo Bisio, Chelsea Marie Toner, Sandra Jeudy, Nadege Philippe, Keda Zhou, Samuel Bowerman, Alison White, Garrett Edwards, Chantal Abergel, Karolin Luger, Virus-encoded histone doublets are essential and form nucleosome-like structures, Cell, 10.1016/j.cell.2021.06.032, 184 , 16, (4237-4250.e19), (2021).

